数据结构—基础知识:哈夫曼树
文章目录
- 数据结构—基础知识:哈夫曼树
- 哈夫曼树的基本概念
- 哈夫曼树的构造算法
- 哈夫曼树的构造过程
- 哈夫曼算法的实现
- 算法:构造哈夫曼树
数据结构—基础知识:哈夫曼树
哈夫曼树的基本概念
哈夫曼(Huffman)树又称最优树,是一类带权路径长度最短的树,在实际中有广泛的用途。哈夫曼树的定义,涉及路径、路径长度、权等概念,下面先给出这些概念的定义,然后再介绍哈夫曼树
- 路径:从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径。
- 路径长度:路径上的分支数目称作路径长度。
- 树的路径长度:从树根到每一结点的路径长度之和。
- 权:赋予某个实体的一个量,是对实体的某个或某些属性的数值化描述。在数据结构中,实体有结点(元素)和边(关系)两大类,所以对应有结点权利边权结点权或边权具体代表什么意义,由具体情况决定。如果在一棵树中的结点上带有权值,则对应的就有带权树等概念。
- 结点的带权路径长度:从该结点到树根之间的路径长度与结点上权的乘积。
- 树的带权路径长度:树中所有叶子结点的带权路径长度之和,通常记作WPL。
- 哈夫曼树:设有m个权值{w1,w2,…wm},可以构造一棵含n个叶子结点的二叉树,每个叶子结点的权为w,则其中带权路径长度WPL最小的一叉树称做最优二叉树或哈夫曼树。
例如,下图中所示的3棵二叉树,都含4个叶子结点a、b、c、d,分别带权7、5、2、4,他们的带权路径长度分别为
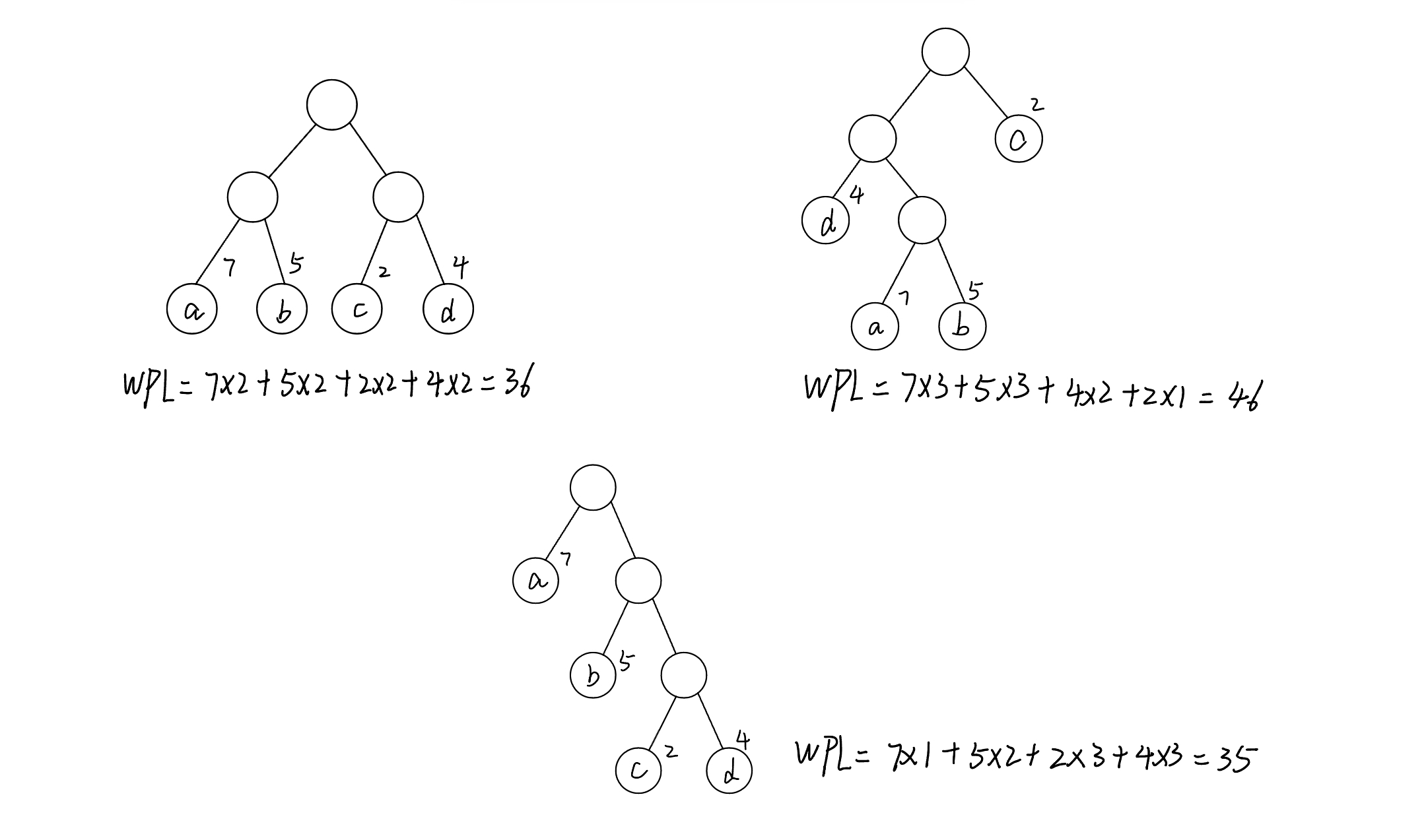
哈夫曼树的构造算法
哈夫曼树的构造过程
- 根据给定的n个权值{w1,w₂,…,wn},构造n棵只有根结点的二叉树,这n棵二叉树构成一个森林F。
- 在森林F中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树,且置新的二叉树的根结点的权值为其左、右子树上根结点的权值之和。(选用两小造新树)
- 在森林F中删除这两棵树,同时将新得到的二叉树加人F中。(删除两小添新人)
- 重复(2)和(3),直到F只含一棵树为止。这棵树便是哈夫曼树。(重复(2)(3)剩单根)
在构造哈夫曼树时,首先选择权小的,这样保证权大的离根较近,这样一来,在计算树的带权路径长度时,自然会得到最小带权路径长度,这种生成算法是一种典型的贪心法。
注:哈夫曼树的结点的度数为0或2,没有度为1的结点。
哈夫曼算法的实现
//-------哈夫曼树的存储表示-------
typedef struct{int weight;//结点的权值int parent,lchild,rchild;//结点的双亲、左孩子、右孩子的下标
}HTNode,*HuffmanTree;//动态分配数组存储哈夫曼树
| 权值 | 双亲 | 左孩子 | 右孩子 |
|---|---|---|---|
| weight | parent | lchild | rchild |
包含n棵树的森林经过n-1次合并才能形成哈夫曼树,共产生n-1个新结点
算法:构造哈夫曼树
【算法步骤】
- 初始化:首先动态申请2n个单元;然后循环 2n-1次,从1号单元开始,依次将1至2n-1所有单元中的双亲、左孩子、右孩子的下标都初始化为0;最后再循环n次,输入前n个单元中叶子结点的权值。
- 创建树:循环n-1次,通过n-1次的选择、删除与合并来创建哈夫曼树。选择是从当前森林中选择双亲为0且权值最小的两个树根结点s1和 s2;删除是指将结点s1 和s2白的双亲改为非 0;合并就是将s1 和 s2的权值和作为一个新结点的权值依次存入到数组的第n+1之后的单元中,同时记录这个新结点左孩子的下标为s1,右孩子的下标为 s2。
void CreateHuffmanTree(HuffmanTree &HT,int n)
{if(n<=1) return;m=2*n-1;HT=new HTNode[m+1];//0号单元未用,所以需要动态分配m+1个单元,HT[m]表示根结点for(i=1;i<=m,++1)//将1~m号单元中的双亲、左孩子,右孩子的下标都初始化为0{HT[i].parnt=0;HT[i].lchild=0;HT[i].rchild=0;}for(i=1;i<=n,++1)//输入前n个单元中叶子结点的权值cin>>HT[i].weight;
/*-----------初始化工作结束,下面开始创建哈夫曼树-----------*/for(i=n+1;i<=n;++1){//通过n-1次的选择、删除、合并来创建哈夫曼树Select(HT,i-1,s1,s2);//在HT[k](1≤k≤i-1)中选择两个其双亲域0且权值最小的结点,并返回它们在HT中的序号s1和s2(最小结点下标)HT[s1].parent=i;HT[s2].parent=i;//修改HT[s1][s2]的parent值HT[i].lchild=s1;HT[i].rchild=s2;//s1,s2分别作为i的左右孩子HT[i].weight=HT[s1].weight+HT[s2].weight;//i的权值为左右孩子之和}
}
已知w=(5,29,7,8,14,23,3,11),构造一棵哈夫曼树,计算树的带权路径长度,并给出构造过程中存储结构HT的初始状态和终结状态。
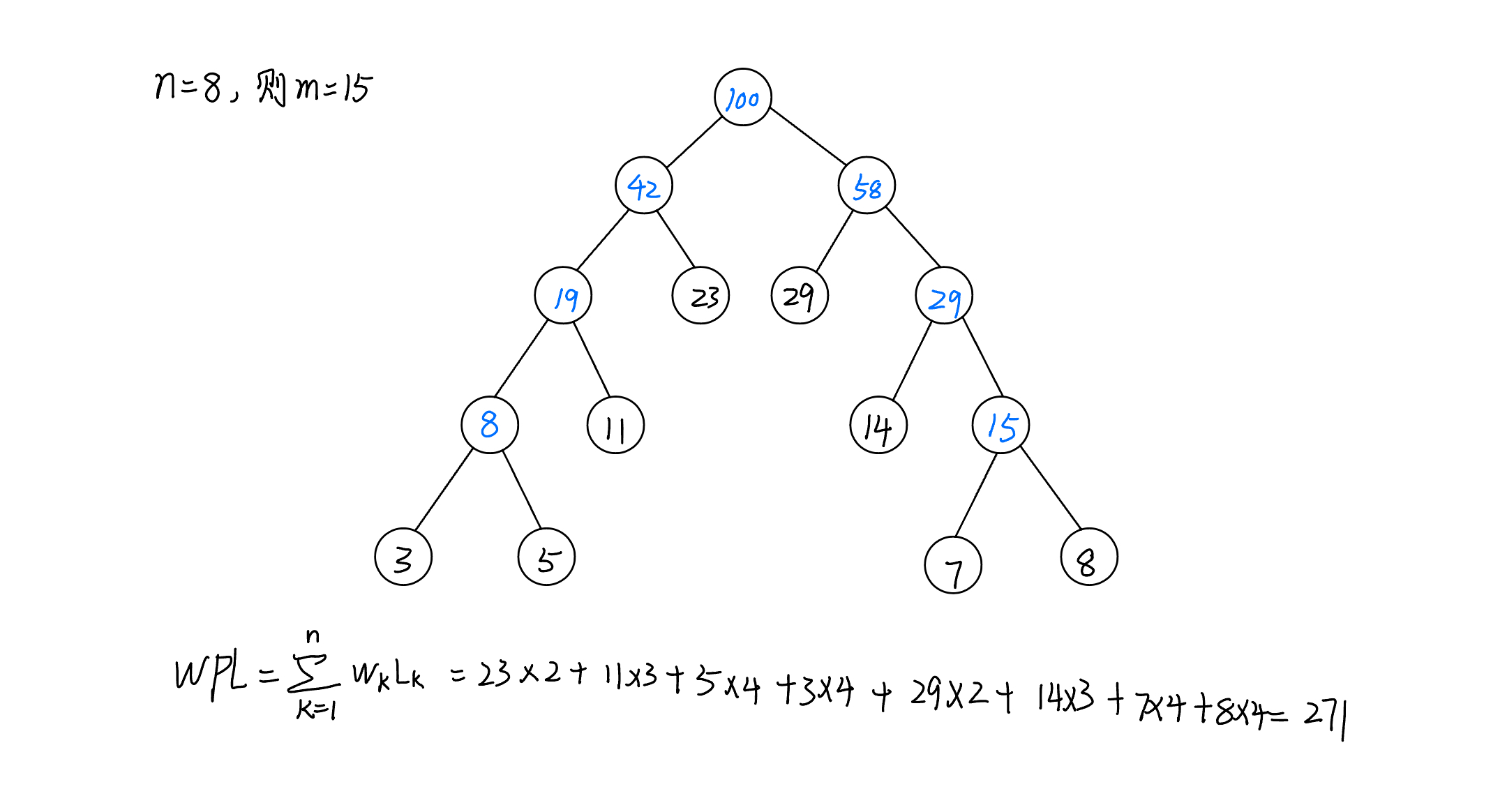
| HT初态 | ||||
|---|---|---|---|---|
| 结点i | weight | parent | lchild | rchild |
| 1 | 5 | 0 | 0 | 0 |
| 2 | 29 | 0 | 0 | 0 |
| 3 | 7 | 0 | 0 | 0 |
| 4 | 8 | 0 | 0 | 0 |
| 5 | 14 | 0 | 0 | 0 |
| 6 | 23 | 0 | 0 | 0 |
| 7 | 3 | 0 | 0 | 0 |
| 8 | 11 | 0 | 0 | 0 |
| 9 | - | 0 | 0 | 0 |
| 10 | - | 0 | 0 | 0 |
| 11 | - | 0 | 0 | 0 |
| 12 | - | 0 | 0 | 0 |
| 13 | - | 0 | 0 | 0 |
| 14 | - | 0 | 0 | 0 |
| 15 | - | 0 | 0 | 0 |
| HT的终态 | ||||
|---|---|---|---|---|
| 结点i | weight | parent | lchild | rchild |
| 1 | 5 | 9 | 0 | 0 |
| 2 | 29 | 14 | 0 | 0 |
| 3 | 7 | 10 | 0 | 0 |
| 4 | 8 | 10 | 0 | 0 |
| 5 | 14 | 12 | 0 | 0 |
| 6 | 23 | 13 | 0 | 0 |
| 7 | 3 | 9 | 0 | 0 |
| 8 | 11 | 11 | 0 | 0 |
| 9 | 8 | 11 | 7 | 1 |
| 10 | 15 | 12 | 3 | 4 |
| 11 | 19 | 13 | 9 | 8 |
| 12 | 29 | 14 | 5 | 10 |
| 13 | 42 | 15 | 11 | 6 |
| 14 | 58 | 15 | 2 | 12 |
| 15 | 100 | 0 | 13 | 14 |
相关文章:

数据结构—基础知识:哈夫曼树
文章目录 数据结构—基础知识:哈夫曼树哈夫曼树的基本概念哈夫曼树的构造算法哈夫曼树的构造过程哈夫曼算法的实现算法:构造哈夫曼树 数据结构—基础知识:哈夫曼树 哈夫曼树的基本概念 哈夫曼(Huffman)树又称最优树&…...
复习提纲24)
计算机网络(第六版)复习提纲24
3 传输控制协议TCP概述 A TCP最主要的特点 1 面向连接的传输层协议 2 每一条TCP连接只能有两个端点,且只能是点对点的 3 提供可靠交付的服务(无差错、不丢失、不重复、不乱序) 4 全双工通信,两端设有发送缓存和接收缓存 5 面向字节…...

[机器学习]TF-IDF算法
一.TF-IDF算法概述 什么是TF-IDF? 词频-逆文档频率(Term Frequency-Inverse Document Frequency,TF-IDF)是一种常用于文本处理的统计方法,可以评估一个单词在一份文档中的重要程度。简单来说就是可以用于文档关键词的提…...

Loadbalancer如何优雅分担服务负荷
欢迎来到我的博客,代码的世界里,每一行都是一个故事 Loadbalancer如何优雅分担服务负荷 前言Loadbalancer基础:数字世界的分配大师1. 分发请求:2. 健康检查:3. 会话保持:4. 可伸缩性:5. 负载均衡…...
计算机网络——链路层(1)
计算机网络——链路层(1) 小程一言专栏链接: [link](http://t.csdnimg.cn/ZUTXU)前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家, [跳转到网站](https://www.captainbed.…...
OpenCV 0 - VS2019配置OpenCV
1 配置好环境变量 根据自己的opencv的安装目录配置 2 新建一个空项目 3 打开 视图->工具栏->属性管理器 4 添加新项目属性表 右键项目名(我这是opencvdemo)添加新项目属性表,如果有配置好了的属性表选添加现有属性表 5 双击选中Debug|x64的刚添加的属性表 6 (重点)添…...

eCos flash模拟EEPROM实现NV系统
Flash需要擦除的原因:先擦除后写入的原因是为了工业上制作方便,即物理实现方便。 #include <cyg/infra/diag.h> #include <cyg/io/flash.h> #include <stdarg.h> #include <stdio.h> #include <stdlib.h> // SPI flash…...

【MongoDB】跨库跨表查询(python版)
MongoDB跨表跨库查询 1.数据准备:2.跨集合查询3.跨库查询应该怎么做? 讲一个简单的例子,python连接mongodb做跨表跨库查询的正确姿势 1.数据准备: use order_db; db.createCollection("orders"); db.orders.insertMan…...
Ruoyi-Cloud-Plus_Nacos配置服务漏洞CVE-2021-29441_官方解决方法以及_修改源码解决---SpringCloud工作笔记199
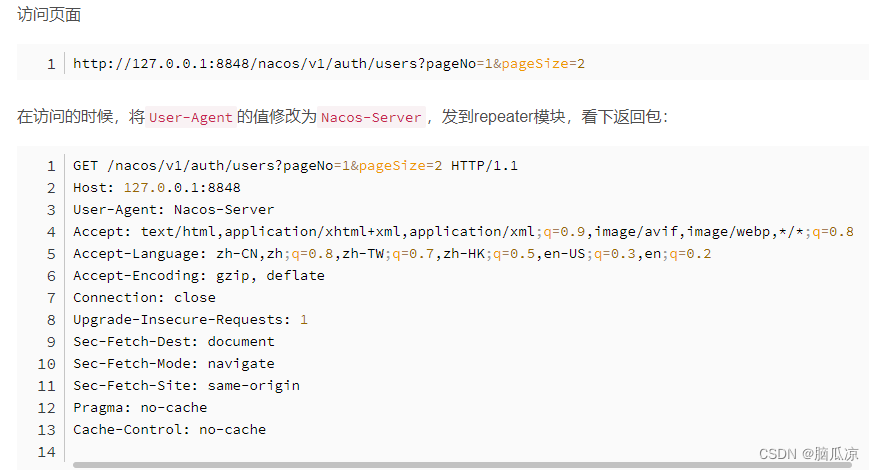
CVE-2021-29441 这个漏洞是Nacos的,通过使用postman,直接访问接口: 就可以直接添加nacos的用户 Nacos是Alibaba的一个动态服务发现、配置和服务管理平台。攻击者通过添加Nacos-Server的User-Agent头部将可绕过(nacos.core.auth.enabled=true)鉴权认证,从而进行API操作。 …...
和鲸科技与智谱AI达成合作,共建大模型生态基座
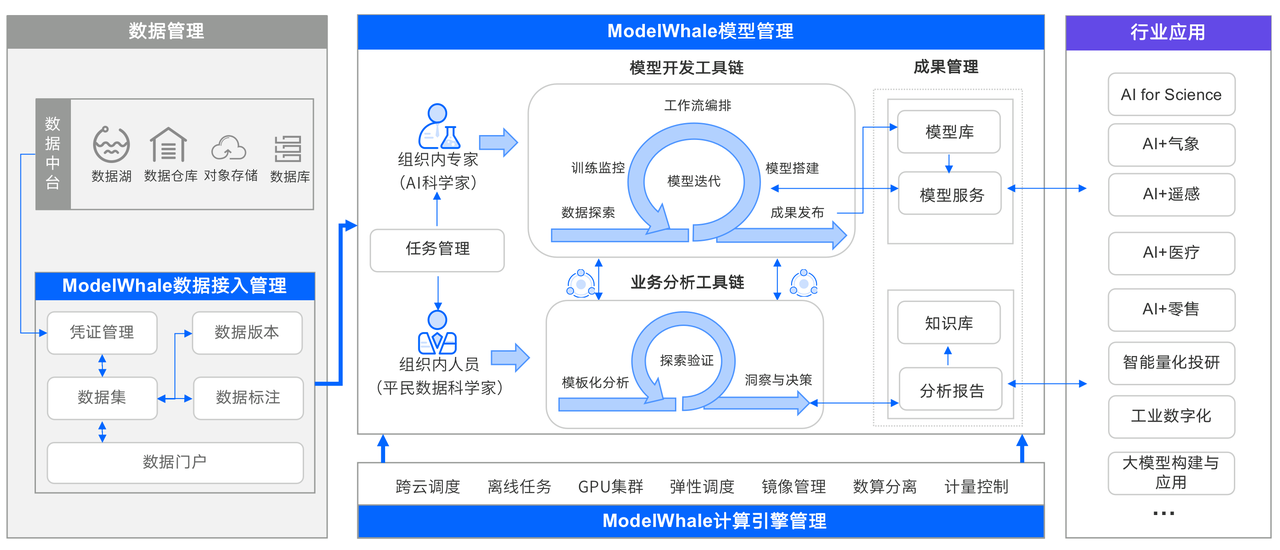
近日,上海和今信息科技有限公司(简称“和鲸科技”)与北京智谱华章科技有限公司(简称“智谱AI”)签订合作协议,双方将携手推动国产通用大模型的广泛应用与行业渗透,并积极赋能行业伙伴探索领域大…...
计算机网络实验五
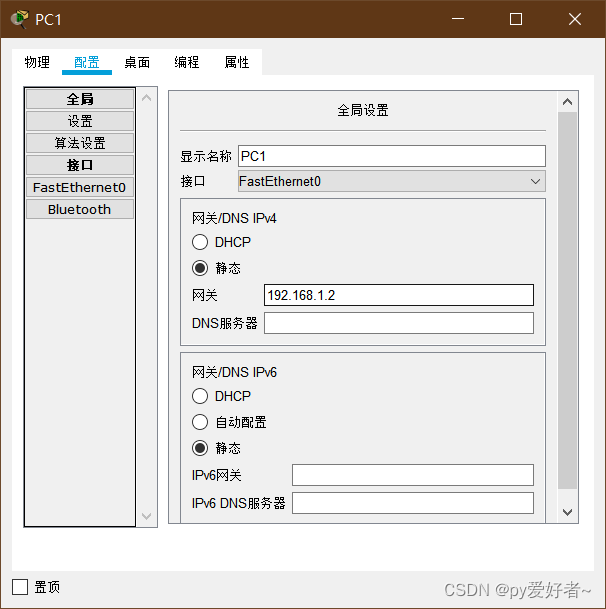
目录 实验五 路由器基本配置 1、实验目的 2、实验设备 3、网络拓扑及IP地址分配 4、实验过程 (1)路由器设备名称的配置 (2)路由器每日提示信息配置 (3)路由器端口的IP地址配置 (4&…...

通过 React 来构建界面
1- 通过 React 来构建界面 第1步:下载所需要的二个库文件至本地,如果需要加载指定版本的 react 和 react-dom,可以把 18 替换成所需加载的版本号。 react.js:React中的核心库文件。 // 开发版 https://unpkg.com/react18/umd/rea…...

真机调试,微信小程序,uniapp项目在微信开发者工具中真机调试,手机和电脑要连同一个wifi,先清空缓存,页面从登录页进入,再点真机调试,这样就不会报错了
微信小程序如何本地进行真机调试?_unity生成的微信小程序怎么在电脑上真机测试-CSDN博客 微信小程序 真机调试 注意事项 uniapp项目在微信开发者工具中真机调试,手机和电脑要连同一个wifi,先清空缓存,页面从登录页进入…...

vue3快速入门
文章目录 1. Vue3简介1.1. 性能的提升1.2.源码的升级1.3. 拥抱TypeScript1.4. 新的特性 2. 创建Vue3工程2.1. 基于 vue-cli 创建2.2. 基于 vite 创建(推荐)vite介绍创建步骤项目结构安装插件项目结构总结 2.3. 一个简单的效果Person.vueApp.vue 3. Vue3核…...
)
go 问题记录(日志丢失)
问题描述: 在go程序中,通过执行一个命令启动一个子命令,并通过pipe读取子程序的标准输入和输出,通过scanner默认按行读取,此时如果子程序输出时没有携带’\n’,scanner就不会打印输出,而是会累…...
彻底解决 MAC Android Studio gradle async 时出现 “connect timed out“ 问题
最近在编译一个比较老的项目,git clone 之后使用 async 之后出现一下现象: 首先确定是我网络本身是没有问题的,尝试几次重新 async 之后还是出现问题,网上找了一些方法解决了本问题,以此来记录一下问题是如何解决的。 …...

计算机网络第4章(网络层)
4.1、网络层概述 简介 网络层的主要任务是实现网络互连,进而实现数据包在各网络之间的传输 这些异构型网络N1~N7如果只是需要各自内部通信,他们只要实现各自的物理层和数据链路层即可 但是如果要将这些异构型网络互连起来,形成一个更大的互…...

SpringbootWeb案例
准备工作 需求说明 部门管理 部门管理功能开发包括:查询部门列表、删除部门、新增部门、修改部门 员工管理功能开发包括:查询员工列表(分页、条件)、删除员工、新增员工、修改员工 环境搭建 环境搭建步骤:1. 准备数据库表(dept、emp)…...
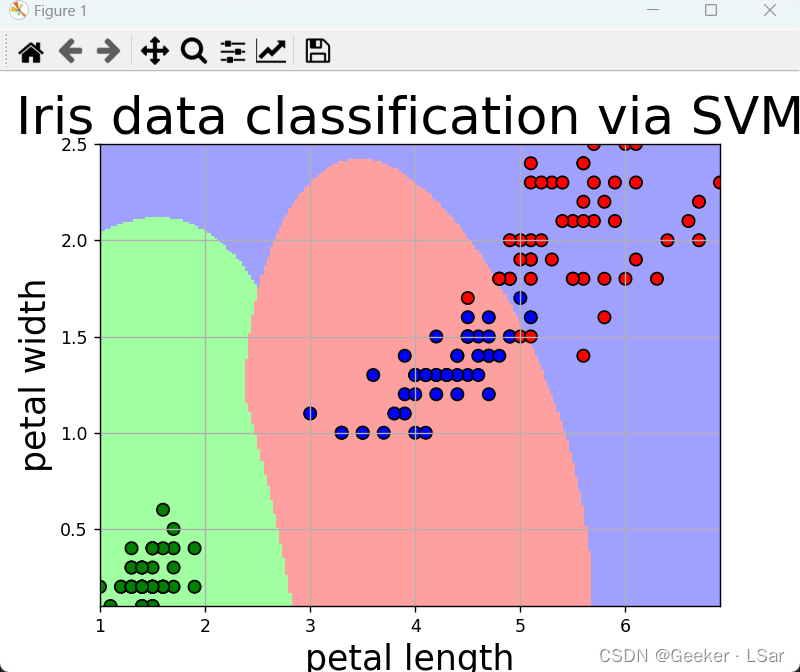
【初中生讲机器学习】4. 支持向量机算法怎么用?一个实例带你看懂!
创建时间:2024-02-02 最后编辑时间:2024-02-03 作者:Geeker_LStar 你好呀~这里是 Geeker_LStar 的人工智能学习专栏,很高兴遇见你~ 我是 Geeker_LStar,一名初三学生,热爱计算机和数学,我们一起加…...
CentOS下安装vlc
一、引言 vlc是一跨多媒体播放器,可以播放本地媒体文件和网络串流,帮助我们排查音视频开发过程中遇到的问题。大部分情况下,我们只需要在Windows系统下安装vlc就可以了。但有一种情况是需要在Linux下安装vlc的:我们的音视频拉流软…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

js 设置3秒后执行
如何在JavaScript中延迟3秒执行操作 在JavaScript中,要设置一个操作在指定延迟后(例如3秒)执行,可以使用 setTimeout 函数。setTimeout 是JavaScript的核心计时器方法,它接受两个参数: 要执行的函数&…...

Tauri2学习笔记
教程地址:https://www.bilibili.com/video/BV1Ca411N7mF?spm_id_from333.788.player.switch&vd_source707ec8983cc32e6e065d5496a7f79ee6 官方指引:https://tauri.app/zh-cn/start/ 目前Tauri2的教程视频不多,我按照Tauri1的教程来学习&…...
