二叉树(1)
1 树概念及结构
1.1树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。
把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
- 有一个特殊的结点,称为根结点,根节点没有前驱结点。
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继。
- 因此,树是递归定义的。

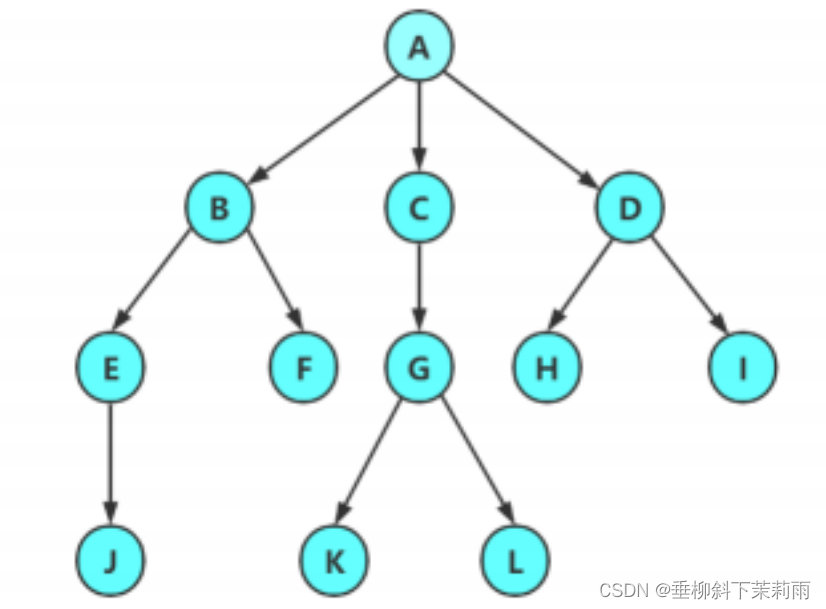
注意:树形结构中,子树之间不能有交集,否则就不是树形结构

以上几种非树,都被称作图。这个我们后面会讲述。
1.2 树的相关概念
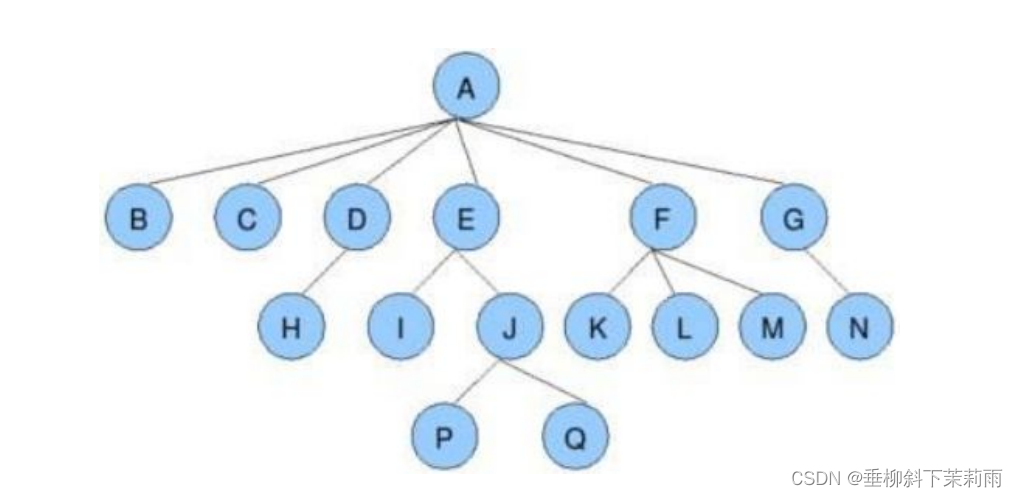
- 节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
- 叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
- 非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
- 兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
- 树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
- 节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
- 森林:由m(m>0)棵互不相交的树的集合称为森林;(并查集就是森林)
一个树只能分为:一个根+N个子树。
1.3 树的表示
这里使用 “左孩子右兄弟” 表示法。

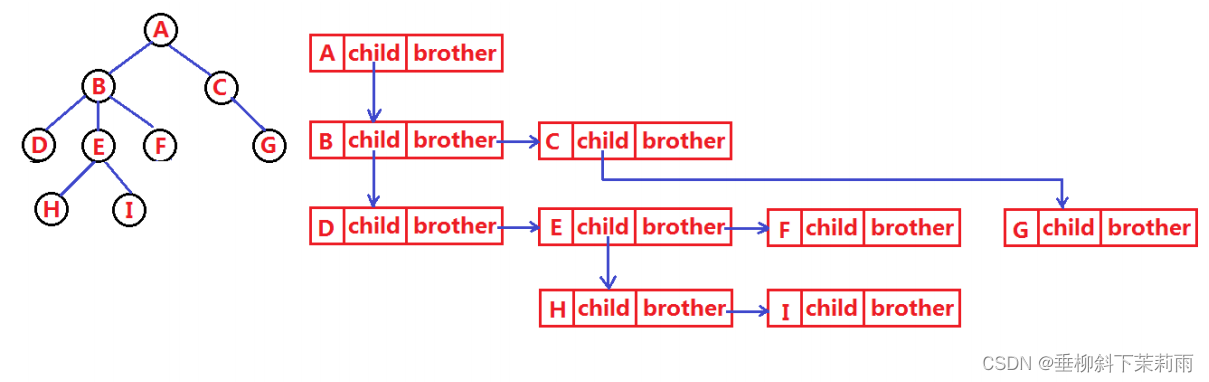
1.4 树在实际中的运用(表示文件系统的目录树结构)
2 二叉树概念及结构
2.1 概念
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 由一个根节点加上两棵别称为左子树和右子树的二叉树组成

从上图可以看出:1. 二叉树不存在度大于2的结点2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
不能说二叉树一定度为2,例子如下。但是度为2的树就是二叉树。
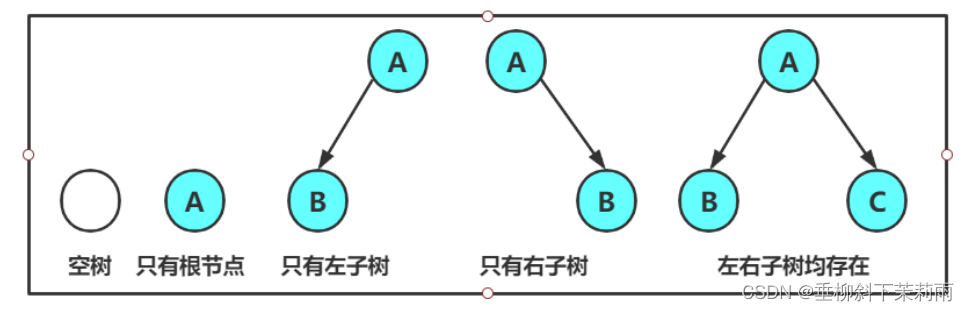
二叉树是一个特殊的树。
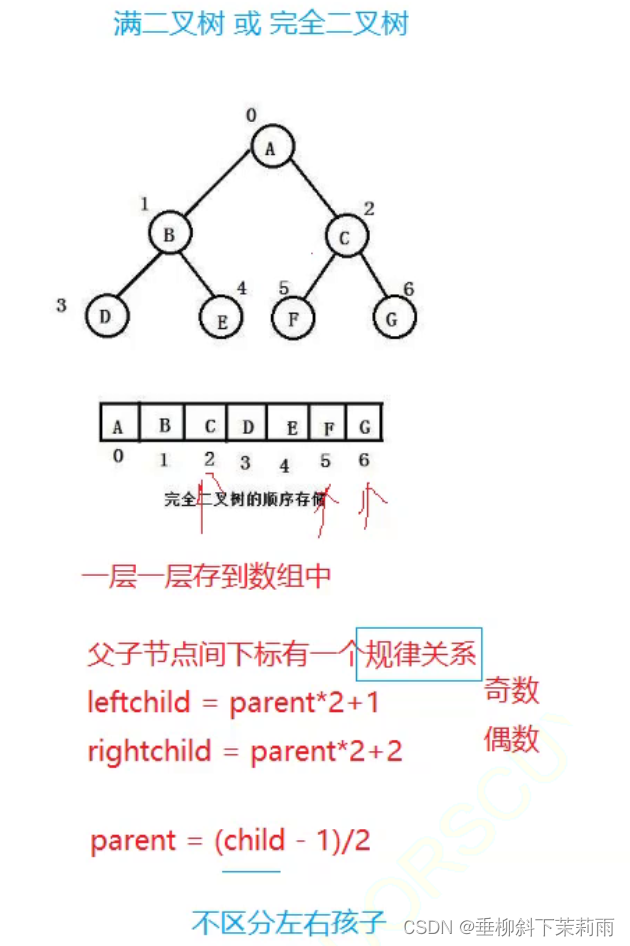
2.2 特殊的二叉树


2.3 二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
1. 顺序存储顺序结构存储就是使用 数组来存储 ,一般使用数组 只适合表示完全二叉树 ,因为不是完全二叉树有空间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们后面的章节会专门讲解。二叉树顺 序存储在物理上是一个数组,在逻辑上是一颗二叉树。 2. 链式存储二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链,后面课程学到高阶数据结构如红黑树等会用到三叉链。
2. 链式存储二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链,后面课程学到高阶数据结构如红黑树等会用到三叉链。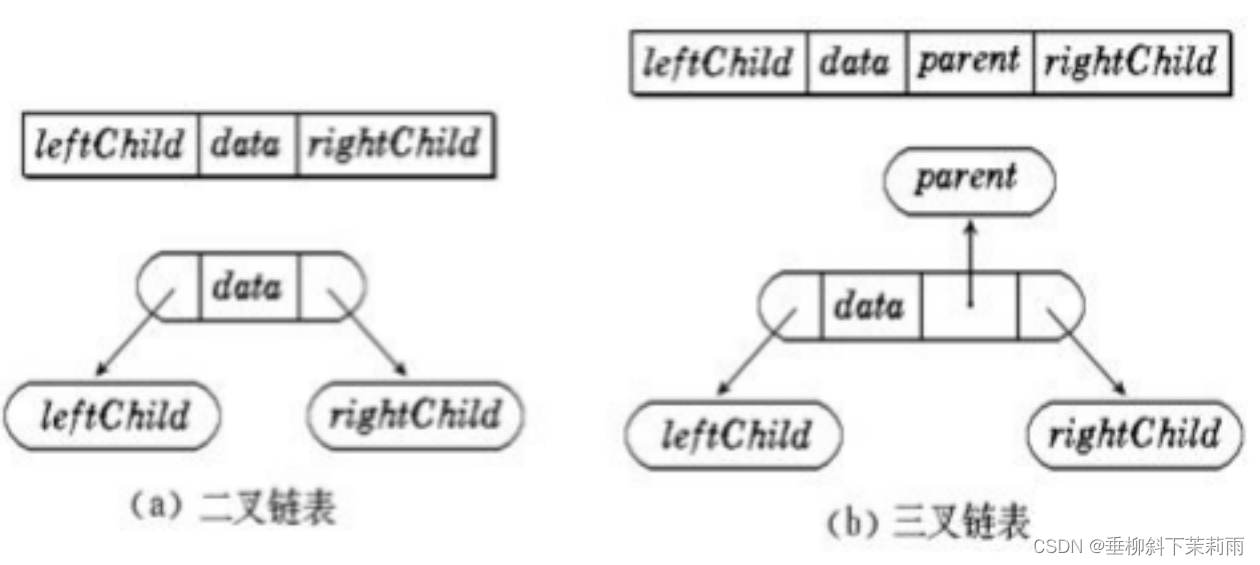


二叉链表一般用于:搜索二叉树 =》 AVL树 和 红黑树。
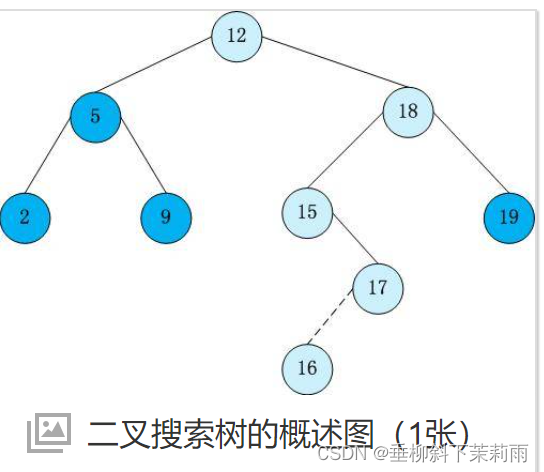 最多查找高度次。
最多查找高度次。
3 堆的概念
3.1 堆的概念
- 堆总是一棵完全二叉树。
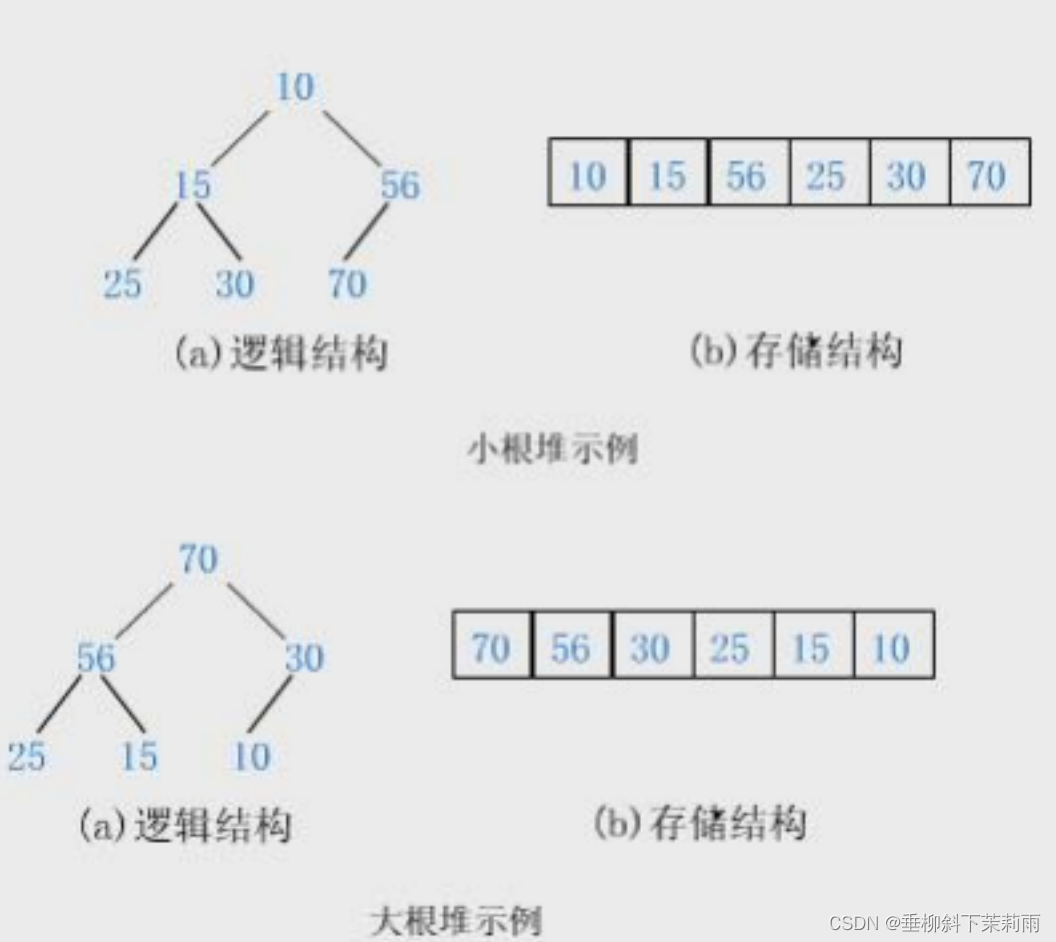 堆一般是把数组数据看作一个完全二叉树。
堆一般是把数组数据看作一个完全二叉树。
小堆要求:任意一个父亲<=孩子。
大堆要求:任意一个父亲>=孩子。
- 有序数组一定是堆,但是堆不一定有序。
3.2 堆的意义
1、堆排序。O(N*logN)
2、top k问题
3.3 选择题
1.下列关键字序列为堆的是:(A)
A 100,60,70,50,32,65
B 60,70,65,50,32,100
C 65,100,70,32,50,60
D 70,65,100,32,50,60
E 32,50,100,70,65,60
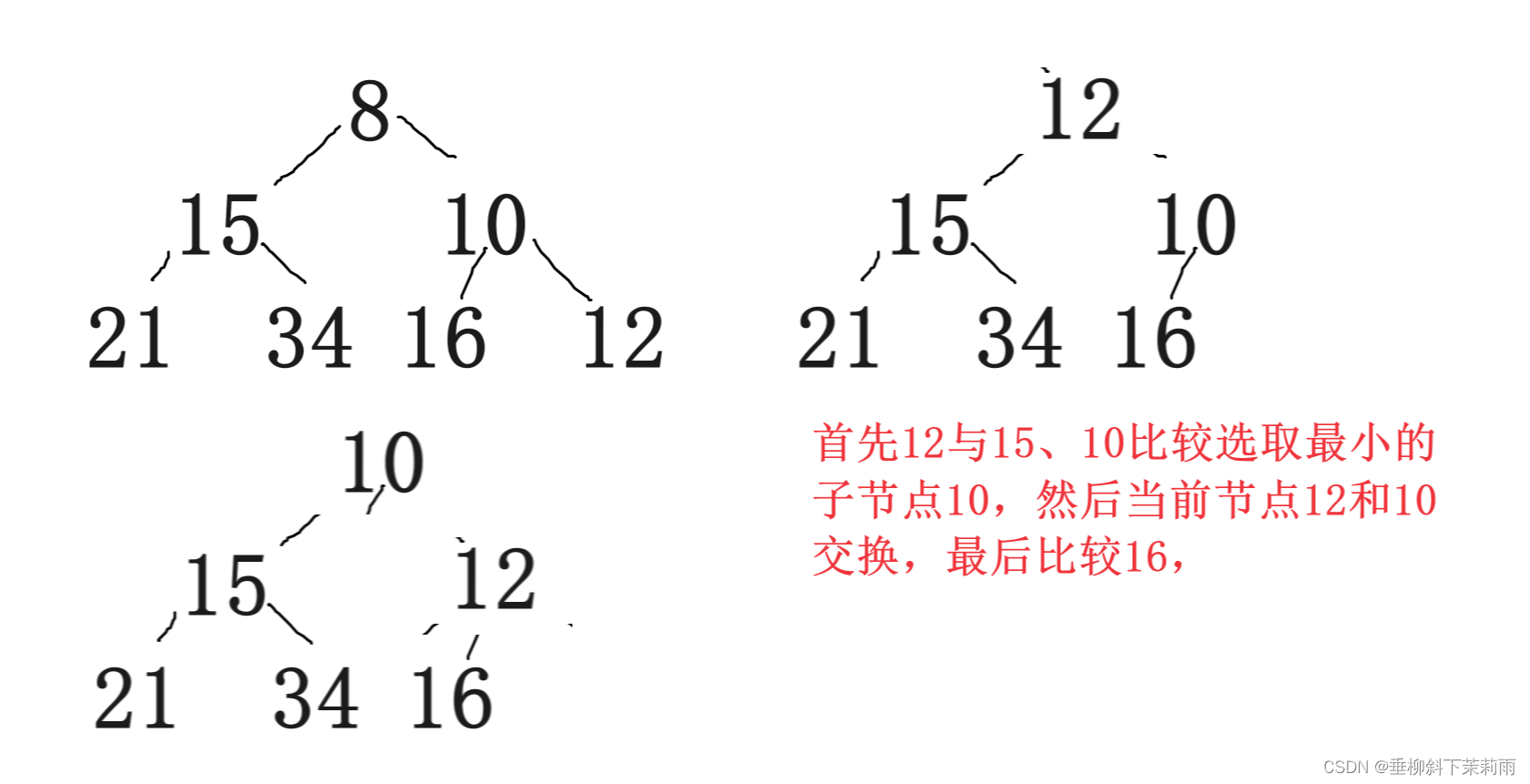
F 50,100,70,65,60,322.已知小根堆为8,15,10,21,34,16,12,删除关键字 8 之后需重建堆,在此过程中,关键字之间的比较次数是(C)。
A 1
B 2
C 3
D 4
3.一组记录排序码为(5 11 7 2 3 17),则利用堆排序方法建立的初始堆为(C)
A(11 5 7 2 3 17)
B(11 5 7 2 17 3)
C(17 11 7 2 3 5)
D(17 11 7 5 3 2)
E(17 7 11 3 5 2)
F(17 7 11 3 2 5)4.最小堆[0,3,2,5,7,4,6,8],在删除堆顶元素0之后,其结果是(C)
A[3,2,5,7,4,6,8]
B[2,3,5,7,4,6,8]
C[2,3,4,5,7,8,6]
D[2,3,4,5,6,7,8]
相关文章:
二叉树(1)
1 树概念及结构 1.1树的概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。 把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。 有一个特殊的结点&a…...

ArcGIS Pro字段编号相关代码
字段属于SHP文件的重要组成部分,在某些时候需要对字段进行编号,这里为大家介绍一下字段编号相关的代码,希望能对你有所帮助。 数据来源 教程所使用的数据是从水经微图中下载的POI数据,除了POI数据,常见的GIS数据都可…...

AJAX-URL查询参数
定义:浏览器提供给服务器的额外信息,让服务器返回浏览器想要的数据 http://xxxx.com/xxx/xxx?参数名1值1&参数名2值2 axios语法 使用axios提供的params选项 注意:axios在运行时把参数名和值,会拼接到url?参数名值 axios(…...
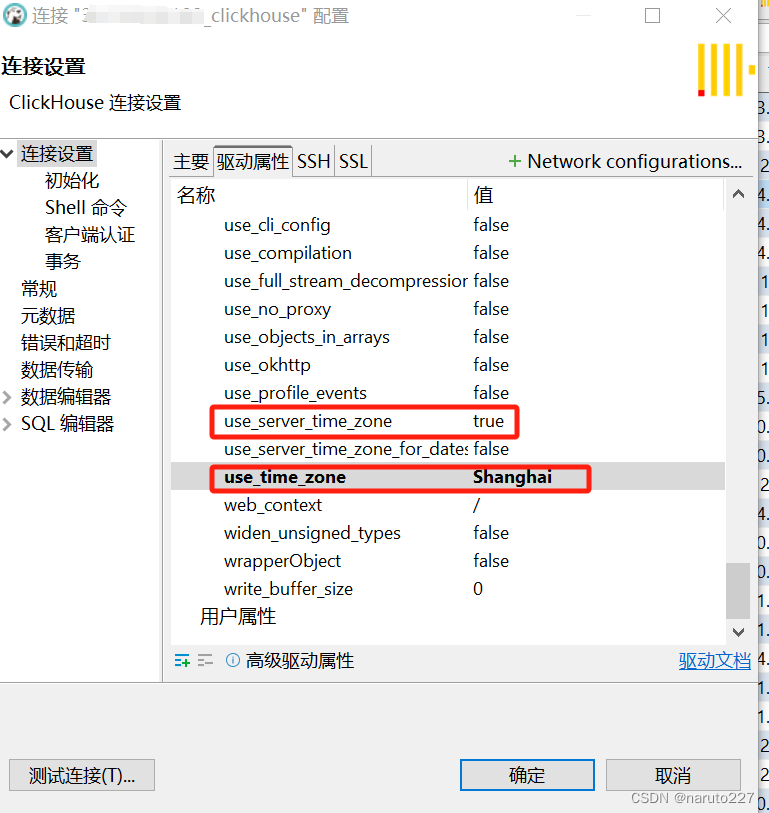
DBeaver连接ClickHouse,时间少了8小时
文章目录 业务场景问题描述解决办法 业务场景 表字段time,类型为Datetime,插入时间格式为“yyyy-MM-dd HH:mm:ss” 问题描述 插入表中的时间比正常给的时间少了8小时。如,给定时间为: 2024-01-30 14:52:08 在表中显示的时间为&…...
)
week03day03(文件操作、正则表达式1)
一、文件操作 1.数据持久化(数据本地化) -- 将数据保存在硬盘 程序中的数据默认是保存在运行内存中的,保存在运行内存中的数据在程序运行结束后会自动释放。如果希望在程序结束后,数据仍可以使用&…...

【数据分享】1929-2023年全球站点的逐年最高气温数据(Shp\Excel\免费获取)
气象数据是在各项研究中都经常使用的数据,气象指标包括气温、风速、降水、湿度等指标,其中又以气温指标最为常用!说到气温数据,最详细的气温数据是具体到气象监测站点的气温数据! 之前我们分享过1929-2023年全球气象站…...
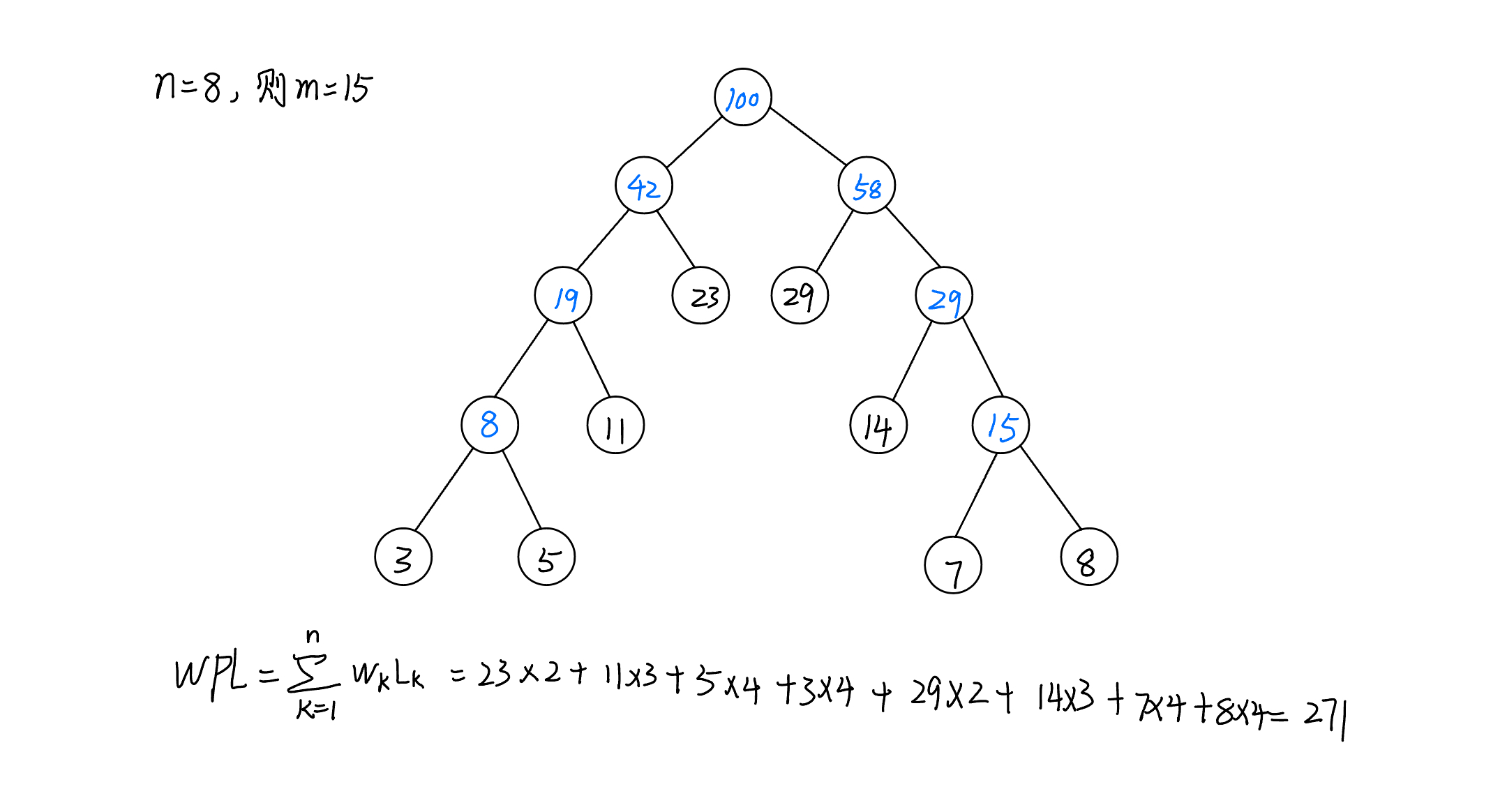
数据结构—基础知识:哈夫曼树
文章目录 数据结构—基础知识:哈夫曼树哈夫曼树的基本概念哈夫曼树的构造算法哈夫曼树的构造过程哈夫曼算法的实现算法:构造哈夫曼树 数据结构—基础知识:哈夫曼树 哈夫曼树的基本概念 哈夫曼(Huffman)树又称最优树&…...
复习提纲24)
计算机网络(第六版)复习提纲24
3 传输控制协议TCP概述 A TCP最主要的特点 1 面向连接的传输层协议 2 每一条TCP连接只能有两个端点,且只能是点对点的 3 提供可靠交付的服务(无差错、不丢失、不重复、不乱序) 4 全双工通信,两端设有发送缓存和接收缓存 5 面向字节…...

[机器学习]TF-IDF算法
一.TF-IDF算法概述 什么是TF-IDF? 词频-逆文档频率(Term Frequency-Inverse Document Frequency,TF-IDF)是一种常用于文本处理的统计方法,可以评估一个单词在一份文档中的重要程度。简单来说就是可以用于文档关键词的提…...

Loadbalancer如何优雅分担服务负荷
欢迎来到我的博客,代码的世界里,每一行都是一个故事 Loadbalancer如何优雅分担服务负荷 前言Loadbalancer基础:数字世界的分配大师1. 分发请求:2. 健康检查:3. 会话保持:4. 可伸缩性:5. 负载均衡…...
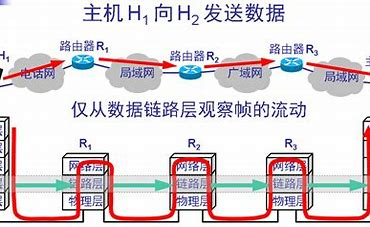
计算机网络——链路层(1)
计算机网络——链路层(1) 小程一言专栏链接: [link](http://t.csdnimg.cn/ZUTXU)前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家, [跳转到网站](https://www.captainbed.…...
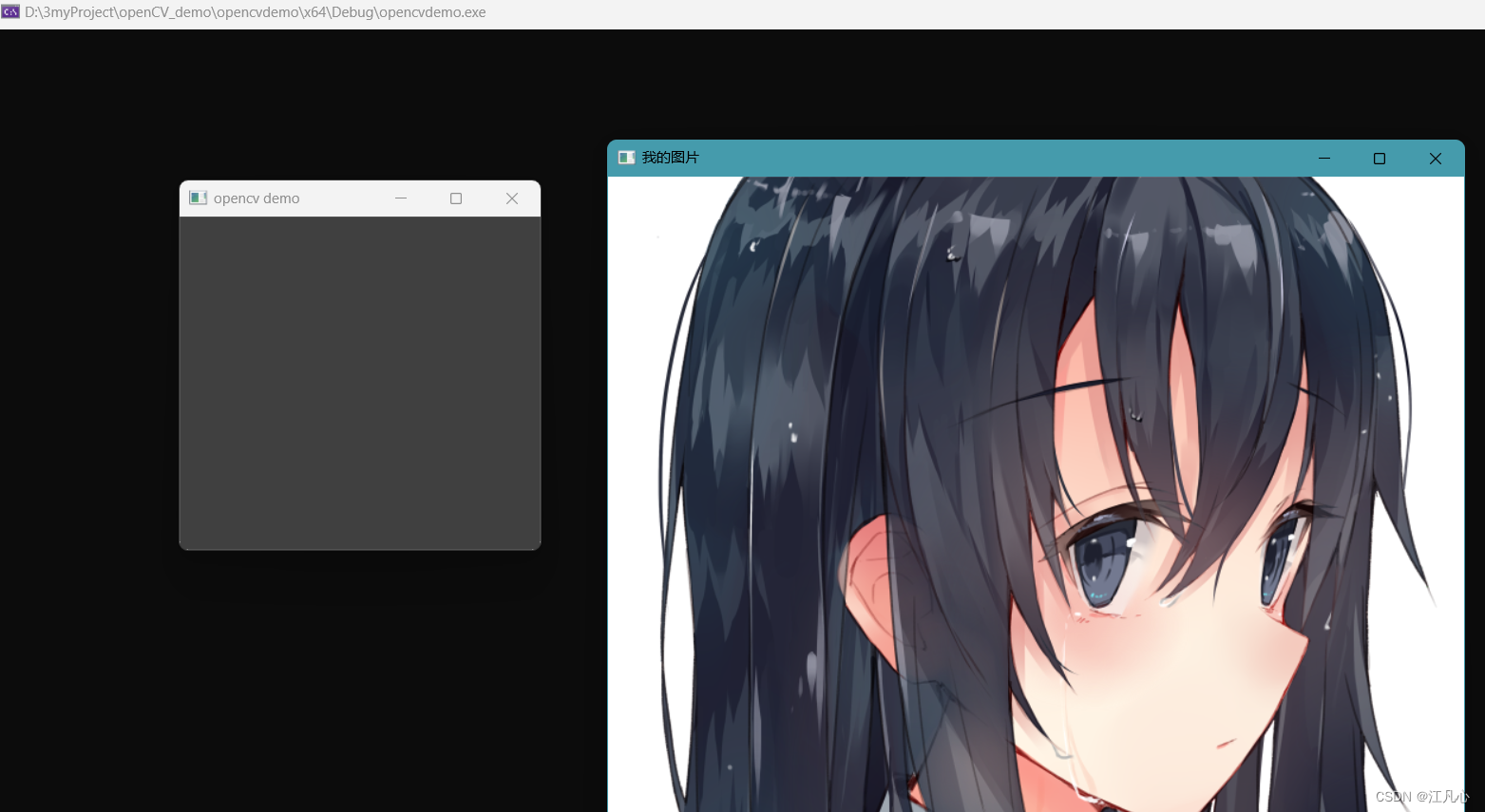
OpenCV 0 - VS2019配置OpenCV
1 配置好环境变量 根据自己的opencv的安装目录配置 2 新建一个空项目 3 打开 视图->工具栏->属性管理器 4 添加新项目属性表 右键项目名(我这是opencvdemo)添加新项目属性表,如果有配置好了的属性表选添加现有属性表 5 双击选中Debug|x64的刚添加的属性表 6 (重点)添…...

eCos flash模拟EEPROM实现NV系统
Flash需要擦除的原因:先擦除后写入的原因是为了工业上制作方便,即物理实现方便。 #include <cyg/infra/diag.h> #include <cyg/io/flash.h> #include <stdarg.h> #include <stdio.h> #include <stdlib.h> // SPI flash…...

【MongoDB】跨库跨表查询(python版)
MongoDB跨表跨库查询 1.数据准备:2.跨集合查询3.跨库查询应该怎么做? 讲一个简单的例子,python连接mongodb做跨表跨库查询的正确姿势 1.数据准备: use order_db; db.createCollection("orders"); db.orders.insertMan…...
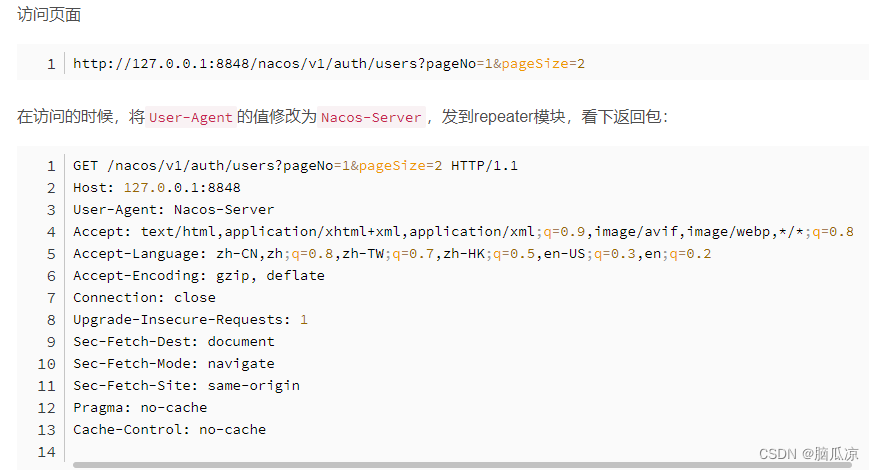
Ruoyi-Cloud-Plus_Nacos配置服务漏洞CVE-2021-29441_官方解决方法以及_修改源码解决---SpringCloud工作笔记199
CVE-2021-29441 这个漏洞是Nacos的,通过使用postman,直接访问接口: 就可以直接添加nacos的用户 Nacos是Alibaba的一个动态服务发现、配置和服务管理平台。攻击者通过添加Nacos-Server的User-Agent头部将可绕过(nacos.core.auth.enabled=true)鉴权认证,从而进行API操作。 …...
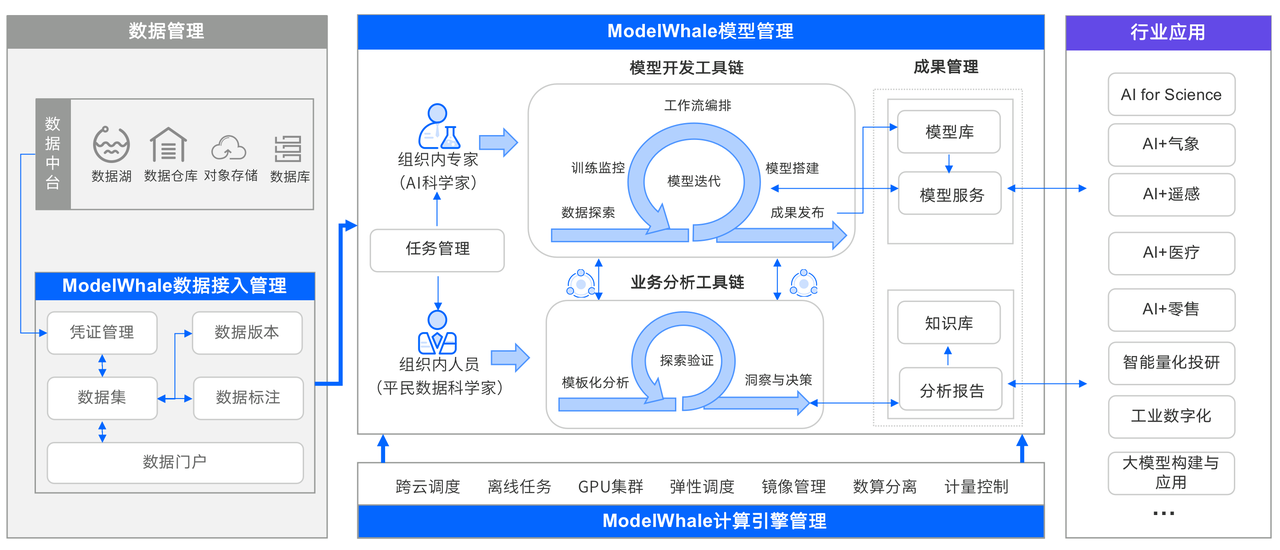
和鲸科技与智谱AI达成合作,共建大模型生态基座
近日,上海和今信息科技有限公司(简称“和鲸科技”)与北京智谱华章科技有限公司(简称“智谱AI”)签订合作协议,双方将携手推动国产通用大模型的广泛应用与行业渗透,并积极赋能行业伙伴探索领域大…...
计算机网络实验五
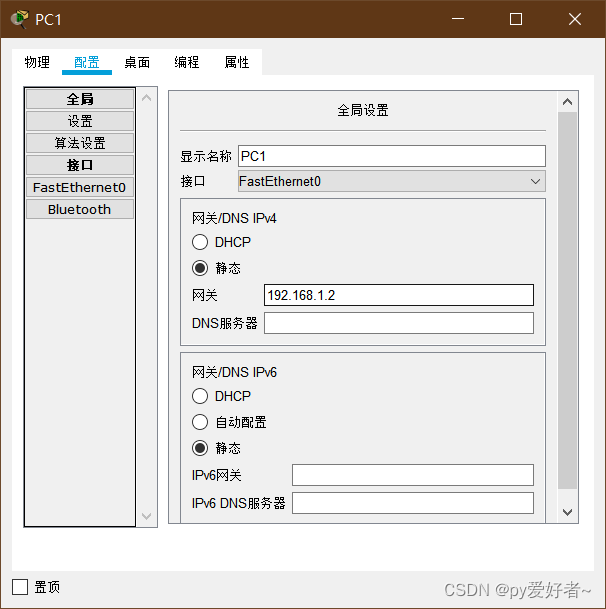
目录 实验五 路由器基本配置 1、实验目的 2、实验设备 3、网络拓扑及IP地址分配 4、实验过程 (1)路由器设备名称的配置 (2)路由器每日提示信息配置 (3)路由器端口的IP地址配置 (4&…...

通过 React 来构建界面
1- 通过 React 来构建界面 第1步:下载所需要的二个库文件至本地,如果需要加载指定版本的 react 和 react-dom,可以把 18 替换成所需加载的版本号。 react.js:React中的核心库文件。 // 开发版 https://unpkg.com/react18/umd/rea…...

真机调试,微信小程序,uniapp项目在微信开发者工具中真机调试,手机和电脑要连同一个wifi,先清空缓存,页面从登录页进入,再点真机调试,这样就不会报错了
微信小程序如何本地进行真机调试?_unity生成的微信小程序怎么在电脑上真机测试-CSDN博客 微信小程序 真机调试 注意事项 uniapp项目在微信开发者工具中真机调试,手机和电脑要连同一个wifi,先清空缓存,页面从登录页进入…...

vue3快速入门
文章目录 1. Vue3简介1.1. 性能的提升1.2.源码的升级1.3. 拥抱TypeScript1.4. 新的特性 2. 创建Vue3工程2.1. 基于 vue-cli 创建2.2. 基于 vite 创建(推荐)vite介绍创建步骤项目结构安装插件项目结构总结 2.3. 一个简单的效果Person.vueApp.vue 3. Vue3核…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...