数据结构—动态查找
动态查找介绍
1. 动态查找的引入:当查找表以线性表的形式组织时,若对查找表进行插入、删除或排序操作,就必须移动大量的记录,当记录数很多时,这种移动的代价很大。
2. 动态查找表的设计思想:表结构本身是在查找过程中动态生成的
若表中存在其关键字等于给定值key的记录,表明查找成功;否则插入关键字等于key的记录。
利用树的形式组织查找表,可以对查找表进行动态高效的查找。
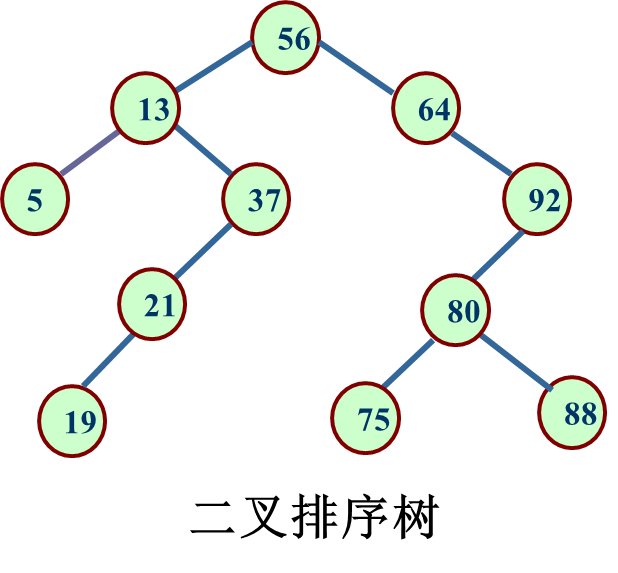
二叉排序树
1. 动态查找表的典型数据结构是二叉排序树,又称二叉查找树,其中序遍历输出为有序序列
二叉排序树是空树或者是具有如下特性的二叉树:
若它的左子树不空,则左子树上所有结点的值均小于根结点的值
若它的右子树不空,则右子树上所有结点的值均大于根结点的值
它的左、右子树也都分别是二叉排序树。
2. 二叉排序树的查找
给定值与根结点比较:
①.若相等,查找成功
②.若小于,查找左子树
③.若大于,查找右子树
实现代码
BSTNode *BST_Serach(BSTNode *T , KeyType key)
{ if (T==NULL) return(NULL) ;else { if (EQ(T->key, key) ) return(T) ;else if ( LT(key, T->key) )return(BST_Serach(T->Lchild, key)) ;else return(BST_Serach(T->Rchild, key)) ;}
}
3. 二叉排序树的插入
二叉排序树是一种动态树表
当树中不存在查找的结点时,作插入操作
新插入的结点一定是叶子结点,只需改动一个结点的指针
该叶子结点是查找不成功时路径上访问的最后一个结点左孩子或右孩子(新结点值小于或大于该结点值)
实现代码
void Insert_BST (BSTNode *T , KeyType key)
{ BSTNode *x ;x=(BSTNode *)malloc(sizeof(BSTNode)) ;x->key=key; x->Lchild=x->Rchild=NULL ; if (T==NULL) T=x ;else{ if (EQ(T->key, x->key) ) return ;/* 已有结点 */else if (LT(x->key, T->key) )Insert_BST(T->Lchild, key) ;else Insert_BST(T->Rchild, key) ; }
}
4. 性能分析
在最好的情况下,二叉排序树为一近似完全二叉树时,其查找深度为log2n量级,即其时间复杂性为O(log2n)
在最坏的情况下,二叉排序树为近似线性表时(如以升序或降序输入结点时),其查找深度为n量级,即其时间复杂性为O(n)
5. 其他
一个无序序列可以通过构造一棵二叉排序树而变成一个有序序列(通过中序遍历)
插入新记录时,只需改变一个结点的指针,相当于在有序序列中插入一个记录而不需要移动其它记录
二叉排序树既拥有类似于折半查找的特性O(log2n),又采用了链表作存储结构
当插入记录的次序不当时(如升序或降序),则二叉排序树深度很深O(n),增加了查找的时间
6. 实现代码
#include<iostream>using namespace std;class node {
public:int data;node *left, *right;node(int value) {data = value;left = right = nullptr;}
};class bitree {
private:bool flag = false;int l;node *root;
public:bitree() {cin >> l;root = nullptr;for (int i = 0; i < l; i++) {int tmp;cin >> tmp;root = insert(root, tmp);}pre_order(root);cout << endl;}//二叉树的创建和插入node *insert(node *q, int t) {if (q == nullptr) {q = new node(t);return q;}if (q->data <= t)q->right = insert(q->right, t);elseq->left = insert(q->left, t);return q;}//独立插入void insert_More() {int t;cin >> t;while (t--) {int tmp;cin >> tmp;insert(root, tmp);pre_order(root);cout << endl;}}//二叉排序树之查找void search_start() {int t;cin >> t;while (t--) {flag = false;int tmp;cin >> tmp;int num = 0;search(root, tmp, num);if (flag)cout << num << endl;elsecout << -1 << endl;}}void search(node *p, int tmp, int &num) {if (p == nullptr)return;num++;if (p->data == tmp) {flag = true;return;}if (tmp > p->data)search(p->right, tmp, num);elsesearch(p->left, tmp, num);}//先序遍历void pre_order(node *p) {if (p == nullptr)return;pre_order(p->left);cout << p->data << " ";pre_order(p->right);}};
平衡二叉树
1. 为解决而擦汗排序树的插入记录次序不当问题, 我们引入了二叉排序(查找)树的另一种形式—平衡二叉树,又被称为AVL树,其特点在于树中每个结点的左右子树深度之差的绝对值不大于1
2. 平衡因子
每个结点附加一个数字, 给出该结点左子树的高度减去右子树的高度所得的高度差,这个数字即为结点的平衡因子balance
AVL树任一结点平衡因子只能取 -1, 0, 1
3. 平衡化旋转,又称为平衡化处理,如果在一棵平衡的二叉查找树中插入一个新结点或者删除一个旧结点,造成了不平衡,此时必须调整树的结构,使之平衡化
平衡化旋转的操作:
每插入一个新结点时, AVL树中相关结点的平衡状态会发生改变
在插入一个新结点后,需要从插入位置沿通向根的路径回溯,检查各结点的平衡因子
如果在某一结点发现高度不平衡,停止回溯。
从发生不平衡的结点起,沿刚才回溯的路径取下两层的结点。对这三个结点进行平衡化处理
平衡化旋转有四种:
单向右旋,LL型,LL是指不平衡的三结点是双亲-左孩子-左孩子
单向左旋,RR型,RR是指不平衡的三结点是双亲-右孩子-右孩子
先左后右双向旋转,LR型,LR是指不平衡的三结点是双亲-左孩子-右孩子
先右后左双向旋转,RL型,RL是指不平衡的三结点是双亲-右孩子-左孩子
注意:英文类型简称是指不平衡状态,不是指旋转方向
注意:中文旋转名称是指旋转方向
B树
B树是一种多路平衡查找树,应用内存和磁盘间的查找
B树又分B-树、B+树,一般把B-树称为B树
B-树
1. m阶B-树规定:
⑴ 根结点或者是叶子,或者至少有两棵子树,至多有m棵子树;
⑵ 除根结点外,所有非终端结点至少有ém/2ù棵子树,至多有m棵子树
⑶ 所有叶子结点都在树的同一层上;
⑷ 每个结点应包含如下信息:
(n,A0,K1,A1,K2,A2,… ,Kn,An)
n是n个关键字,A是孩子指针,K是关键字
(5) Ki<Ki+1 且Ai所指向的子树中所有结点的关键字都在Ki和Ki+1之间
2. B-树的特点
m阶B-树即m叉树,m是树的度
m是指树结点最多包含m个孩子指针
每个树结点中,关键字的数量比孩子指针数量少1
根结点可以有2到m个孩子指针
叶子结点的关键字数量不受限制,孩子指针都是空指针,数量无意义
中间结点包含ém/2ù到m个孩子指针,即包含ém/2ù-1到m-1个关键字
B+树
1. 基本概念
在实际的文件系统中,基本上不使用B-树,而是使用B-树的一种变体,称为m阶B+树。
B+树与B-树的主要不同是叶子结点中存储记录。
在B+树中,所有的非叶子结点可以看成是索引,而其中的关键字是作为“分界关键字”,用来界定某一关键字的记录所在的子树。
即B+树中,所有结果信息都在叶子,查找结束必定在叶子
2. B+树的特点
与B-树相比,对B+树不仅可以从根结点开始按关键字随机查找,而且可以从最小关键字起,按叶子结点的链接顺序进行顺序查找。
在B+树上进行随机查找、插入、删除的过程基本上和B-树类似。
在B+树上进行随机查找时,若非叶子结点的关键字等于给定的K值,并不终止,而是继续向下直到叶子结点(只有叶子结点才存储记录), 即无论查找成功与否,都走了一条从根结点到叶子结点的路径。
平衡二叉树AVL-Tree的改进——红黑树RB-Tree
红黑树是一种不那么严格的平衡二叉树
它允许不平衡达到一倍,即左右子树高度差可以达到一倍
RBT是用非严格的平衡来换取增删结点时候旋转次数的降低,任何不平衡都会在三次旋转之内解决
AVL是严格平衡树,因此在增加或者删除结点的时候,根据不同情况,旋转的次数比红黑树要多。所以红黑树的插入效率更高!!
相关文章:

数据结构—动态查找
动态查找介绍 1. 动态查找的引入:当查找表以线性表的形式组织时,若对查找表进行插入、删除或排序操作,就必须移动大量的记录,当记录数很多时,这种移动的代价很大。 2. 动态查找表的设计思想:表结构本身是…...

Tarjan算法学习笔记
目录 无向图的割点与桥 时间戳: 搜索树: 追溯值: 割边判定法则: 割点判定法则: 无向图的双连通分量 定理: 边双连通分量(e-DCC)的求法: e-DCC的缩点: 有向图的连通性 追…...

vue 项目涉及的焦点聚焦、格式化日期、判断是否为对象或数组、判断是否为空、深拷贝、节流、防抖
焦点聚焦 import Vue from vue // 插件对象(必须有 install 方法, 才可以注入到 Vue.use 中) export default {install () {Vue.directive(fofo, {inserted (el) {el el.querySelector(input)el.focus()}})} }格式化日期格式 export const formatDate (time) > {// 将xx…...
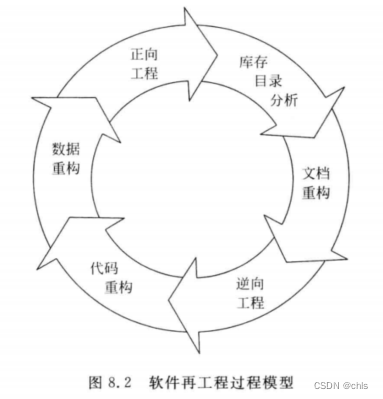
软件工程知识梳理6-运行和维护
软件维护需要的工作量很大,大型软件的维护成本高达开发成本的4倍左右。所以,软件工程的主要目的就是要提高软件的可维护性,减少软件维护所需要的工作量,降低软件系统的总成本。 定义:软件已经交付使用之后,…...

docker- php7.4
安装 gd拓展 anzhuanga在Dockerfile里面安装php7.4的GD库 - 知乎 apt update apt install -y libwebp-dev libjpeg-dev libpng-dev libfreetype6-devdocker-php-source extractdocker-php-ext-configure gd \ --with-jpeg/usr/include \ --with-freetype/usr/include/docker-…...

开发一个Android App,在项目中完成添加联系人的功能,通过ContentResolver向系统中添加联系人信息。
实现步骤: (1)添加动态联系人的权限。 (2)创建Activity和布局文件,添加输入框和按钮等控件。 (3)完成添加联系人的功能。 代码文件如下: activity_main.xml文件 <!…...

Flume搭建
压缩包版本:apache-flume-1.9.0-bin.tar 百度盘链接:https://pan.baidu.com/s/1ZhSiePUye9ax7TW5XbfWdw 提取码:ieks 1.解压 tar -zxvf /opt/software/apache-flume-1.9.0-bin.tar.gz -C /opt/module/ 2. 修改文件名 [rootbigdata1 opt]…...

Web APIs 1 DOM操作
Web APIs 1 引入:const优先Web API 基本认知01 作用和分类02 什么是DOM03 DOM树04 DOM对象 获取DOM对象01 根据CSS选择器获取02 其他获取DOM元素方法 操作元素内容01 innerText 属性02 innerHTML 属性 操作元素属性操作元素的常用属性操作元素的样式属性操作表单元素…...
dvwa,xss反射型lowmedium
xss,反射型,low&&medium low发现xss本地搭建实操 medium作为初学者的我第一次接触比较浅的绕过思路high low 发现xss 本关无过滤 <script>alert(/xss/)</script> //或 <script>confirm(/xss/)</script> //或 <scr…...

从云计算到物联网:虚拟化技术的演变与嵌入式系统的融合
文章目录 一、硬件性能提升:摩尔定律与嵌入式虚拟化二、CPU多核技术:为嵌入式虚拟化提供支持三、业务负载整合:嵌入式虚拟化的核心需求四、降低硬件成本:虚拟化技术的经济效益五、软件重用与移植:虚拟化技术的优势六、…...

linux 文件查看 head 、 cat 、 less 、tail 、grep
查看文件详细信息 stat 文件 cat 》》适合显示小文件【行数比较少】,如果行数较多,屏幕显示不完整(如果虚拟操作,是无法上下键的,或者滚动鼠标的,第三方 xsheel,crt 可以方向键查看…...
)
13.2 Web与Servlet进阶(❤❤)
13.2 Web与Servlet进阶 1. 请求与响应1.1 URL与URI1.2 HTTP请求的结构1. 结构2.后端获取访问工具类型:getHeader().toLowerCase方法1.3 响应的结构1. 结构2. 响应常见状态码3. 后端设置响应参数4. 响应的ContentType作用1.4 请求转发与响应重定向应用1. 请求转发:getRequestDis…...
)
记录解决报错--vue前后端分离,接口401(Unauthorized)
1.场景 前端访问不了后端接口。报错401。 2.解决步骤 ①在页面console.log(111)查看走到代码的位置没有。(走到了,没问题) ②查看vue.config.js配置。这段配置就是vue访问api的url。(没问题) devServer: {port: 80…...
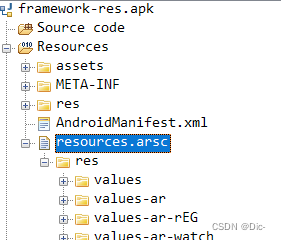
【笔记】Android 常用编译模块和输出产物路径
模块&产物路径 具体编译到软件的路径要看编译规则的分区,代码中模块编译输出的产物基本对应。 Android 代码模块 编译产物路径设备adb路径Comment 模块device/mediatek/system/common/ 资源overlay/telephony/frameworks/base/core 文件举例res/res/values-m…...

部署私有知识库项目FastGPT
FastGPT 是一个基于 LLM 大语言模型的知识库问答系统,提供开箱即用的数据处理、模型调用等能力。同时可以通过 Flow 可视化进行工作流编排,从而实现复杂的问答场景。 项目文档: [快速了解 FastGpt | FastGptFastGPT 是一个基于 LLM 大语言模型的知识库问答系统,提供开箱即…...

【2024-02-02】华为秋招笔试三道编程题解
恭喜发现宝藏!搜索公众号【TechGuide】回复公司名,解锁更多新鲜好文和互联网大厂的笔经面经。 作者TechGuide【全网同名】 订阅专栏: 【专享版】2024最新大厂笔试真题解析,错过必后悔的宝藏资源! 第一题:找…...
银行数据仓库体系实践(8)--主数据模型设计
主数据区域中保留了数据仓库的所有基础数据及历史数据,是数据仓库中最重要的数据区域之一,那主数据区域中主要分为近源模型区和整合(主题)模型区。上一节讲到了模型的设计流程如下图所示。那近源模型层的设计在第2.3和3这两个步骤…...

vue在main.js中引入三方插件不生效的原因
有的时候需要比较复杂的功能,但是自己实现比较复杂的话,可以引入第三方插件.如果这个第三方插件需要全局都使用的话,可以在main.js中进行引入. 比如router elementplus之类的. import { createApp } from vue import ElementPlus from element-plus import element-plus/dist/…...

chatgpt搭建
chatgpt两步搭建大法 部署docker环境 下载docker curl -fsSL https://get.docker.com -o get-docker.sh安装docker sh get-docker.sh运行docker服务 systemctl start docker查看运行状态 systemctl status docker设置docker开机自启 systemctl enable docker部署chatgpt…...

vue基本理解
1、js闭包,作用?? 闭包是指在一个函数内部,可以访问外部函数的变量,即使外部函数已经执行完毕。闭包的作用有: 保护变量:闭包可以保护函数内部的变量,使其不受外部环境的影响。实现…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
