快递员的烦恼 - 华为OD统一考试
OD统一考试(C卷)
分值: 200分
题解: Java / Python / C++

题目描述
快递公司每日早晨,给每位快递员推送需要淡到客户手中的快递以及路线信息,快递员自己又查找了一些客户与客户之间的路线距离信息,请你依据这些信息,给快递员设计一条最短路径,告诉他最短路径的距离。
-
不限制快递包裹送到客户手中的顺序,但必须保证都送到客户手中;
-
用例保证一定存在投递站到每位客户之间的路线,但不保证客户与客户之间有路线,客户位置及投递站均允许多次经过;
-
所有快递送完后,快递员需回到投递站;
输入描述
首行输入两个正整数n、m.
接下来n行,输入快递公司发布的客户快递信息,格式为:客户id 投递站到客户之间的距离distance
再接下来的m行,是快递员自行查找的客户与客户之间的距离信息,格式为:客户1id 客户2id distance
在每行数据中,数据与数据之间均以单个空格分割规格:
0 <=n <= 10
0 <= m <= 10
0 < 客户id <= 1000
0 < distance <= 10000
输出描述
最短路径距离,如无法找到,请输出-1
示例1
输入:
2 1
1 1000
2 1200
1 2 300输出:
2500说明:
快递员先把快递送到客户1手中,接下来直接走客户1到客户2之间的直通线路,最后走投递站和客户2之间的路,回到投递站,距离为1000+300+1200= 2500
示例2
输入:
5 1
5 1000
9 1200
17 300
132 700
500 2300
5 9 400输出:
9200
题解
这道题目属于图论中的最短路径问题。题目要求找到一条路径,使得快递员从投递站出发,依次经过所有客户,最后回到投递站,使得路径的总距离最短。
首先,我们需要构建一个图,图中的节点表示投递站和所有客户,边表示它们之间的距离。由于题目中给出了客户之间的距离信息,我们可以使用 Floyd 算法来计算任意两点之间的最短距离。
接下来,我们使用动态规划来求解最短路径。定义
dp[state][last]表示当前情况下已经投递的客户集合为state,上一次投递的客户为last时,已经走过的最短距离。状态转移方程为:dp[state | (1 << last)][last] = min(dp[state | (1 << last)][last], dp[state][i] + dist[i][last])其中,
state为二进制表示的已经投递的客户集合,state | (1 << last)表示将state中last位置设置为1,last表示上一次投递的状态。dist[i][last]表示投递的客户的最短距离。时间复杂度
Floyd-Warshall算法的时间复杂度为O(n3),动态规划的时间复杂度为O(2n * n2),总体时间复杂度为O(n3 + 2^n * n^2)。
空间复杂度
空间复杂度主要由存储距离矩阵和动态规划数组决定,为O(n^2 + 2^n * n)。
Java
import java.util.Arrays;
import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;
/*** @author code5bug*/
public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt(), m = scanner.nextInt();int[][] dist = new int[n + 1][n + 1];for (int i = 0; i < dist.length; i++) Arrays.fill(dist[i], Integer.MAX_VALUE);// 客户id 和索引下标的对照表Map<Integer, Integer> idxMap = new HashMap<>();// 初始化客户id 到 投递站(0) 之间的距离for (int idx = 1; idx <= n; idx++) {int cid = scanner.nextInt();int distance = scanner.nextInt();dist[0][idx] = dist[idx][0] = distance;idxMap.put(cid, idx);}// 初始化客户与客户之间的距离for (int i = 0; i < m; i++) {int cid1 = scanner.nextInt(), cid2 = scanner.nextInt(), distance = scanner.nextInt();int idx1 = idxMap.get(cid1), idx2 = idxMap.get(cid2);dist[idx1][idx2] = dist[idx2][idx1] = distance;}// Floyd-Warshall算法 求出所有点之间的最短距离 时间复杂度为O(n^3)for (int k = 0; k <= n; k++) {dist[k][k] = 0; // 自己到自己的距离为0for (int i = 0; i <= n; i++) {for (int j = 0; j <= n; j++) {dist[i][j] = Math.min(dist[i][j], dist[i][k] + dist[k][j]);}}}// dp[state][last] 当前情况走过的最短距离// state 表示已经投递的客户 (指定二进制位为1表示已经投递),last表示上一次投递的客户int[][] dp = new int[1 << (n + 1)][n + 1];for (int i = 0; i < (1 << (n + 1)); i++) Arrays.fill(dp[i], Integer.MAX_VALUE);dp[1][0] = 0; // 初始状态,在投递站for (int state = 0; state < (1 << (n + 1)); state++) {for (int i = 0; i <= n; i++) {if ((state >> i & 1) == 1 && dp[state][i] != Integer.MAX_VALUE) { // 如果 i 已经投递 且 可达for (int last = 0; last <= n; last++) {dp[state | (1 << last)][last] = Math.min(dp[state | (1 << last)][last], dp[state][i] + dist[i][last]);}}}}System.out.println(dp[(1 << (n + 1)) - 1][0]);}
}
Python
from math import infn, m = map(int, input().split())
dist = [[inf] * (n + 1) for _ in range(n + 1)]# 客户id 和索引下标的对照表
idx_map = {}# 初始化客户id 到 投递站(0) 之间的距离
for idx in range(1, n + 1):cid, distance = map(int, input().split())dist[0][idx] = dist[idx][0] = distanceidx_map[cid] = idx# 初始化客户与客户之间的距离
for _ in range(m):cid1, cid2, distance = map(int, input().split())idx1, idx2 = idx_map[cid1], idx_map[cid2]dist[idx1][idx2] = dist[idx2][idx1] = distance# Floyd-Warshall算法 求出所有点之间的最短距离 时间复杂度为O(n^3)
for k in range(n + 1):dist[k][k] = 0 # 自己到自己的距离为0for i in range(n + 1):for j in range(n + 1):dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])f = [[inf] * (n + 1) for _ in range(1 << (n + 1))]
f[1][0] = 0# dp[state][last] 当前情况走过的最短距离
# state 表示已经投递的客户 (指定二进制位为1表示已范围),last表示上一次投递的客户
dp = [[inf] * (n + 1) for _ in range(1 << (n + 1))]
dp[1][0] = 0 # 初始状态,在投递站for state in range(1 << (n + 1)):for i in range(n + 1):if (state >> i) & 1 and dp[state][i] != inf: # 如果 i 已经投递 且 可达for last in range(n + 1):dp[state | (1 << last)][last] = min(dp[state | (1 << last)][last], dp[state][i] + dist[i][last])print(dp[(1 << (n + 1)) - 1][0])C++
#include <iostream>
#include <vector>
#include <unordered_map>
#include <algorithm>
#include <climits>using namespace std;int main() {int n, m;cin >> n >> m;vector<vector<int>> dist(n + 1, vector<int>(n + 1, INT_MAX));// 客户id 和索引下标的对照表unordered_map<int, int> idxMap;// 初始化客户id 到 投递站(0) 之间的距离for (int idx = 1; idx <= n; idx++) {int cid, distance;cin >> cid >> distance;dist[0][idx] = dist[idx][0] = distance;idxMap[cid] = idx;}// 初始化客户与客户之间的距离for (int i = 0; i < m; i++) {int cid1, cid2, distance;cin >> cid1 >> cid2 >> distance;int idx1 = idxMap[cid1], idx2 = idxMap[cid2];dist[idx1][idx2] = dist[idx2][idx1] = distance;}// Floyd-Warshall算法 求出所有点之间的最短距离 时间复杂度为O(n^3)for (int k = 0; k <= n; k++) {dist[k][k] = 0; // 自己到自己的距离为0for (int i = 0; i <= n; i++) {for (int j = 0; j <= n; j++) {dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);}}}// dp[state][last] 当前情况走过的最短距离// state 表示已经投递的客户 (指定二进制位为1表示已经投递),last表示上一次投递的客户vector<vector<int>> dp(1 << (n + 1), vector<int>(n + 1, INT_MAX));dp[1][0] = 0; // 初始状态,在投递站for (int state = 0; state < (1 << (n + 1)); state++) {for (int i = 0; i <= n; i++) {if ((state >> i & 1) == 1 && dp[state][i] != INT_MAX) { // 如果 i 已经投递 且 可达for (int last = 0; last <= n; last++) {dp[state | (1 << last)][last] = min(dp[state | (1 << last)][last], dp[state][i] + dist[i][last]);}}}}cout << dp[(1 << (n + 1)) - 1][0] << endl;return 0;
}相关练习题
| 题号 | 题目 | 难易 |
|---|---|---|
| LeetCode 2976 | 2976. 转换字符串的最小成本 I | 中等 |
❤️华为OD机试面试交流群(每日真题分享): 加V时备注“华为od加群”
🙏整理题解不易, 如果有帮助到您,请给点个赞 ❤️ 和收藏 ⭐,让更多的人看到。🙏🙏🙏
相关文章:

快递员的烦恼 - 华为OD统一考试
OD统一考试(C卷) 分值: 200分 题解: Java / Python / C 题目描述 快递公司每日早晨,给每位快递员推送需要淡到客户手中的快递以及路线信息,快递员自己又查找了一些客户与客户之间的路线距离信息࿰…...
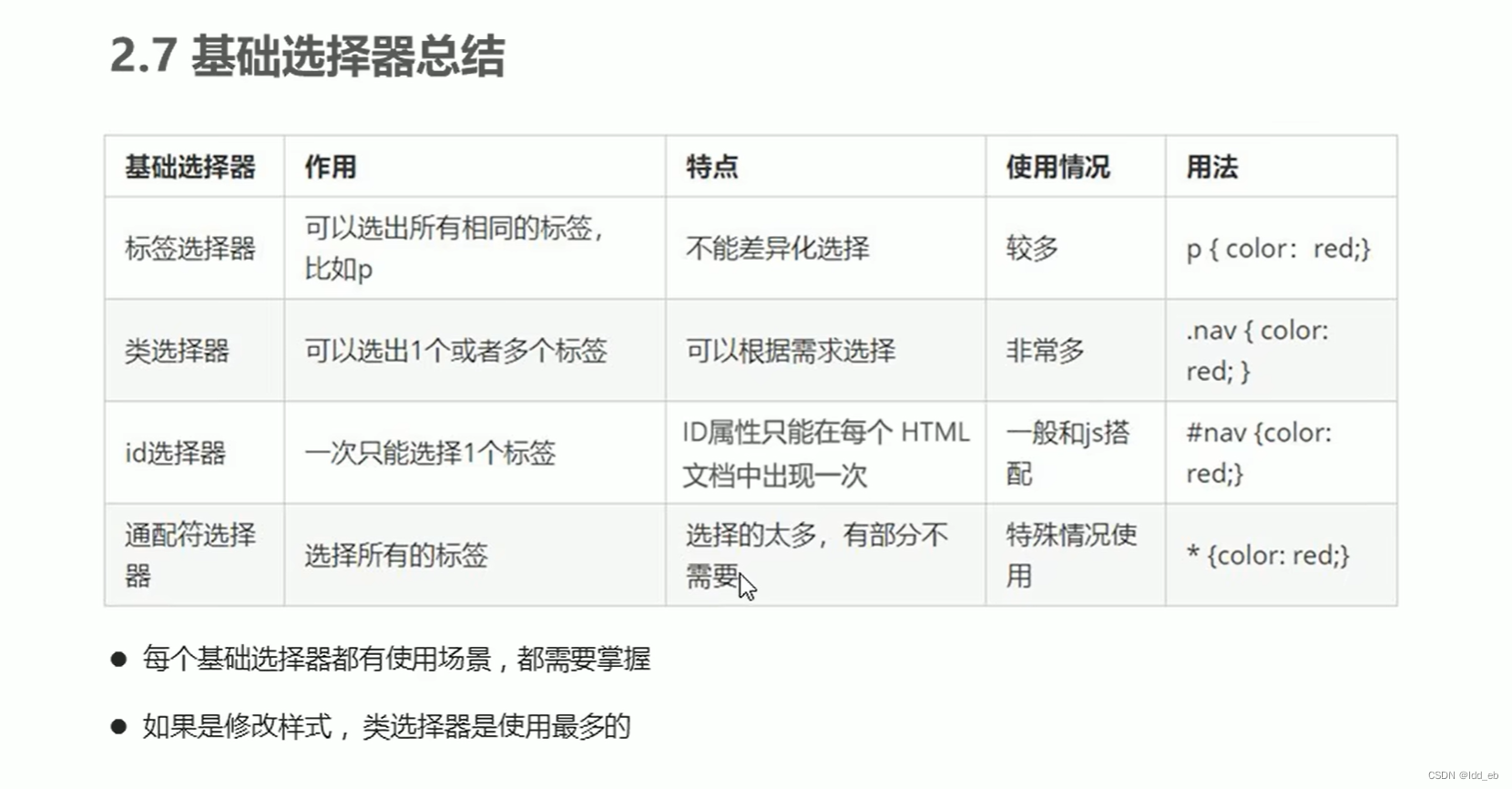
css1基础选择器
大纲 一.标签选择器 比较简单,前面直接写目标标签 二.类选择器 应用 例子 三.多类名选择器(调用时中间用空格隔开) 四.id选择器 应用 五.通配符选择器 应用 六.总结...

【C语言】内联函数总结
内联函数定义 inline关键字是C99标准的型关键字,其作用是将函数展开,把函数的代码复制到每一个调用处。这样调用函数的过程就可以直接执行函数代码,而不发生跳转、压栈等一般性函数操作。可以节省时间,也会提高程序的执行速度。 …...

鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之MenuItemGroup组件
鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之MenuItemGroup组件 一、操作环境 操作系统: Windows 10 专业版、IDE:DevEco Studio 3.1、SDK:HarmonyOS 3.1 二、MenuItemGroup组件 该组件用来展示菜单MenuItem的分组。 子组件 无 接…...

【Linux多线程编程】互斥锁及其使用
1、互斥锁 用于解决竞争问题的一种机制。 什么是竞争,竞争就是多个实体同时获取一个资源,例如多个线程写一个全局变量。 2、Linux如何使用互斥锁 以pthread为例,锁的创建和使用如下: /* 创建锁 */ pthread_mutex_t lock PTHR…...

RabbitMQ_00000
MQ的相关概念 RabbitMQ官网地址:https://www.rabbitmq.com RabbitMQ API地址:https://rabbitmq.github.io/rabbitmq-java-client/api/current/ 什么是MQ? MQ(message queue)本质是个队列,FIFO先入先出,只不过队列中…...

【linux】docker下homeassistant和nodered安装及配置
1、homeassistant安装 从 Docker Hub 上拉取 Home Assistant 的镜像文件 docker pull homeassistant/home-assistant 是运行 Home Assistant 容器 docker run -id --name"homeassistant" --privileged --restart always -p 8123:8123 -e TZAisa/Shanghai --nethost…...

Qt扩展-muParser数学公式解析
muParser数学公式解析 一、概述1. 针对速度进行了优化2. 支持的运算符3. 支持的函数4. 用户定义的常量5. 用户定义的变量6. 自定义值识别回调7. 其他功能 二、内置函数三、内置二元运算符四、三元运算符五、内置常量六、源码引入1. 源码文件2. 编译器开关1. MUP_BASETYPE2.MUP_…...

【Matplotlib】figure方法之图形的保存
🎈个人主页:甜美的江 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:matplotlib 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、交流进…...
)
数据库管理-第142期 DBA?DBA!(20240131)
数据库管理142期 2024-01-31 数据库管理-第142期 DBA?DBA!(20240131)正文总结 数据库管理-第142期 DBA?DBA!(20240131) 作者:胖头鱼的鱼缸(尹海文)…...
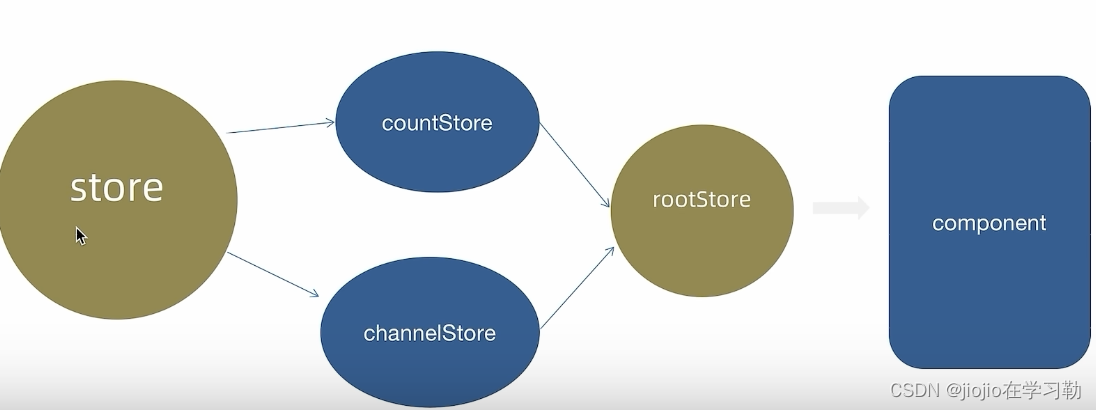
react 之 zustand
zustand可以说是redux的平替 官网地址:https://zustand-demo.pmnd.rs/ 1.安装 npm i zustand2.基础使用 // zustand import { create } from zustand// 1. 创建store // 语法容易出错 // 1. 函数参数必须返回一个对象 对象内部编写状态数据和方法 // 2. set是用来…...

leetcode-回文链表
234. 回文链表 在此对比的值,不是节点 # Definition for singly-linked list. # class ListNode: # def __init__(self, val0, nextNone): # self.val val # self.next next class Solution:def isPalindrome(self, head: Optional[ListNod…...

Pinia:一个Vue的状态管理库
Pinia的使用方法包括以下步骤: 安装Pinia:通过yarn或npm进行安装: yarn命令: yarn add pinianpm命令: npm install pinia创建根存储:在main.ts中引入Pinia插件,并创建一个根存储。这可以通过创建…...
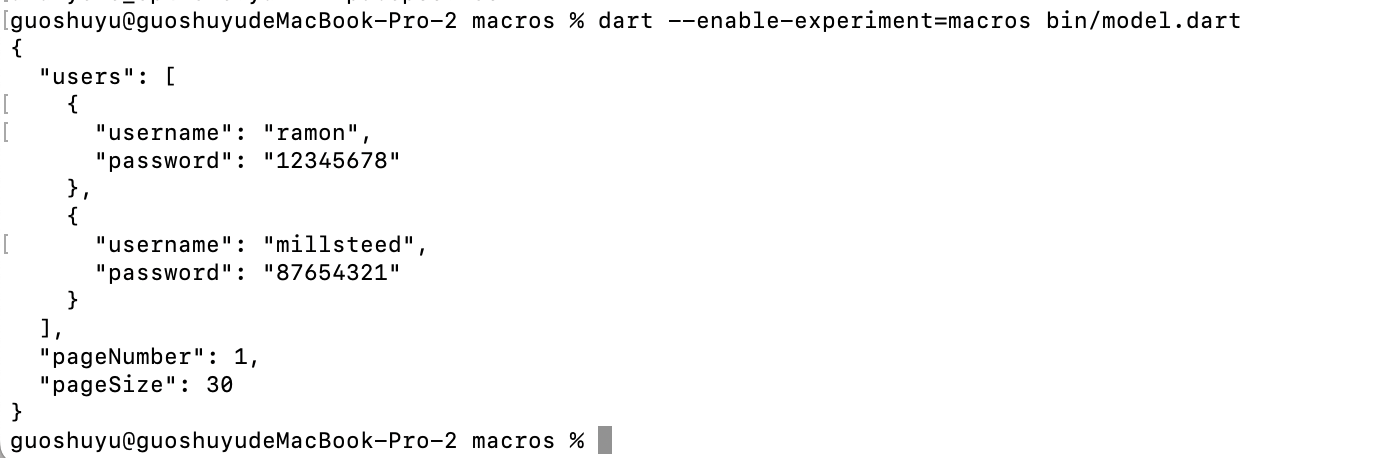
2024 Flutter 重大更新,Dart 宏(Macros)编程开始支持,JSON 序列化有救
说起宏编程可能大家并不陌生,但是这对于 Flutter 和 Dart 开发者来说它一直是一个「遗憾」,这个「遗憾」体现在编辑过程的代码修改支持上,其中最典型的莫过于 Dart 的 JSON 序列化。 举个例子,目前 Dart 语言的 JSON 序列化高度依…...

云计算概述(云计算类型、技术驱动力、关键技术、特征、特点、通用点、架构层次)(二)
云计算概述(二) (云计算类型、技术驱动力、关键技术、特征、特点、通用点、架构层次) 目录 零、00时光宝盒 一、云计算类型(以服务的内容或形态来分) 二、云计算的12种技术驱动力 三、云计算的关键技术 四、云计…...
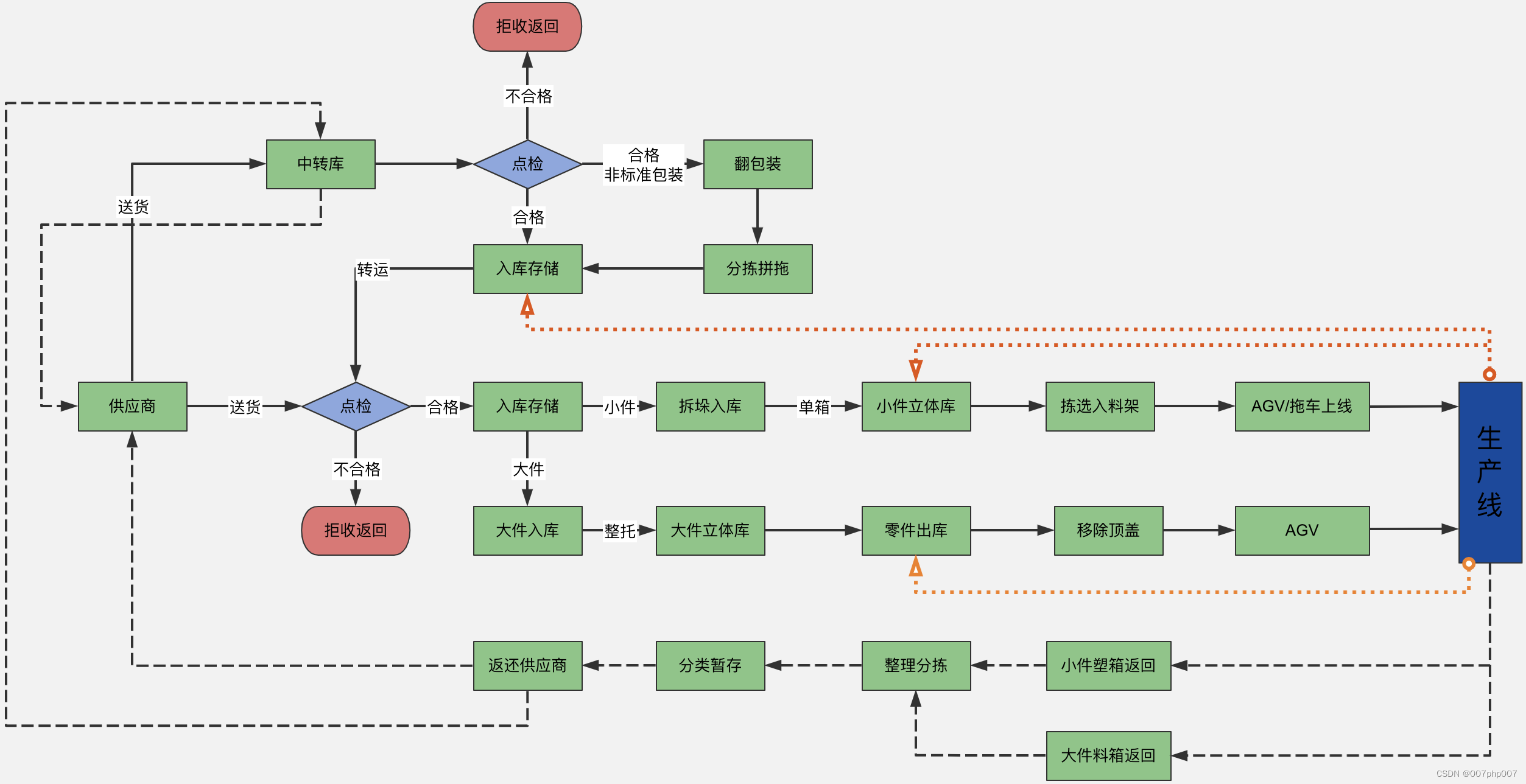
物流平台架构设计与实践
随着电商行业的迅猛发展,物流行业也得到了极大的发展。从最初的传统物流到现在的智慧物流,物流技术和模式也在不断的更新与升级。物流平台作为连接电商和物流的重要媒介,其架构设计和实践显得尤为重要。 一、物流平台架构设计 1. 前端架构设…...
RedHat8.4安装邮件服务器
一、配置发件服务器 1.1 根据现场IP,配置主机名 vim /etc/hosts 192.168.8.120 mail.test.com 将主机名更改为邮件服务器域名mail.test.com 1.2 关闭防火墙,禁止开机启动 systemctl stop firewalld systemctl disable firewalld 1.3 关闭selinux v…...

Linux Shell系列--dirname 去除基本文件名
一、目的 上一篇中我们介绍了basename命令的使用,本篇我们介绍dirname命令,dirname 命令与 basename 互补,它负责删除路径中的基本文件名部分(包括扩展名),只保留目录部分。 二、介绍 dirname首先去除字符…...
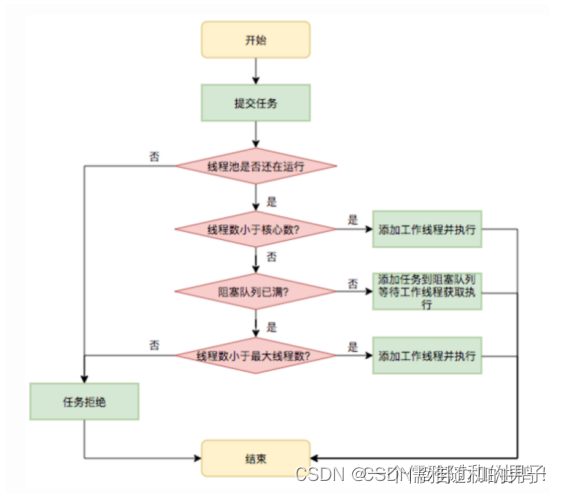
池化技术的总结
文章目录 1.什么是池化技术2.池化技术的应用一、连接池二、线程池三、内存池 3.池化技术的总结 1.什么是池化技术 池化技术指的是提前准备一些资源,在需要时可以重复使用这些预先准备的资源。 在系统开发过程中,我们经常会用到池化技术。通俗的讲&am…...
H5简约星空旋转引导页源码
H5简约星空旋转引导页源码 源码介绍:一款带有星空旋转背景特效的源码,带有四个按钮 下载地址: https://www.changyouzuhao.cn/11655.html...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...
