【教3妹学编程-算法题】1696. 跳跃游戏 VI

3妹:好冷啊, 冻得瑟瑟发抖啦
2哥 : 没想到都立春了还这么冷啊~
3妹:暴雪、冻雨、大雨,这天气还让不让人活啦!!!
2哥 :哎,好多人都滞留的高铁站了,没法回家了
3妹:我还不知道今天怎么回家呢,惨。
2哥:3妹,要不别回去了吧,我们就地过年
3妹:切,这里更冷,每天抖啊抖,跳啊跳才能缓解寒冷,我们家那儿可是有暖气的。
2哥:好吧,回家也也要记得每天刷题啊,刚好今天的题目是跳跃的, 让我们先做一下吧~

题目:
给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。
一开始你在下标 0 处。每一步,你最多可以往前跳 k 步,但你不能跳出数组的边界。也就是说,你可以从下标 i 跳到 [i + 1, min(n - 1, i + k)] 包含 两个端点的任意位置。
你的目标是到达数组最后一个位置(下标为 n - 1 ),你的 得分 为经过的所有数字之和。
请你返回你能得到的 最大得分 。
示例 1:
输入:nums = [1,-1,-2,4,-7,3], k = 2
输出:7
解释:你可以选择子序列 [1,-1,4,3] (上面加粗的数字),和为 7 。
示例 2:
输入:nums = [10,-5,-2,4,0,3], k = 3
输出:17
解释:你可以选择子序列 [10,4,3] (上面加粗数字),和为 17 。
示例 3:
输入:nums = [1,-5,-20,4,-1,3,-6,-3], k = 2
输出:0
提示:
1 <= nums.length, k <= 10^5
-10^4 <= nums[i] <= 10^4
思路:

动态规划 + 双端队列,
每一个位置的最大值取决于前面 k 步的最大得分,再加上当前位置的得分,由此我们想到可以使用动态规划来解决这个问题。
用 dp[i]来表示到达位置 i 的最大得分。初始状态 dp[0]=nums[0],表示位置 0的得分是它本身的得分。状态转移方程是
dp[i]=max{dp[j]}
其中 max(0,i−k)≤j<i。
其中前 k 步的最大值,使用优先队列可以达到 O(n×logn)的时间复杂度,使用双端队列可以达到 O(n)的时间复杂度。
java代码:
class Solution {public int maxResult(int[] nums, int k) {int n = nums.length;int[] dp = new int[n];dp[0] = nums[0];Deque<Integer> queue = new ArrayDeque<>();queue.offerLast(0);for (int i = 1; i < n; i++) {while (queue.peekFirst() < i - k) {queue.pollFirst();}dp[i] = dp[queue.peekFirst()] + nums[i];while (!queue.isEmpty() && dp[queue.peekLast()] <= dp[i]) {queue.pollLast();}queue.offerLast(i);}return dp[n - 1];}
}相关文章:

【教3妹学编程-算法题】1696. 跳跃游戏 VI
3妹:好冷啊, 冻得瑟瑟发抖啦 2哥 : 没想到都立春了还这么冷啊~ 3妹:暴雪、冻雨、大雨,这天气还让不让人活啦!!! 2哥 :哎,好多人都滞留的高铁站了,没法回家了 3妹…...

解决C#中无限递归导致的System.StackOverflowException异常
目录 背景: 错误示例分析: 为什么是错误的? 正确的使用递归: 修改后的代码: 原理和原因: 结论: 背景: 在软件开发中,递归是一种常见的编程技术,它允许方法调用自…...
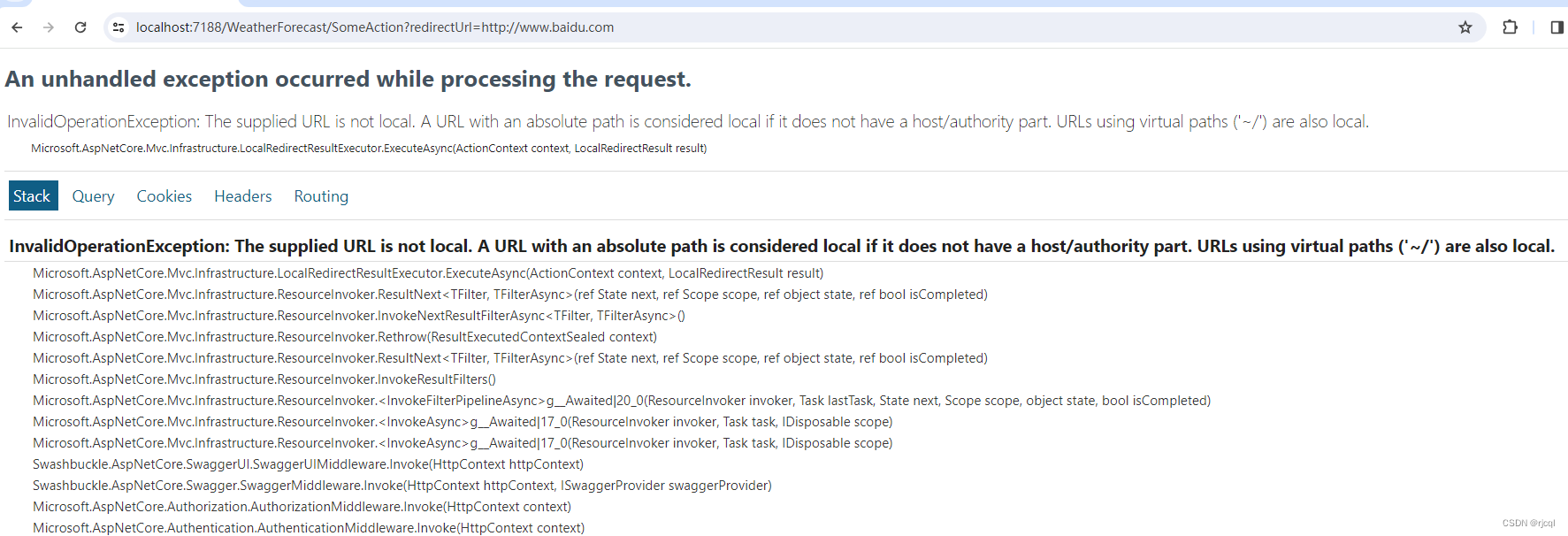
ASP.NET Core 预防开放式重定向攻击
写在前面 为预防钓鱼网站的常用套路,在进行 Web 应用程序的开发时,原则上应该将所有由用户提交的数据视为不可信。如果应用程序中包含了基于 URL 内容重定向的功能,需要确保这种类型的重定向操作只能在应用本地完成,或者明确判断…...

HashCat 恢复Excel、Word、PPT密码保姆教程
HashCat 恢复Excel、Word、PPT密码 一、流程 整体需要两个步骤 先用office2john.py获取下文件的hash值 python office2john.py 1.xlsx > hash这个命令需要你电脑有python环境,然后在cmd命令窗口中执行此命令就行 文件链接:https://github.com/magnu…...

flink实战--flink的job_listener使用解析
背景 生产环境可能有如下的需求:当一个flink作业提交完成或者是运行中不定时给我们触发某个接口或发送一个消息,然后我们在做其他的操作,尤其是batch作业。 flink的job_listener就可以满足我们监听flink任务提交和运行状态的需求,具体如何使用本文将全面介绍一下。 注册入…...

ASR 概述
前言 随着企业加强了与客户的线上沟通,企业越发依赖于虚拟助手、聊天机器人以及其他的语音技术,以实现与客户的高效互动。这几类人工智能,都是依赖于自动语音识别技术,简称为 ASR。ASR 涉及到将语音转换为文本,促使计…...
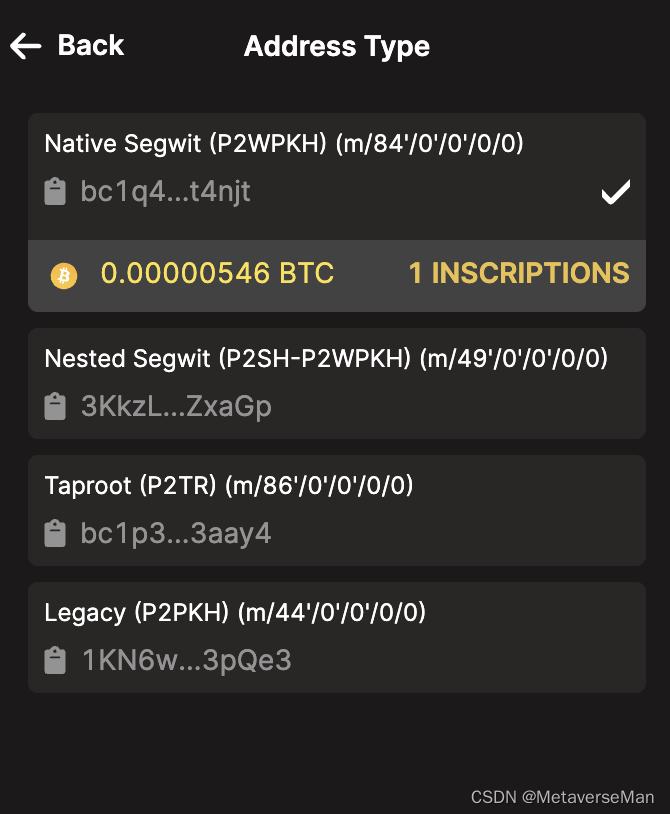
聊聊比特币----比特币地址
⽐特币地址是⼀个标识符(帐号),包含27-34个字母数字拉丁字符(0,O,I除外)。地址可以以QR码形式表⽰,是匿名的,不包含关于所有者的信息。 地址⽰例:14qViLJfdG…...
(4)【Python数据分析进阶】Machine-Learning模型与算法应用-回归、分类模型汇总
线性回归、逻辑回归算法应用请参考: https://codeknight.blog.csdn.net/article/details/135693621https://codeknight.blog.csdn.net/article/details/135693621本篇主要介绍决策树、随机森林、KNN、SVM、Bayes等有监督算法以及无监督的聚类算法和应用PCA对数据进行降维的算法…...

Python 调用 OpenAI ChatGPT API
一、安装环境1. 安装python环境 $ pip install openai 2. 验证是否安装成功 方法1,bash命令验证 $ pip show openai 方法2,python脚本验证 import openai print(openai.__version__) 3. 找到你的 OpenAI API Key:进入OpenAI官网࿰…...
springboot155基于JAVA语言的在线考试与学习交流网页平台
简介 【毕设源码推荐 javaweb 项目】基于springbootvue 的 适用于计算机类毕业设计,课程设计参考与学习用途。仅供学习参考, 不得用于商业或者非法用途,否则,一切后果请用户自负。 看运行截图看 第五章 第四章 获取资料方式 **项…...

echarts使用之地图(五)
1 基本使用 百度地图 API : 使用百度地图的 api , 它能够在线联网展示地图 , 百度地图需要申请 ak 矢量地图 : 可以离线展示地图 , 需要开发者准备矢量地图数据。本文使用该方式。 json格式的数据如下: 格式参照:GeoJSON <!DOCTYPE html&…...
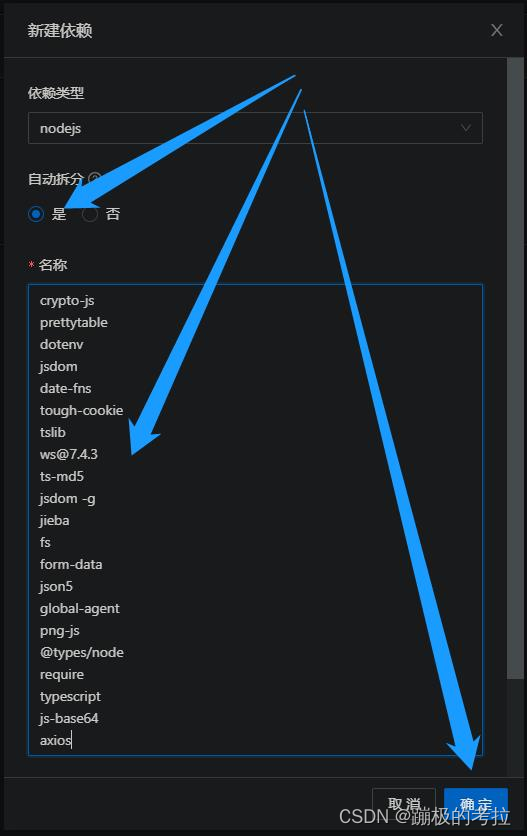
【已解决】青龙面板依赖安装失败原因
青龙面板必须安装依赖,才可以执行脚本,这是不争的事实。 如果脚本跑不起来,就去看看依赖吧。 NodeJs 依赖如下 axios request canvas cheerio js-base64 dotenv magic tough-cookie ws7.4.3 require requests date-fns ts-md5 typescript j…...
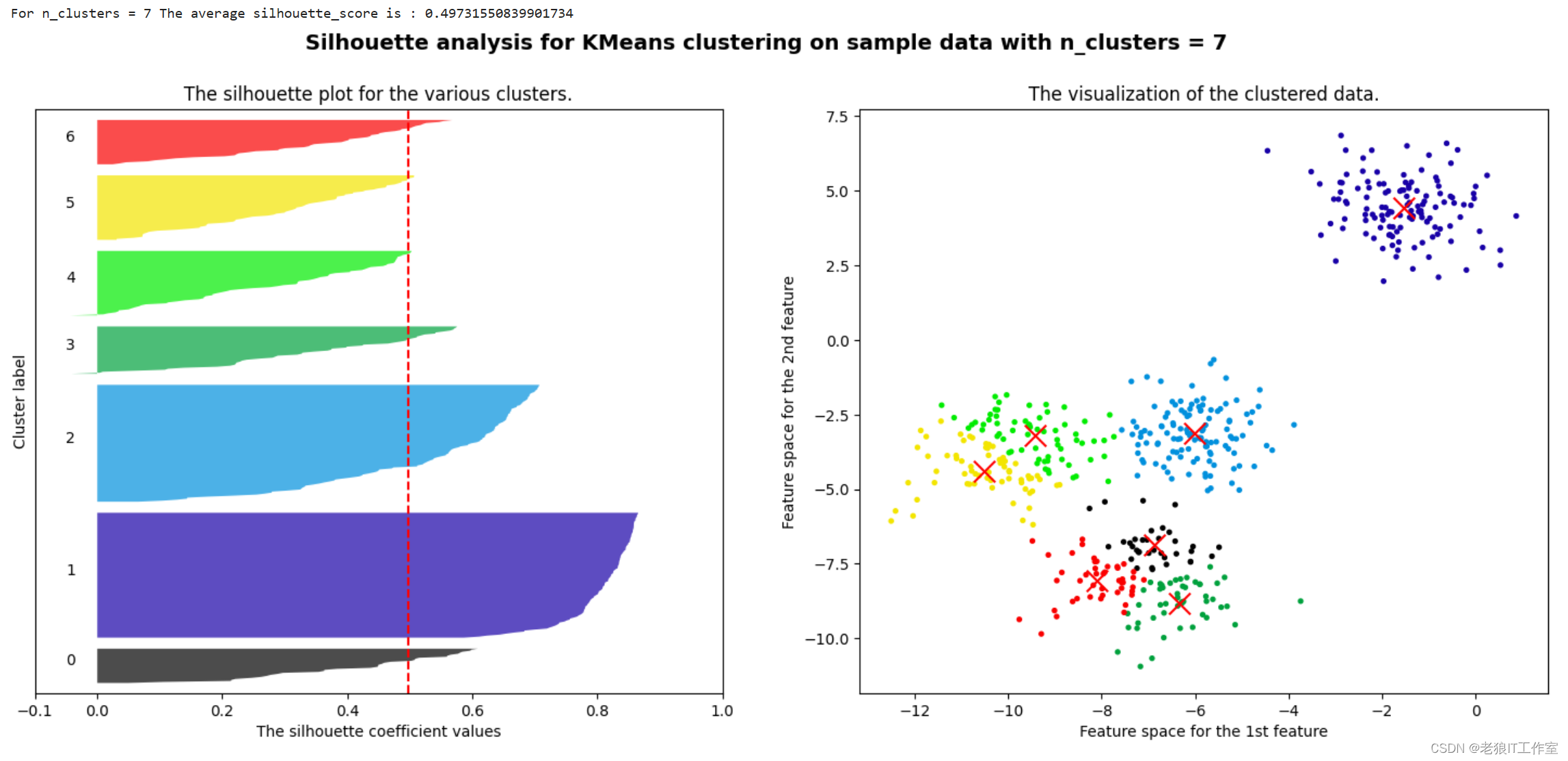
[Python] 什么是KMeans聚类算法以及scikit-learn中的KMeans使用案例
什么是无监督学习? 无监督学习是机器学习中的一种方法,其主要目的是从无标签的数据集中发现隐藏的模式、结构或者规律。在无监督学习中,算法不依赖于任何先验的标签信息,而是根据数据本身的特征和规律进行学习和推断。无监督学习…...
在 iOS 上安装自定企业级应用
了解如何安装您的组织创建的自定应用并为其建立信任。 本文适用于学校、企业或其他组织的系统管理员。 您的组织可以使用 Apple Developer Enterprise Program 创建和分发企业专用的 iOS 应用,以供内部使用。您必须先针对这些应用建立信任后,才能将其打…...

【Linux C | I/O模型】Unix / Linux系统的5种IO模型 | 图文详解
😁博客主页😁:🚀https://blog.csdn.net/wkd_007🚀 🤑博客内容🤑:🍭嵌入式开发、Linux、C语言、C、数据结构、音视频🍭 🤣本文内容🤣&a…...

C++设计模式-简单工厂模式,工厂方法模式,抽象工厂模式
目录 简单工厂模式,工厂方法模式,抽象工厂模式 附: 简单工厂模式,工厂方法模式,抽象工厂模式 简单工厂模式:根据字符串参数返回对象。 工厂方法模式:创建一维对象,即一个工厂创建…...

java处理ppt方案详解
需求 需要系统中展示的ppt案例有一个动态展示的效果,也就是要有动画的交互,要求支持浏览器直接打开预览 背景 目前已经实现了前端上传pptx文件,后端解析为png的图片,前端掉接口返回对应的图片,模拟播放ppt的效果 各种尝…...

鸿蒙4.0.0 安装minitouch
鸿蒙4.0.0 安装minitouch ubuntu 系统 minitouch 地址 https://github.com/DeviceFarmer/minitouch 因为 鸿蒙4.0.0 对应安卓12 API版本31 所以启动 minitouch 需要 STFService 地址 https://github.com/openstf/STFService.apk 到release下载最新的STFService.apk &…...
前端excel带样式导出 exceljs 插件的使用
本来用的xlsx和xlsx-style两个插件,过程一步一个坑,到完全能用要消灭好多bug。这时发现了exceljs,真香😀 案例 <!DOCTYPE html> <html><head><meta charset"utf-8" /><meta name"view…...

用GOGS搭建GIT服务器
GOGS官网 Gogs: A painless self-hosted Git service 进入文件所在目录 cd /usr/local/develop 解压文件 tar -xvf gogs_0.13.0_linux_amd64.tar.gz 解压之后 进入gogs 目录 cd gogs 创建几个目录 userdata 存放用户数据 log文件存放进程日志 repositories 仓库根目…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...
