Verilog实现2进制码与BCD码的互相转换
1、什么是BCD码?
BCD码是一种2进制的数字编码形式,用4位2进制数来表示1位10进制中的0~9这10个数。这种编码技术,最常用于会计系统的设计里,因为会计制度经常需要对很长的数字做准确的计算。相对于一般的浮点式记数法,采用BCD码,既可保存数值的精确度,又可使电脑免除作浮点运算所耗费的时间。此外,对于其他需要高精确度的计算,BCD编码也很常用。
常见的BCD码有很多种形式,比如8421码、2421码、5421码、余3码等等,其中最常用的是8421码,接下来的讨论都建立在8421BCD码的基础上。
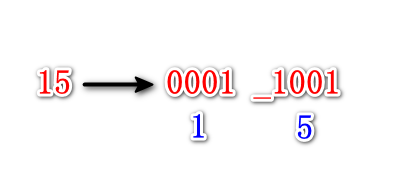
BCD码的一个很大的优势是可以很方便的用2进制来显示10进制数。比如10进制数15如果用2进制存储,就是1111,也就是16进制的F,如果它显示在数码管上是“F”,但是这种显示方式对我们来说其实并不友好,我们更习惯地还是“1 5”。

而BCD码存储10进制数15,则需要8位,高4位存储十位“1”,低四位存储个位“5”,也就是“0001”和“1001”,这样就可以做到把“1”和“5”这两个数字分别显示了:
BCD码的一般形式如下:
| 十进制数 | BCD码 |
|---|---|
| 0 | 0 0 0 0 |
| 1 | 0 0 0 1 |
| 2 | 0 0 1 0 |
| 3 | 0 0 1 1 |
| 4 | 0 1 0 0 |
| 5 | 0 1 0 1 |
| 6 | 0 1 1 0 |
| 7 | 0 1 1 1 |
| 8 | 1 0 0 0 |
| 9 | 1 0 0 1 |
2、2进制码转BCD码
如何将2进制码转换为BCD码?4位的转换相对简单,只要根据数值的大小加6就可以了。因为4位二进制码可以表示0-15这16个数,而BCD码只能表示0-9这10个数。也就是说4位2进制数逢16进位,而4位BCD逢10进位,所以需要加6这个差值来给它人工进位。比如4位2进制数1111(10进制15),加上6后,为1111+1010 = 1_1001,高位可以视作补齐3个0,即0001_1001,0001表示1,1001表示5。
2.1、除法和取模
加6修正法只适用于4位的转换,位数高了以后,这个方法就不适用了。比如1_1111(F)加上6后,显然就没用。
多位数的2进制码转BCD码有一种很容易想到的办法:利用除法和取模。比如8位2进制数可以表示的范围是0~255,那么就可以用3个4bit数来分别表示个位、十位和百位。以255为例:
个位 = 255%10 = 5;
十位 = 255% 100 / 10 = 55/10 = 5;
百位 = 255/100 = 2;
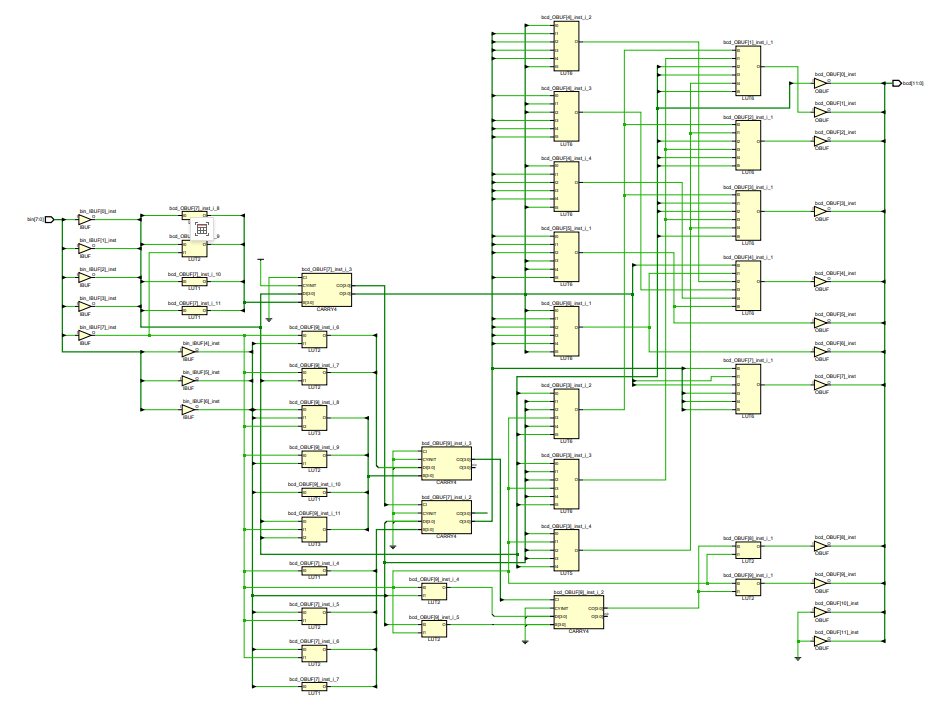
这种方法在逻辑上理解起来非常简单,但是有个很大的缺点就是涉及到了除法和取模操作。众所周知,用FPGA做除法和取模操作将消耗大量的逻辑资源,而且时序也容易跑不高。下面是这种方法的RTL:
`timescale 1 ns/1 ns
module test(input [7 :0] bin,output [11:0] bcd
);wire [3:0] ones,tens,huns; assign ones = bin % 10;
assign tens = bin % 100 / 10;
assign huns = bin / 100;
assign bcd = {huns,tens,ones};endmodule
这样综合出来的电路确实面积不小,一共用了27个LUT,逻辑级数5级:
编写Testbench对电路进行测试:
`timescale 1 ns/1 ns
module tb_test;reg [7:0] bin;
wire [11:0] bcd;integer i,j;
reg [8:0] err; //错误计数器
reg [11:0] bcd_true[0:255]; //进行对比的正确输出//例化被测试模块
test u_test (.bin (bin), .bcd (bcd)
);//生成做对比的正确输出
initial beginfor(j=0;j<256;j=j+1)beginbcd_true[j][3 :0] = j % 10;bcd_true[j][7 :4] = j % 100 / 10;bcd_true[j][11:8] = j / 100;end
end//生成测试激励
initial beginerr = 0;for(i=0;i<256;i=i+1)beginbin = i; #10; if(bcd_true[bin] != bcd )begin //如果转换有误$display("%3d is Wrong!",bin); //打印错误输入err = err + 1; //统计错误个数end end $display("Test Complete!%3d errs!",err);//打印结束仿真信息,并输出错误个数$stop; //结束仿真
endendmodule
这个TB文件添加了自动对比机制,所以我们只需要关注窗口打印的信息:

稍微看下波形也可以知道,仿真结果是没问题的(bin是10进制显示,bcd是16进制显示):

2.2、查找表法
位数不多的情况下还有一种更简单的方法–查找表法。查找表法的原理很简单,把所有输入所对应的输出都放到一个ROM里边存起来,然后通过地址寻址方式来取值就行了。比如5位2进制数的转换则只需要储存0~31这32个数值就行,8位2进制数也只需要存储256个数值。
下面是用查找表法写的8位2进制数转BCD的代码,需要注意的是,由于篇幅过长,省去了部分代码,而且为了有对比,故意把最后两个数即8‘d254和8‘d255的输出弄成了错误输出。
module test(input [7:0] bin,output reg [11:0] bcd
);always @(*)begincase(bin)8'd 0:bcd=12'b000000000000;8'd 1:bcd=12'b000000000001;8'd 2:bcd=12'b000000000010;//这里开始省略了很多次赋值8'd254:bcd=12'b001001010000; //这里是故意弄错了8'd255:bcd=12'b001001010001; //这里是故意弄错了 default:bcd=12'b000000000000;endcase
end endmodule
除了采用case语句赋值的方式外,还有很多其他实现查找表的方式,比如例化ROM,或者用综合属性执行生成DRAM等。这样综合出来的电路结构用了13个LUT+4个MUX,比起之前的方法(27个LUT)少用了很多资源。
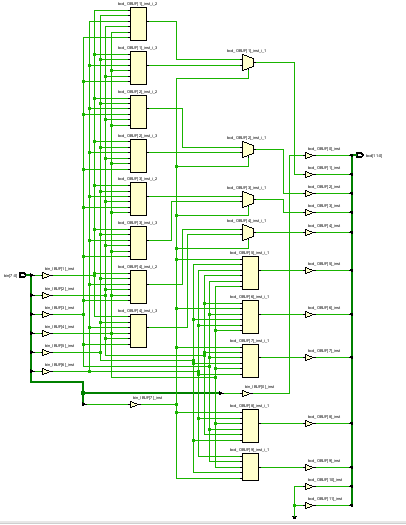
仿真用同样的TB就行,这是仿真结果:

因为之前故意把8‘d254和8‘d255这两个数弄错了,所以这里检测到了并打印了出来,其他仿真结果无误。
2.3、Double dabble(移位加3法)
4位二进制大于15才进位,而BCD码是大于9就进位,若4位二进制大于9时进位,这样得到的就是15的BCD码,因此将大于9的四位二进制数加6就能得到其BCD码。对于大于四位的二进制数,通过左移,逢9加6进位,即可转换任意位的二进制数,比如说,对于5位二进制数,由高4位二进制数左移一位得到,那么将前4位得到的BCD码也左移一位,并重新判断低四位是否大于4,若大于4,则加3进位,即可得到5位二进制数对应的BCD码。这种算法叫Double dabble,中文叫移位加3法。
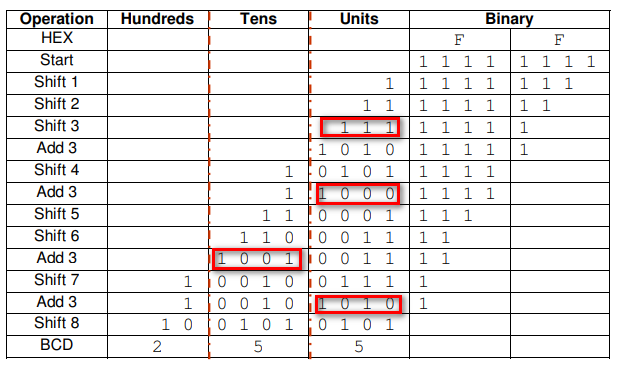
上图展示了这种方法的详细过程,二进制数1111_1111(10进制数255)从高位开始依次向左移位,移入到3个4bit组成的12位寄存器了,然后判断每个4bit是否大于4,若是则+3修正,然后继续移位。判断大于4是因为左移相当于乘以2,实际上就是在判断是否大于10产生了进位,而+3经过左移后会变成+6,同样是对2进制与BCD不同位进位所进行的修正。
所以这一过程是:从高位开始移位>>判断每个4bit是否大于4,若是则加3>>重复操作,直到所有位都被移出。
下面以8位2进制数转BCD为例,它的过程应该是这样的:

在这个电路中,Adder模块实现输入大于4就加3进位的功能
0和高3位构成左移3次后的低四位,经过Adder1模块后,得到调整后的数据
其他位类推
最后,在高位填0并与最低位的a0构成最终左移八次的十二位数据
首先设计大于4就加3模块:
//如果大于4就+3
module add3_g4(input [3 : 0] in,output reg [3 : 0] out
);//利用查找表实现+3操作
always @ (*) begincase (in) 4'b0000 : out = 4'b0000;4'b0001 : out = 4'b0001;4'b0010 : out = 4'b0010;4'b0011 : out = 4'b0011;4'b0100 : out = 4'b0100;4'b0101 : out = 4'b1000;4'b0110 : out = 4'b1001;4'b0111 : out = 4'b1010;4'b1000 : out = 4'b1011;4'b1001 : out = 4'b1100;default : out = 4'b0000;endcase
end
endmodule
然后是主模块(其实就是模块化设计方法,简称连连看)
module test(input [7:0] bin,output [11:0] bcd
);wire [3 : 0] t1, t2, t3, t4, t5, t6, t7;add3_g4 adder1(.in ({1'b0, bin[7 : 5]}),.out(t1[3 : 0])
);
add3_g4 adder2(.in ({t1[2 : 0], bin[4]}),.out(t2[3 : 0])
);
add3_g4 adder3(.in({t2[2 : 0], bin[3]}),.out(t3[3 : 0])
);
add3_g4 adder4(.in({1'b0, t1[3], t2[3], t3[3]}),.out(t4[3 : 0])
);
add3_g4 adder5(.in({t3[2 : 0], bin[2]}),.out(t5[3 : 0])
);
add3_g4 adder6(.in({t4[2 : 0], t5[3]}),.out(t6[3 : 0])
);
add3_g4 adder7(.in({t5[2 : 0], bin[1]}),.out(t7[3 : 0])
);assign bcd = {2'b0, t4[3], t6[3 : 0], t7[3 : 0], bin[0]};endmodule
这种方法综合出来只用了10个LUT,资源消耗甚至比查找表法还少。
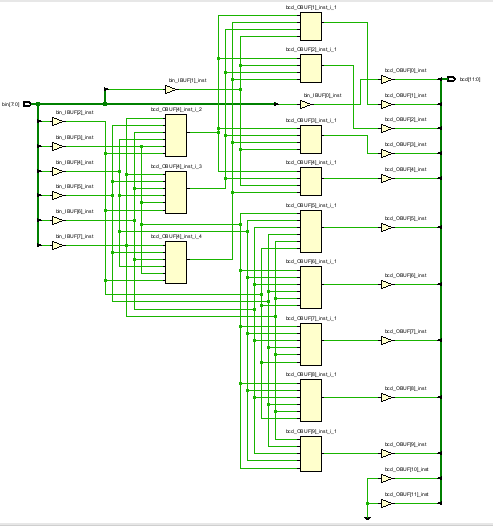
再用同样的TB仿真,仿真结果表明这个设计没问题:
这种模块化的设计方法有2个很不好的地方
- 不够抽象,需要把图画出来才能理解
- 几乎没有可拓展性,如果改变位数则RTL需要大改
所以接下来,设计一个位宽可变的、抽象程度更高的电路:
module test
#( parameter W = 8 //输入位宽可变
)
( input [W-1 :0] bin, output reg [W+(W-4)/3:0] bcd
); integer i,j; //循环参数always @(*) beginfor(i = 0; i <= W+(W-4)/3; i = i+1) bcd[i] = 0; //用全0初始化bcd[W-1:0] = bin; //低位用输入替换for(i = 0; i <= W-4; i = i+1) for(j = 0; j <= i/3; j = j+1) if (bcd[W-i+4*j -: 4] > 4) //如果大于4bcd[W-i+4*j -: 4] = bcd[W-i+4*j -: 4] + 4'd3; //+3
endendmodule
这样综合出来的电路面积也很小,只用了11个LUT:

使用这个模块的时候需要注意的一点是,它的输出参数化设计是设计得最小的模块。比如8位2进制数最大为255,实际上用10个bit的BCD码就可以表示,但是我们一般习惯用12个bit来表示,所以可以在最后的结果前面补0。
2.4、使用资源对比
将输入位数扩大到16位2进制数的转换,再分别使用3个方法构建电路,观察资源消耗情况:
| 除法和取模 | 查找表 | 移位加3 |
|---|---|---|
| 287个LUT | 23220个LUT或者36个BRAM | 71个LUT |
可以看到随着输入位数的增加,移位加3法的优势就更明显。一般来讲。查找表法适合位数不多的情况;而直接用除法则非常省事,适合对资源消耗和时序都没什么要求的时候使用。
3、BCD码转2进制码
了解了如何从2进制码转BCD码后,那么从BCD码转2进制码的方法就简单了–无非就是上述方法的逆过程嘛!
3.1、查找表
这个没什么好说的,和2进制码转BCD码的流程一模一样,只是ROM里面的存储内容不同罢了。
3.2、乘法(直接乘法与移位加法)
以12位BCD码255为例,若转换成2进制码,则只需要8bit。最高位的2可以看做百位,中间的5可以看做十位,最低位的5可以看做个位,所以转换后应该是2*100+5*10+5=255(10进制)=1111_1111(2进制)。只用乘法就可以实现BCD码转2进制码,由于乘法可以转换成移位和加法,所以消耗的资源也不会特别多。
下面是直接用乘法来实现20位BCD转16位BIN的RTL:
//乘法:20位BCD转16位BIN,加上时钟,49lut+24carry4
//slak=2.381ns,观察FMAX = 131Mhz,逻辑级数8
module test(input clk,input [19:0] bcd,output reg [15:0] bin
);wire [3:0] ten_thos; //10000
wire [3:0] thos; //1000
wire [3:0] huns; //100
wire [3:0] tens; //10
wire [3:0] ones; //1wire [19:0] ten_thos_shift;
wire [19:0] thos_shift;
wire [19:0] huns_shift;
wire [19:0] tens_shift; reg [19:0] bcd_r;always @(posedge clk) //输入寄存一拍bcd_r <= bcd;
always @(posedge clk) //输出寄存一拍 bin <= ten_thos_shift + thos_shift+ huns_shift + tens_shift + ones; assign ten_thos = bcd_r[19:16];
assign thos = bcd_r[15:12];
assign huns = bcd_r[11:8];
assign tens = bcd_r[7 :4];
assign ones = bcd_r[3 :0]; assign ten_thos_shift = ten_thos*10000;
assign thos_shift = thos*1000;
assign huns_shift = huns*100;
assign tens_shift = tens*10;endmodule
这样综合出来的电路一共消耗49个LUT+24个CARRY4,最大逻辑级数为8,Fmax约为131Mhz。

用移位和加法来实现乘法:
//移位加法实现乘法,加上时钟,53 lut+ 13 carry4
//slack5.517ns,观察FMAX = 223Mhz,逻辑级数7
module test(input clk,input [19:0] bcd,output reg [15:0] bin
);wire [3:0] ten_thos; //10000
wire [3:0] thos; //1000
wire [3:0] huns; //100
wire [3:0] tens; //10
wire [3:0] ones; //1wire [19:0] ten_thos_shift;
wire [19:0] thos_shift;
wire [19:0] huns_shift;
wire [19:0] tens_shift; reg [19:0] bcd_r;always @(posedge clk) //输入寄存一拍bcd_r <= bcd;
always @(posedge clk) //输出寄存一拍 bin <= ten_thos_shift + thos_shift+ huns_shift + tens_shift + ones; assign ten_thos = bcd_r[19:16];
assign thos = bcd_r[15:12];
assign huns = bcd_r[11:8];
assign tens = bcd_r[7 :4];
assign ones = bcd_r[3 :0]; //移位后的万位=1*10000=1*(8192+1024+512+256+16)
assign ten_thos_shift = (ten_thos<<13) + (ten_thos<<10) + (ten_thos<<9) + (ten_thos<<8) + (ten_thos<<4);
//移位后的千位=1*1000=1*(1024-16-8)
assign thos_shift = (thos<<10) - (thos<<4) - (thos<<3);
//移位后的百位=1*100=1*(64+32+4)
assign huns_shift = (huns<<6) + (huns<<5) + (huns<<2);
//移位后的十位=1*10=1*(8+2)
assign tens_shift = (tens<<3) + (tens<<1);endmodule
这样综合出来的电路一共消耗53个LUT+13个CARRY4,最大逻辑级数为7,Fmax为223Mhz,电路性能是比直接用乘法要好的。

3.3、移位减3法
移位加3法的逆过程自然就是移位减3发,但是注意判断条件–BCD码逢十进一,四位二进制逢十六进一,所以转二进制的条件即为16/2=8(右移),即需要判断每个BCD码的4位是否大于等于8,同时向右移位到二进制码中。
下面展示了BCD码0010_0100_0011到2进制码1111_0011的过程。
BCD Input Binary Output2 4 30010 0100 0011 00000000 初始化0001 0010 0001 10000000 向右移位0000 1001 0000 11000000 向右移位0000 0110 0000 11000000 中间4位值为9,所以要-30000 0011 0000 01100000 向右移位0000 0001 1000 00110000 向右移位0000 0001 0101 00110000 最右4位值为8,所以要-30000 0000 1010 10011000 向右移位0000 0000 0111 10011000 最右4位值为10,所以要-30000 0000 0011 11001100 向右移位0000 0000 0001 11100110 向右移位0000 0000 0000 11110011 向右移位
下面的RTL实现了12位BCD码转8位2进制码:
module test
( input [11:0] bcd, output reg [7 :0] bin
); integer i,j; //循环参数
reg [11:0] temp;always @(*) begintemp[11:0] = bcd; //用输入替换for(i = 1; i <= 7; i = i+1) begin for(j = 0; j <= (7-i)/4; j = j+1) begin if (temp[i+4*j +: 4]>=8)begin // if > 4temp[i+4*j +: 4] = temp[i+4*j +: 4] - 4'd3; //-3endend end bin= temp;
endendmodule
这样综合出来的电路一共消耗17个LUT,最大逻辑级数为3,Fmax为323Mhz。

下面是20位BCD转16位BIN的RTL:
module test
(input [19:0] bcd, output reg [15:0] bin
); integer i,j; //循环参数
reg [19:0] temp; always @(*) begintemp = bcd; //输入替换for(i = 1; i <= 15; i = i+1) begin //16-1 for(j = 0; j <= (15-i)/4; j = j+1) begin if (temp[i+4*j +: 4]>=8)begin // if > 4temp[i+4*j +: 4] = temp[i+4*j +: 4] - 4'd3; //+3endend end bin= temp;
endendmodule
3.4、资源及时序对比
将输入位数扩大到20位BCD转16位2进制数的转换,再分别使用3个方法构建电路,观察资源消耗情况:
| 直接乘 | 移位+加法 | 查找表 | 移位-3法 |
|---|---|---|---|
| 49个LUT+24个CARRY4 | 53 lut+ 13 carry4 | 23220个LUT或者36个BRAM | 71个LUT |
| FMAX = 131Mhz,逻辑级数8 | FMAX = 223Mhz,逻辑级数7 | / | FMAX = 147Mhz,逻辑级数7 |
移位减3法和直接乘法的资源消耗以及速度都差不多,这是因为乘法容易乘转换成移位+加法,这是FPGA很容易实现的形式,并不会像除法和取模那样消耗非常多的资源。用移位+加法来实现乘法的形式的资源消耗和时序性能是最好的,所以BCD转2进制数,建议用左移+加法来实现乘法。
4、总结
- 位数不多的情况下,BCD码与2进制码的互转用查找表法都是最好的实现形式
- 位数较多的情况下,2进制码转BCD码更推荐用移位加3法;BCD码转2进制码更推荐用移位+加法来实现乘法的形式
------------ | ---------------------- | ----------------------- |
| 49个LUT+24个CARRY4 | 53 lut+ 13 carry4 | 23220个LUT或者36个BRAM | 71个LUT |
| FMAX = 131Mhz,逻辑级数8 | FMAX = 223Mhz,逻辑级数7 | / | FMAX = 147Mhz,逻辑级数7 |
移位减3法和直接乘法的资源消耗以及速度都差不多,这是因为乘法容易乘转换成移位+加法,这是FPGA很容易实现的形式,并不会像除法和取模那样消耗非常多的资源。用移位+加法来实现乘法的形式的资源消耗和时序性能是最好的,所以BCD转2进制数,建议用左移+加法来实现乘法。
4、总结
- 位数不多的情况下,BCD码与2进制码的互转用查找表法都是最好的实现形式
- 位数较多的情况下,2进制码转BCD码更推荐用移位加3法;BCD码转2进制码更推荐用移位+加法来实现乘法的形式
- 📣您有任何问题,都可以在评论区和我交流📃!
- 📣本文由 孤独的单刀 原创,首发于CSDN平台🐵,博客主页:wuzhikai.blog.csdn.net
- 📣您的支持是我持续创作的最大动力!如果本文对您有帮助,还请多多点赞👍、评论💬和收藏⭐!
相关文章:

Verilog实现2进制码与BCD码的互相转换
1、什么是BCD码? BCD码是一种2进制的数字编码形式,用4位2进制数来表示1位10进制中的0~9这10个数。这种编码技术,最常用于会计系统的设计里,因为会计制度经常需要对很长的数字做准确的计算。相对于一般的浮点式记数法,…...
 C. Jellyfish and Green Apple (思维))
Codeforces Round 901 (Div. 2) C. Jellyfish and Green Apple (思维)
题目链接 代码 (判空): #include<bits/stdc.h> using namespace std; #define endl "\n" typedef long long ll; typedef pair<int, int> PII; typedef pair<PII, int> PIII; const int inf 0x3f3f3f3f; const ll infinf 0x3f3f3f3f3f3f3f3f;/…...
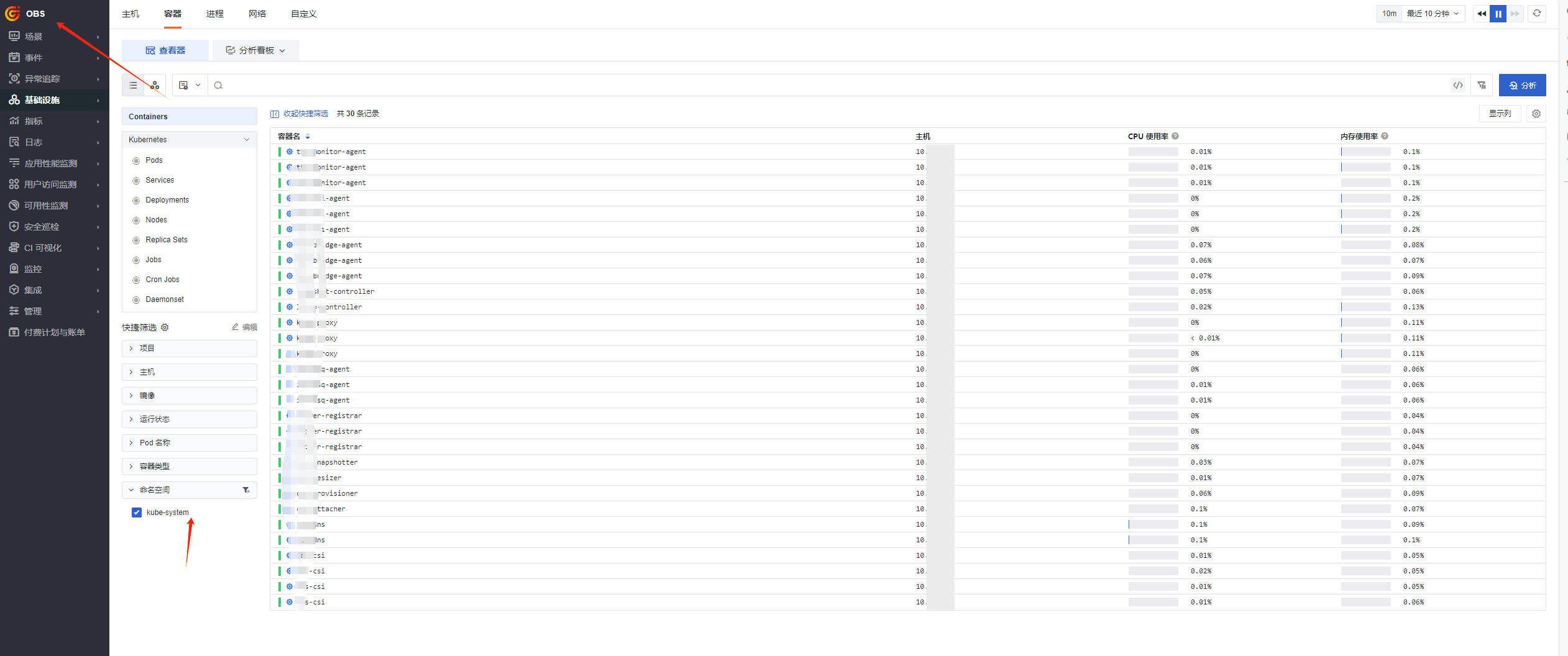
K8s 集群可观测性-数据分流最佳实践
简介 在微服务架构下,一个 k8s 集群中经常会部署多套业务,同时也意味着不同团队、不同角色、不同的业务会在同一集群中,需要将不同业务的数据在不同的空间进行管理和查看。 在传统的主机环境下,这个是可以通过不同的主机部署 Da…...
muduo库的模拟实现——工具部分
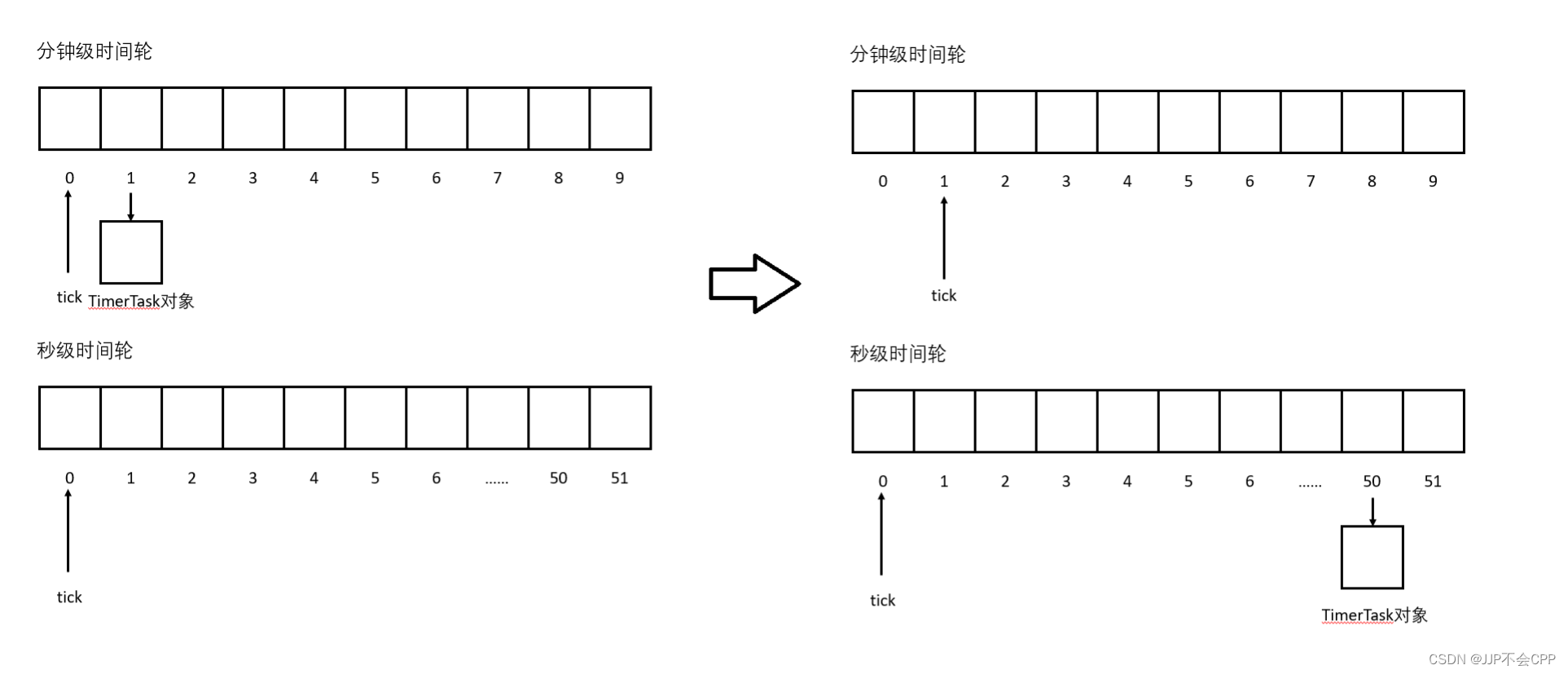
文章目录 一、Buffer模块1.为什么需要Buffer缓冲区2.Buffer模块的设计3.Buffer模块的实现4.Buffer缓冲区的其它设计方案 二、Socket模块1.Socket模块的设计2.Socket代码实现 三、Acceptor模块1.Acceptor模块的设计与实现2.Acceptor模块完整代码实现 四、定时器模块1.时间轮的思…...
SpringBoot接入微信公众号【服务号】
SpringBoot接入微信公众号【服务号】 一、服务号注册 注册地址:https://mp.weixin.qq.com/cgi-bin/registermidpage?actionindex&langzh_CN 注册流程参考:https://kf.qq.com/touch/faq/150804UVr222150804quq6B7.html?platform15 二、服务号配…...
2023 英特尔On技术创新大会直播 |探索视觉AI的无限可能
2023 英特尔On技术创新大会直播 | 探索视觉AI的无限可能 前言一未来的 AI:释放视觉 AI 真正潜力二AI技术突破、视觉Al挑战及前沿研究创新三全尺度视觉学习全尺度视觉学习示例1.GridConv 实现三维人体姿态估计更高准确率2.KW 预训练及迁移模型性能3.无数据增强稠密对…...
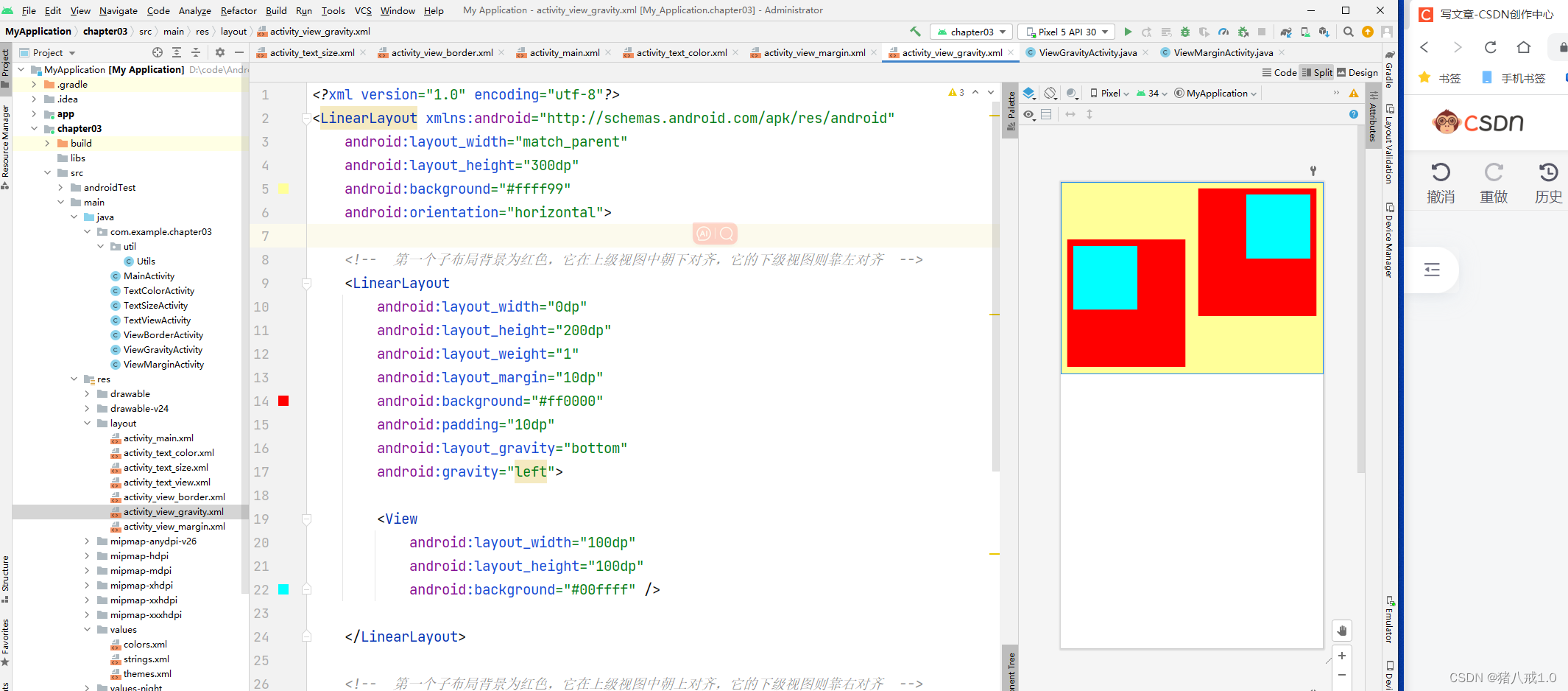
安卓视图基础
目录 设置视图的宽高 设置视图的间隔 设置视图的对齐方式 设置视图的宽高 设置视图的间隔 设置视图的对齐方式 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas.android.com/apk/res/android"a…...
电路设计(10)——超温报警电路的proteus仿真
1.题目背景 在现实生活中,常有一种工程技术,即带有自动温度补偿的设备,能在规定温度内正常工作。但是为了设备安全,需设定工作的上限温度,万一温控补偿失效,设备温度一旦超出上限温度时,便立即切…...
 | gerrit 简介)
gerrit(1) | gerrit 简介
gerrit(1) | gerrit 简介 1. 目的 之前用过 gitlab CI/CD, github actions, 以及公司的配置管理员配置的 jenkins。 github 的 MR, github 的 PR, 虽然在用, 但仅限于参与开源项目或公司内的开源项目, OEM 项目中完全没在用。 …...

计算机视觉实战项目3(图像分类+目标检测+目标跟踪+姿态识别+车道线识别+车牌识别+无人机检测+A*路径规划+单目测距与测速+行人车辆计数等)
车辆跟踪及测距 该项目一个基于深度学习和目标跟踪算法的项目,主要用于实现视频中的目标检测和跟踪。该项目使用了 YOLOv5目标检测算法和 DeepSORT 目标跟踪算法,以及一些辅助工具和库,可以帮助用户快速地在本地或者云端上实现视频目标检测和…...

redis(5)
文章目录 一、redis 哨兵(sentinel)redis 集群介绍哨兵(Sentinel)工作原理sentinel 架构和故障转移sentinel中的三个定时任务 实时哨兵启动哨兵验证哨兵端口查看哨兵日志当前sentinel状态停止Redis Master测试故障转移恢复故障的m…...
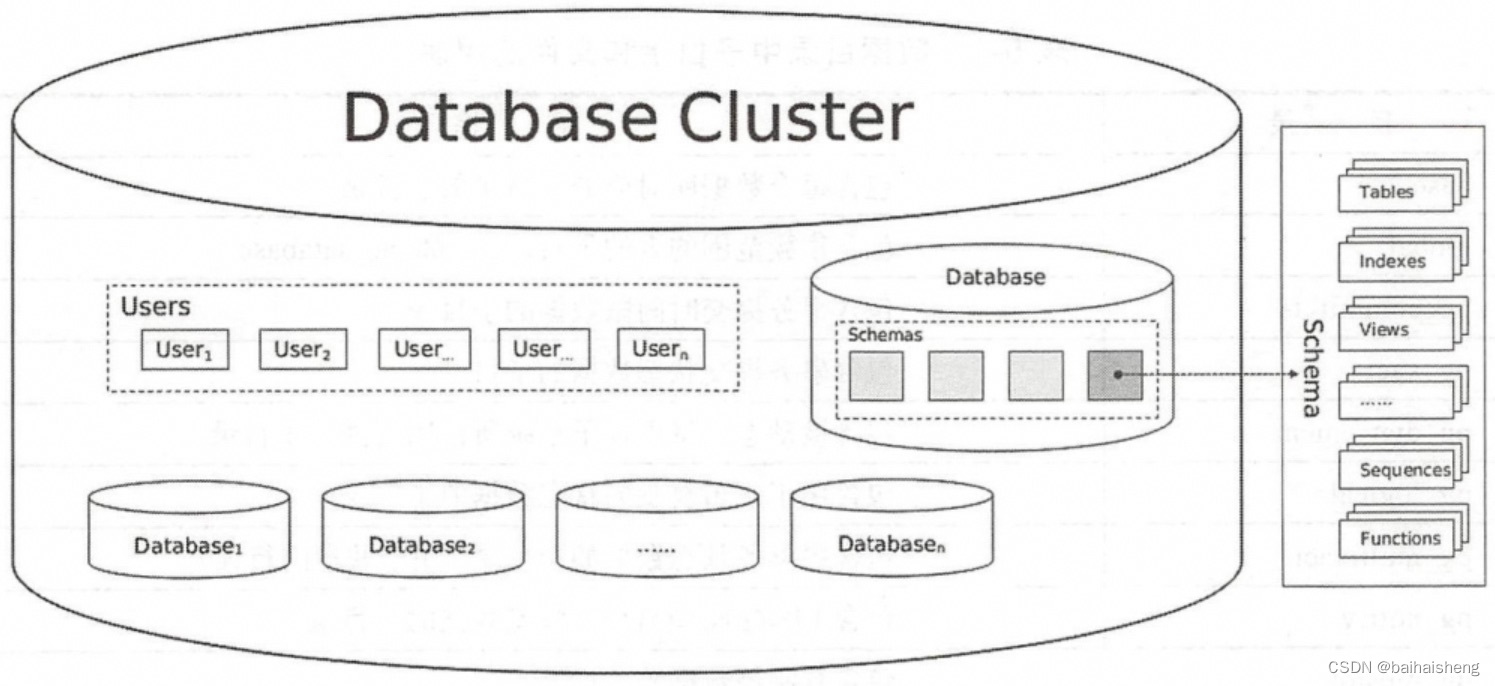
Postgresql体系结构
client连接PostgreSQL过程: 1、客户端发起请求 2、主服务postmaster进程负责服务器是否接受客户端的host通信认证,服务器对客户端进行身份鉴别 3、主服务进程为该客户端单独fork一个客户端工作进程postgres 4、客户端与postgres进程建立通信连接…...

【Rust】——rust前言与安装rust
🎃个人专栏: 🐬 算法设计与分析:算法设计与分析_IT闫的博客-CSDN博客 🐳Java基础:Java基础_IT闫的博客-CSDN博客 🐋c语言:c语言_IT闫的博客-CSDN博客 🐟MySQL:…...
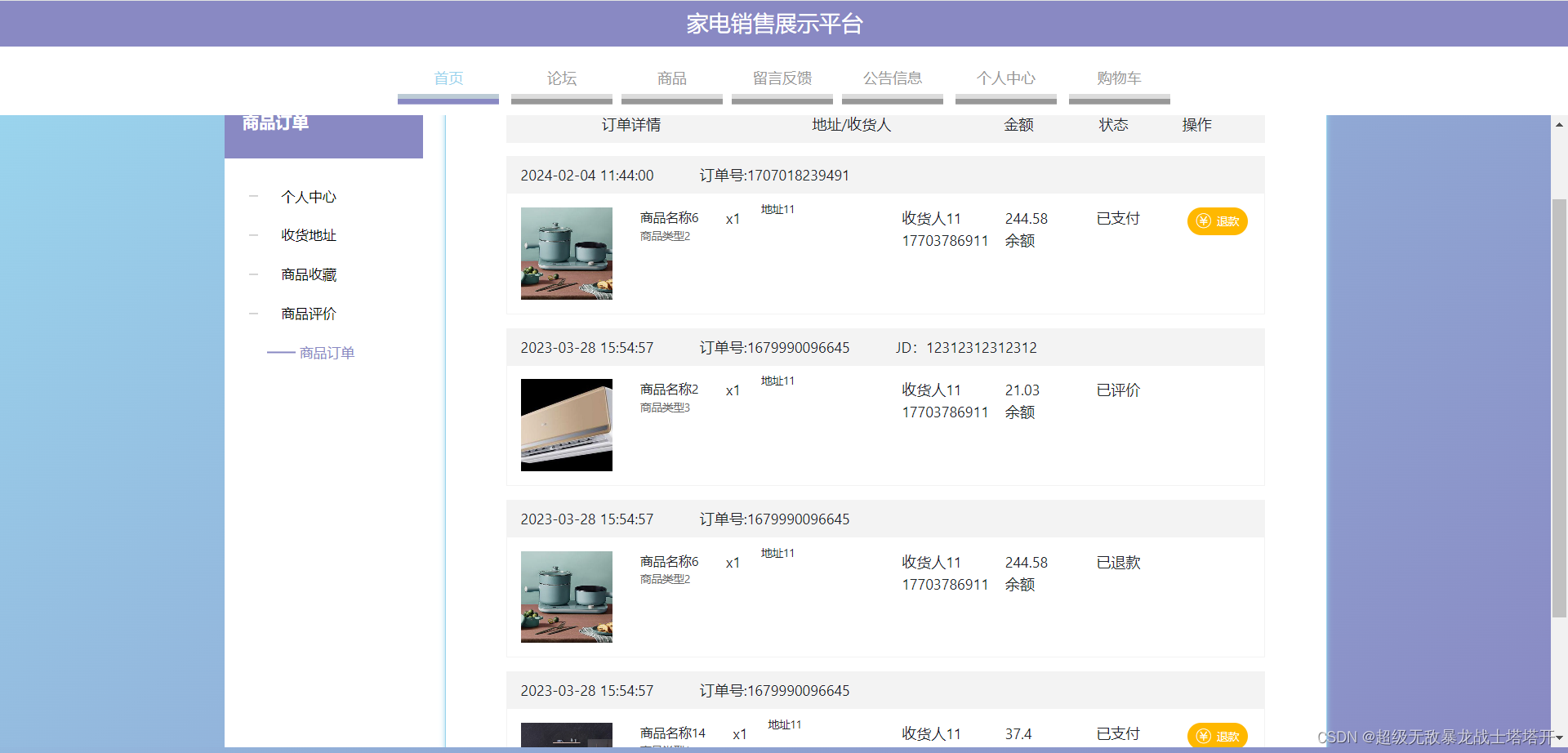
基于SpringBoot的家电销售展示网页的设计与实现
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式 🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 &…...
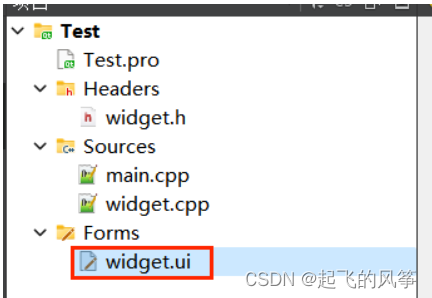
【Qt】—— 项⽬⽂件解析
目录 (一).pro⽂件解析 (二)widget.h⽂件解析 (三)main.cpp⽂件解析 (四)widget.cpp⽂件解析 (五)widget.ui⽂件解析 (一).pro⽂…...
【Linux】静态库和动态库
动静态库 一、静态库1. 静态库概念2. 制作静态库(1)朴素方法 --- 不打包(2)对静态库打包 3. 使用静态库(1)朴素方法 --- 直接使用(2)使用打包好的静态库 二、动态库1. 动态库概念2. …...

LeetCode 0292.Nim 游戏:脑筋急转弯
【LetMeFly】292.Nim 游戏:脑筋急转弯 力扣题目链接:https://leetcode.cn/problems/nim-game/ 你和你的朋友,两个人一起玩 Nim 游戏: 桌子上有一堆石头。你们轮流进行自己的回合, 你作为先手 。每一回合,…...
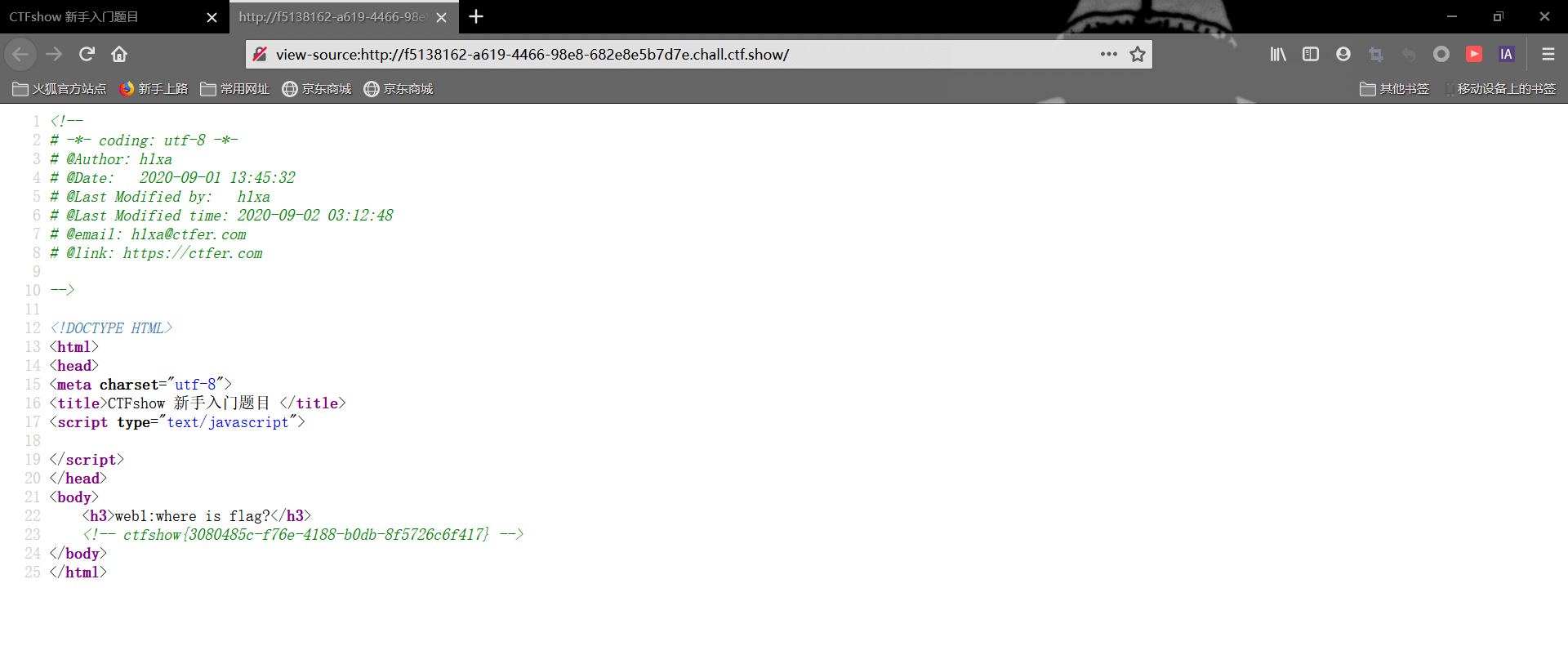
ctfshow-web1~10-WP
web1 右键查看源码就能看到flag web2 打开网页提示无法查看源代码,右键也使用不了,那我们就在url前面加上view-source: view-source:http://83a83588-671e-4a94-9c6f-6857f9e20c2f.chall.ctf.show/ 访问后即可获得flag web3 右键源码也没看到信息,去查看一下请求头和响应…...
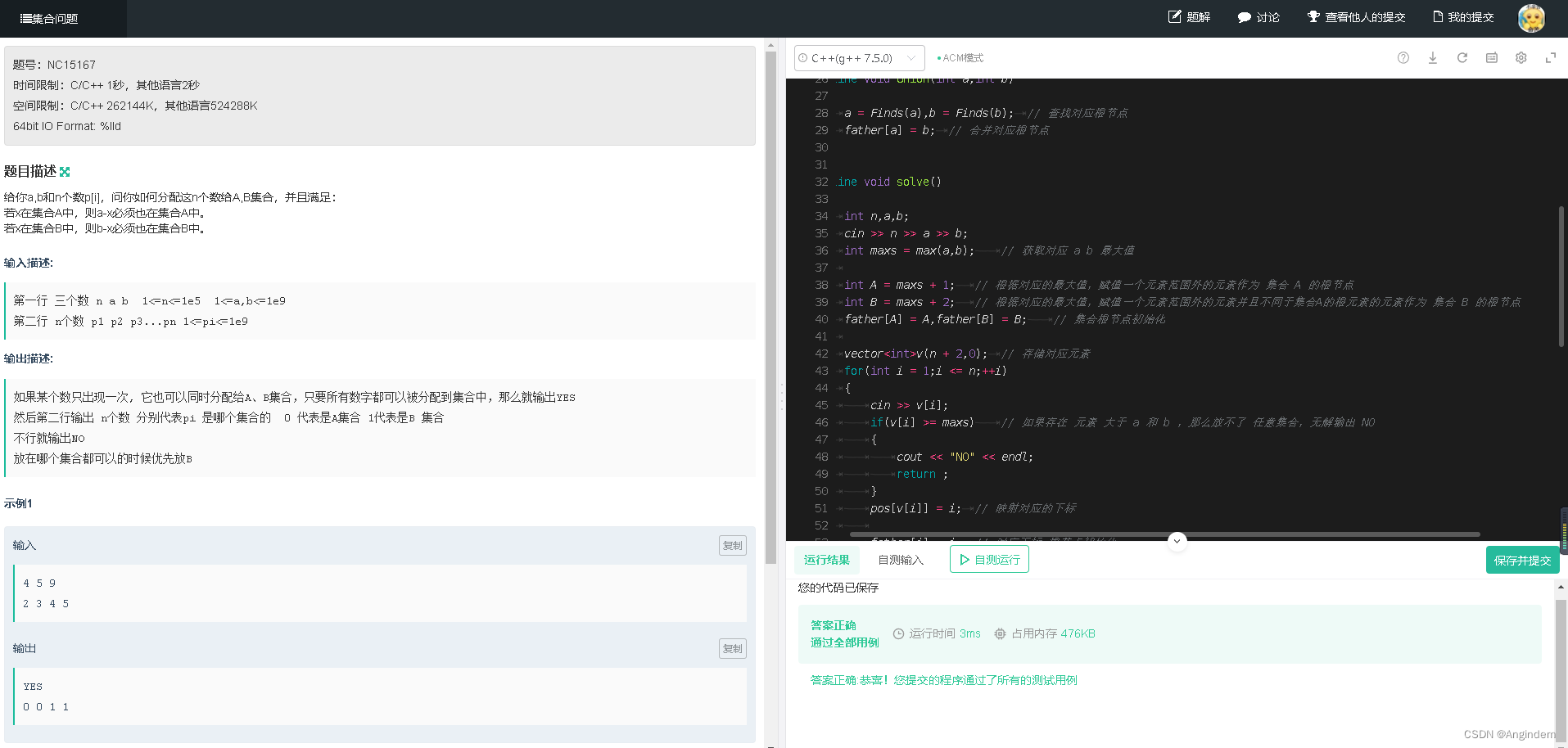
集合问题(并查集)
本题链接:登录—专业IT笔试面试备考平台_牛客网 题目: 样例1: 输入 4 5 9 2 3 4 5 输出 YES 0 0 1 1 样例2: 输入 3 3 4 1 2 4 输出 NO 思路: 这道题关键点在于。 当集合中有一个元素均存在于集合 A 和集合 B 的时…...

Ubuntu文件系统结构
Ubuntu文件系统结构 介绍 Ubuntu是一种备受欢迎的Linux发行版,其文件系统结构以及组织方式是每个使用者和系统管理员都应该了解的重要主题。本篇博客将带您深入探索Ubuntu文件系统的结构,以便更好地理解Linux操作系统的工作原理。 1. 根目录ÿ…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
