【深度学习理论】持续更新
文章目录
- 1.统计学习理论
1.统计学习理论
统计学习理论,一款适合零成本搞深度学习的大冤种的方向
从人类学习到机器学习的对比(学习的过程分为归纳和演绎 ),引出泛化和过拟合的概念。
如何表示归纳的函数规律呢?以监督问题为例,需要学习X到Y的映射,先做假设空间,为了使假设空间和真实映射接近,需要损失函数来优化假设空间。学习的目的是学习数据的分布而不是每一个数据点本身,所以希望期望风险最小(期望风险即假设在数据整个分布上的误差的期望),然而需要学习的分布是未知的,所以不能计算期望风险。但是假设在训练集上的误差是可以计算的(即经验风险,损失函数在训练集上的均值),所以下面的目标是追求经验风险最小化。

那么这个假设和假设空间里真正最优得到那个假设所达到的期望风险有多大差距呢?它和全函数类(包含所有可能得映射的函数类里所存在的能达到的最优的假设的风险,即Bayes error差多少),我们可以将经验风险和Bayes error的差距改写成经验风险和假设空间中的所能达到最优的risk的差距(即estimation error,假设空间中最优的risk和Bayes error之间的差距是approximation error),approximation error和具体的训练数据无关,只和假设空间的选择有关(假设空间固定,approximation error就是一个固定值,与训练数据和算法无关),所以只能找estimation error的上界。这里存在trade-off,如果选择更大的假设空间,那么approximation error就会相应地变小。如果假设空间大到包含了最优的Bayes classifier,那么approximation error就是0。但是随着假设空间的增大,训练的cost也会相应增加(亦有可能出现过拟合,estimation error变大,没有泛化能力,没有学到数据背后的规律)

学习数据背后的规律这件事靠谱吗?如何保证学到的数据验证集上靠谱呢?根据大数定律:在随机事件的大量重复中往往会呈现几乎必然的规律,当样本集无限大,样本均值趋近于总体均值。

摆脱对极限和无穷的依赖,人为设定一个界\epsilon,若经验风险和期望风险的差距小于\epsilon则可以接受。霍夫丁不等式帮助判断一个假设的优劣,优劣通过置信度\delta表现,对于一个假设\delta越小越好,\delta越小代表无法接受的结果出现的概率也就越小。霍夫丁不等式就像绑住期望风险和经验风险之间的弹力绳,在具体情况中期望风险和经验风险谁高谁低不好说,但是有了中间的弹力绳,我们用力拉低经验风险,期望风险大概率也可以被拉低,大部分情况下期望风险和经验风险的差距是小于\epsilon的,但是中间是弹力绳,运气不好时,差距可能大于\epsilon,运气不好时超过\epsilon多少也是未知的,这样的双重不确定性听起来不靠谱

构建靠谱的框架,期望风险和经验风险都和假设h有关(假设h取值不同,期望风险和经验风险都不同)。下面图像,蓝色曲线是期望风险,黑色曲线是经验风险,都是以h为变量的函数,蓝色曲线最低点期望误差最小是optimal solution h^*,黑色曲线最低点是经验风险最小化的solution,不光假设影响经验风险,训练集也影响。但是不同的训练集对期望风险不会有影响,因为期望风险本身就是在全样本集上误差的期望。
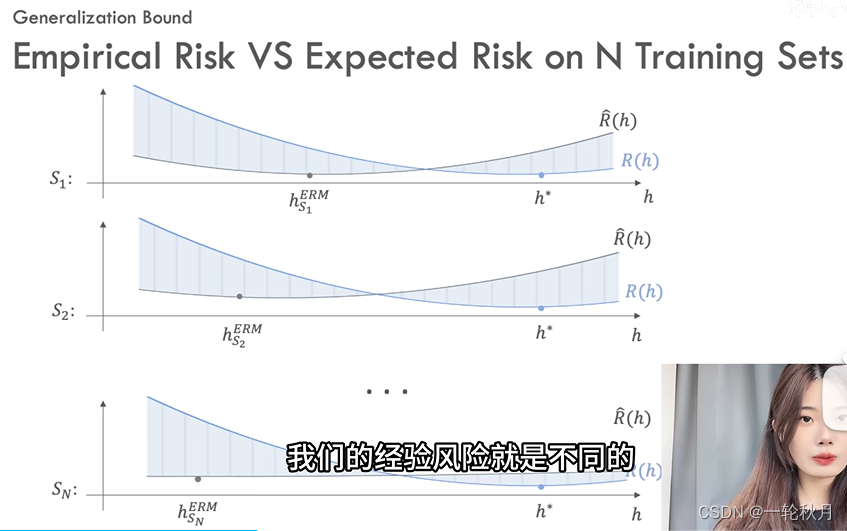
希望找到的假设期望风险也能越小越好,期望风险和经验风险的差值超过\epsilon为红色,小于为灰色,同样的假设在数据集1上小于\epsilon,但是在数据集2上又大于\epsilon
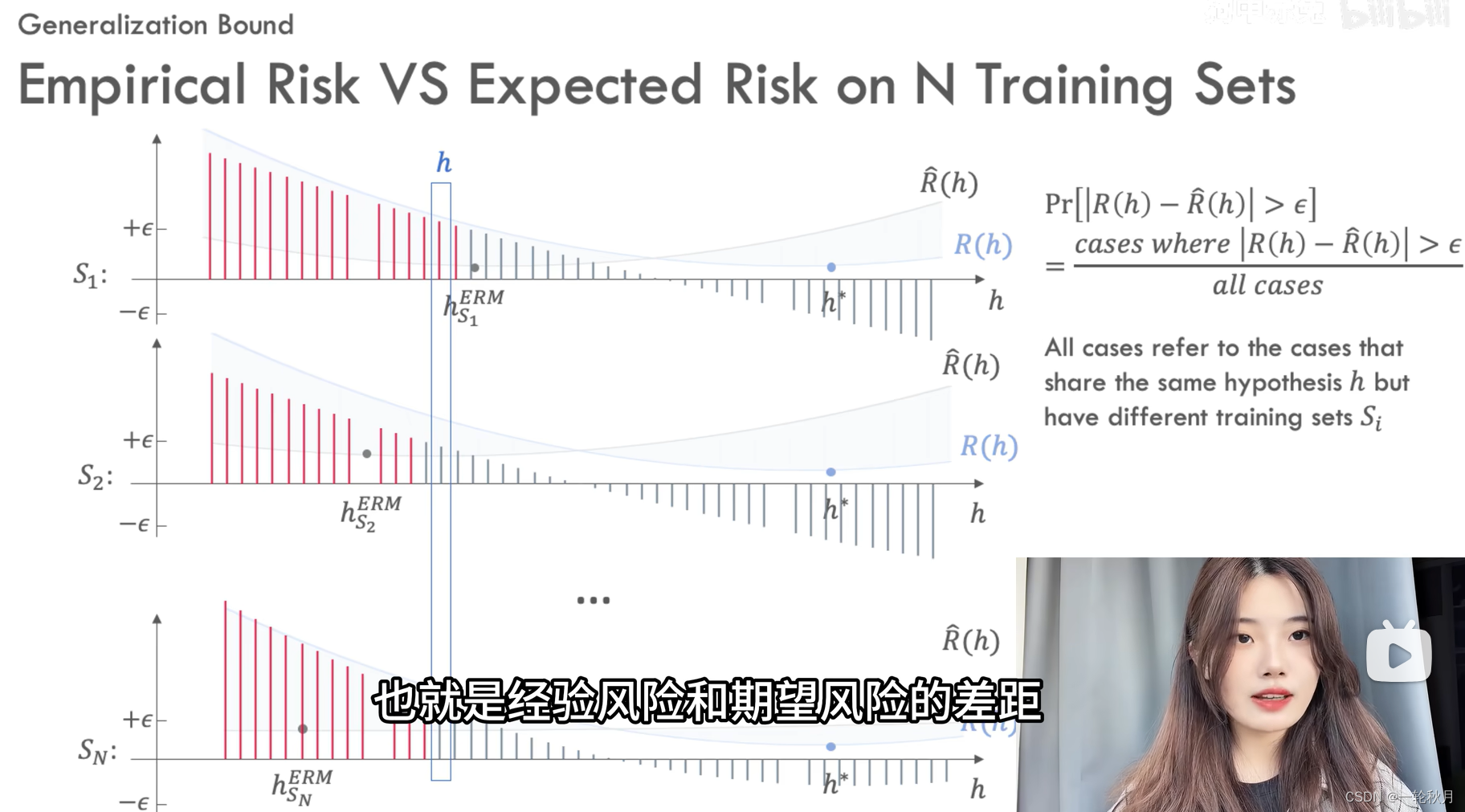
对于一个假设h,期望风险减去假设风险的绝对值大于\epsilon的概率,即在所有数据集上红色格子数量除以格子的总数,我们希望它可以小于一个上界\delta

定义PAC学习框架,提供了一套严格的形式化语言,来陈述和刻画可学习性
和样本复杂度的问题。我们希望在假设空间空间中找到期望风险为0的假设,但基本上不可能。所以退而求其次,只要期望风险小于等于\epsilon,则是可接受的,近似正确的(approximately correct)。我们也不是100%要求这个假设近似正确,它不需要对所有任意的数据都能成功预测,只要预测失败的概率小于非常小的数字\delta,我们就认为是可能正确的,也就是probably correct,我们把成功概率的下界1-\delta叫做置信度。满足上面两个条件,则我们的学习算法能够从假设空间h中辨识概念类c(即模型能够在合理的训练数据量中,通过合理的计算量,学到了一个很好的近似解)。不难发现,所需要的样本量和\epsilon \delta 算法复杂度 目标概念的复杂度都有关。算法也要考虑复杂度,如果算法运行复杂度也在这个多项式内,那么称概念类c是PAC可学习的。如果算法A是存在的,那么称此算法为这个概念类的一个PAC学习算法。如果算法处理每个样本的时间都是常数,那么算法的复杂度等价于样本的复杂度,如果时间复杂度过大,即使理论上行得通,我们也是跑不出一个结果的。

目标概念有两种可能得情况,1.我们想找的目标概念c在我们的假设空间;2.不在假设空间。目标概念c属于假设集h称为一致情况,反之称为不一致情况。考虑第一种情况:目标概念c在我们的假设空间,则排除所有在训练集s上除了错的假设了,但是假设空间里可能存在不止一个在训练集上不犯错的假设,这样我们没法通过训练集来判断这些假设哪个是最优的。那么我们先假设,假设h虽然在训练集上没有犯错,但是他的期望风险大于\epsilon。那么对于从分布D上采样得到的任意一个样本,我们的假设没犯错的概率小于1-\epsilon。那么h和包含m个服从D的训练集s一致的概率是小于(1-\epsilon)^m的。因为我们没有办法区分等效的假设,所以我们也不知道我们的学习算法选择了哪个假设,所以我们需要一个uniform convergence bound,也就是对所有一致的假设都成立的bound。根据联合界定理,事件和的概率小于等于事件概率的和,条件概率的定义是已知事件A发生的情况下,事件B发生的概率等于AB同时发生的概率和事件A发生的概率的比,事件A发生的概率一定小于等于1。所以A发生的情况下,事件B发生的条件概率大于等于AB同时发生的概率。回忆刚才推过的假设在训练集s上不犯错,但是期望风险大于\epsilon的概率是小于(1-\epsilon)^m的。我们需要所有的泛化误差大于\epsilon的一致假设出现的概率之和不大于\delta,这样我们容易得到样本复杂度

不难看出当假设空间有限,算法A是一个PAC学习算法,样本复杂度是一个关于1/\epsilon和1/\delta的多项式。同时期望风险的上界是随着样本规模m的增长而下降的,泛化误差减小的速率是O(1/m),我们平时也会发现使用大规模的有标签的数据集会让训练效果更好,同时期望风险的上界也随着假设集的势的增长而增长(即我们的假设集越大我们越难学到我们想要的东西,只不过他的增长速率是log级别的)

证明一致情形的例子,考虑概念类C_n是最多n个boolean变量的合取x_1,x_2 x_n,当n=4,想学习的概念类是x_1与非x_2与x_4,1001是正样本,1000是负样本。我们不知道目标概念,只知道n=4,1001是个正样本,我们通过分析样本得到一些信息:既然1001是正样本,则说明目标概念不包括非x_1和非x_3,也不包括x_2和x_4,但是负样本就不能传递这么多的信息,因为我们不知道x_1 x_2 x_3 x_4哪个是错的

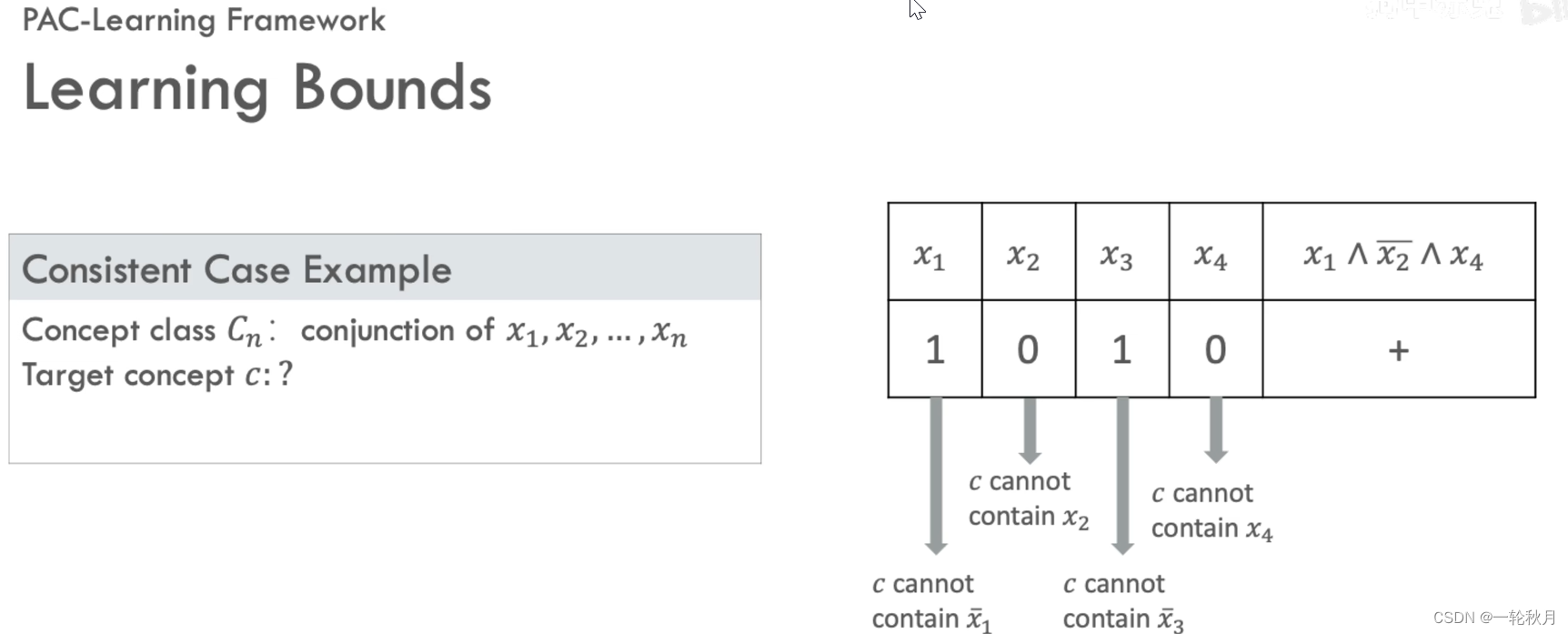
n=6的情况,我们想找到一个算法,来根据正样本找到一个一致的假设,那么对于每一个正样本,如果它的哪一位是1,那么目标概念就应该排除它的否定式,如果它的哪一位是0,我们就可以排除它本身,按此方法推出目标概念是非x_1 与x_2 与x_5与 x_6。这个问题我们是知道假设空间的大小的
相关文章:

【深度学习理论】持续更新
文章目录 1.统计学习理论 1.统计学习理论 统计学习理论,一款适合零成本搞深度学习的大冤种的方向 从人类学习到机器学习的对比(学习的过程分为归纳和演绎 ),引出泛化和过拟合的概念。 如何表示归纳的函数规律呢?以监督…...

npm ERR! reason: certificate has expired(淘宝镜像过期)
npm ERR! request to https://registry.npm.taobao.org/yauzl/-/yauzl-2.4.1.tgz failed, reason: certificate has expired 今天在执行npm install命令时,报错百度了下是淘宝证书过期原因 解决方法一 执行下面两个命令再进行npm install即可 npm cache clean --…...

“极简壁纸“爬虫JS逆向·实战
文章目录 声明目标分析确定目标目标检索 代码补全完整代码 爬虫逻辑完整代码 运行结果 声明 本教程只用于交流学习,不可用于商业用途,不可对目标网站进行破坏性请求,请遵守相关法律法规。 目标分析 确定目标 获取图片下载链接 目标检索…...
Django通过Json配置文件分配多个定时任务
def load_config():with open("rule.json", rb)as f:config json.load(f)return configdef job(task_name, config, time_interval):# ... 通过task_name判断进行操作if task_name get_data_times:passdef main():config load_config()for task_name, task_value…...
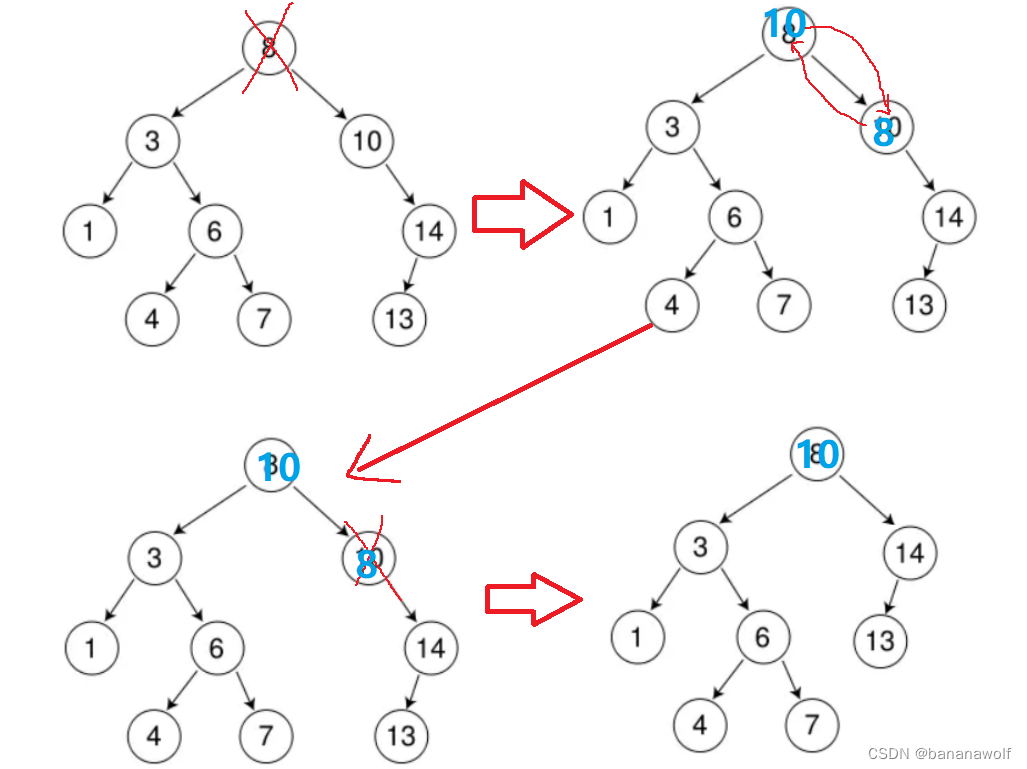
C++ 搜索二叉树的删除
首先查找元素是否在二叉搜索树中,如果不存在,则返回 要删除的结点可能分下面四种情况: a. 要删除的结点无孩子结点 b. 要删除的结点只有左孩子结点 c. 要删除的结点只有右孩子结点 d. 要删除的结点有左、右孩子结点 看起来有待删除节点有4中…...
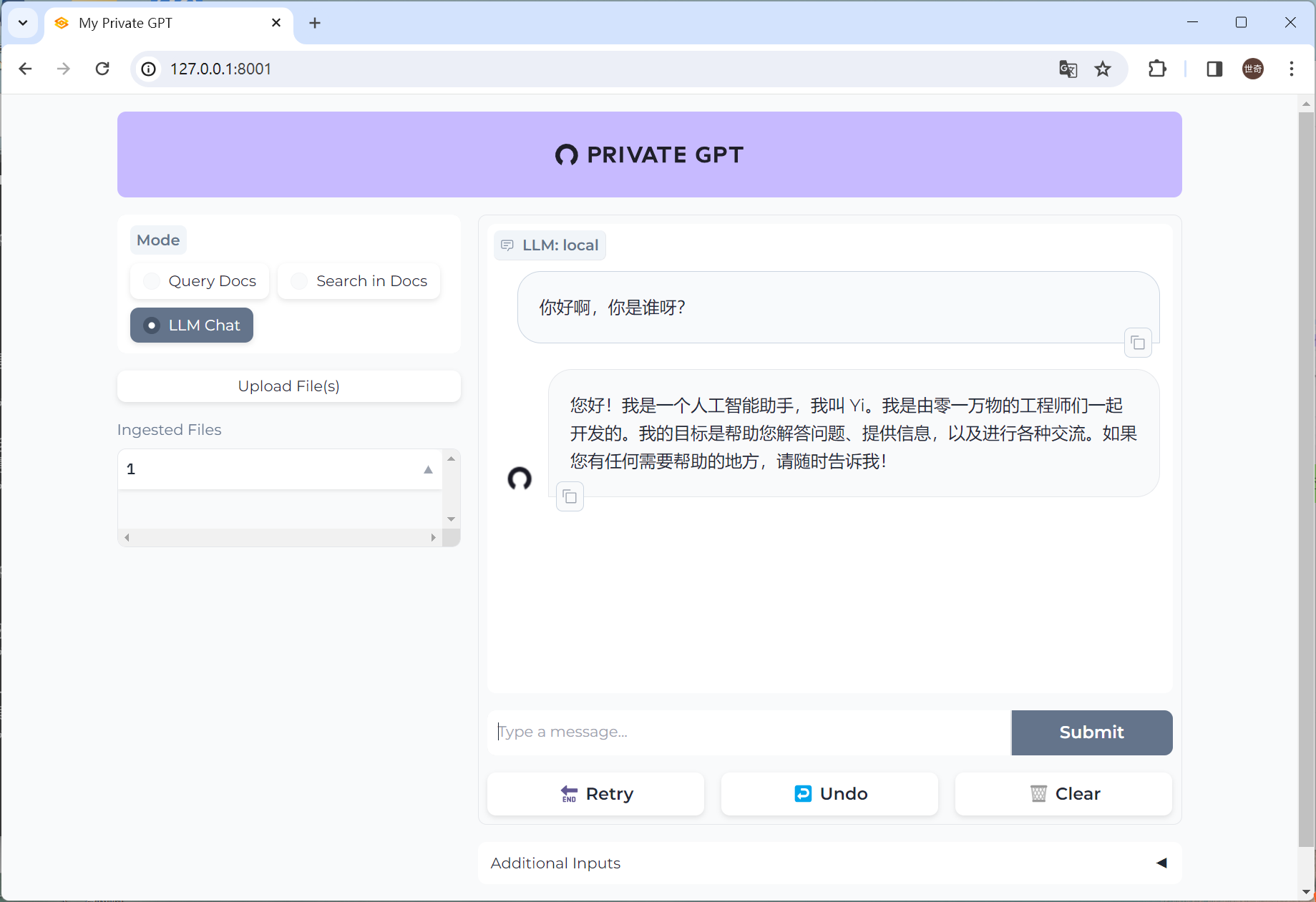
构建中国人自己的私人GPT—支持中文
上一篇已经讲解了如何构建自己的私人GPT,这一篇主要讲如何让GPT支持中文。 privateGPT 本地部署目前只支持基于llama.cpp 的 gguf格式模型,GGUF 是 llama.cpp 团队于 2023 年 8 月 21 日推出的一种新格式。它是 GGML 的替代品,llama.cpp 不再…...

elementui 回到顶部报错
<template>Scroll down to see the bottom-right button.<el-backtop target".page-component__scroll .el-scrollbar__wrap"></el-backtop> </template> 使用element的Backtop 回到顶部组件的伙伴们,把官网代码复制到页面使用时…...

go-carbon v2.3.8 发布,轻量级、语义化、对开发者友好的 golang 时间处理库
carbon 是一个轻量级、语义化、对开发者友好的 golang 时间处理库,支持链式调用。 目前已被 awesome-go 收录,如果您觉得不错,请给个 star 吧 github.com/golang-module/carbon gitee.com/golang-module/carbon 安装使用 Golang 版本大于…...
【详解】斗地主随机发牌项目
目录 前言: 1.初始化牌 2.洗牌 3.揭牌 总代码: Card类: CardGame类: Main类: 结语: 前言: 斗地主是全国范围内的一种桌面游戏,本节我们来实现一下斗地主中的简单初始化牌、…...

多账号运营为什么要使用动态住宅代理IP?
对于跨境有多账号运营需求的企业来说,选择正确类型的代理IP对于平稳运行至关重要。但最适合这项工作的代理类型是什么?为了更好地管理不同平台上的多个账户并优化成本,您可以选择动态住宅代理。 一、什么是动态住宅代理 动态住宅代理IP是互联…...
[C++] 如何使用Visual Studio 2022 + QT6创建桌面应用
安装Visual Studio 2022和C环境 [Visual Studio] 基础教程 - Window10下如何安装VS 2022社区版_visual studio 2022 社区版-CSDN博客 安装QT6开源版 下载开源版本QT Try Qt | 开发应用程序和嵌入式系统 | Qt Open Source Development | Open Source License | Qt 下载完成&…...

Arduino 推出基于乐鑫 ESP32-S3 的 STEM 教育机器人
Arduino Alvik 是 Arduino Education 推出的一款新型机器人,可作为一种跨学科工具,为当前教育和未来机器人世界筑起连接的桥梁。Hackster 的 Gareth Halfacree 表示:“Alvik 的设计灵感来自 Arduino 简化复杂技术的理念,同时它也 …...

Blender使用Rigify和Game Rig Tool基础
做动画需要的几个简要步骤: 1.建模 2.绑定骨骼 3.绘制权重 4.动画 1.Rigify是干嘛用的? 》 绑定骨骼 2.Game Rig Tool干嘛用的? 》 修复Rigify绑定骨骼做的动画导入游戏引擎的问题,如果Rigify自身修复了就不需要这个插件了&#…...
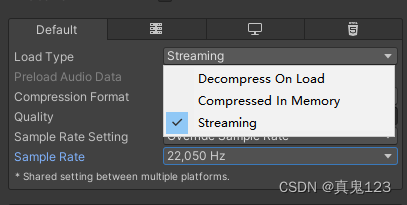
【Unity优化(一)】音频优化
整理资教程:https://learn.u3d.cn/tutorial/unity-optimization-metaverse 1.音频优化 音频一般不会成为性能瓶颈,是为了节省内存和优化包体大小。 1.0 文件格式和压缩格式 原始音频资源尽量采用WAV格式。 移动平台音频尽量采用Vorbis压缩格式&#x…...

算法.1-三大排序算法-对数器-二分
三大排序算法&对数器 1.选择排序 Java版 package class01;import java.util.Arrays;public class Code01_SelectionSort {public static void selectionSort(int[] arr) {if (arr null || arr.length < 2) {return;}// 0 ~ N-1 找到最小值,在哪…...
详解)
Midjourney新功能介绍:风格参考(Style References)详解
引言 对于追求创意和一致性的艺术家和设计师们来说,Midjourney的最新功能——风格参考(Style References),无疑是一个激动人心的消息。这项测试算法的发布,让我们得以通过简单的URL引用,将特定的风格应用于…...

C++ 11/14/17 智能指针
1. 简介 为了更加容易(更加安全)的使用动态内存,引入了智能指针的概念。智能指针的行为类似常规指针,重要的区别是它负责自动释放所指向的对象。 标准库提供的两种智能指针的区别在于管理底层指针的方法不同:shared_p…...

C++入门【37-C++ 拷贝构造函数】
拷贝构造函数是一种特殊的构造函数,它在创建对象时,是使用同一类中之前创建的对象来初始化新创建的对象。拷贝构造函数通常用于: 通过使用另一个同类型的对象来初始化新创建的对象。复制对象把它作为参数传递给函数。复制对象,并…...
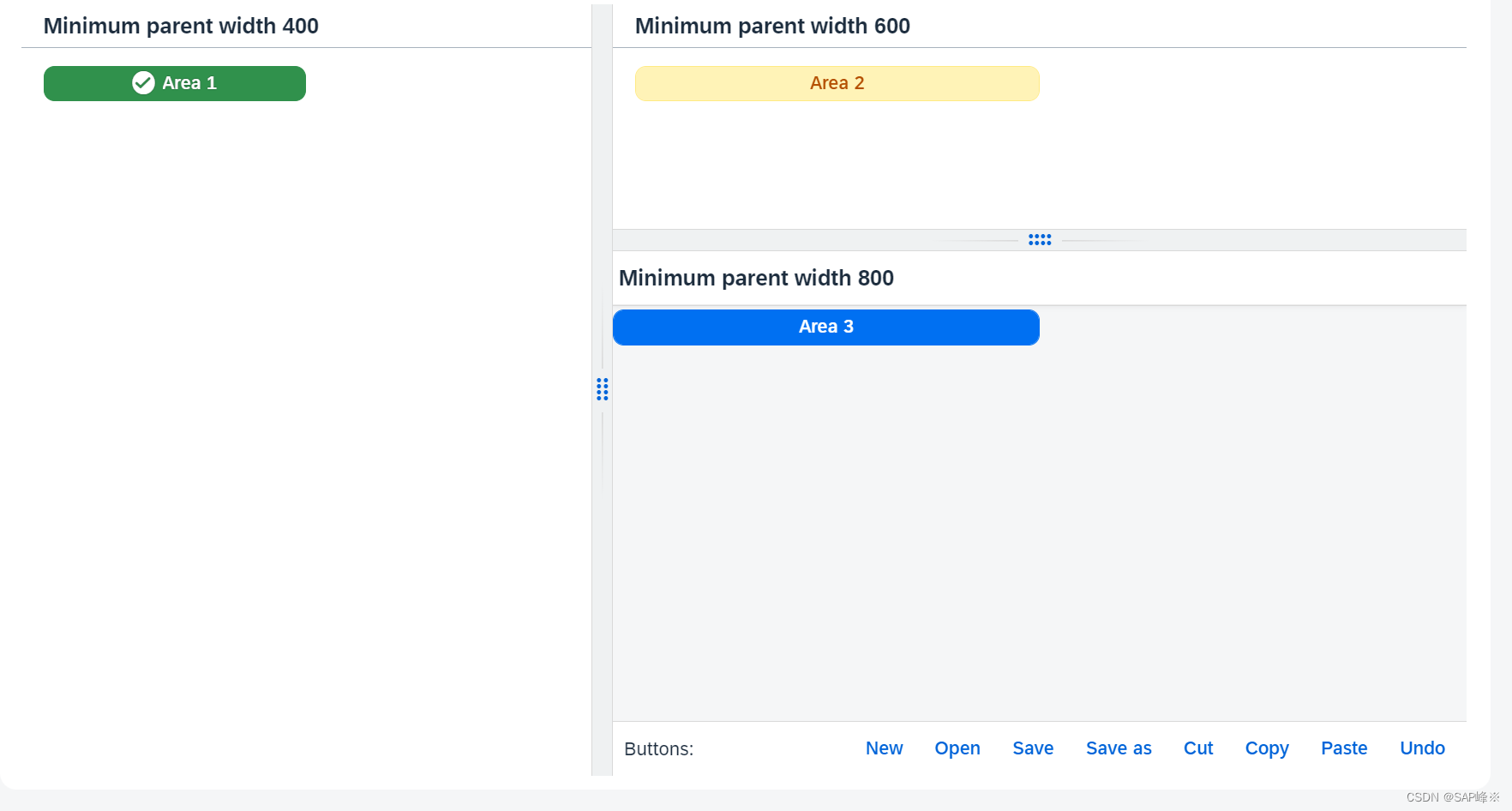
[UI5 常用控件] 06.Splitter,ResponsiveSplitter
文章目录 前言1. Splitter1.1 属性 2. ResponsiveSplitter 前言 本章节记录常用控件Splitter,ResponsiveSplitter。主要功能是分割画面布局。 其路径分别是: sap.ui.layout.Splittersap.ui.layout.ResponsiveSplitter 1. Splitter 1.1 属性 orientation &#x…...

C遗漏知识(个人向)
之前C语言遗漏的一些。 数据在内存中的存储 原码、反码、补码 整数的2进制表⽰⽅法有三种,即 原码、反码和补码 正整数的原、反、补码都相同。 负整数的三种表⽰⽅法各不相同。 原码:直接将数值按照正负数的形式翻译成⼆进制得到的就是原码。 反码&…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...
