C++ dfs搜索枚举(四十八)【第八篇】
曾经我们讲过枚举算法,那假设我们把枚举算法应用到搜索里呢?
1.搜索枚举
以前我们在进行枚举的时候是用了多层循环嵌套,但是当枚举的变量过多或者是输入的数量的时候就很难利用循环完成枚举了,不过我们可以尝试利用搜索进行枚举。
通常,我们通过一个 dfs 函数来完成搜索枚举,而通过参数表示当前状态。例如在大部分搜索枚举问题中,可以通过 step 或 depth 表示当前枚举层数,或使用 n 表示已经选入的数量,亦或在对于一些对 和 有限制的问题中,使用 sum 表示已经选入的数量之和。
让我们看一道能够使用搜索枚举实现的题目:现有方程a[1]x[1]+a[2]x[2]+a[3]x[3]+...+a[n]x[n]=0 2≤n≤10,−5≤a[i]≤5,−2≤x[i]≤2,x[i]∈Z
求解的总数。
Z 表示整数集合,其包括了:全体正整数、全体负整数和零。
能够估算所有的状态总数在 10的5次方∼10的7次方,能够枚举全部的状态。虽然能够使用 10 个循环完成,但此处使用搜索枚举更为方便。
int ans = 0;
void dfs(int dep, int sum) {if (dep == n) {if (sum == 0){ans++;}return;}for (int i = -2; i <= 2; i++) {dfs(dep + 1, sum + a[dep] * i);}
}在很多搜索枚举的问题中,会要求我们打印解的具体内容,那么可使用数组来保存具体的解。如对于之前求方程解的问题,可将代码修改为:
int ans[15];
void dfs(int dep, int sum) {if (dep == n) {if (sum == 0){for (int i = 0; i < n; i++) {cout << ans[i] << " ";}cout << endl;}return ;}for (int i = -2; i <= 2; i++) {ans[dep] = i;dfs(dep + 1, sum + a[dep] * i);}
}把在dep这一层选择的情况放在ans[dep]位置,ans数组就记下了目前枚举到的情况。n
在搜索枚举的过程中,我们能够根据题目的一些性质,对求解的过程进行剪枝优化,这个我们以后也会学到。但是对大部分题目来说,搜索枚举很有可能达到状态的上限,所以很有必要在决定使用搜索枚举之前确定状态的总数。
相关文章:
【第八篇】)
C++ dfs搜索枚举(四十八)【第八篇】
曾经我们讲过枚举算法,那假设我们把枚举算法应用到搜索里呢? 1.搜索枚举 以前我们在进行枚举的时候是用了多层循环嵌套,但是当枚举的变量过多或者是输入的数量的时候就很难利用循环完成枚举了,不过我们可以尝试利用搜索进行枚举。…...

【优先级队列(大顶堆 小顶堆)】【遍历哈希表键值对】Leetcode 347 前K个高频元素
【优先级队列(大顶堆 小顶堆)】【排序】Leetcode 347 前K个高频元素 1.不同排序法归纳2.大顶堆和小顶堆3.PriorityQueue操作4.PriorityQueue的升序(默认)与降序5.问题解决:找前K个最大的元素 :踢走最小的&…...

Java设计模式-模板方法模式(14)
行为型模式 行为型模式用于描述程序在运行时复杂的流程控制,即描述多个类或对象之间怎样相互协作共同完成单个对象都无法单独完成的任务,它涉及算法与对象间职责的分配。行为型模式分为类行为模式和对象行为模式,前者采用继承机制来在类间分派行为,后者采用组合或聚合在对…...

【C++ 二维前缀和】约会
题目描述 从前,小兔发现了一个神秘的花园。 花园是一个 n 行 m 列的矩阵,第 i 行 j 列的花的美丽度为 ai,j,一个合法的约会场所为任意一个正方形子矩阵,定义子矩阵的浪漫度为这个子矩阵的两条对角线上的花的美丽度之和。 现在小兔…...
基于Springboot的社区疫情防控平台
末尾获取源码作者介绍:大家好,我是墨韵,本人4年开发经验,专注定制项目开发 更多项目:CSDN主页YAML墨韵 学如逆水行舟,不进则退。学习如赶路,不能慢一步。 一、项目简介 以往的社区疫情防控管理…...

JAVA中的类方法
一、定义 1.类方法也叫静态方法 格式 访问修饰符 static 数据返回类型 方法名(){} 2.类方法的调用 前提:满足访问修饰符的访问权限 使用方式:类名.类方法名或者对象名.类方法名 二、注意事项 1.类方法中没有this的参数 class D{private int n1 …...

rust嵌入式开发之RTICvsEmbassy
RTIC和Embassy是目前rust嵌入式开发中比较热门的两个框架。本来呢,针对RTIC的移植已经完成了一小半,但在移植过程中感受到了RTIC的不足,正好跳出来全面考察下embassy,本文就是根据目前的尝试结果做个对比总结。 RTIC和Embassy是两…...

Bug地狱 #1 突然宕机,企业级应用到底怎么了
Bug地狱 #1 突然宕机,企业级应用到底怎么了 背景 目前就职的企业经营是一家服务小微门店Saas企业,以进销存管理和客户营销为主体提供订阅服务。项目正式上线可以说是从13年,基础架构是Web和后端使用C# .net,数据库使用SQL Serve…...
使用 Python、Elasticsearch 和 Kibana 分析波士顿凯尔特人队
作者:来自 Jessica Garson 大约一年前,我经历了一段压力很大的时期,最后参加了一场篮球比赛。 在整个过程中,我可以以一种我以前无法做到的方式断开连接并找到焦点。 我加入的第一支球队是波士顿凯尔特人队。 波士顿凯尔特人队是…...
探索C语言结构体:编程中的利器与艺术
✨✨ 欢迎大家来到贝蒂大讲堂✨✨ 🎈🎈养成好习惯,先赞后看哦~🎈🎈 所属专栏:C语言学习 贝蒂的主页:Betty‘s blog 1. 常量与变量 1. 什么是结构体 在C语言中本身就自带了一些数据类型&#x…...
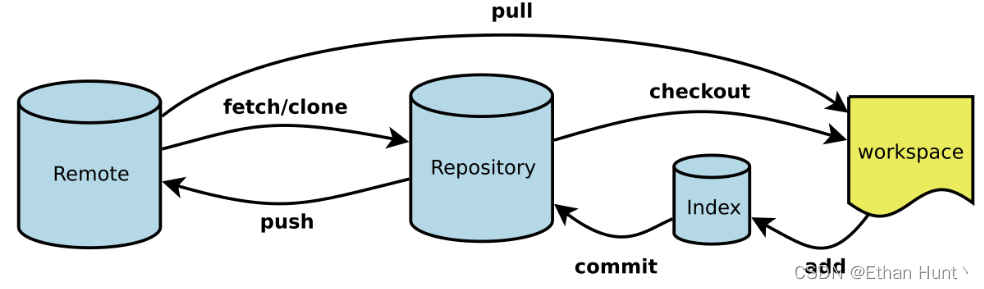
Git介绍与常用命令总结
Git介绍与其常用命令总结 1、Git介绍2、Git的使用3、Git常用命令3.1 初始化仓库3.2 克隆仓库3.3 配置用户信息3.4 提交代码(Commit)3.5 推送代码(Push)3.6 拉取代码(Pull)3.7 分支(Branch)3.8 远程仓库(Remote)3.9 撤销回退本地改动3.10 更新本地仓库与远程仓库 1、Git介绍 Gi…...
机器学习 | 探索朴素贝叶斯算法的应用
朴素贝叶斯算法是一种基于贝叶斯定理和特征条件独立假设的分类算法。它被广泛应用于文本分类、垃圾邮件过滤、情感分析等领域,并且在实际应用中表现出色。 朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法: 1)对于给定的待分类项r…...
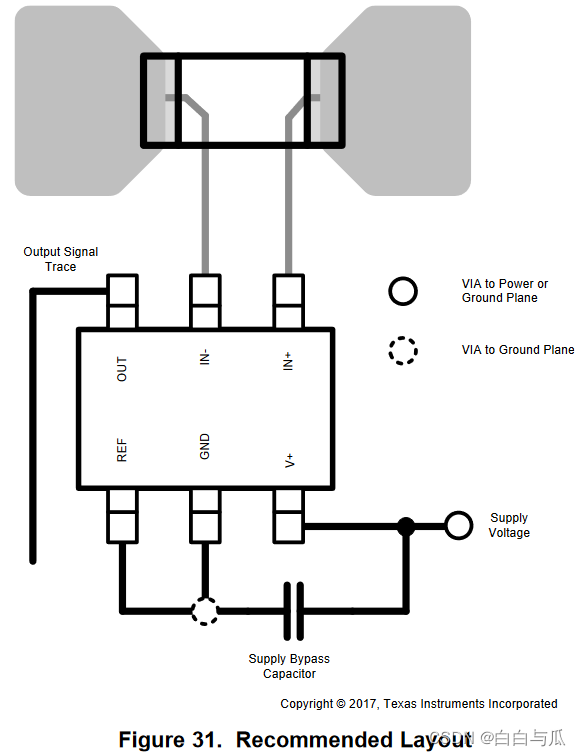
【无刷电机学习】电流采样电路硬件方案
【仅作自学记录,不出于任何商业目的】 目录 AD8210 INA282 INA240 INA199 AD8210 【AD8210数据手册】 在典型应用中,AD8210放大由负载电流通过分流电阻产生的小差分输入电压。AD8210抑制高共模电压(高达65V),并提供接地参考缓冲输出&…...

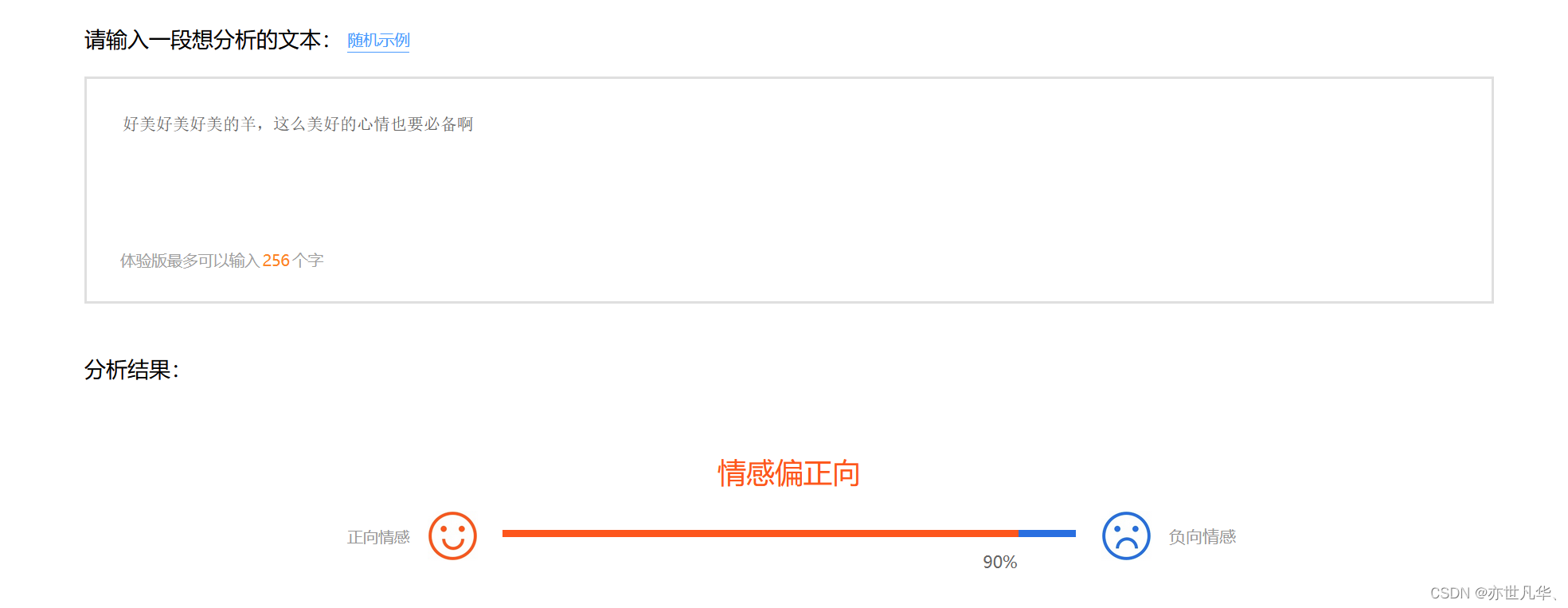
对于协同过滤算法我自己的一些总结和看法
文章目录 协同过滤算法的基本原理协同过滤算法的分类用户相似度计算UserCF && ItemCF应用场景 协同过滤算法的优缺点优点缺点 协同过滤算法的总结与展望Q&A 协同过滤算法的基本原理 关于协同过滤算法,我看过很多老师写的博客以及一些简单的教程&#x…...
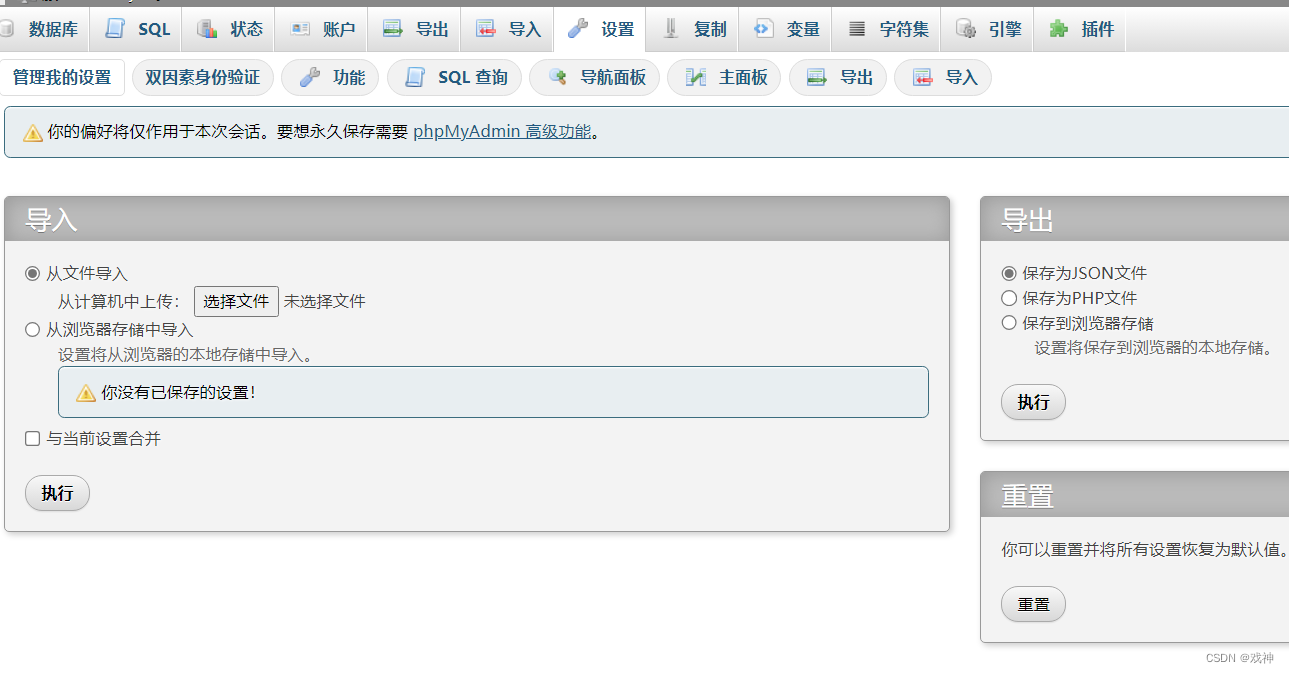
数据库管理phpmyadmin
子任务1-PHPmyadmin软件的使用 本子任务讲解phpmyadmin的介绍和使用操作。 训练目标 1、掌握PHPmyadmin软件的使用方法。 步骤1 phpMyAdmin 介绍 phpmyadmin是一个用PHP编写的软件工具,可以通过web方式控制和操作MySQL数据库。通过phpMyAdmin可以完全对数据库进行…...
Oracle数据表ID自增操作
一、Oracle ID自增长功能介绍 Oracle数据库默认不支持像 SQLServer、MySQL中的自增长(auto increment)功能,即自动为每一行记录的自增长字段生成下一个值。 二、Oracle ID自增长方法 第一种,通过序列(sequence&#…...

npm WARN deprecated uuid@3.4.0: Please upgrade to version 7 or higher
当使用npm下载vue3-lazy时出现一下错误时的解决方案 报错:npm WARN deprecated uuid3.4.0: Please upgrade to version 7 or higher 尝试使用过一下命令更新 npm install uuidlatest -g 是安装了最新版本的uuid, 再次下载已解决问题 ***但看某些播客依…...

第2节、让电机转起来【51单片机+L298N步进电机系列教程】
↑↑↑点击上方【目录】,查看本系列全部文章 摘要:本节介绍用简单的方式,让步进电机转起来。其目的之一是对电机转动有直观的感受,二是熟悉整个开发流程。本系列教程必要的51单片机基础包括IO口操作、中断、定时器三个部分&#…...

1154: 第多少天
题目描述 定义一个包括年、月、日的结构体变量,读入年、月、日,计算该日在当年中是第几天。注意闰年问题。 输入描述 三个整数,分别表示年、月、日。保证输入是实际存在的日期,且年份在1000至3000之间(包含1000和30…...
【C语言初阶-const作用详解】const修饰变量、const修饰指针(图文详解版)
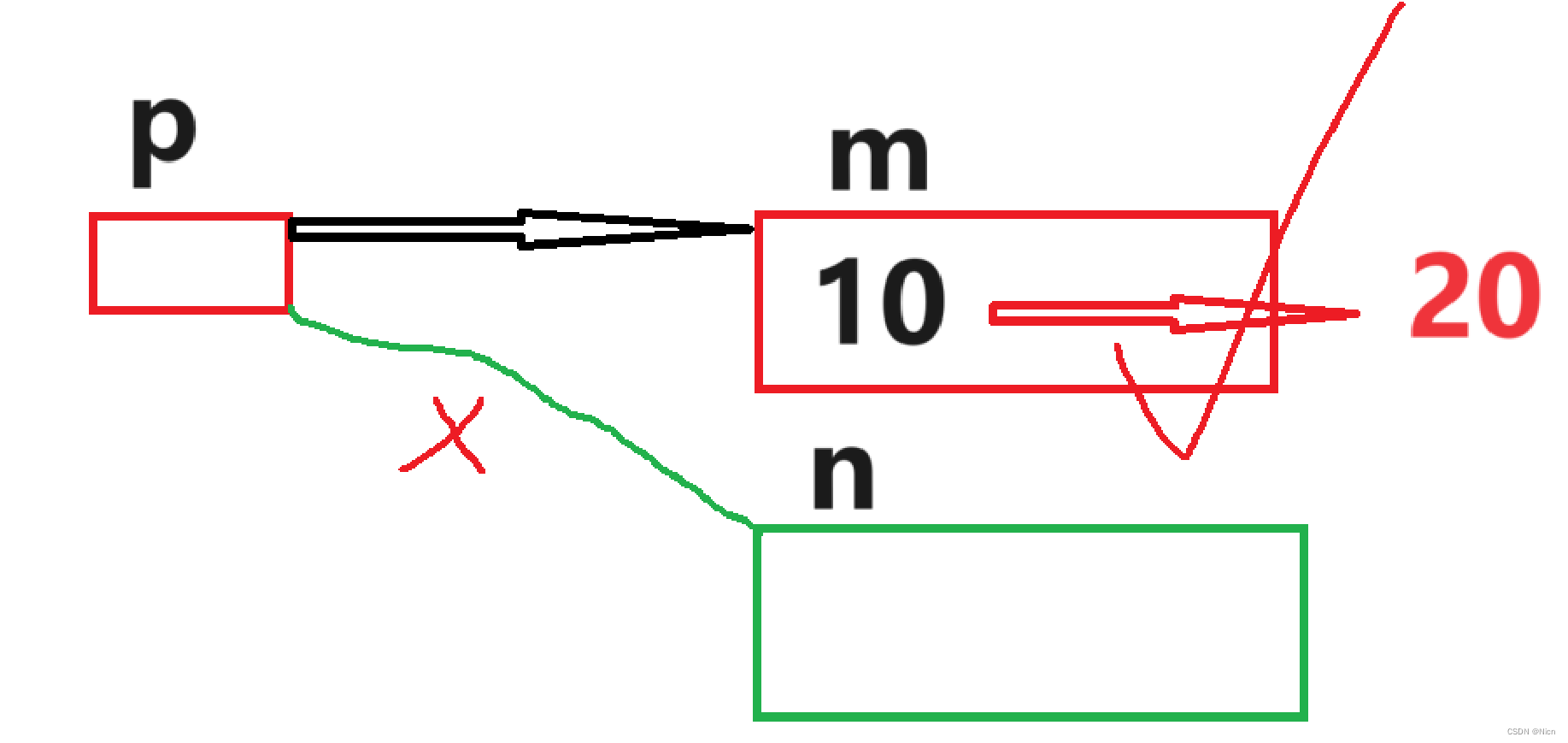
少年,做你认为对的事 目录 少年,做你认为对的事 1.const修饰变量 2.const修饰指针(重要) 代码1: 代码2: 代码3: 编辑 3.结论 1.const修饰变量 const修饰变量将变量赋予了常量属性…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

表单设计器拖拽对象时添加属性
背景:因为项目需要。自写设计器。遇到的坑在此记录 使用的拖拽组件时vuedraggable。下面放上局部示例截图。 坑1。draggable标签在拖拽时可以获取到被拖拽的对象属性定义 要使用 :clone, 而不是clone。我想应该是因为draggable标签比较特。另外在使用**:clone时要将…...

「Java基本语法」变量的使用
变量定义 变量是程序中存储数据的容器,用于保存可变的数据值。在Java中,变量必须先声明后使用,声明时需指定变量的数据类型和变量名。 语法 数据类型 变量名 [ 初始值]; 示例:声明与初始化 public class VariableDemo {publi…...

基于Java项目的Karate API测试
Karate 实现了可以只编写Feature 文件进行测试,但是对于熟悉Java语言的开发或是测试人员,可以通过编程方式集成 Karate 丰富的自动化和数据断言功能。 本篇快速介绍在Java Maven项目中编写和运行测试的示例。 创建Maven项目 最简单的创建项目的方式就是创建一个目录,里面…...
