LeetCode、62.不同路径的数目(一)【简单,动态规划或递归】
文章目录
- 前言
- LeetCode、62.不同路径的数目(一)【简单,动态规划或递归】
- 题目描述与分类
- 思路
- 思路1:动态规划
- 思路2:递归实现
- 简洁写法补充:2024.1.30
- 资料获取
前言
博主介绍:✌目前全网粉丝2W+,csdn博客专家、Java领域优质创作者,博客之星、阿里云平台优质作者、专注于Java后端技术领域。
涵盖技术内容:Java后端、算法、分布式微服务、中间件、前端、运维、ROS等。
博主所有博客文件目录索引:博客目录索引(持续更新)
视频平台:b站-Coder长路
LeetCode、62.不同路径的数目(一)【简单,动态规划或递归】
题目描述与分类
牛客:不同路径的数目(一)
leetcode:LeetCode、62.不同路径的数目(一)【简单,动态规划或递归】
题目内容:一个机器人在m×n大小的地图的左上角(起点)。机器人每次可以向下或向右移动。机器人要到达地图的右下角(终点)。
可以有多少种不同的路径从起点走到终点?
思考区
分类:动态规划/线性DP(二维)
约束条件:
1、机器人每次只能往右或者往下走。
2、机器人不能越界。
思路
思路1:动态规划
定义状态方程:
dp[i][j] = val i表示行,j表示列,val表示方案数量
当i>1 && j>1 dp[i][j] = dp[i][j-1] + dp[i-1][j]
当i=0时,dp[i][j] = dp[i][j-1]
当j=0时,dp[i][j] = dp[i-1][j]
复杂度分析:
- 时间复杂度:O(n*m)
- 空间复杂度:O(n*m)
代码:
import java.util.*;public class Solution {/*** * @param m int整型 * @param n int整型 * @return int整型*/public int uniquePaths (int m, int n) {//定义dp数组int[][] dp= new int[m][n];for (int i = 0;i < m; i++) {for (int j = 0; j < n; j++) {if (i == 0) {dp[i][j] = 1;continue;}if (j == 0) {dp[i][j] = 1;continue;}dp[i][j] = dp[i-1][j] + dp[i][j-1];}}return dp[m-1][n-1];}
}class Solution {//线性dp//dp(i, j) = dp(i-1,j) + dp(i,j-1)public int uniquePaths(int m, int n) {int[][] dp = new int[m][n];for (int i = 0; i < m; i ++) {for (int j = 0; j < n; j ++) {if (i == 0 || j == 0) dp[i][j] = 1;else dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
}
思路2:递归实现
import java.util.*;public class Solution {/*** * @param m int整型 * @param n int整型 * @return int整型*/public int uniquePaths (int m, int n) {if (m == 1 || n == 1) {return 1; }return uniquePaths(m - 1, n) + uniquePaths(m, n - 1);}
}
上面的时间复杂度是2n,如何优化呢?进行记忆化状态方程
class Solution {private int[][] dp;public int uniquePaths(int m, int n) {if (dp == null) {dp = new int[m + 1][n + 1];}if (m == 1 || n == 1) {return 1;}if (dp[m][n] == 0) {dp[m][n] = uniquePaths(m - 1, n) + uniquePaths(m, n - 1);}return dp[m][n];}
}
简洁写法补充:2024.1.30
class Solution {int[][] dp = new int[101][101];//线性dp//dp(i, j) = dp(i-1,j) + dp(i,j-1)public int uniquePaths(int m, int n) {if (m == 1 || n == 1) dp[m][n] = 1;if (dp[m][n] != 0) return dp[m][n];dp[m][n] = uniquePaths(m - 1, n) + uniquePaths(m, n - 1);return dp[m][n];}
}
此时无论是时间还是空间复杂度与思路1一致。
资料获取
大家点赞、收藏、关注、评论啦~
精彩专栏推荐订阅:在下方专栏👇🏻
- 长路-文章目录汇总(算法、后端Java、前端、运维技术导航):博主所有博客导航索引汇总
- 开源项目Studio-Vue—校园工作室管理系统(含前后台,SpringBoot+Vue):博主个人独立项目,包含详细部署上线视频,已开源
- 学习与生活-专栏:可以了解博主的学习历程
- 算法专栏:算法收录
更多博客与资料可查看👇🏻获取联系方式👇🏻,🍅文末获取开发资源及更多资源博客获取🍅
整理者:长路 整理时间:2024.1.31
相关文章:
【简单,动态规划或递归】)
LeetCode、62.不同路径的数目(一)【简单,动态规划或递归】
文章目录 前言LeetCode、62.不同路径的数目(一)【简单,动态规划或递归】题目描述与分类思路思路1:动态规划思路2:递归实现简洁写法补充:2024.1.30 资料获取 前言 博主介绍:✌目前全网粉丝2W,csdn博客专家、…...

re:从0开始的CSS学习之路 4. 长度单位
1. 长度单位 像素px:一个像素就是屏幕中一个不可分割的点。我们应用的屏幕实际上是由一个个的像素点构成的。 不同显示器的像素点大小也不同,在屏幕尺寸相同的情况下,像素越小,显示效果越清晰。 大部分浏览器默认字体大小是16px …...

golang开源定时任务调度框架
golang开源定时任务调度框架 Go语言中有很多开源的定时任务调度框架,以下几个是比较流行常用的: golang开源定时任务框架介绍 cron 一个基于Cron表达式的定时任务库,可以精确到秒级。它提供了简单易用的API来定义和管理定时任务ÿ…...

GridModel事件集合——yonBIP低代码
我们接着看表格相关的事件,用友的文档打不开,真的是天大的404,客观请看这个开发文档网址,找不到了,你说holy 不咯?http://tinper.org/mdf/(如果有哪位小伙伴知道这个地址是不是迁移了的话&#…...
苹果macbook电脑删除数据恢复该怎么做?Mac电脑误删文件的恢复方法
苹果电脑删除数据恢复该怎么做?Mac电脑误删文件的恢复方法 如何在Mac上恢复误删除的文件?在日常使用Mac电脑时,无论是工作还是娱乐,我们都会创建和处理大量的文件。然而,有时候可能会不小心删除一些重要的文件&#x…...

2024年R2移动式压力容器充装证模拟考试题库及R2移动式压力容器充装理论考试试题
题库来源:安全生产模拟考试一点通公众号小程序 2024年R2移动式压力容器充装证模拟考试题库及R2移动式压力容器充装理论考试试题是由安全生产模拟考试一点通提供,R2移动式压力容器充装证模拟考试题库是根据R2移动式压力容器充装最新版教材,R2…...
云开发超多功能工具箱组合微信小程序源码/附带流量主
这是一款云开发超多功能工具箱组合微信小程序源码附带流量主功能,小程序内包含了40余个功能,堪称全能工具箱了,大致功能如下: 证件照制作 | 垃圾分类查询 | 个性签名制作 二维码生成丨文字九宫格 | 手持弹幕丨照片压缩 | 照片编…...

挑战杯 python+深度学习+opencv实现植物识别算法系统
0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 基于深度学习的植物识别算法研究与实现 🥇学长这里给一个题目综合评分(每项满分5分) 难度系数:4分工作量:4分创新点:4分 🧿 更多…...
pytest的常用插件和Allure测试报告
pytest常用插件 pytest-html插件 安装: pip install pytest-html -U 用途: 生成html的测试报告 用法: 在.ini配置文件里面添加 addopts --htmlreport.html --self-contained-html 效果: 执行结果中存在html测试报告路…...
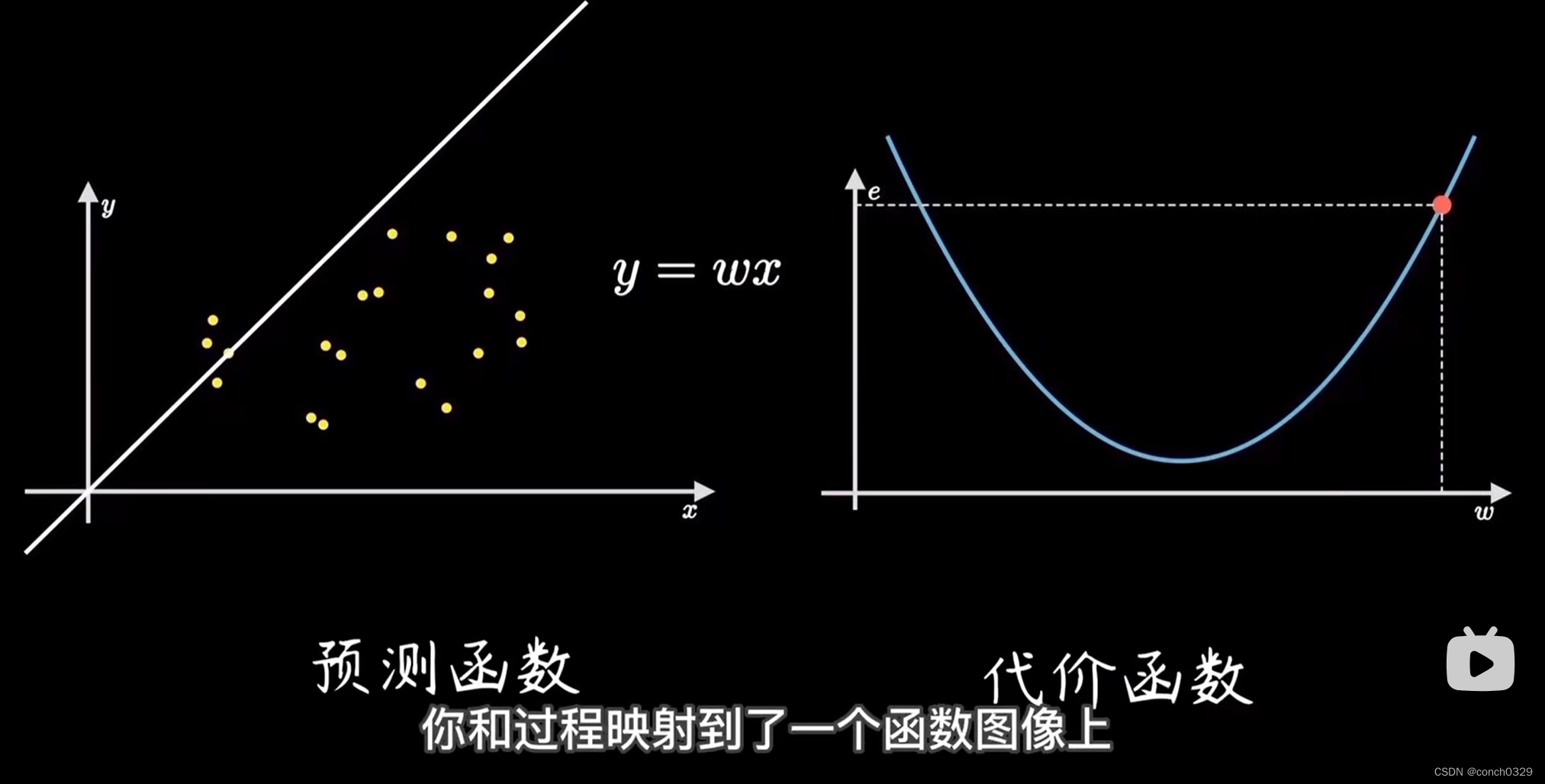
神经网络的权重是什么?
请参考这个视频https://www.bilibili.com/video/BV18P4y1j7uH/?spm_id_from333.788&vd_source1a3cc412e515de9bdf104d2101ecc26a左边是拟合的函数,右边是均方和误差,也就是把左边的拟合函数隐射到了右边,右边是真实值与预测值之间的均方…...

C语言代码 在屏幕上输出9*9乘法口诀表
在屏幕上输出9*9乘法口诀表。 代码示例: #include <stdio.h>int main() {int i 0;for (i 1; i < 9; i)//打印所有行的循环{int j 0;for (j 1; j < i; j)//打印每一行中所有列的循环{printf("%d*%d%-2d ", i, j, i * j);//%-2d的意思是两…...
11.0 Zookeeper watcher 事件机制原理剖析
zookeeper 的 watcher 机制,可以分为四个过程: 客户端注册 watcher。服务端处理 watcher。服务端触发 watcher 事件。客户端回调 watcher。 其中客户端注册 watcher 有三种方式,调用客户端 API 可以分别通过 getData、exists、getChildren …...
HGAME 2024 WEEK 1 :web ezHTTP
题目: 看到这个就知道是文件头伪造 第一想法就是Referer伪造 所以伪造 Referer: vidar.club 然后构造伪造的Referer 然后提示通过那些东西访问页面,User-Agent: 是构造你浏览器访问信息的,所以复制右边那一串替代就好了 然后要求我们从本地…...
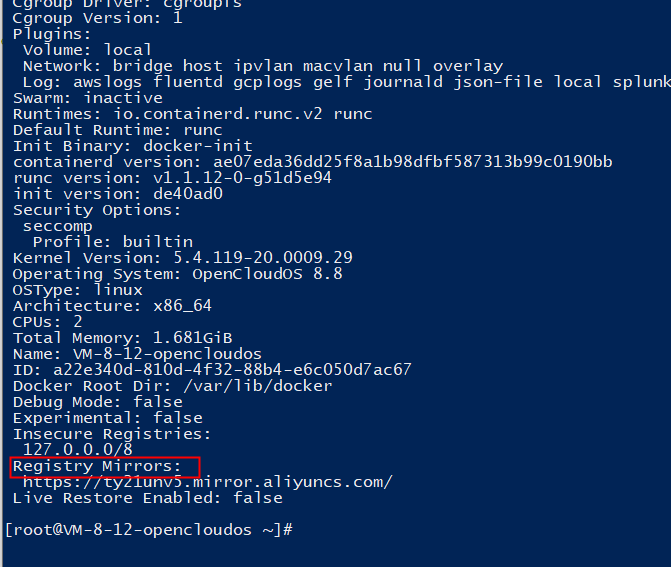
Linux【docker 设置阿里源】
文章目录 一、查看本地docker的镜像配置二、配置阿里镜像三、检查配置 一、查看本地docker的镜像配置 docker info一般没有配置过是不会出现Registry字段的 二、配置阿里镜像 直接执行下面代码即可,安装1.10.0以上版本的Docker客户端都会有/etc/docker 1.建立配置…...

app逆向-frida-rpc详解
Frida-RPC是Frida工具的一个组件,用于在应用程序和Frida脚本之间进行远程过程调用(RPC)。远程过程调用是一种允许应用程序的不同部分或不同的应用程序之间进行通信的方法。在Frida中,RPC通过JavaScript脚本和应用程序之间建立通信…...
复习提纲27)
计算机网络(第六版)复习提纲27
7 TCP流量控制 A 利用滑动窗口实现流量控制 所谓流量控制,就是让发送方发送速率不要太快,让接收方来得及接收 1 利用窗口进行流量控制 2 持续计时器和零窗口探测报文(仅携带一字节的数据) B TCP的传输效率(TCP报文段的…...

解析与模拟常用字符串函数strcpy,strcat,strcmp,strstr(一)
今天也是去学习了一波字符串函数,想着也为了加深记忆,所以写一下这篇博客。既帮助了我也帮助了想学习字符串函数的各位。下面就开始今天的字符串函数的学习吧。 目录 strcpy与strncpy strcat与strncat strcmpy strstr strcpy与strncpy 在 C 语言中&…...

node.js后端+小程序前端+mongoDB(增删改查)
前言 今天我对比了以下node.js的express与python的fastAPI,我决定我还是出一期关于node.jsmangoDB小程序的小案例吧。 不是python的fastAPI不好用,因为fastAPI是python较新的技术,我不敢果断发出教学文章(这件事情还是留着给pyt…...
thinkphp数据批量提交(群发消息)
<form id="edit-form" class="form-horizontal" role="form" data-toggle<...
大华 DSS 数字监控系统 attachment_getAttList.action SQL 注入漏洞复现
0x01 产品简介 大华 DSS 数字监控系统是大华开发的一款安防视频监控系统,拥有实时监视、云台操作、录像回放、报警处理、设备管理等功能。 0x02 漏洞概述 大华 DSS存在SQL注入漏洞,攻击者 /portal/attachment_getAttList.action 路由发送特殊构造的数据包,利用报错注入获…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...
