最大子数组和

一、题目
给你一个整数数组nums,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组[4,-1,2,1]的和最大,为6。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
1 <= nums.length <= 105
-104 <= nums[i] <= 104
进阶: 如果你已经实现复杂度为O(n)的解法,尝试使用更为精妙的 分治法 求解。
二、代码
【1】动态规划: 假设nums数组的长度是n,下标从0到n−1。我们用f(i)代表以第i个数结尾的「连续子数组的最大和」,那么很显然我们要求的答案就是:max0≤i≤n−1{f(i)}因此我们只需要求出每个位置的f(i),然后返回f数组中的最大值即可。那么我们如何求f(i)呢?我们可以考虑nums[i]单独成为一段还是加入f(i−1)对应的那一段,这取决于nums[i]和f(i−1)+nums[i]的大小,我们希望获得一个比较大的,于是可以写出这样的动态规划转移方程:f(i)=max{f(i−1)+nums[i],nums[i]}不难给出一个时间复杂度O(n)、空间复杂度O(n)的实现,即用一个f数组来保存f(i)的值,用一个循环求出所有f(i)。考虑到f(i)只和f(i−1)相关,于是我们可以只用一个变量pre来维护对于当前f(i)的f(i−1)的值是多少,从而让空间复杂度降低到O(1),这有点类似「滚动数组」的思想。
class Solution {public int maxSubArray(int[] nums) {int pre = 0, maxAns = nums[0];for (int x : nums) {pre = Math.max(pre + x, x);maxAns = Math.max(maxAns, pre);}return maxAns;}
}
时间复杂度: O(n),其中n为nums数组的长度。我们只需要遍历一遍数组即可求得答案。
空间复杂度: O(1)。我们只需要常数空间存放若干变量。
【2】分治: 这个分治方法类似于「线段树求解最长公共上升子序列问题」的pushUp操作。 也许读者还没有接触过线段树,没有关系,方法二的内容假设你没有任何线段树的基础。当然,如果读者有兴趣的话,推荐阅读线段树区间合并法解决多次询问的「区间最长连续上升序列问题」和「区间最大子段和问题」,还是非常有趣的。
我们定义一个操作get(a, l, r)表示查询a序列[l,r]区间内的最大子段和,那么最终我们要求的答案就是get(nums, 0, nums.size() - 1)。如何分治实现这个操作呢?对于一个区间[l,r],我们取m=⌊l+r2⌋,对区间[l,m]和[m+1,r]分治求解。当递归逐层深入直到区间长度缩小为1的时候,递归「开始回升」。这个时候我们考虑如何通过[l,m]区间的信息和[m+1,r]区间的信息合并成区间[l,r]的信息。最关键的两个问题是:
1、我们要维护区间的哪些信息呢?
2、我们如何合并这些信息呢?
对于一个区间[l,r],我们可以维护四个量:
1、lSum表示[l,r]内以l为左端点的最大子段和
2、rSum表示[l,r]内以r为右端点的最大子段和
3、mSum表示[l,r]内的最大子段和
4、iSum表示[l,r]的区间和
以下简称[l,m]为[l,r]的「左子区间」,[m+1,r]为[l,r]的「右子区间」。我们考虑如何维护这些量呢(如何通过左右子区间的信息合并得到[l,r]的信息)?对于长度为1的区间[i,i],四个量的值都和nums[i]相等。对于长度大于1的区间:
1、首先最好维护的是iSum,区间[l,r]的iSum就等于「左子区间」的iSum加上「右子区间」的iSum。
2、对于[l,r]的lSum,存在两种可能,它要么等于「左子区间」的lSum,要么等于「左子区间」的iSum加上「右子区间」的lSum,二者取大。
3、对于[l,r]的rSum,同理,它要么等于「右子区间」的rSum,要么等于「右子区间」的iSum加上「左子区间」的rSum,二者取大。
4、当计算好上面的三个量之后,就很好计算[l,r]的mSum了。我们可以考虑[l,r]的mSum对应的区间是否跨越m——它可能不跨越m,也就是说[l,r]的mSum可能是「左子区间」的mSum和 「右子区间」的mSum中的一个;它也可能跨越m,可能是「左子区间」的rSum和 「右子区间」的lSum求和。三者取大。
这样问题就得到了解决。
class Solution {public class Status {public int lSum, rSum, mSum, iSum;public Status(int lSum, int rSum, int mSum, int iSum) {this.lSum = lSum;this.rSum = rSum;this.mSum = mSum;this.iSum = iSum;}}public int maxSubArray(int[] nums) {return getInfo(nums, 0, nums.length - 1).mSum;}public Status getInfo(int[] a, int l, int r) {if (l == r) {return new Status(a[l], a[l], a[l], a[l]);}int m = (l + r) >> 1;Status lSub = getInfo(a, l, m);Status rSub = getInfo(a, m + 1, r);return pushUp(lSub, rSub);}public Status pushUp(Status l, Status r) {int iSum = l.iSum + r.iSum;int lSum = Math.max(l.lSum, l.iSum + r.lSum);int rSum = Math.max(r.rSum, r.iSum + l.rSum);int mSum = Math.max(Math.max(l.mSum, r.mSum), l.rSum + r.lSum);return new Status(lSum, rSum, mSum, iSum);}
}
假设序列a的长度为n。
时间复杂度: 假设我们把递归的过程看作是一颗二叉树的先序遍历,那么这颗二叉树的深度的渐进上界为O(logn),这里的总时间相当于遍历这颗二叉树的所有节点,故总时间的渐进上界是O(∑i=1logn2i−1)=O(n),故渐进时间复杂度为O(n)。
空间复杂度: 递归会使用O(logn)的栈空间,故渐进空间复杂度为O(logn)。
题外话: 「方法二」相较于「方法一」来说,时间复杂度相同,但是因为使用了递归,并且维护了四个信息的结构体,运行的时间略长,空间复杂度也不如方法一优秀,而且难以理解。那么这种方法存在的意义是什么呢?
对于这道题而言,确实是如此的。但是仔细观察「方法二」,它不仅可以解决区间[0,n−1],还可以用于解决任意的子区间[l,r]的问题。如果我们把[0,n−1]分治下去出现的所有子区间的信息都用堆式存储的方式记忆化下来,即建成一棵真正的树之后,我们就可以在O(logn)的时间内求到任意区间内的答案,我们甚至可以修改序列中的值,做一些简单的维护,之后仍然可以在O(logn)的时间内求到任意区间内的答案,对于大规模查询的情况下,这种方法的优势便体现了出来。这棵树就是上文提及的一种神奇的数据结构——线段树。
相关文章:

最大子数组和
一、题目 给你一个整数数组nums,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组 是数组中的一个连续部分。 示例 1: 输入:nums [-2,1,-3,4,-1,2,1,-5,4] 输出&#…...
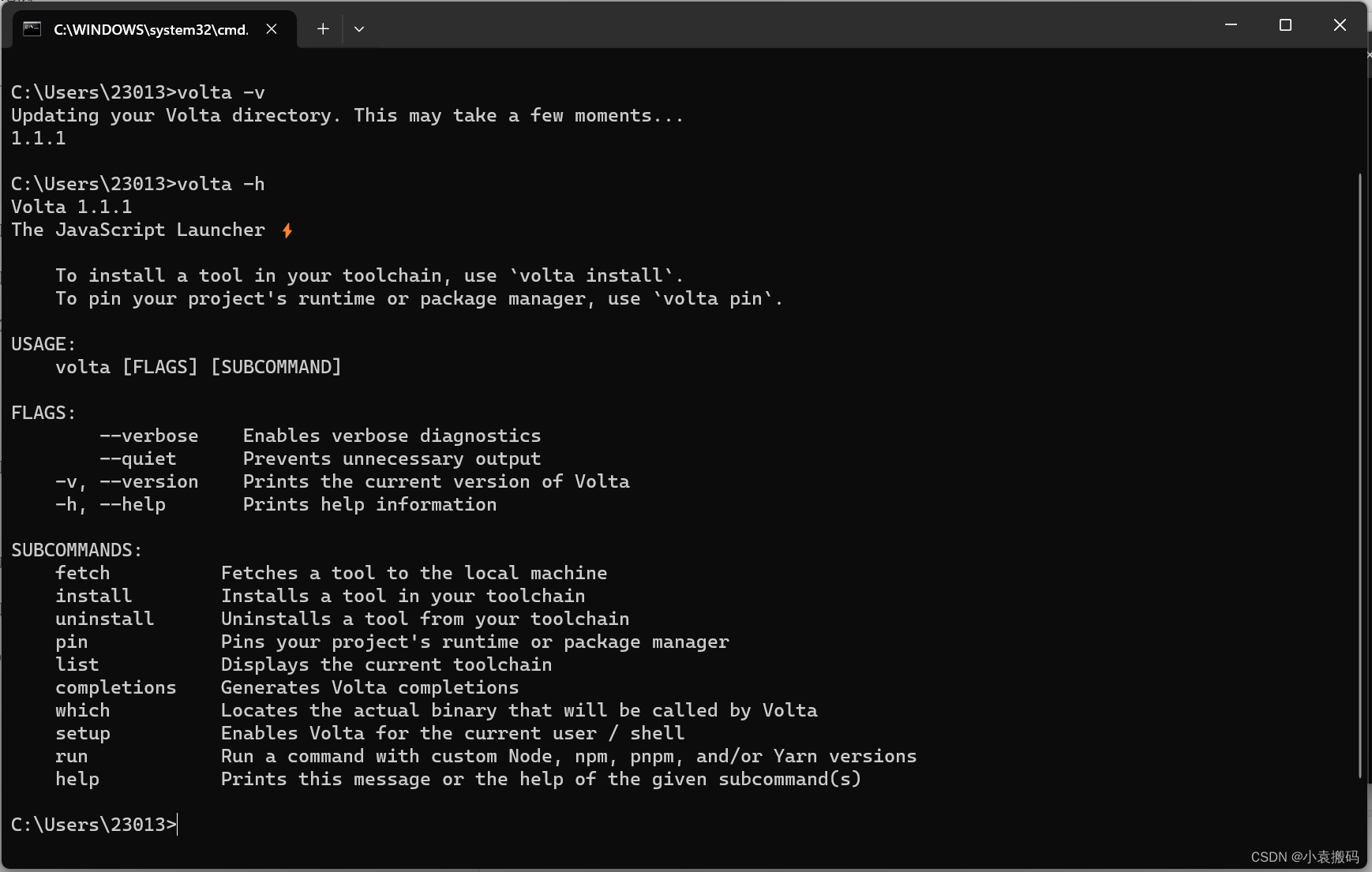
Node.js版本管理工具之_Volta
Node.js包管理工具之_Volta 文章目录 Node.js包管理工具之_Volta1. 官网1. 官网介绍2. 特点1. 快( Fast)2. 可靠(Reliable)3. 普遍( Universal) 2. 下载与安装1. 下载2. 安装3. 查看 3. 使用1. 查看已安装的工具包2. 安装指定的node版本3.切换项目中使用的版本 1. 官网 1. 官网…...

Redis 命令大全
文章目录 启动与连接Key(键)相关命令String(字符串)Hash(哈希)List(列表)Set(集合)Sorted Set(有序集合)其他常见命令HyperLogLog&…...

再这么烂下去,离糊就不远了。别让才华被埋没。
♥ 为方便您进行讨论和分享,同时也为能带给您不一样的参与感。请您在阅读本文之前,点击一下“关注”,非常感谢您的支持! 文 |猴哥聊娱乐 编 辑|徐 婷 校 对|侯欢庭 近日,胡歌凭借电视剧《繁花》荣登《环球银幕》二月…...

Unity BuffSystem buff系统
Unity BuffSystem buff系统 一、介绍二、buff系统架构三、架构讲解四、框架使用buff数据Json数据以及工具ShowTypeBuffTypeMountTypeBuffOverlapBuffShutDownTypeBuffCalculateType时间和层数这里也不过多说明了如何给生物添加buff 五、总结 一、介绍 现在基本做游戏都会需要些…...

Android rom定制 修改system分区的容量大小
1、写在前面 系统ROM定制化,预置app太多,会导致系统rom很大,原生系统system分区已经不够用了,要加大系统systemui分区 2.修改system分区的容量大小的核心类 device/mediatekprojects/$project/BoardConfig.mk build/make/core/Makefile3、修改system 分区的容量大小的核…...

速盾:服务器接入免备案CDN节点的好处有哪些
本文将探讨服务器接入免备案CDN节点的好处,包括提高网站的访问速度、增加网站的稳定性和可靠性、降低带宽成本等方面的优势。同时,还将提供一些相关问题的解答,帮助读者更好地了解这一技术。 随着互联网的迅猛发展,网站的访问速度…...

Redisson看门狗机制
一、背景 网上redis分布式锁的工具方法,大都满足互斥、防止死锁的特性,有些工具方法会满足可重入特性。如果只满足上述3种特性会有哪些隐患呢?redis分布式锁无法自动续期,比如,一个锁设置了1分钟超时释放,…...
)
【Java数据结构】双向 不带头 非循环 链表实现(模拟实现LinkedList类)
LinkedList底层实际上是双向、不带头结点、非循环的链表 链表的分类有八种,常用的有两种:一是单向、不带头结点、非循环的(基本上网上的题型都是这种);二是双向、不带头结点、非循环(LinkedList的底层实现…...
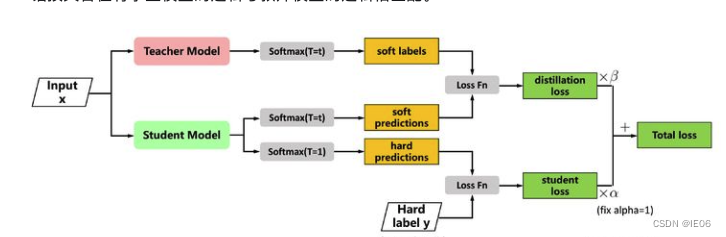
深度学习系列55:深度学习加速技术概述
总体有两个方向:模型优化 / 框架优化 1. 模型优化 1.1 量化 最常见的量化方法为线性量化,权重从float32量化为int8,将输入数据映射在[-128,127]的范围内。在 nvdia gpu,x86、arm 和 部分 AI 芯片平台上,均支持 8bit…...

使用python启动一个roslaunch文件
roslaunch 的实现源码主要位于 ROS 的 ros_comm 仓库中的 tools/roslaunch 目录下。源码主要由 Python 脚本和少量的 C 代码组成。 在Python程序中导入roslaunch包并启动一个ROS launch文件,你需要确保ROS环境已经设置好,并且相关的roslaunch包已经安装…...

JavaEE企业级应用软件开发—Spring框架入门学习笔记(一)
一、认识框架 实际开发中,随着业务的发展,软件系统变得越来越复杂,如果所有的软件都从底层功能开始开发,那将是一个漫长而繁琐的过程。此外,团队协作开发时,由于没有统一的调用规范,系统会出现大…...
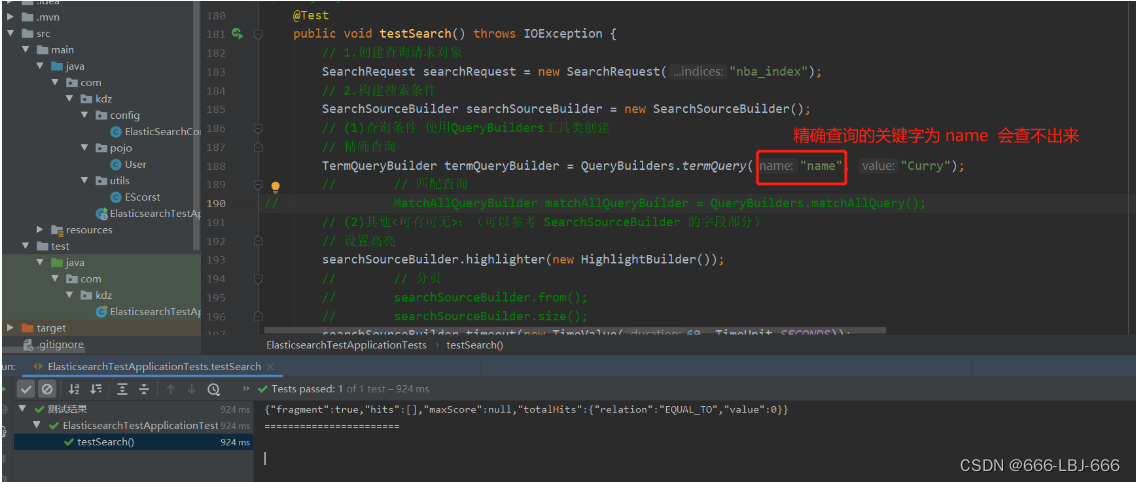
ElasticSearch-SpringBoot整合ElasticSearch
六、SpringBoot整合ElasticSearch 1、浏览官方文档 1、查找跟ES客户端相关的文档 使用Java REST Client 选择Java Hight Level REST Client 2、创建项目的准备 1.找到原生的依赖 2.找到对象 3.分析这个类里面的方法 3、正式创建项目 1.创建工程 2.导入依赖 注意依赖版本…...

用云手机打造tiktok账号需要注意些什么?
随着tiktok平台的火热,越来越多的商家开始尝试更高效的tiktok运营方法。其中,tiktok云手机作为一种新科技引起了很多人的注意,那么用云手机运营tiktok需要注意些什么?下文将对此进行详细解析。 1. 不是所有的云手机都适合做tiktok…...
-数学函数在查询中的应用)
MySQL基础查询篇(9)-数学函数在查询中的应用
在MySQL数据库中,数学函数在查询中扮演了非常重要的角色。这些函数可以帮助我们进行各种数学计算和处理,使得我们能够更有效地处理和分析数据。本文将介绍一些常用的MySQL数学函数及其在查询中的应用。 1. ABS函数 ABS函数用于返回一个数值的绝对值。在…...

c#内置委托
C#语言中有许多内置的委托,其中一些是常用的,包括: Action:表示不带返回值的方法的委托。它可以接受多个参数,但不返回任何值。 Action<int, string> actionDelegate (x, y) > Console.WriteLine("Ac…...

【自动化测试】---Selenium+Java
1.自动化测试分类 接口自动化测试UI自动化测试(移动端自动化测试、Web端自动化测试) 2.选择Selenium作为web自动化工具原因(面试题) 开源免费支持多个浏览器支持多个系统支持多语言Selenium包提供很多供测试使用的API 3.自动化是什…...

uniapp新增一条数据增加一个折叠栏
//折叠栏 <uni-collapse classcollapse refcollapse><uni-collapse-item v-for"(item, index) in dataForm.beefCattleNums" :key"index" :title"item.fatCalfNum" classcollapse-item title-bordershow :borderfalse clicktoggleItem(…...

【Netty技术专题】「原理分析系列」Netty强大特性之Native transports扩展开发实战
Netty强大特性之Native transports技术原理分析 背景介绍JNI概念介绍不同平台的JNI实现 使用Native transports库Maven的分类器(Classifier)使用Linux native transport使用MacOS/BSD native transport库构建native transport库Linux版本要求MacOS/BSD版…...

1-1 动手学深度学习v2-线性回归-笔记
简化核心模型 假设1: 影响房价的关键因素是卧室个数,卫生间个数和居住面积,记为 x 1 x_{1} x1, x 2 x_{2} x2, x 3 x_{3} x3假设2: 成交价是关键因素的加权和 y w 1 x 1 w 2 x 2 w 3 x 3 b yw_{1}x_{1}w_{2}x_{2}w_{3…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

构建Docker镜像的Dockerfile文件详解
文章目录 前言Dockerfile 案例docker build1. 基本构建2. 指定 Dockerfile 路径3. 设置构建时变量4. 不使用缓存5. 删除中间容器6. 拉取最新基础镜像7. 静默输出完整示例 docker runDockerFile 入门syntax指定构造器FROM基础镜像RUN命令注释COPY复制ENV设置环境变量EXPOSE暴露端…...
uni-app学习笔记二十七--设置底部菜单TabBar的样式
官方文档地址:uni.setTabBarItem(OBJECT) | uni-app官网 uni.setTabBarItem(OBJECT) 动态设置 tabBar 某一项的内容,通常写在项目的App.vue的onLaunch方法中,用于项目启动时立即执行 重要参数: indexnumber是tabBar 的哪一项&…...
