1-1 动手学深度学习v2-线性回归-笔记
简化核心模型
- 假设1: 影响房价的关键因素是卧室个数,卫生间个数和居住面积,记为 x 1 x_{1} x1, x 2 x_{2} x2, x 3 x_{3} x3
- 假设2: 成交价是关键因素的加权和
y = w 1 x 1 + w 2 x 2 + w 3 x 3 + b y=w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3}+b y=w1x1+w2x2+w3x3+b权重和偏差的实际值在后面决定
线性一般模型
- 给定 n n n维输入 x = [ x 1 , x 2 , . . . , x n ] T \pmb{x}=[x_{1},x_{2},...,x_{n}]^{T} x=[x1,x2,...,xn]T
(这里 x 1 , x 2 , . . . , x n x_{1},x_{2},...,x_{n} x1,x2,...,xn是实数/标量, [ x 1 , x 2 , . . . , x n ] [x_{1},x_{2},...,x_{n}] [x1,x2,...,xn]是行向量,再一转置就是一个列向量 x = [ x 1 , x 2 , . . . , x n ] T \pmb{x}=[x_{1},x_{2},...,x_{n}]^{T} x=[x1,x2,...,xn]T) - 线性模型有一个 n n n维权重和一个标量偏差
w = [ w 1 , w 2 , . . . , w n ] T , b \pmb{w}=[w_{1},w_{2},...,w_{n}]^{T},b w=[w1,w2,...,wn]T,b( w \pmb{w} w同 x \pmb{x} x理,b是实数/标量) - 输出是输入的加权和
y = w 1 x 1 + w 2 x 2 + . . . + w n x n + b y=w_{1}x_{1}+w_{2}x_{2}+...+w_{n}x_{n}+b y=w1x1+w2x2+...+wnxn+b向量版本: y = ⟨ w , x ⟩ + b y=\langle\pmb{w},\pmb{x}\rangle+b y=⟨w,x⟩+b
( ⟨ w , x ⟩ \langle\pmb{w},\pmb{x}\rangle ⟨w,x⟩表示内积,这里即两个列向量按位相乘。内积算出来的是一个实数标量。)
衡量预测质量
- 比较真实值和预估值,例如房屋售价和估价
- 假设 y y y是真实值, y ^ \hat{y} y^是估计值,我们可以比较
ℓ ( y , y ^ ) = 1 2 ( y − y ^ ) 2 \ell(y,\hat{y})=\frac{1}{2}(y-\hat{y})^{2} ℓ(y,y^)=21(y−y^)2这个叫做平方损失,这里之所以有个 1 2 \frac{1}{2} 21,是因为我们可以在后面的求导过程中很方便地消除掉。
训练数据
- 收集一些数据点来决定参数值(权重和偏差),例如过去6个月卖的房子
- 这被称之为训练数据
- 通常越多越好
- 假设我们有 n n n个样本,记
X = [ x 1 , x 2 , . . . , x n ] T \pmb{X}=[\pmb{x_{1}},\pmb{x_{2}},...,\pmb{x_{n}}]^{T} X=[x1,x2,...,xn]T(假设每个 x i \pmb{x_{i}} xi都是按照上面模型定义的列向量(一个列向量就是一个样本),我们把样本一列列的排好,再经过一个转置,最后的效果就是原先的每一列现在到了每一行, X \pmb{X} X的每一行都是一个样本。)
y = [ y 1 , y 2 , . . . , y n ] T \pmb{y}=[y_{1},y_{2},...,y_{n}]^{T} y=[y1,y2,...,yn]T
(每一个 y i y_{i} yi都是一个实数的数值,也即一个样本,那么 y \pmb{y} y就是一个列向量。)
参数学习
-
训练损失
关于数据 X \pmb{X} X, y \pmb{y} y,权重 w \pmb{w} w,偏差 b b b的损失函数(真实值-估计值):(这里算出来的是个标量)
ℓ ( X , y , w , b ) = 1 2 n ∑ i = 1 n ( y i − ⟨ x i , w ⟩ − b ) 2 = 1 2 n ∣ ∣ y − X w − b ∣ ∣ 2 \ell(\pmb{X},\pmb{y},\pmb{w},b)=\frac{1}{2n}\sum_{i=1}^{n}(y_{i}-\langle\pmb{x_{i},w}\rangle-b)^{2}=\frac{1}{2n}||\pmb{y}-\pmb{Xw}-b||^{2} ℓ(X,y,w,b)=2n1i=1∑n(yi−⟨xi,w⟩−b)2=2n1∣∣y−Xw−b∣∣2在数学中,双竖线 ∣∣⋅∣∣ 通常表示向量的范数(norm),是衡量向量大小的一种方法。在计算线性回归模型的训练损失时,这个符号用来表示预测误差向量的欧几里得范数(Euclidean norm),也就是通常所说的 L2 范数。
L2范数(L2 norm),是向量元素的平方和的平方根。它在数学和机器学习中经常被用作一种正则化项、距离度量或误差度量。
∣ ∣ x ∣ ∣ 2 = ( x 1 2 + x 2 2 + . . . + x n 2 ) 1 2 ||x||_{2} = (x_{1}^{2} + x_{2}^{2} + ... + x_{n}^{2})^{\frac{1}{2}} ∣∣x∣∣2=(x12+x22+...+xn2)21这里的 ∣ ∣ y − X w − b ∣ ∣ 2 ||\pmb{y}-\pmb{Xw}-b||^{2} ∣∣y−Xw−b∣∣2 表示的是预测误差向量 y − X w − b \pmb{y}-\pmb{Xw}-b y−Xw−b 的 L2 范数的平方,其中 y \pmb{y} y 是实际值的向量, X \pmb{X} X 是特征矩阵, w \pmb{w} w 是权重向量, b b b 是偏差项。
计算L2范数的平方是将每个样本的损失值平方后求和,再除以 2 n 2n 2n,这样做的目的是平均损失,并且在后续的优化过程中,平方项可以帮助计算梯度。
两个等号,后一个是用向量的形式来表示,但是意义都是一样的,也即都是在先计算样本损失值的平方和,再除以样本数,得到一个对于所有样本来说的平均损失。
对于向量的形式,更易于并行化。 -
最小化损失来学习参数 w ∗ , b ∗ = a r g min w , b ℓ ( X , y , w , b ) \pmb{w^{*},b^{*}}=arg\;\min_{\pmb{w},b}\ell(\pmb{X},\pmb{y},\pmb{w},b) w∗,b∗=argw,bminℓ(X,y,w,b)
这个公式的意思是说:要找到 w \pmb{w} w和 b b b的那个具体值 或者 值的组合 w ∗ , b ∗ \pmb{w^{*},b^{*}} w∗,b∗,使得 ℓ ( X , y , w , b ) \ell(\pmb{X},\pmb{y},\pmb{w},b) ℓ(X,y,w,b)达到最小值。
这里的 “arg min” 是 “argument of the minimum” 的缩写。
显示解
- 将偏差加入权重
X ← [ X , 1 ] w ← [ w b ] \pmb{X}\leftarrow [\pmb{X},\pmb{1}] \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \pmb{w}\leftarrow\left [ \begin{matrix} \pmb{w} \\ b \\ \end{matrix} \right ] X←[X,1] w←[wb] 给 X \pmb{X} X加一列全 1 1 1的特征,也就是在末尾加一个全 1 1 1的列向量 1 \pmb{1} 1,相当于是给所有样本新增一个为1的实数项,然后把偏差放到权重的最后一行。相当于是把偏差融进数据 X \pmb{X} X和权重 w \pmb{w} w。
损失函数变为:
ℓ ( X , y , w ) = 1 2 n ∣ ∣ y − X w ∣ ∣ 2 ∂ ∂ w ℓ ( X , y , w ) = 1 n ( y − X w ) T X \ell(\pmb{X},\pmb{y},\pmb{w})=\frac{1}{2n}||\pmb{y}-\pmb{Xw}||^{2}\ \ \ \ \ \ \ \ \ \ \frac{\partial }{\partial \pmb{w}}\ell(\pmb{X},\pmb{y},\pmb{w})=\frac{1}{n}(\pmb{y}-\pmb{Xw})^{T}\pmb{X} ℓ(X,y,w)=2n1∣∣y−Xw∣∣2 ∂w∂ℓ(X,y,w)=n1(y−Xw)TX - 线性模型的损失是凸函数,所以最优解满足
∂ ∂ w ℓ ( X , y , w ) = 0 \frac{\partial }{\partial \pmb{w}}\ell(\pmb{X},\pmb{y},\pmb{w})=0 ∂w∂ℓ(X,y,w)=0 ⇔ 1 n ( y − X w ) T X = 0 \Leftrightarrow \frac{1}{n}(\pmb{y}-\pmb{Xw})^{T}\pmb{X}=0 ⇔n1(y−Xw)TX=0 ⇔ w ∗ = ( X T X ) − 1 X y \Leftrightarrow \pmb{w^{*}}=(\pmb{X}^{T}\pmb{X})^{-1}\pmb{X}\pmb{y} ⇔w∗=(XTX)−1Xy凸函数(Convex function)是指从函数图形上来看,任意两点连成的线段,皆位于图形的上方的实值函数。
凸函数的最优解是满足使得它的梯度等于0的地方。
总结
- 线性回归是对 n n n维输入的加权,外加偏差( y ^ = X w + b \hat{y}=\pmb{Xw}+b y^=Xw+b)
- 使用平方损失来衡量预测值和真实值的差异
- 线性回归有显示解
- 线性回归可以看作单层神经网络,是最简单的神经网络
QA补充
-
为啥使用平方损失而不是绝对差值?
绝对差值在零点处的导数比较难求,并不是一个处处可导的函数 -
为啥损失要求平均?
求平均和不求平均区别不大,但是不求的话,会导致梯度比较大,如果不除以 n n n的话,就把学习率除以 n n n吧。
除以 n n n的好处是:不管你的样本多大,批量多大,我的梯度都差不多,使得我调学习率比较容易,比较好调。
相关文章:

1-1 动手学深度学习v2-线性回归-笔记
简化核心模型 假设1: 影响房价的关键因素是卧室个数,卫生间个数和居住面积,记为 x 1 x_{1} x1, x 2 x_{2} x2, x 3 x_{3} x3假设2: 成交价是关键因素的加权和 y w 1 x 1 w 2 x 2 w 3 x 3 b yw_{1}x_{1}w_{2}x_{2}w_{3…...
算法每日一题: 使用循环数组所有元素相等的最少秒数 | 哈希
大家好,我是星恒,今天给大家带来的是一道需要感觉规律的题目,只要读懂题目中的规律,就可以做出来了 这道题用到了哈希,还有一个关键点比较类似循环队列 题目:leetcode 2808 给你一个下标从 0 开始长度为 n…...
canvas实现涂鸦画板功能
查看专栏目录 canvas实例应用100专栏,提供canvas的基础知识,高级动画,相关应用扩展等信息。canvas作为html的一部分,是图像图标地图可视化的一个重要的基础,学好了canvas,在其他的一些应用上将会起到非常重…...

6-3、T型加减速单片机程序【51单片机+L298N步进电机系列教程】
↑↑↑点击上方【目录】,查看本系列全部文章 摘要:根据前两节内容,已完成所有计算工作,本节内容介绍具体单片机程序流程及代码 一、程序流程图 根据前两节文章内容可知,T型加减速的关键内容是运动类型的判断以及定时…...
Flutter组件 StatefulWidget、StatelessWidget 可继承写法
前言 学过Java的同学,应该都知道面向对象语言的三大特征,封装、继承、多态; Dart也是面向对象的语言,但是在Flutter中的很多组件都被下划线 _ 标记为私有,导致无法继承,本文将介绍一种非私有的创建组件写…...
skywalking链路追踪
skywalking 1.简介1.1 skywalking介绍1.2 链路追踪框架对比1.3 Skywalking架构 2 环境构建2.1 windows环境2.1.1 启动skywalking服务和UI界面2.1.2 在IDEA启动项目中使用Skywalking2.1.3 skywalking持久化 2.2 linux环境 1.简介 微服务架构已经是一个很通用的系统架构…...
如何在苹果Mac上进行分屏,多任务处理?
Apple 在 macOS Catalina 中引入了 Split View,让您可以同时查看两个应用程序。如果同时处理多个应用程序,但在它们之间切换时感到沮丧,小编教给大家在 Macbook Pro/Air 或 iMac 上使用分屏功能流畅地进行多任务处理。 注意:您可…...

【Java EE】----Spring框架创建和使用
1.Spring框架创建 创建一个maven项目 添加Spring框架支持 <dependencies> 上下文<dependency><groupId>org.springframework</groupId><artifactId>spring-context</artifactId><version>5.2.3.RELEASE</version></depende…...
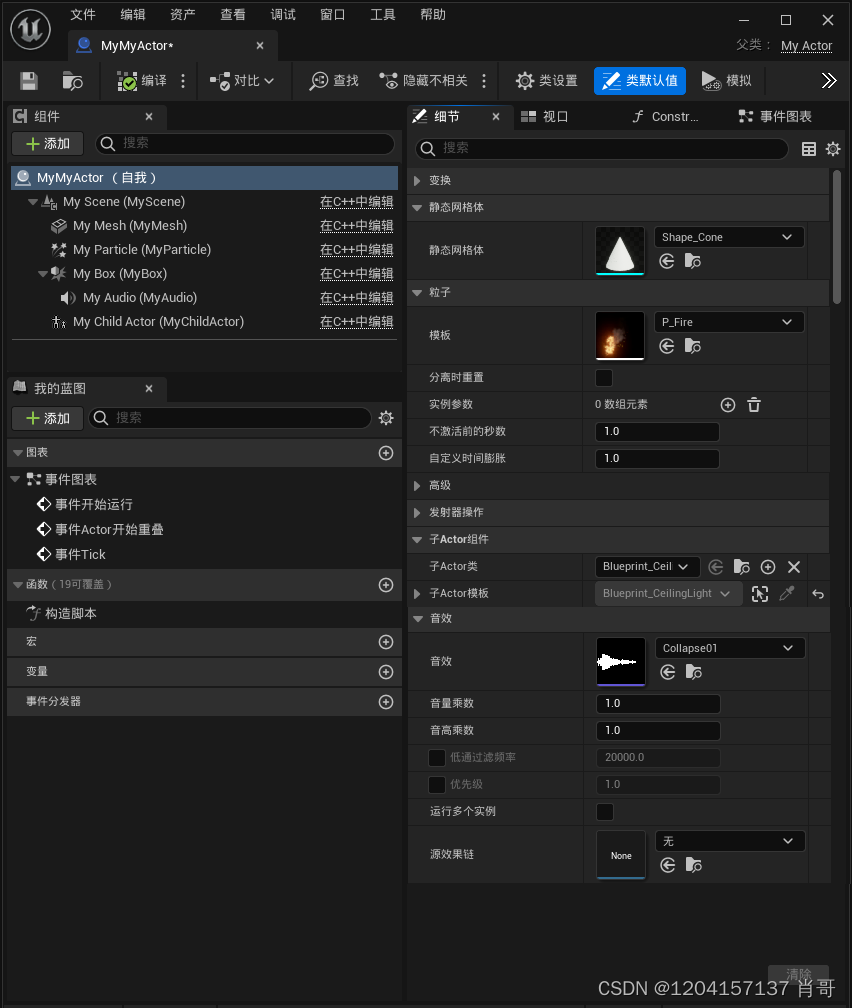
UE4 C++ 静态加载类和资源
静态加载类和资源:指在编译时加载,并且只能在构造函数中编写代码 .h //增加所需组件的头文件 #include "Components/SceneComponent.h" //场景组件 #include "Components/StaticMeshComponent.h" //静态网格体组件 #include &qu…...
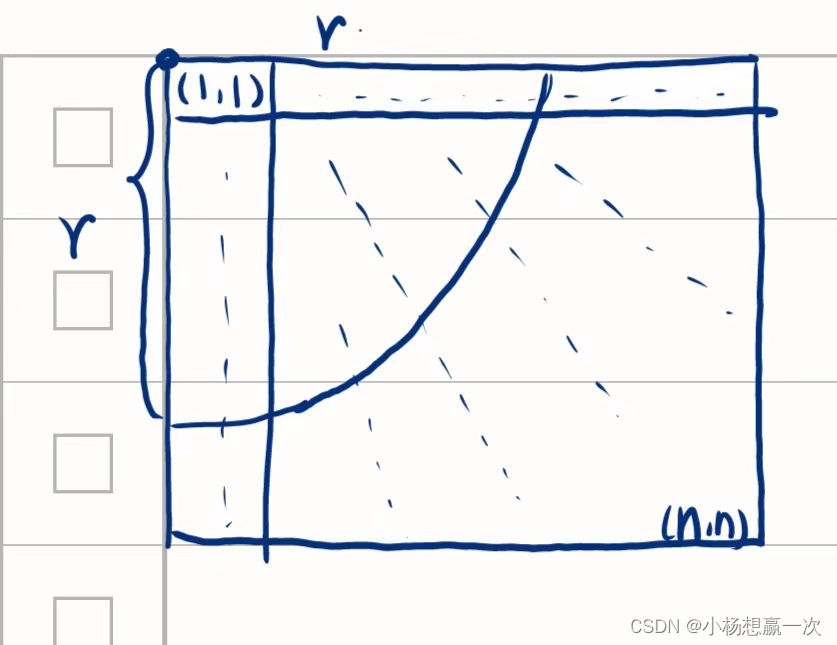
洛谷C++简单题小练习day9—[AHOI2017]寻找探监点
day9--[AHOI2017]寻找探监点--2.7 习题概述 题目描述 一个nn 的网格图(标号由 1,1 开始)上有 m 个探测器,每个探测器有个探测半径 r ,问这 nn 个点中有多少个点能被探测到。 输入格式 第一行 3 个整数 n,m,r。 接下来 m 行&…...
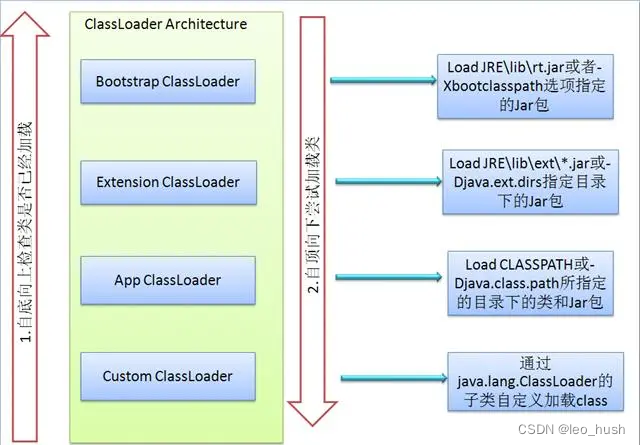
JVM双亲委派机制
双亲委派模型是一种组织类加载器之间关系的一种规范,他的工作原理是:如果一个类加载器收到了类加载的请求,它不会自己去尝试加载这个类,而是把这个请求委派给父类加载器去完成,这样层层递进,最终所有的加载请求都被传到最顶层的启动类加载器中,只有当父类加载器无法完成这个加载…...
思科模拟器实验合集
目 录 实验一 常用网络命令的使用.................................... 1 实验二 双绞线制作.................................................. 12 实验三 网络模拟软件.............................................. 15 实验四 交换机基本配置..................…...
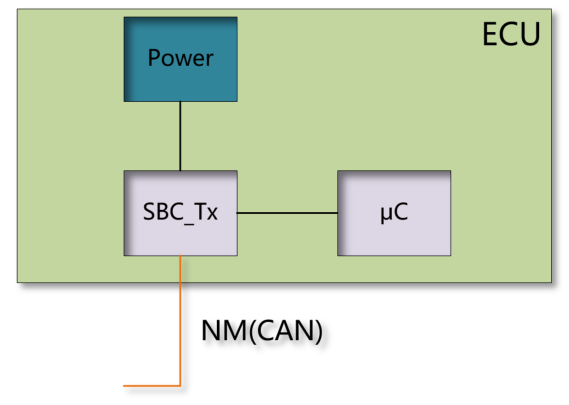
18.AUTOSAR 网络管理系统(一)
目录 1.为什么需要整车网络管理 2.本地唤醒和网络唤醒 3.小结 1.为什么需要整车网络管理 在描述AUTOSAR网络管理细节前,大家可以思考几个问题: 1.网络管理为整车系统提供了什么样的服务? 2.整车网络视角看,每个ECU的上下电是…...

802.11 MAC帧介绍
控制帧 RTS(Request To Send):用于申请无线媒介的使用时间CTS(Clear To Send):用于回复RTS帧ACK:对MAC帧的肯定确认PS-POLL:STA用于从AP中获取因省电模式而缓存的数据,只…...

【高阶数据结构】B-树详解
文章目录 1. 常见的搜索结构2. 问题提出使用平衡二叉树搜索树的缺陷使用哈希表的缺陷 3. B-树的概念4. B-树的插入分析插入过程分析插入过程总结 5. B-树的代码实现5.1 B-树的结点设计5.2 B-树的查找5.3 B-树的插入实现InsertKey插入和分裂测试 6. B-树的删除(思想&…...
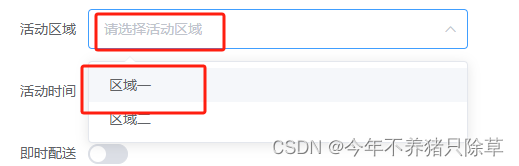
elementui常用组件-个人版(间断更新)
Dialog 对话框 el-dialog <el-dialogtitle"提示":visible.sync"dialogVisible"width"30%":before-close"handleClose"><span>这是一段信息</span><span slot"footer" class"dialog-footer"…...

无人机在化工消防救援中的应用,消防无人机应用场景分析
火灾对社会环境具有较大影响,因此需要重视消防灭火救援工作,注重现代化技术的运用,将无人机应用到救援过程并保障其应用质量。无人机是一项重要技术,便于消防灭火救援操作,使救援过程灵活展开,排除不利影响…...

java设计模式- 建造者模式
一 需求以及实现方式 1.1 需求描述 我们要创建一个表示汽车的复杂对象,汽车包含发动机、轮胎和座椅等部分。用传统方式创建,代码如下 1.2 传统实现方式 1.抽象类 public abstract class BuildCarAbstaract {//引擎public abstract void buildEng…...
【C++航海王:追寻罗杰的编程之路】类与对象你学会了吗?(下)
目录 1 -> 再谈构造函数1.1 -> 构造函数体赋值1.2 -> 初始化列表1.3 -> explicit关键字 2 -> static成员2.1 -> 概念2.2 -> 特性 3 -> 友元3.1 -> 友元函数3.2 -> 友元类 4 -> 内部类5 -> 匿名对象6 -> 拷贝对象时的一些编译器优化 1 -…...

解决TSP旅行商问题3个可以用Python编程的优化路径算法
旅行商问题(Traveling Salesman Problem, TSP)是一个经典的组合优化问题,它要求找到访问一系列城市并返回起点的最短可能路线,同时每个城市仅访问一次。这个问题是NP-hard的,意味着没有已知的多项式时间复杂度的精确算…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
