算法每日一题: 使用循环数组所有元素相等的最少秒数 | 哈希
大家好,我是星恒,今天给大家带来的是一道需要感觉规律的题目,只要读懂题目中的规律,就可以做出来了
这道题用到了哈希,还有一个关键点比较类似循环队列
题目:leetcode 2808
给你一个下标从 0 开始长度为 n 的数组 nums 。
每一秒,你可以对数组执行以下操作:
- 对于范围在 [0, n - 1] 内的每一个下标 i ,将 nums[i] 替换成 nums[i] ,nums[(i - 1 + n) % n] 或者 nums[(i + 1) % n] 三者之一。
注意,所有元素会被同时替换。
请你返回将数组 nums 中所有元素变成相等元素所需要的 最少 秒数。
示例 1:
输入:nums = [1,2,1,2]
输出:1
解释:我们可以在 1 秒内将数组变成相等元素:
- 第 1 秒,将每个位置的元素分别变为 [nums[3],nums[1],nums[3],nums[3]] 。变化后,nums = [2,2,2,2] 。
1 秒是将数组变成相等元素所需要的最少秒数。
示例 2:
输入:nums = [2,1,3,3,2]
输出:2
解释:我们可以在 2 秒内将数组变成相等元素:
- 第 1 秒,将每个位置的元素分别变为 [nums[0],nums[2],nums[2],nums[2],nums[3]] 。变化后,nums = [2,3,3,3,3] 。
- 第 2 秒,将每个位置的元素分别变为 [nums[1],nums[1],nums[2],nums[3],nums[4]] 。变化后,nums = [3,3,3,3,3] 。
2 秒是将数组变成相等元素所需要的最少秒数。
示例 3:
输入:nums = [5,5,5,5]
输出:0
解释:不需要执行任何操作,因为一开始数组中的元素已经全部相等。
提示:
- 1 <= n == nums.length <= 105
- 1 <= nums[i] <= 109
分析:
阅读题目,大家首先可能对这两个式子有些迷惑:nums[(i - 1 + n) % n] 和 nums[(i + 1) % n]
其实他们就是处理了一下首尾元素:
nums[(i - 1 + n) % n]:当元素为首元素时(下标为0),式子变为了nums[n - 1];其他元素相当于nums[i - 1]nums[(i + 1) % n]:当元素为尾元素时(下标为n - 1),式子变为了nums[0];其他元素相当于nums[i + 1]
这样做的目的是可以让首尾相连,感觉首元素和尾元素相邻了
好,知道了这个,我们正式开始分析这道题目:
读题,我们可以知道,一个元素,一次可以将相邻的两个元素下标变为自己的,所以每一秒我们可以影响相邻元素。
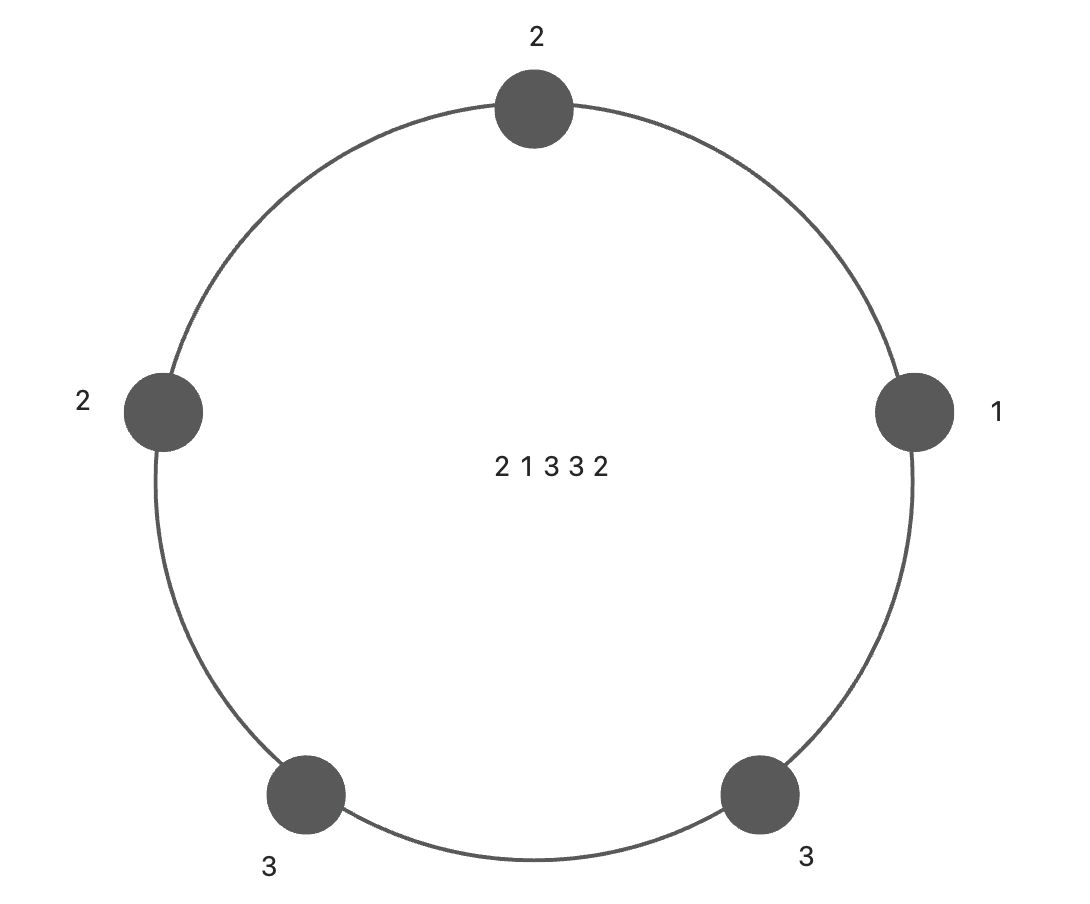
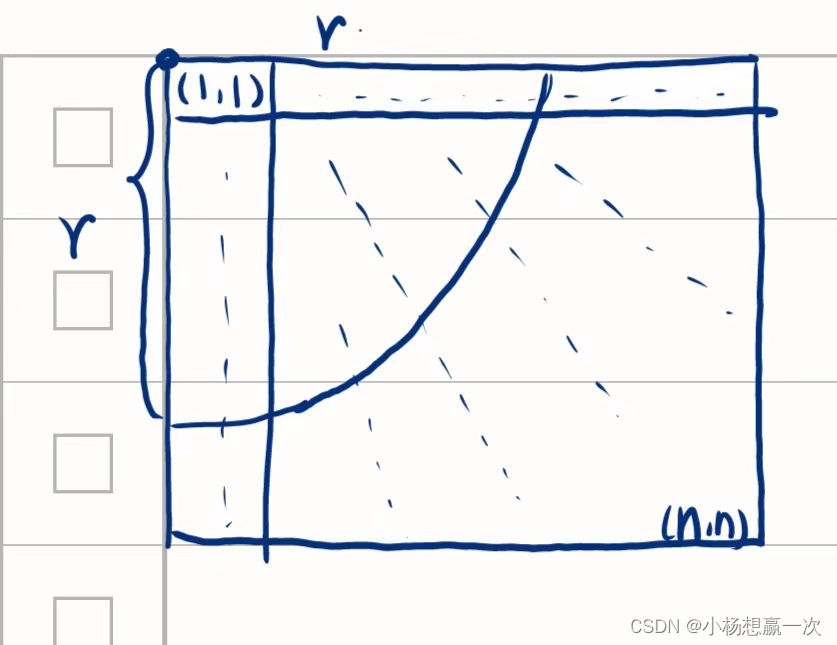
结合上面的理论,我们来看这个图
也就是说,变成相等元素所需要的 最少 秒数,就是两个相邻相同元素的 最大 距离 / 2
注意,首尾距离也要计算
至于我们选择哪个作为相同元素更好,我们只要将每一种元素的所需最大秒数求出来比较就可以了
我们来看题解:
题解:
class Solution {public int minimumSeconds(List<Integer> nums) {HashMap<Integer, List<Integer>> mp = new HashMap<>();int n = nums.size(), res = n;for (int i = 0; i < n; ++i) {mp.computeIfAbsent(nums.get(i), k -> new ArrayList<>()).add(i);}for (List<Integer> positions : mp.values()) {int mx = positions.get(0) + n - positions.get(positions.size() - 1);for (int i = 1; i < positions.size(); ++i) {mx = Math.max(mx, positions.get(i) - positions.get(i - 1));}res = Math.min(res, mx / 2);}return res;}
}
注意:
mp.computeIfAbsent(nums.get(i), k -> new ArrayList<>()).add(i);的意思表示key为“i”的键值对是否存在
- 如果存在则获取i的值,并操作值的list添加数据“i"。
- 如果不存在,则调用方法,新创建list结构,将"i"添加到list中,再存入到hashMap中。
- – 这个API适合用于值为集合的
values(): 返回Map集合中所有value组成的以Collection数据类型格式数据。
如果大家有什么思考和问题,可以在评论区讨论,也可以私信我,很乐意为大家效劳。
好啦,今天的每日一题到这里就结束了,如果大家觉得有用,可以可以给我一个小小的赞呢,我们下期再见!
相关文章:

算法每日一题: 使用循环数组所有元素相等的最少秒数 | 哈希
大家好,我是星恒,今天给大家带来的是一道需要感觉规律的题目,只要读懂题目中的规律,就可以做出来了 这道题用到了哈希,还有一个关键点比较类似循环队列 题目:leetcode 2808 给你一个下标从 0 开始长度为 n…...
canvas实现涂鸦画板功能
查看专栏目录 canvas实例应用100专栏,提供canvas的基础知识,高级动画,相关应用扩展等信息。canvas作为html的一部分,是图像图标地图可视化的一个重要的基础,学好了canvas,在其他的一些应用上将会起到非常重…...

6-3、T型加减速单片机程序【51单片机+L298N步进电机系列教程】
↑↑↑点击上方【目录】,查看本系列全部文章 摘要:根据前两节内容,已完成所有计算工作,本节内容介绍具体单片机程序流程及代码 一、程序流程图 根据前两节文章内容可知,T型加减速的关键内容是运动类型的判断以及定时…...
Flutter组件 StatefulWidget、StatelessWidget 可继承写法
前言 学过Java的同学,应该都知道面向对象语言的三大特征,封装、继承、多态; Dart也是面向对象的语言,但是在Flutter中的很多组件都被下划线 _ 标记为私有,导致无法继承,本文将介绍一种非私有的创建组件写…...
skywalking链路追踪
skywalking 1.简介1.1 skywalking介绍1.2 链路追踪框架对比1.3 Skywalking架构 2 环境构建2.1 windows环境2.1.1 启动skywalking服务和UI界面2.1.2 在IDEA启动项目中使用Skywalking2.1.3 skywalking持久化 2.2 linux环境 1.简介 微服务架构已经是一个很通用的系统架构…...
如何在苹果Mac上进行分屏,多任务处理?
Apple 在 macOS Catalina 中引入了 Split View,让您可以同时查看两个应用程序。如果同时处理多个应用程序,但在它们之间切换时感到沮丧,小编教给大家在 Macbook Pro/Air 或 iMac 上使用分屏功能流畅地进行多任务处理。 注意:您可…...

【Java EE】----Spring框架创建和使用
1.Spring框架创建 创建一个maven项目 添加Spring框架支持 <dependencies> 上下文<dependency><groupId>org.springframework</groupId><artifactId>spring-context</artifactId><version>5.2.3.RELEASE</version></depende…...
UE4 C++ 静态加载类和资源
静态加载类和资源:指在编译时加载,并且只能在构造函数中编写代码 .h //增加所需组件的头文件 #include "Components/SceneComponent.h" //场景组件 #include "Components/StaticMeshComponent.h" //静态网格体组件 #include &qu…...
洛谷C++简单题小练习day9—[AHOI2017]寻找探监点
day9--[AHOI2017]寻找探监点--2.7 习题概述 题目描述 一个nn 的网格图(标号由 1,1 开始)上有 m 个探测器,每个探测器有个探测半径 r ,问这 nn 个点中有多少个点能被探测到。 输入格式 第一行 3 个整数 n,m,r。 接下来 m 行&…...
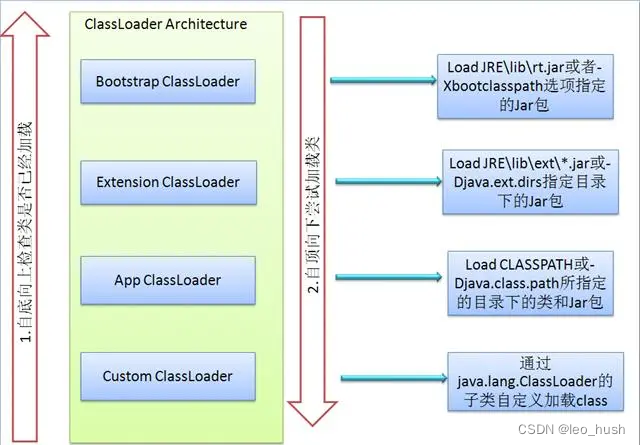
JVM双亲委派机制
双亲委派模型是一种组织类加载器之间关系的一种规范,他的工作原理是:如果一个类加载器收到了类加载的请求,它不会自己去尝试加载这个类,而是把这个请求委派给父类加载器去完成,这样层层递进,最终所有的加载请求都被传到最顶层的启动类加载器中,只有当父类加载器无法完成这个加载…...
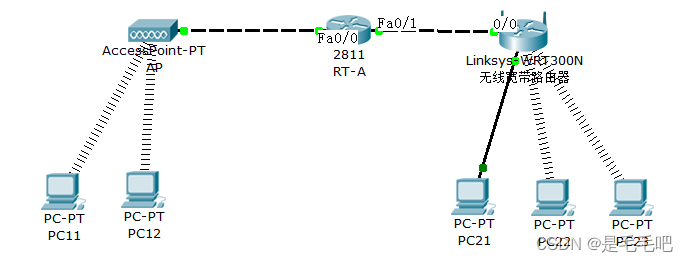
思科模拟器实验合集
目 录 实验一 常用网络命令的使用.................................... 1 实验二 双绞线制作.................................................. 12 实验三 网络模拟软件.............................................. 15 实验四 交换机基本配置..................…...
18.AUTOSAR 网络管理系统(一)
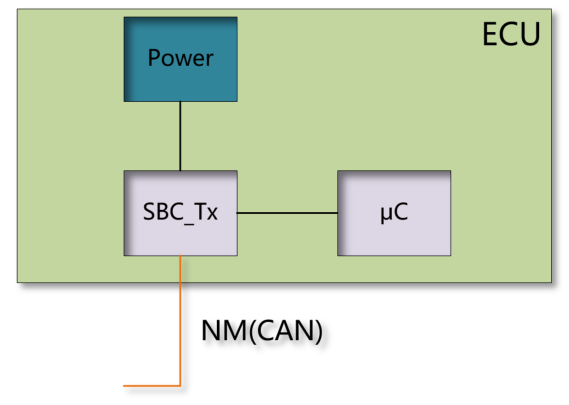
目录 1.为什么需要整车网络管理 2.本地唤醒和网络唤醒 3.小结 1.为什么需要整车网络管理 在描述AUTOSAR网络管理细节前,大家可以思考几个问题: 1.网络管理为整车系统提供了什么样的服务? 2.整车网络视角看,每个ECU的上下电是…...

802.11 MAC帧介绍
控制帧 RTS(Request To Send):用于申请无线媒介的使用时间CTS(Clear To Send):用于回复RTS帧ACK:对MAC帧的肯定确认PS-POLL:STA用于从AP中获取因省电模式而缓存的数据,只…...

【高阶数据结构】B-树详解
文章目录 1. 常见的搜索结构2. 问题提出使用平衡二叉树搜索树的缺陷使用哈希表的缺陷 3. B-树的概念4. B-树的插入分析插入过程分析插入过程总结 5. B-树的代码实现5.1 B-树的结点设计5.2 B-树的查找5.3 B-树的插入实现InsertKey插入和分裂测试 6. B-树的删除(思想&…...
elementui常用组件-个人版(间断更新)
Dialog 对话框 el-dialog <el-dialogtitle"提示":visible.sync"dialogVisible"width"30%":before-close"handleClose"><span>这是一段信息</span><span slot"footer" class"dialog-footer"…...

无人机在化工消防救援中的应用,消防无人机应用场景分析
火灾对社会环境具有较大影响,因此需要重视消防灭火救援工作,注重现代化技术的运用,将无人机应用到救援过程并保障其应用质量。无人机是一项重要技术,便于消防灭火救援操作,使救援过程灵活展开,排除不利影响…...

java设计模式- 建造者模式
一 需求以及实现方式 1.1 需求描述 我们要创建一个表示汽车的复杂对象,汽车包含发动机、轮胎和座椅等部分。用传统方式创建,代码如下 1.2 传统实现方式 1.抽象类 public abstract class BuildCarAbstaract {//引擎public abstract void buildEng…...
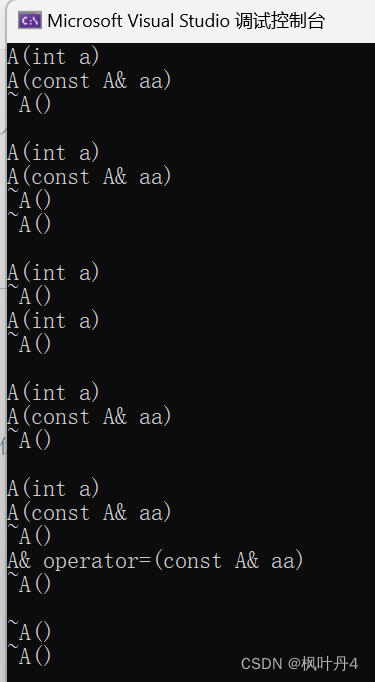
【C++航海王:追寻罗杰的编程之路】类与对象你学会了吗?(下)
目录 1 -> 再谈构造函数1.1 -> 构造函数体赋值1.2 -> 初始化列表1.3 -> explicit关键字 2 -> static成员2.1 -> 概念2.2 -> 特性 3 -> 友元3.1 -> 友元函数3.2 -> 友元类 4 -> 内部类5 -> 匿名对象6 -> 拷贝对象时的一些编译器优化 1 -…...

解决TSP旅行商问题3个可以用Python编程的优化路径算法
旅行商问题(Traveling Salesman Problem, TSP)是一个经典的组合优化问题,它要求找到访问一系列城市并返回起点的最短可能路线,同时每个城市仅访问一次。这个问题是NP-hard的,意味着没有已知的多项式时间复杂度的精确算…...

10英寸安卓车载平板电脑丨ONERugged车载工业平板:解决农业工作效率
农业是人类社会的基石之一,而农业工作效率的提升一直是农民和农业专业人士关注的重要议题。随着技术的不断进步,车载工业平板成为了解决农业工作效率的创新解决方案。本文将探讨车载工业平板如何为农业带来巨大的改变,提高农民的工作效率和农…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...
