矩阵的正定(positive definite)性质的作用
1. 定义

注意,本文中正定和半正定矩阵不要求是对称或Hermite的。
2. 性质

3. 作用
(1)Ax=b直接法求解
| cholesky | 实对称正定矩阵求解 |
| 复共轭对称正定矩阵求解 | |
| LDL | 实对称非正定矩阵求解 |
| 复共轭对称非正定矩阵求解 | |
| 复对称矩阵求解 | |
| LU | 实非对称矩阵求解 |
| 复非对称矩阵求解 |
(2)特征值求解
在ARPACK(隐式重启Arnoldi算法)中,对K*x=lambda*M*x该广义特征值问题
M必须得是
| Mode | Operator | M |
| Shift | OP = inv[M]*K, and B = M. | 对称-正定 或Hemitian-正定 |
| Shift-and-invert | OP = (inv[K - sigma*M])*M, and B = M. | 对称-半正定 或Hemitian-半正定 |
注释:
- OP:operator,表示Arnoldi过程中与向量作用的算子,用户需要提供矩阵向量乘积w ← OPv
- M-inner product: <x,y> =
。
- M-orthogonal: x, y称为M-orthogonal若<x,y> = 0
- B: 用来定义M-inner product中的矩阵,用户需要提供矩阵向量乘积w ← Mv
Slepc有提及,若M不是正定也不是半正定的话,可以用EPS_GHIEP求解。
特征值中,正定或半正定性质对于 M 矩阵来说是一个优良属性,因为它确保了问题的物理可解性和数值计算的稳定性。例如,在结构动力学中,M 作为质量矩阵时,其正定性意味着系统的质量分布是非负的,这是物理上合理的。正定或半正定的 M 矩阵也有助于保证广义特征值问题解的良好性质,如确保所有特征值是实数且特征向量是良定义的。
然而,在某些情况下,M 矩阵可能不是正定或半正定的,这并不意味着广义特征值问题就无法求解。这些情况下,问题可能更加复杂,需要特别的数值方法来处理可能出现的数值不稳定性或解的不确定性。
相关文章:
矩阵的正定(positive definite)性质的作用
1. 定义 注意,本文中正定和半正定矩阵不要求是对称或Hermite的。 2. 性质 3. 作用 (1)Axb直接法求解 cholesky实对称正定矩阵求解复共轭对称正定矩阵求解LDL实对称非正定矩阵求解复共轭对称非正定矩阵求解复对称矩阵求解LU实非对称矩阵求解…...
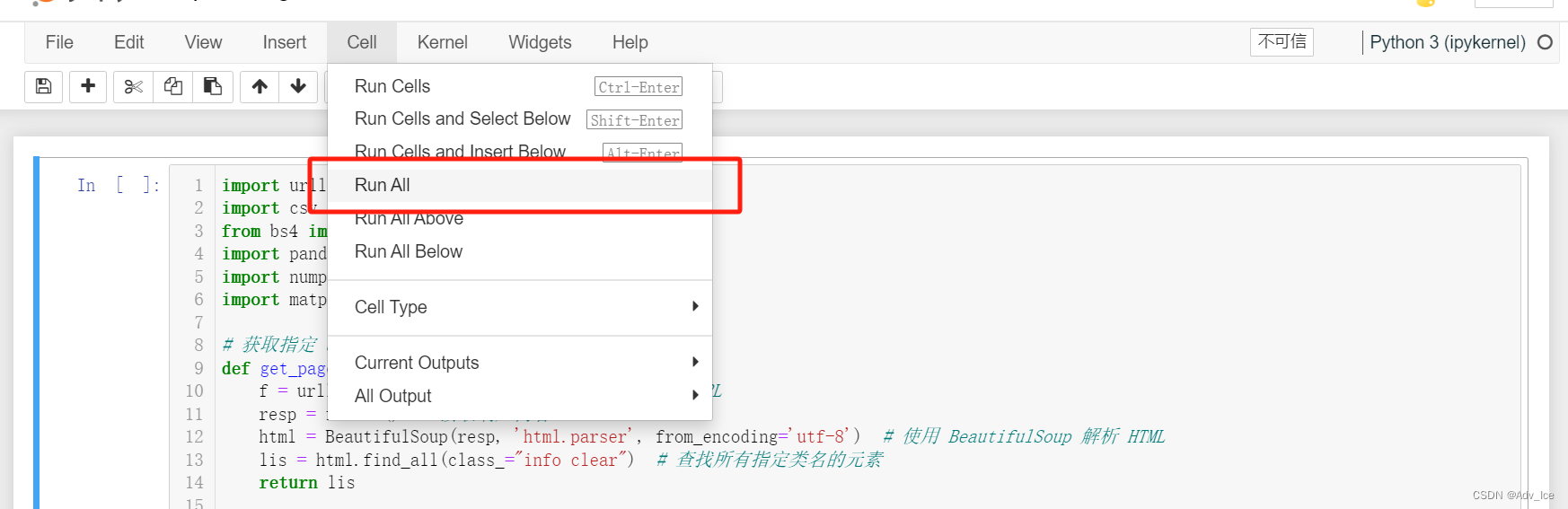
用python编写爬虫,爬取房产信息
题目 报告要求 工程报告链接放在这里 https://download.csdn.net/download/Samature/88816284使用 1.安装jupyter notebook 2.用jupyter notebook打开工程里的ipynb文件,再run all就行 注意事项 可能遇到的bug 暂无,有的话私信我...
Swift Combine 从入门到精通一
1. Combine 简介 用 Apple 官方的话来说,Combine 是: a declarative Swift API for processing values over time. Combine 是 Apple 用来实现函数响应式编程的库, 类似于 RxSwift。 RxSwift 是 ReactiveX 对 Swift 语言的实现。 Combine 使用了许多可以…...
探索前端开发框架:React、Angular 和 Vue 的对决(一)
🤍 前端开发工程师、技术日更博主、已过CET6 🍨 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 🕠 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 🍚 蓝桥云课签约作者、上架课程《Vue.js 和 E…...

企业飞书应用机器人,使用python发送图文信息到群
企业飞书应用的自动化,需要创建企业应用,应用开通机器人能力,并获取机器人所需的app_id与app_secret(这一部分大家可以在飞书的控制台获取:https://open.feishu.cn/api-explorer/) 文章目录 步骤1ÿ…...

设计模式1-访问者模式
访问者模式是一种行为设计模式,它允许你定义在对象结构中的元素上进行操作的新操作,而无需修改这些元素的类。这种模式的主要思想是将算法与元素的结构分离开,使得可以在不修改元素结构的情况下定义新的操作。 所谓算法与元素结构分离&#x…...

Android meminfo 查看方法及解析
目录 Android 上查看memory 信息的方法 内存限制的信息 手动释放缓存 例 adb shell dumpsys meminfo pid 解析 adb shell dumpsys meminfo 汇总信息说明 Total RAM Free RAM ION Used RAM Lost RAM ZRAM /proc/meminfo 参考文档 Android 上查看memory 信息的方法 …...

微信小程序解决华为手机保存图片到相册失败
1.新增隐私设置 2.优化代码 新增uni.authorize判断 _saveCode() {let that this;console.log(点击了保存图片)console.log(this.result)uni.authorize({scope: scope.writePhotosAlbum,success(e) {console.log(e)if (this.result ! "") {uni.saveImageToPhotosAlb…...
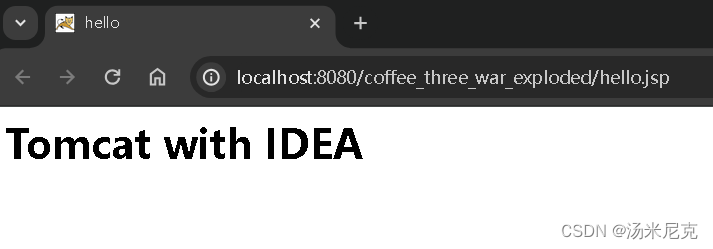
板块零 IDEA编译器基础:第三节 下载和在IDEA中集成 Tomcat服务器 来自【汤米尼克的JAVAEE全套教程专栏】
板块零 IDEA编译器基础:第三节 下载和在IDEA中集成 Tomcat服务器 一、为什么选择Tomcat(1)常见的JAVA WEB服务器(2)选择Tomcat的理由 二、Tomcat 8.5下载解压三、Tomcat 结构目录四、在IDEA中集成Tomcat 假设我们已经…...

2024/2/6
一、填空题 1、一个类的头文件如下所示,num初始化值为5,程序产生对象T,且修改num为10,并使用show()函数输出num的值10。 #include <iostream.h> class Test { private: static int num; public: Test(int); void sho…...

mysql清空表数据后如何让自增ID仍从1开始
有2种方法: 1、清空表时使用truncate命令,而不用delete命令 truncate test; 使用truncate命令的好处: 1)、速度快 2)、可以对自增ID进行重排,使自增ID仍从1开始计算 2、清空表数据后,使用alter…...
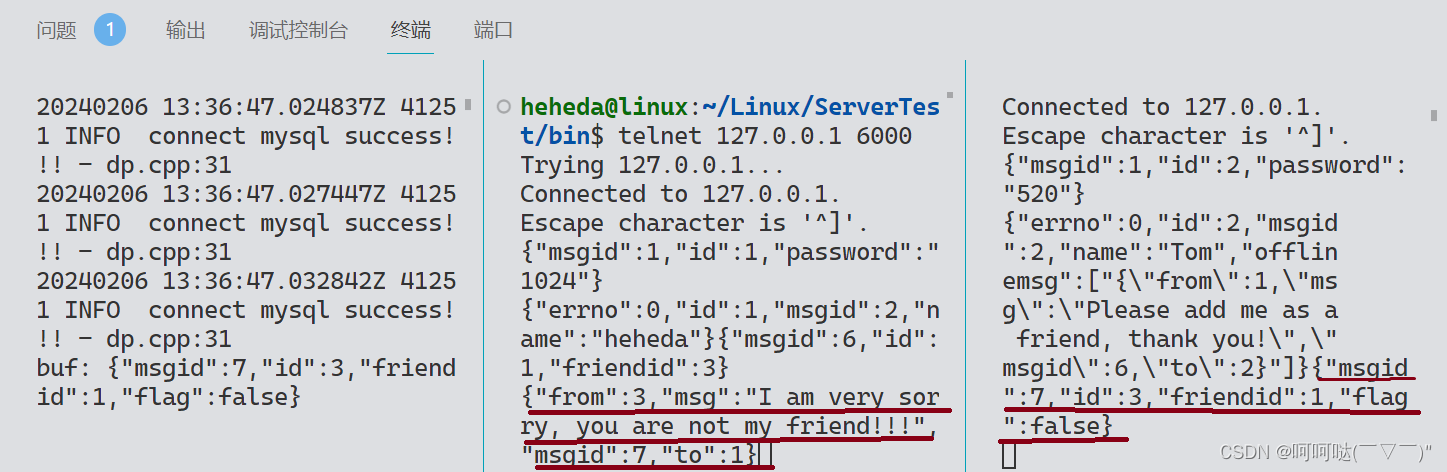
C++集群聊天服务器 数据模块+业务模块+CMake构建项目 笔记 (上)
跟着施磊老师做C项目,施磊老师_腾讯课堂 (qq.com) 本文在此篇博客的基础上继续实现数据模块和业务模块代码: C集群聊天服务器 网络模块业务模块CMake构建项目 笔记 (上)-CSDN博客https://blog.csdn.net/weixin_41987016/article…...

#Js篇:字符串的使用方法es5和es6
字符串 \ :单引号(\u0027)\" :双引号(\u0022) charAt 定义: 返回指定位置的字符,参数时从0开始编号的位置 参数: 位置下标 abc.charAt(1) // "b" …...
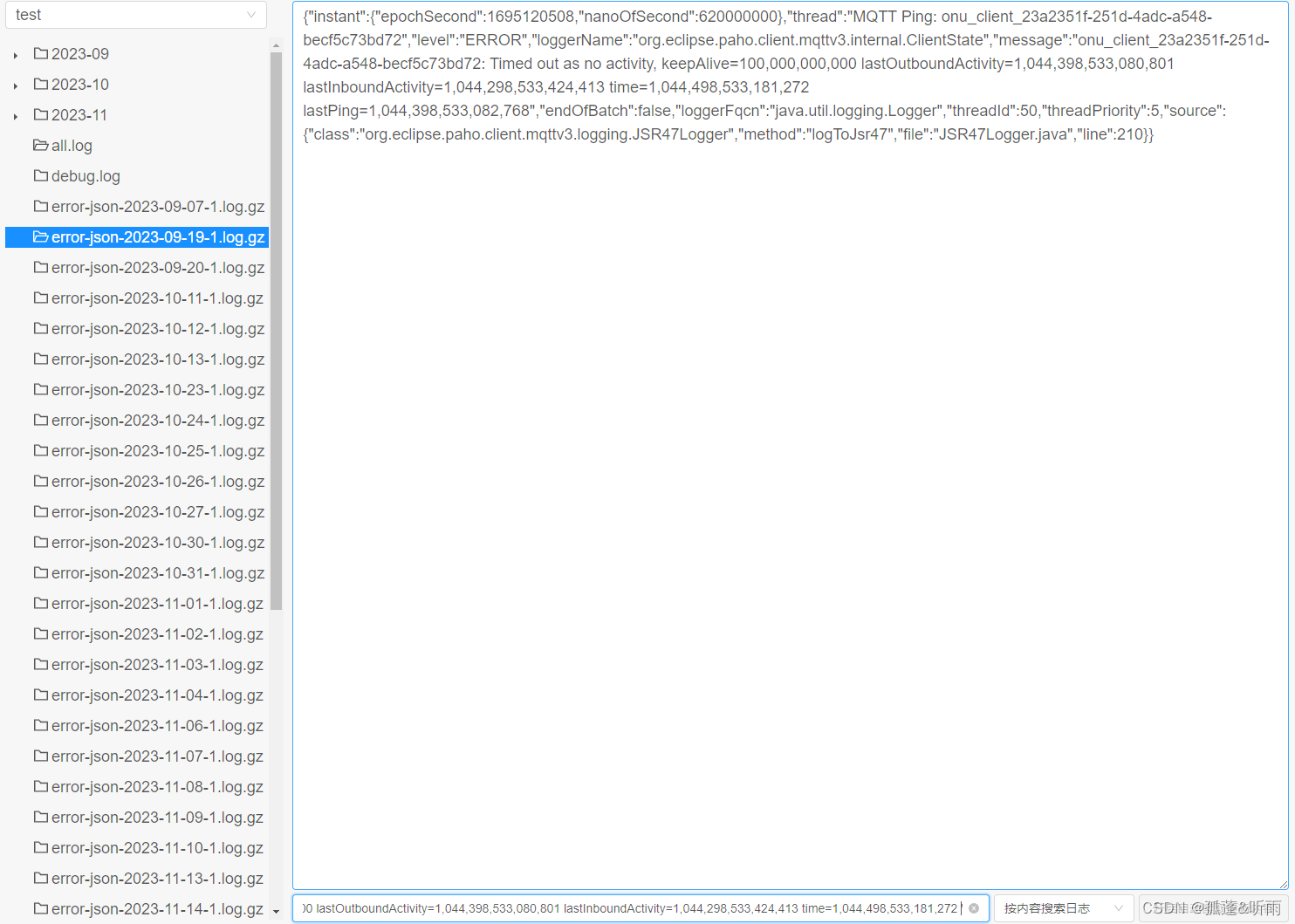
SpringBoo+Vue构建简洁日志文件查看系统
点击下载《SpringBooVue构建日志文件查看系统(源代码)》 1. 前言 想必经常做java开发的小伙伴,其大多数服务都是运行在linux系统上的,当遇到一些比较棘手的bug需要处理时,经常要上服务器去捞日志,然后通过…...
JavaScript基础第二天
JavaScript基础第二天 今天我们学习if分支语句、三元表达式和switch-case语句。 1. if分支语句 1.1 语法 if (条件表达式){// 满足条件要执行的语句 } else {// 不满足条件要执行的语句 }if中的内容如果为true,就执行大括号的代码块,如果为false执行…...

2、卷积和ReLU激活函数
python了解集合网络如何创建具有卷积层的特性。 文章目录 简介特征提取(Feature Extraction)卷积过滤(Filter with Convolution)Weights(权重)激活(Activations)用ReLU检测示例 - 应用卷积和ReLU结论In [1]: import numpy as np from itertools import productdef show_kerne…...

SQL世界之基础命令语句
目录 一、SQL SELECT 语句 1.SQL SELECT 语法 2.SQL SELECT 实例 3.SQL SELECT * 实例 二、SQL SELECT DISTINCT 语句 1.语法 2.使用 DISTINCT 关键词 三、SQL SELECT WHERE 语句 1.WHERE 子句 2.语法 3.使用 WHERE 子句 4.引号的使用 四、SQL SELECT AND&OR …...

Facebook未来展望:社交媒体的下一个篇章
社交媒体一直是连接人与人之间的纽带,而Facebook则一直在推动这一领域的发展。随着科技不断演进和社会需求的不断变迁,Facebook正积极筹谋社交媒体的下一个篇章。本文将深入剖析Facebook的未来展望,探讨其在社交媒体领域所迎接的新时代。 1. …...

源码搭建教学:直播带货商城小程序开发
结合小程序开发的直播带货商城,不仅可以提供更便捷的购物体验,还可以实现更高效的销售。因此,学习如何搭建一个直播带货商城小程序将成为您拓展商业领域的利器。 步骤一:准备工作 在开始开发之前,您需要进行一些准备工…...

vue-cli引入本地json数据:封装为js文件,无需请求直接读取
vue-cli引入本地json数据 1、新建js文件(路径自定义),写入JSON数据 /* jsonData.js */export let jsonData { // 声明变量,存储数据// JSON源数据 }2、组件内引入js文件,读取数据 /* Example.vue */import { json…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...
