【射影几何13 】梅氏定理和塞瓦定理探讨
梅氏定理和塞瓦定理
目录
- 一、说明
- 二、梅涅劳斯(Menelaus)定理
- 三、塞瓦(Giovanni Ceva)定理
- 四、塞瓦点的推广
一、说明
在射影几何中,梅涅劳斯(Menelaus)定理和塞瓦定理是非常重要的基本定理。通过这两个定理,可以导出多项结论,如:极点-极线性质、德萨格定理、pascal定理等;本篇专门叙述这两个定理证明。及相关启发。
二、梅涅劳斯(Menelaus)定理
梅涅劳斯(Menelaus)定理(简称梅氏定理)最早出现在由古希腊数学家梅涅劳斯的著作《球面学》(Sphaerica)中。
定理定义
当一条直线交 Δ A B C \Delta ABC ΔABC三边所在的直线 B C , A C , A B BC,AC,AB BC,AC,AB分别于点 D , E , F D,E,F D,E,F时,则有
A F F B B D D C C E E A = 1 \frac{AF}{FB} \frac{BD}{DC}\frac{CE}{EA}=1 FBAFDCBDEACE=1
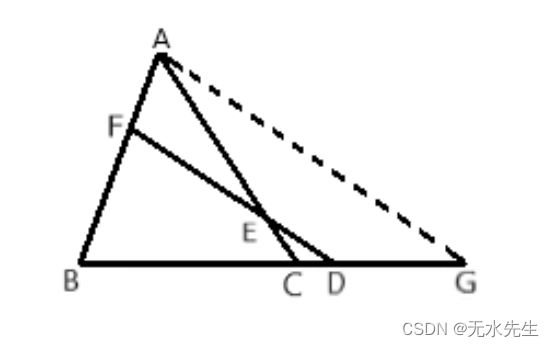
分析:显然, D , E , F D,E,F D,E,F分别为线段 B C , A C , A B BC,AC,AB BC,AC,AB的定比分点。因此:
A F F B = λ 1 ; B D D C = λ 2 ; C E E A = λ 3 \frac{AF}{FB}=\lambda_1 ; \; \frac{BD}{DC} =\lambda_2;\frac{CE}{EA}=\lambda_3 FBAF=λ1;DCBD=λ2;EACE=λ3
因此,等价说法是:
λ 1 λ 2 λ 3 = 1 \lambda_1 \lambda_2\lambda_3=1 λ1λ2λ3=1
[定理证明]
过点A作 A G ∥ D B AG\parallel DB AG∥DB交 B C BC BC的延长线于G点, 则:
A F F B = λ 1 = D G B D \frac{AF}{FB}=\lambda_1=\frac{DG}{BD} FBAF=λ1=BDDG
C E E A = λ 3 = C D D G \frac{CE}{EA}=\lambda_3=\frac{CD}{DG} EACE=λ3=DGCD
∴ A F F B B D D C C E E A = λ 1 λ 2 λ 3 = D G B D B D D C C D D G = 1 \therefore \frac{AF}{FB} \frac{BD}{DC}\frac{CE}{EA}= \lambda_1 \lambda_2\lambda_3=\frac{DG}{BD} \frac{BD}{DC}\frac{CD}{DG}=1 ∴FBAFDCBDEACE=λ1λ2λ3=BDDGDCBDDGCD=1
[证毕]
三、塞瓦(Giovanni Ceva)定理
塞瓦(Giovanni Ceva,1648~1734)意大利水利工程师,数学家。塞瓦定理载于塞瓦于1678年发表的《直线论》一书,也有书中说塞瓦定理是塞瓦重大发现。
【定理说明】
塞瓦定理是指在△ABC内任取一点O,延长AO、BO、CO分别交对边于D、E、F,则 (BD/DC)×(CE/EA)×(AF/FB)=1。
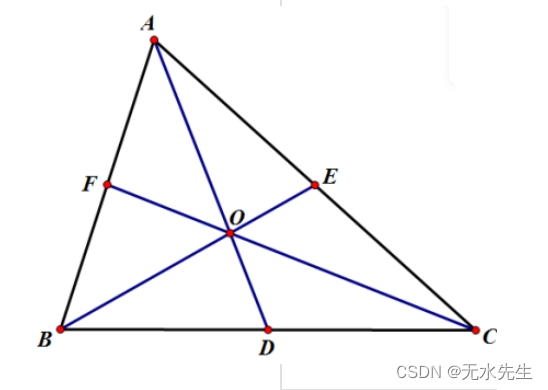
分析:

四、塞瓦点的推广
当塞瓦点在三角形外部,如下图:🔺ABC的三条线段的交点O位于三角形ABC的外部:
A F F B B D D C C E E A = 1 \frac{AF}{FB} \frac{BD}{DC}\frac{CE}{EA}=1 FBAFDCBDEACE=1
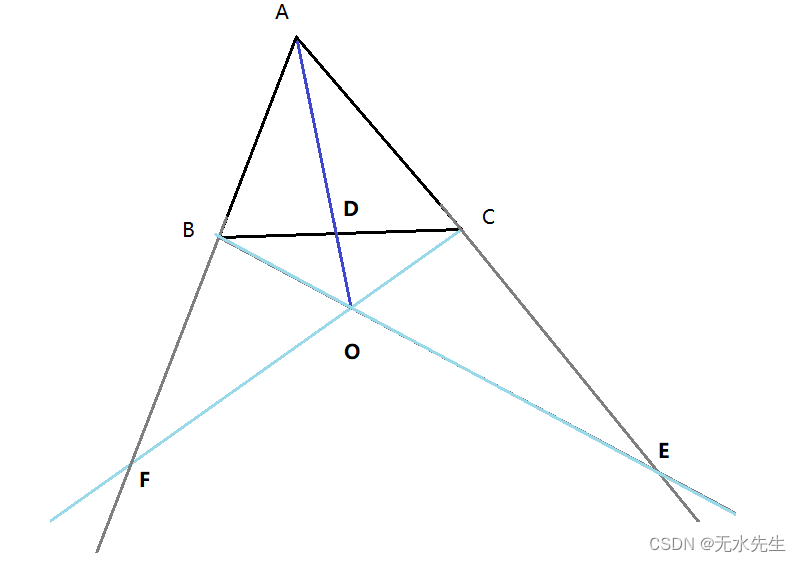
【证明】
B D D C = S Δ A B D S Δ A D C = S Δ O B D S Δ O D C \frac{BD}{DC} = \frac{S_{\Delta ABD}}{S_{\Delta ADC}} =\frac{S_{\Delta OBD}}{S_{\Delta ODC}} DCBD=SΔADCSΔABD=SΔODCSΔOBD
更比定理:
B D D C = S Δ A B D − S Δ O B D S Δ A D C − S Δ O B D = S Δ O B A S Δ C A O \frac{BD}{DC} = \frac{S_{\Delta ABD}-S_{\Delta OBD}}{S_{\Delta ADC}-S_{\Delta OBD}} =\frac{S_{\Delta OBA}}{S_{\Delta CAO}} DCBD=SΔADC−SΔOBDSΔABD−SΔOBD=SΔCAOSΔOBA
C E E A = S Δ B C O S Δ A B O \frac{CE}{EA} = \frac{S_{\Delta BCO}}{S_{\Delta ABO}} EACE=SΔABOSΔBCO
A F F B = S Δ C A O S Δ B C O \frac{AF}{FB} = \frac{S_{\Delta CAO}}{S_{\Delta BCO}} FBAF=SΔBCOSΔCAO
A F F B B D D C C E E A = S Δ C A O S Δ B C O S Δ O B A S Δ C A O S Δ B C O S Δ A B O = 1 \frac{AF}{FB} \frac{BD}{DC}\frac{CE}{EA}= \frac{S_{\Delta CAO}}{S_{\Delta BCO}}\frac{S_{\Delta OBA}}{S_{\Delta CAO}}\frac{S_{\Delta BCO}}{S_{\Delta ABO}} = 1 FBAFDCBDEACE=SΔBCOSΔCAOSΔCAOSΔOBASΔABOSΔBCO=1
【证毕】
相关文章:

【射影几何13 】梅氏定理和塞瓦定理探讨
梅氏定理和塞瓦定理 目录 一、说明二、梅涅劳斯(Menelaus)定理三、塞瓦(Giovanni Ceva)定理四、塞瓦点的推广 一、说明 在射影几何中,梅涅劳斯(Menelaus)定理和塞瓦定理是非常重要的基本定理。通过这两个定…...

Powershell Install 一键部署Openssl+certificate证书创建
前言 Openssl 是一个方便的实用程序,用于创建自签名证书。您可以在所有操作系统(如 Windows、MAC 和 Linux 版本)上使用 OpenSSL。 Windows openssl 下载 前提条件 开启wmi,配置网卡,参考 自签名证书 创建我们自己的根 CA 证书和 CA 私钥(我们自己充当 CA)创建服务器…...

SERVLET线程模型
1. SERVLET线程模型 Servlet规范定义了两种线程模型来阐明Web容器应该如何在多线程环境中处理servlet。第一种模型称为多线程模型,默认在此模型内执行所有servlet。在此模型中,每次客户机向servlet发送请求时Web容器都启动一个新线程。这意味着可能有多个线程同时访问servle…...

【开源】基于JAVA+Vue+SpringBoot的新能源电池回收系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 用户档案模块2.2 电池品类模块2.3 回收机构模块2.4 电池订单模块2.5 客服咨询模块 三、系统设计3.1 用例设计3.2 业务流程设计3.3 E-R 图设计 四、系统展示五、核心代码5.1 增改电池类型5.2 查询电池品类5.3 查询电池回…...

【蓝桥杯冲冲冲】Prime Gift
【蓝桥杯冲冲冲】Prime Gift 蓝桥杯备赛 | 洛谷做题打卡day31 文章目录 蓝桥杯备赛 | 洛谷做题打卡day31Prime Gift题面翻译题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 样例 #2样例输入 #2样例输出 #2 提示题解代码我的一些话 Prime Gift 题面翻译 给你 n n n 个…...
【PyQt】06-.ui文件转.py文件
文章目录 前言方法一、基本脚本查看自己的uic安装目录 方法二、添加到扩展工具里面(失败了)方法二的成功步骤总结 前言 方法一、基本脚本 将Qt Designer(一种图形用户界面设计工具)生成的.ui文件转换为Python代码的脚本。 pytho…...

λ-矩阵知识点
原文:链接 λ-矩阵 若矩阵 A \mathbf{A} A 的元素为关于 λ λ λ 的多项式,则称 A \mathbf{A} A 为 λ λ λ-矩阵 (表示为 A ( λ ) \mathbf{A}(λ) A(λ)). λ λ λ-矩阵也存在秩、逆、初等变换、相抵的概念, 但是有一些不同. 定义. λ λ λ-矩阵的秩是…...
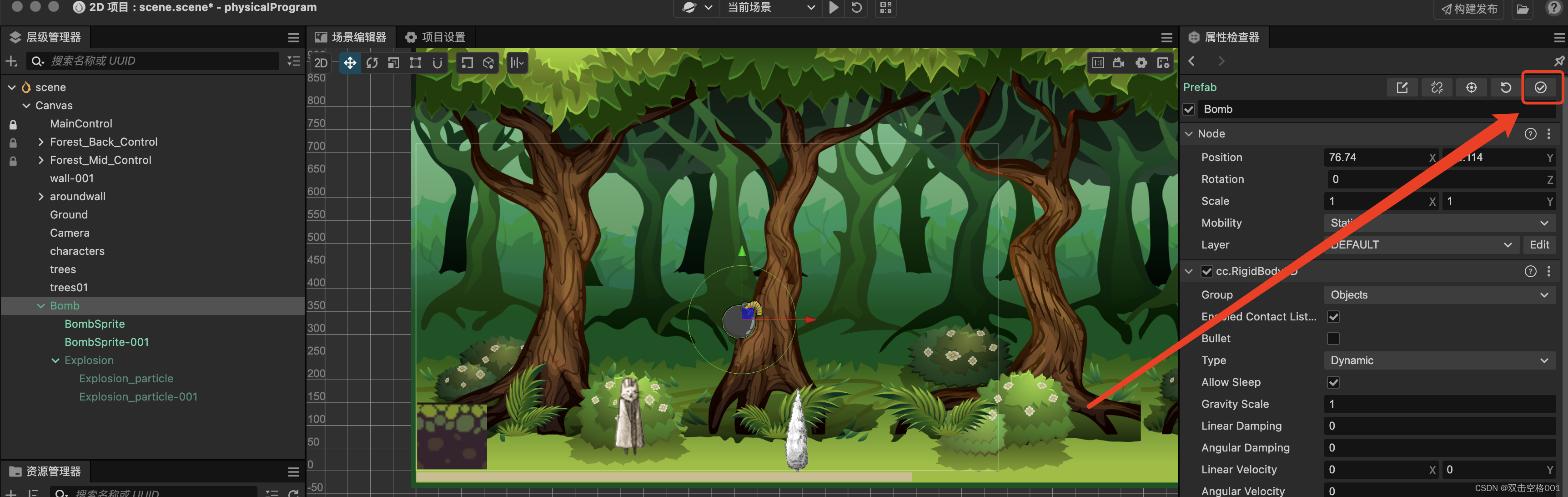
cocos creator 3.x 预制体无法显示
双击预制体,进入详情页,没有显示资源 Bomb 是个预制体,但是当我双击进来什么都没有了,无法对预制体进行可视化编辑 目前我只试出来一个解决方法: 把预制体拖进Canvas文件中,这样就能展示到屏幕上ÿ…...

Tomcat之虚拟主机
1.创建存放网页的目录 mkdir -p /web/{a,b} 2.添加jsp文件 vi /web/a/index.jsp <% page language"java" import"java.util.*" pageEncoding"UTF-8"%> <html> <head><title>JSP a page</title> </head> …...
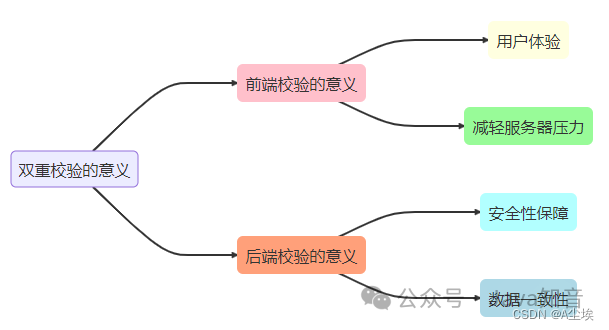
前后端数据校验
前端校验内容 前端开发中的必要校验,可以保证用户输入的数据的准确性、合法性和安全性。同时,这些校验也有助于提供良好的用户体验和防止不必要的错误提交到后端。 1、必填字段校验: 对于必填的字段,需确保用户输入了有效的数据…...

Python把png图片转成jpg图片
在Python中,您可以使用PIL(Python Imaging Library,也被称为Pillow)库来将PNG图片转换为JPG格式。以下是一个简单的示例: 首先,确保你已经安装了Pillow库。如果没有安装,可以使用pip来安装&…...
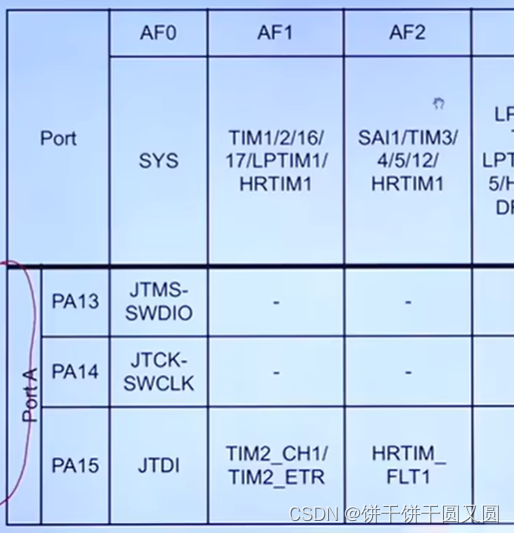
STM32搭建开发环境
常用开发工具简介 集成开发环境 MDK:全名RealViewMDK,是Keil公司(已被ARM收购的)一款集成开发环境,界面美观,简单易用,是STM32最常用的集成开发环境EWARM:IAR公司的一款集成开发环…...
C#入门详解_01_课程简介、C#语言简介、开发环境和学习资料的准备
文章目录 1. 课程简介2. C#语言简介3.开发环境与学习资料 1. 课程简介 开设本课程的目的 传播C#开发的知识,让更多的人有机会接触到软件开发行业引导有兴趣或者想转行的朋友进入软件开发行业 课程内容 完整讲述C#语言在实际软件开发中的应用采用知识讲述加实例程序…...
:确定服务器框架)
C++服务器端开发(2):确定服务器框架
选择C服务器框架时,可以考虑: 并发性能:C的强项之一是其并发性能。选择一个具有高并发处理能力的服务器框架,可以更好地满足大量并发请求的需求。例如,libevent、Boost.Asio和CppServer都是具有良好并发性能的C服务器框…...

CGAL::2D Arrangements-5
5.Arrangement无界曲线 前几章中构建和操作的所有Arrangement都只由线段引起,线段尤其是有界曲线。这样的Arrangement总是具有一个包含所有其他Arrangement特征的unbounded face。在本节中,我们将解释如何构造无界曲线的Arrangement。为了简化说明&…...
登录+JS逆向进阶【过咪咕登录】(附带源码)
JS渗透之咪咕登录 每篇前言:咪咕登录参数对比 captcha参数enpassword参数搜索enpassword参数搜索J_RsaPsd参数setPublic函数encrypt加密函数运行时可能会遇到的问题此部分改写的最终形态JS代码:运行结果python编写脚本运行此JS代码:运行结果&…...

CTF秀 ctfshow WEB入门 web1-10 wp精讲
目录 web1_查看源码 web3_抓包 web4-9_目录文件 web10_cookie web1_查看源码 ctrlu 查看源码 web3_抓包 查看源码,无果 抓包,找到flag web4-9_目录文件 GitHub - maurosoria/dirsearch: Web path scanner 下载dirsearch工具扫一下就都出来了 web4-…...
centos安装inpanel
前置条件 安装python yum -y install python 安装 cd /usr/local git clone https://gitee.com/WangZhe168_admin/inpanel.git cd inpanel python install.py 安装过程需要设置账户 密码 端口号 我设置的是admin:admin 10050 使用 打开浏览器,输入 http://192.168.168.…...

聊聊PowerJob Worker的ServerAddress
序 本文主要研究一下PowerJob Worker的ServerAddress PowerJobAutoConfiguration tech/powerjob/worker/autoconfigure/PowerJobAutoConfiguration.java BeanConditionalOnMissingBeanpublic PowerJobSpringWorker initPowerJob(PowerJobProperties properties) {PowerJobPr…...

师傅带练|大数据人工智能在线实习项目特色
大数据人工智能八大在线实习项目: 某实习网站招聘信息采集与分析 股票价格形态聚类与收益分析 某平台网络入侵用户自动识别 某平台广东省区采购数据分析 产品订单的数据分析与需求预测 基于注意力机制的评论者满意度分析 基于锅炉工况实现…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

【题解-洛谷】P10480 可达性统计
题目:P10480 可达性统计 题目描述 给定一张 N N N 个点 M M M 条边的有向无环图,分别统计从每个点出发能够到达的点的数量。 输入格式 第一行两个整数 N , M N,M N,M,接下来 M M M 行每行两个整数 x , y x,y x,y,表示从 …...
