λ-矩阵知识点
原文:链接
λ-矩阵
若矩阵 A \mathbf{A} A 的元素为关于 λ λ λ 的多项式,则称 A \mathbf{A} A 为 λ λ λ-矩阵 (表示为 A ( λ ) \mathbf{A}(λ) A(λ)).
λ λ λ-矩阵也存在秩、逆、初等变换、相抵的概念, 但是有一些不同.
定义. λ λ λ-矩阵的秩是指最高阶非零子式的阶数. 秩等于矩阵阶数则称矩阵是满秩的.
定理. λ λ λ-矩阵满秩等价于行列式不为 0 0 0.
定义. λ λ λ-矩阵的初等行变换有3种: ① 交换两行; ② 数乘行; ③ 一行乘以 ψ ( λ ) \psi(\lambda) ψ(λ) 倍加到另一行,其中 ψ ( λ ) \psi(\lambda) ψ(λ) 是以 λ \lambda λ 为变元的多项式. 类似地定义初等列变换. 初等行变换和初等列变换统称为初等变换.
可以看出, 初等行/列变换仅③和常数矩阵不同, 乘以常数换成了乘以多项式.
定义. 若一个 λ λ λ-矩阵可经有限次初等变换得到另一个 λ λ λ-矩阵, 则称两个矩阵相抵.
仿照常数矩阵, 可得如下定理:
定理. 相抵的 λ λ λ-矩阵一定等秩.
但等秩的矩阵不一定相抵.
借助Smith标准形的知识可以得如下定理:
定理. λ λ λ-矩阵相抵的充要条件是行列式差一个非零常系数.
定义. 对于 A ( λ ) \bm A(\lambda) A(λ), 若存在 λ λ λ-矩阵 B ( λ ) \bm B(\lambda) B(λ) 使得 A ( λ ) B ( λ ) = B ( λ ) A ( λ ) = I \bm A(\lambda) \bm B(\lambda)=\bm B(\lambda)\bm A(\lambda)=\bm I A(λ)B(λ)=B(λ)A(λ)=I, 则称 A ( λ ) \bm A(\lambda) A(λ) 为可逆阵, B ( λ ) \bm B(\lambda) B(λ) 为 A ( λ ) \bm A(\lambda) A(λ) 的逆矩阵.
λ λ λ-矩阵可逆一定满秩,但满秩不一定可逆.
仿照常数矩阵, 可得如下定理:
定理. λ λ λ-矩阵可逆的充要条件是行列式为非零常数.
定理. 对于 n n n 阶 λ λ λ-矩阵 A ( λ ) \bm A(\lambda) A(λ), 若存在 n n n 阶 λ λ λ-矩阵 B ( λ ) \bm B(\lambda) B(λ), 满足 A ( λ ) B ( λ ) = I \bm A(\lambda) \bm B(\lambda)=\bm{I} A(λ)B(λ)=I/ B ( λ ) A ( λ ) = I \bm B(\lambda) \bm A(\lambda)=\bm{I} B(λ)A(λ)=I, 则 A ( λ ) \bm A(\lambda) A(λ) 是可逆的, 其逆矩阵为 B ( λ ) \bm B(\lambda) B(λ).
借助Smith标准形的知识可以得如下定理:
定理. λ λ λ-矩阵可逆的充要条件是相抵于单位阵.
相关文章:

λ-矩阵知识点
原文:链接 λ-矩阵 若矩阵 A \mathbf{A} A 的元素为关于 λ λ λ 的多项式,则称 A \mathbf{A} A 为 λ λ λ-矩阵 (表示为 A ( λ ) \mathbf{A}(λ) A(λ)). λ λ λ-矩阵也存在秩、逆、初等变换、相抵的概念, 但是有一些不同. 定义. λ λ λ-矩阵的秩是…...
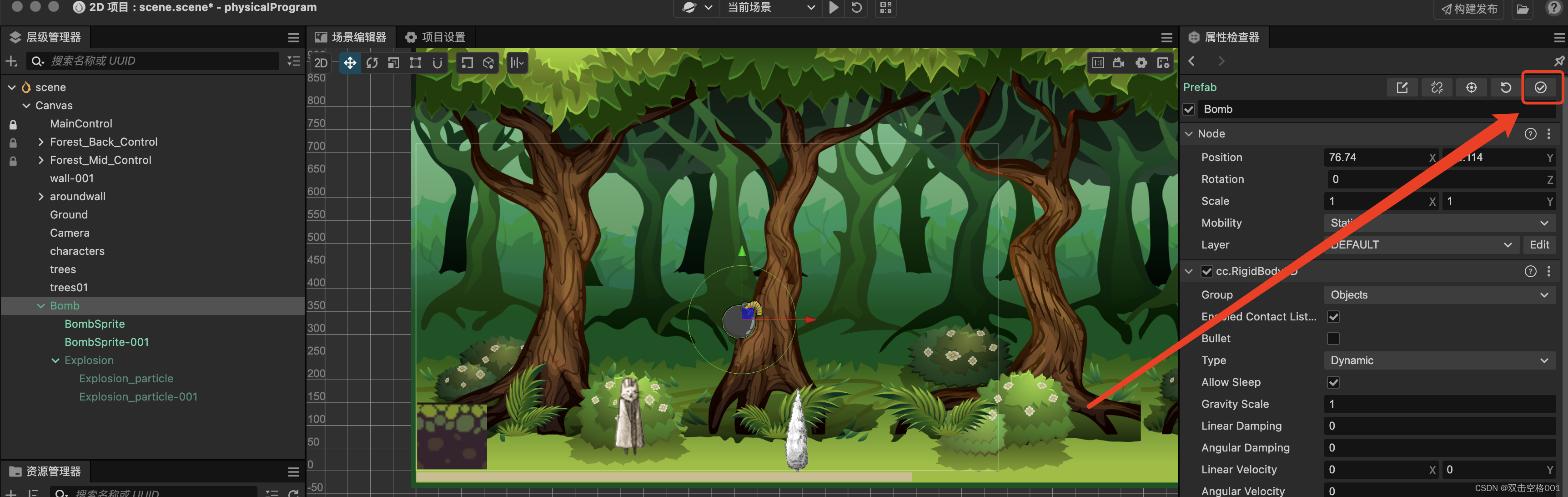
cocos creator 3.x 预制体无法显示
双击预制体,进入详情页,没有显示资源 Bomb 是个预制体,但是当我双击进来什么都没有了,无法对预制体进行可视化编辑 目前我只试出来一个解决方法: 把预制体拖进Canvas文件中,这样就能展示到屏幕上ÿ…...

Tomcat之虚拟主机
1.创建存放网页的目录 mkdir -p /web/{a,b} 2.添加jsp文件 vi /web/a/index.jsp <% page language"java" import"java.util.*" pageEncoding"UTF-8"%> <html> <head><title>JSP a page</title> </head> …...
前后端数据校验
前端校验内容 前端开发中的必要校验,可以保证用户输入的数据的准确性、合法性和安全性。同时,这些校验也有助于提供良好的用户体验和防止不必要的错误提交到后端。 1、必填字段校验: 对于必填的字段,需确保用户输入了有效的数据…...

Python把png图片转成jpg图片
在Python中,您可以使用PIL(Python Imaging Library,也被称为Pillow)库来将PNG图片转换为JPG格式。以下是一个简单的示例: 首先,确保你已经安装了Pillow库。如果没有安装,可以使用pip来安装&…...
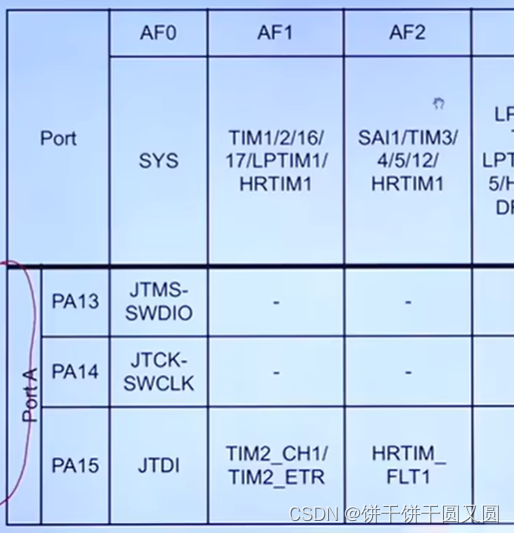
STM32搭建开发环境
常用开发工具简介 集成开发环境 MDK:全名RealViewMDK,是Keil公司(已被ARM收购的)一款集成开发环境,界面美观,简单易用,是STM32最常用的集成开发环境EWARM:IAR公司的一款集成开发环…...
C#入门详解_01_课程简介、C#语言简介、开发环境和学习资料的准备
文章目录 1. 课程简介2. C#语言简介3.开发环境与学习资料 1. 课程简介 开设本课程的目的 传播C#开发的知识,让更多的人有机会接触到软件开发行业引导有兴趣或者想转行的朋友进入软件开发行业 课程内容 完整讲述C#语言在实际软件开发中的应用采用知识讲述加实例程序…...
:确定服务器框架)
C++服务器端开发(2):确定服务器框架
选择C服务器框架时,可以考虑: 并发性能:C的强项之一是其并发性能。选择一个具有高并发处理能力的服务器框架,可以更好地满足大量并发请求的需求。例如,libevent、Boost.Asio和CppServer都是具有良好并发性能的C服务器框…...

CGAL::2D Arrangements-5
5.Arrangement无界曲线 前几章中构建和操作的所有Arrangement都只由线段引起,线段尤其是有界曲线。这样的Arrangement总是具有一个包含所有其他Arrangement特征的unbounded face。在本节中,我们将解释如何构造无界曲线的Arrangement。为了简化说明&…...
登录+JS逆向进阶【过咪咕登录】(附带源码)
JS渗透之咪咕登录 每篇前言:咪咕登录参数对比 captcha参数enpassword参数搜索enpassword参数搜索J_RsaPsd参数setPublic函数encrypt加密函数运行时可能会遇到的问题此部分改写的最终形态JS代码:运行结果python编写脚本运行此JS代码:运行结果&…...

CTF秀 ctfshow WEB入门 web1-10 wp精讲
目录 web1_查看源码 web3_抓包 web4-9_目录文件 web10_cookie web1_查看源码 ctrlu 查看源码 web3_抓包 查看源码,无果 抓包,找到flag web4-9_目录文件 GitHub - maurosoria/dirsearch: Web path scanner 下载dirsearch工具扫一下就都出来了 web4-…...
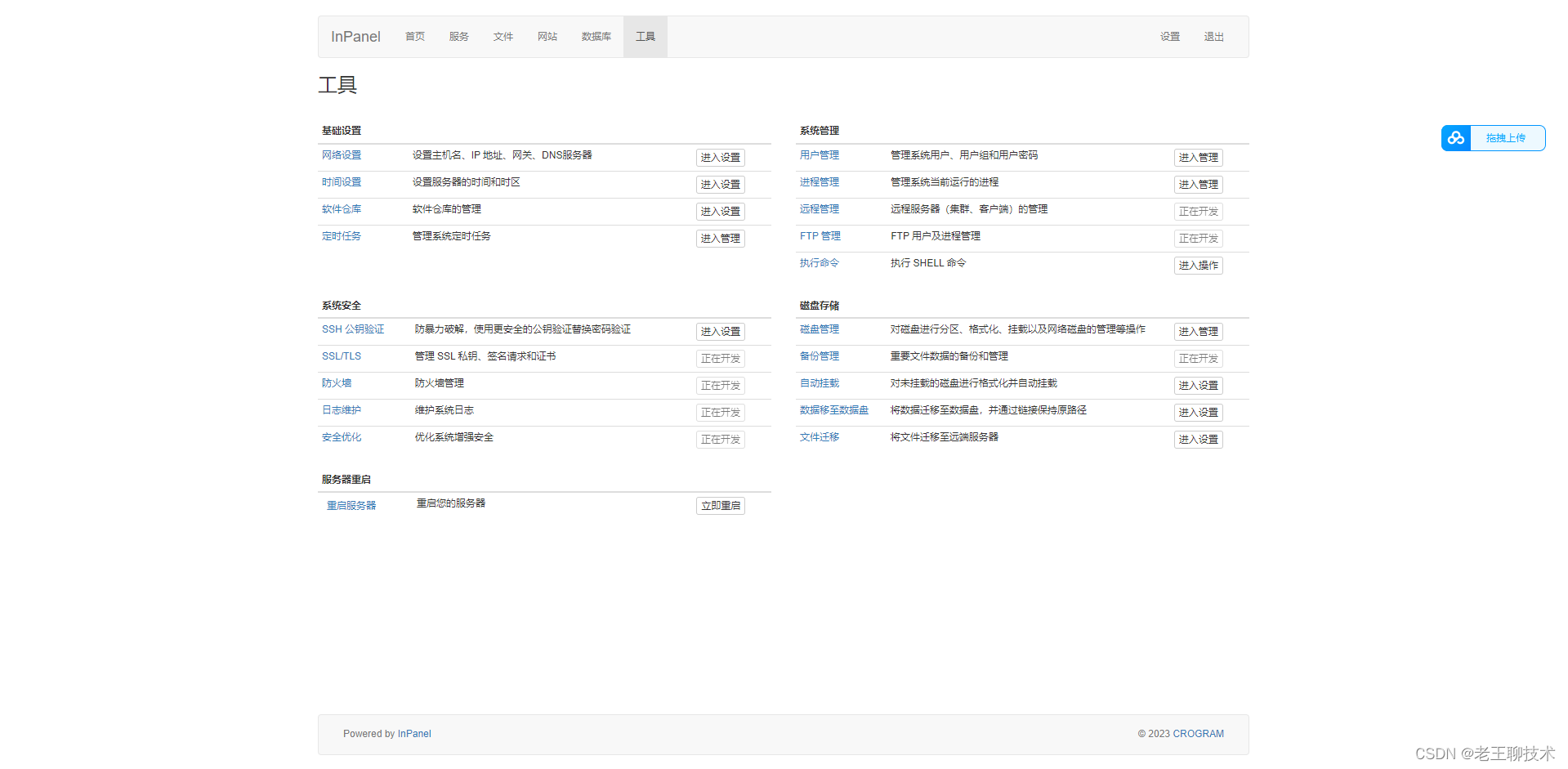
centos安装inpanel
前置条件 安装python yum -y install python 安装 cd /usr/local git clone https://gitee.com/WangZhe168_admin/inpanel.git cd inpanel python install.py 安装过程需要设置账户 密码 端口号 我设置的是admin:admin 10050 使用 打开浏览器,输入 http://192.168.168.…...

聊聊PowerJob Worker的ServerAddress
序 本文主要研究一下PowerJob Worker的ServerAddress PowerJobAutoConfiguration tech/powerjob/worker/autoconfigure/PowerJobAutoConfiguration.java BeanConditionalOnMissingBeanpublic PowerJobSpringWorker initPowerJob(PowerJobProperties properties) {PowerJobPr…...

师傅带练|大数据人工智能在线实习项目特色
大数据人工智能八大在线实习项目: 某实习网站招聘信息采集与分析 股票价格形态聚类与收益分析 某平台网络入侵用户自动识别 某平台广东省区采购数据分析 产品订单的数据分析与需求预测 基于注意力机制的评论者满意度分析 基于锅炉工况实现…...

ant-design-vue表格嵌套子表格,实现子表格有数据才显示左侧加号图标
ant-design-vue表格嵌套子表格,实现子表格有数据才显示左侧加号图标 通过使用插槽的方式,以下为全部项目的代码,关键的代码就两块,看注释 <template><a-card><a-form class"kit_form" ref"formRef…...
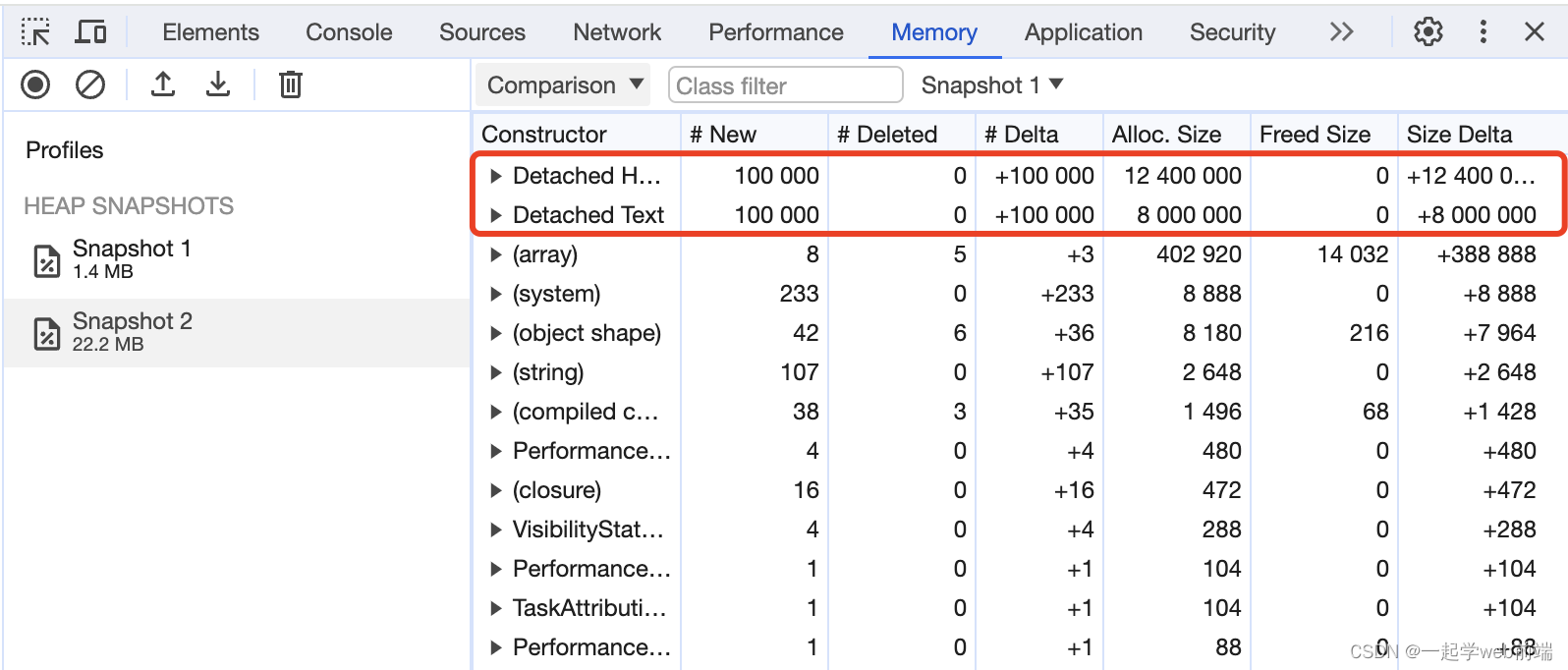
浅谈垃圾回收、内存泄漏与闭包
什么是垃圾? 在js中,垃圾通常指的是不再被程序使用的内存或对象。也就是说,垃圾是指程序中分配的内存空间或对象,但不再被程序使用或无法被访问到的内容 function createIncrease() {const doms new Array(100000).fill(0).map((…...

2 月 7 日算法练习- 数据结构-树状数组
树状数组 lowbit 在学习树状数组之前,我们需要了解lowbit操作,这是一种位运算操作,用于计算出数字的二进制表达中的最低位的1以及后面所有的0。 写法很简单: int lowbit(int x){return x &am…...

[AIGC] 开源流程引擎哪个好,如何选型?
开源流程引擎是指一种自动化的工作流解决方案,它可以帮助你管理和协调你的业务流程和决策。但是,在开源世界里,有许多不同的流程引擎可以选择。因此,如何选择适合你的开源流程引擎,是一个具有挑战性和价值的话题。 文章…...

服务器使用过程中遇到常见故障及解决方案(包括蓝屏死机、无法删除的文件如何清理、网络卡、服务器连接不上等)
互联网时代,服务器的安全性和稳定性尤为重要,支撑着整个互联网行业的信息和数据安全。最近经常有客户咨询服务器的日常故障排除方法。由于服务器复杂的硬件结构和繁琐的运行原理,经常会出现这样那样的问题,有时即使是最小的问题也…...

【推荐算法】userid是否需要建模
看到一个din的源码,将userid也构建了emb table。 于是调研了一下。即推荐算法需要建模userid吗? 深度学习推荐算法中user-id和item-id是否需要放入模型中作为特征进行训练呢? 深度学习推荐算法中user-id和item-id是否需要放入模型中作为特…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
