常用排序算法(Java版本)
1 引言
常见的排序算法有八种:交换排序【冒泡排序、快速排序】、插入排序【直接插入排序、希尔排序】、选择排序【简单选择排序、堆排序】、归并排序、基数排序。
2 交换排序
所谓交换,就是序列中任意两个元素进行比较,根据比较结果来交换各自在序列中的位置,以此达到排序的目的。
2.1 冒泡排序
冒泡排序是一种简单的交换排序算法,以升序排序为例,其核心思想是:
- 从第一个元素开始,比较相邻的两个元素。如果第一个比第二个大,则进行交换。
- 轮到下一组相邻元素,执行同样的比较操作,再找下一组,直到没有相邻元素可比较为止,此时最后的元素应是最大的数。
- 除了每次排序得到的最后一个元素,对剩余元素重复以上步骤,直到没有任何一对元素需要比较为止。
public void bubbleSortOpt(int[] nums) {if (nums == null) {return;}int temp;for (int i = 0; i < nums.length; i++) {for (int j = 0; j < nums.length - 1 - i; j++) {if (nums[j] > nums[j + 1]) {temp = nums[j];nums[j] = nums[j + 1];nums[j + 1] = temp;}}}}
2.2 快速排序
快速排序的思想很简单,就是先把待排序的数组拆成左右两个区间,左边都比中间的基准数小,右边都比基准数大。接着左右两边各自再做同样的操作,完成后再拆分再继续,一直到各区间只有一个数为止。
举个例子,现在我要排序 4、9、5、1、2、6 这个数组。一般取首位的 4 为基准数,第一次排序的结果是:
2、1、4、5、9、6
可能有人觉得奇怪,2 和 1 交换下位置也能满足条件,为什么 2 在首位?这其实由实际的代码实现来决定,并不影响之后的操作。以 4 为分界点,对 2、1、4 和 5、9、6 各自排序,得到:
1、2、4、5、9、6
不用管左边的 1、2、4 了,将 5、9、6 拆成 5 和 9、6,再排序,至此结果为:
1、2、4、5、6、9
为什么把快排划到交换排序的范畴呢?因为元素的移动也是靠交换位置来实现的。算法的实现需要用到递归(拆分区间之后再对每个区间作同样的操作)
public void quicksort(int[] arr, int start, int end) {if (start < end) {int stard = arr[start];int low = start;int high = end;while (low < high) {while (low < high && stard <= arr[high]) {high--;}arr[low] = arr[high];while (low < high && stard >= arr[low]) {low++;}arr[high] = arr[low];}arr[low] = stard;quicksort(arr, start, low);quicksort(arr, low + 1, end);}}
3 插入排序
插入排序是一种简单的排序方法,其基本思想是将一个记录插入到已经排好序的有序表中,使得被插入数的序列同样是有序的。按照此法对所有元素进行插入,直到整个序列排为有序的过程。
3.1 直接插入排序
直接插入排序就是插入排序的粗暴实现。对于一个序列,选定一个下标,认为在这个下标之前的元素都是有序的。将下标所在的元素插入到其之前的序列中。接着再选取这个下标的后一个元素,继续重复操作。直到最后一个元素完成插入为止。我们一般从序列的第二个元素开始操作。

public void insertSort(int[] nums) {// 遍历所有数字for (int i = 1; i < nums.length; i++) {if (nums[i] < nums[i - 1]) {// 把当前遍历的数字保存一下int temp = nums[i];int j;// 前一个数字按序移动到后一个数字上for (j = i - 1; j >= 0 && nums[j] >= temp; j--) {nums[j + 1] = nums[j];}nums[j + 1] = temp;}}}
3.2 希尔排序
某些情况下直接插入排序的效率极低。比如一个已经有序的升序数组,这时再插入一个比最小值还要小的数,也就意味着被插入的数要和数组所有元素比较一次。我们需要对直接插入排序进行改进。
怎么改进呢?前面提过,插入排序对已经排好序的数组操作时,效率很高。因此我们可以试着先将数组变为一个相对有序的数组,然后再做插入排序。
希尔排序能实现这个目的。希尔排序把序列按下标的一定增量(步长)分组,对每组分别使用插入排序。随着增量(步长)减少,一直到一,算法结束,整个序列变为有序。因此希尔排序又称缩小增量排序。
一般来说,初次取序列的一半为增量,以后每次减半,直到增量为一。

public void shellSort(int[] nums) {for (int gap = nums.length / 2; gap > 0; gap /= 2) {for (int i = 0; i < gap; i++) {for (int j = i + gap; j < nums.length; j += gap) {if (nums[j] < nums[j - gap]) {int k;int temp = nums[j];for (k = j - gap; k >= 0 && nums[k] > temp; k -= gap) {nums[k + gap] = nums[k];}nums[k + gap] = temp;}}}}}
4 选择排序
选择排序是一种简单直观的排序算法,首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
4.1 简单选择排序
选择排序思想的暴力实现,每一趟从未排序的区间找到一个最小元素,并放到第一位,直到全部区间有序为止。
public void selectSort(int[] nums) {for (int i = 0; i < nums.length; i++) {int minIndex = i;for (int j = i + 1; j < nums.length; j++) {if (nums[j] < nums[minIndex]) {minIndex = j;}}if (i != minIndex) {int temp = nums[i];nums[i] = nums[minIndex];nums[minIndex] = temp;}}}
4.2 堆排序
我们知道,对于任何一个数组都可以看成一颗完全二叉树。堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。如下图:

像上图的大顶堆,映射为数组,就是 [50, 45, 40, 20, 25, 35, 30, 10, 15]。可以发现第一个下标的元素就是最大值,将其与末尾元素交换,则末尾元素就是最大值。所以堆排序的思想可以归纳为以下两步:
根据初始数组构造堆
每次交换第一个和最后一个元素,然后将除最后一个元素以外的其他元素重新调整为大顶堆
重复以上两个步骤,直到没有元素可操作,就完成排序了。
我们需要把一个普通数组转换为大顶堆,调整的起始点是最后一个非叶子结点,然后从左至右,从下至上,继续调整其他非叶子结点,直到根结点为止。
/*** 转化为大顶堆* @param arr 待转化的数组* @param size 待调整的区间长度* @param index 结点下标*/
public void maxHeap(int[] arr, int size, int index) {// 左子结点int leftNode = 2 * index + 1;// 右子结点int rightNode = 2 * index + 2;int max = index;// 和两个子结点分别对比,找出最大的结点if (leftNode < size && arr[leftNode] > arr[max]) {max = leftNode;}if (rightNode < size && arr[rightNode] > arr[max]) {max = rightNode;}// 交换位置if (max != index) {int temp = arr[index];arr[index] = arr[max];arr[max] = temp;// 因为交换位置后有可能使子树不满足大顶堆条件,所以要对子树进行调整maxHeap(arr, size, max);}
}/*** 堆排序* @param arr 待排序的整型数组*/
public static void heapSort(int[] arr) {// 开始位置是最后一个非叶子结点,即最后一个结点的父结点int start = (arr.length - 1) / 2;// 调整为大顶堆for (int i = start; i >= 0; i--) {SortTools.maxHeap(arr, arr.length, i);}// 先把数组中第 0 个位置的数和堆中最后一个数交换位置,再把前面的处理为大顶堆for (int i = arr.length - 1; i > 0; i--) {int temp = arr[0];arr[0] = arr[i];arr[i] = temp;maxHeap(arr, i, 0);}
}
5 归并排序
归并排序是建立在归并操作上的一种有效,稳定的排序算法。该算法采用分治法的思想,是一个非常典型的应用。归并排序的思路如下:
- 将 n 个元素分成两个各含 n/2 个元素的子序列
- 借助递归,两个子序列分别继续进行第一步操作,直到不可再分为止
- 此时每一层递归都有两个子序列,再将其合并,作为一个有序的子序列返回上一层,再继续合并,全部完成之后得到的就是一个有序的序列
关键在于两个子序列应该如何合并。假设两个子序列各自都是有序的,那么合并步骤就是:
- 创建一个用于存放结果的临时数组,其长度是两个子序列合并后的长度
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置
- 比较两个指针所指向的元素,选择相对小的元素放入临时数组,并移动指针到下一位置
- 重复步骤 3 直到某一指针达到序列尾
- 将另一序列剩下的所有元素直接复制到合并序列尾
/*** 合并数组*/
public static void merge(int[] arr, int low, int middle, int high) {// 用于存储归并后的临时数组int[] temp = new int[high - low + 1];// 记录第一个数组中需要遍历的下标int i = low;// 记录第二个数组中需要遍历的下标int j = middle + 1;// 记录在临时数组中存放的下标int index = 0;// 遍历两个数组,取出小的数字,放入临时数组中while (i <= middle && j <= high) {// 第一个数组的数据更小if (arr[i] <= arr[j]) {// 把更小的数据放入临时数组中temp[index] = arr[i];// 下标向后移动一位i++;} else {temp[index] = arr[j];j++;}index++;}// 处理剩余未比较的数据while (i <= middle) {temp[index] = arr[i];i++;index++;}while (j <= high) {temp[index] = arr[j];j++;index++;}// 把临时数组中的数据重新放入原数组for (int k = 0; k < temp.length; k++) {arr[k + low] = temp[k];}
}/*** 归并排序*/
public static void mergeSort(int[] arr, int low, int high) {int middle = (high + low) / 2;if (low < high) {// 处理左边数组mergeSort(arr, low, middle);// 处理右边数组mergeSort(arr, middle + 1, high);// 归并merge(arr, low, middle, high);}
}
6 基数排序
基数排序的原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。为此需要将所有待比较的数值统一为同样的数位长度,数位不足的数在高位补零。
/*** 基数排序*/
public static void radixSort(int[] arr) {// 存放数组中的最大数字int max = Integer.MIN_VALUE;for (int value : arr) {if (value > max) {max = value;}}// 计算最大数字是几位数int maxLength = (max + "").length();// 用于临时存储数据int[][] temp = new int[10][arr.length];// 用于记录在 temp 中相应的下标存放数字的数量int[] counts = new int[10];// 根据最大长度的数决定比较次数for (int i = 0, n = 1; i < maxLength; i++, n *= 10) {// 每一个数字分别计算余数for (int j = 0; j < arr.length; j++) {// 计算余数int remainder = arr[j] / n % 10;// 把当前遍历的数据放到指定的数组中temp[remainder][counts[remainder]] = arr[j];// 记录数量counts[remainder]++;}// 记录取的元素需要放的位置int index = 0;// 把数字取出来for (int k = 0; k < counts.length; k++) {// 记录数量的数组中当前余数记录的数量不为 0if (counts[k] != 0) {// 循环取出元素for (int l = 0; l < counts[k]; l++) {arr[index] = temp[k][l];// 记录下一个位置index++;}// 把数量置空counts[k] = 0;}}}
}
7 算法性能
| 序号 | 排序算法 | 时间复杂度(平均) | 时间复杂度(最坏) | 时间复杂度(最好) | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|---|
| 1 | 冒泡排序 | O(n^2) | O(n^2) | O(n) | O(1) | 稳定 |
| 2 | 快速排序 | O(n log n) | O(n^2) | O(n log n) | O(n log n) | 不稳定 |
| 3 | 直接插入排序 | O(n^2) | O(n^2) | O(n) | O(1) | 稳定 |
| 4 | 希尔排序 | O(n log n) | O(n^2) | O(n) | O(1) | 不稳定 |
| 5 | 简单选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 |
| 6 | 堆排序 | O(n log n) | O(n log n) | O(n log n) | O(n log n) | 不稳定 |
| 7 | 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | 稳定 |
| 8 | 基数排序 | O(n*k) | O(n*k) | O(n*k) | O(n+k) | 稳定 |
返回面试宝典
相关文章:

常用排序算法(Java版本)
1 引言 常见的排序算法有八种:交换排序【冒泡排序、快速排序】、插入排序【直接插入排序、希尔排序】、选择排序【简单选择排序、堆排序】、归并排序、基数排序。 2 交换排序 所谓交换,就是序列中任意两个元素进行比较,根据比较结果来交换…...

CPP项目:Boost搜索引擎
1.项目背景 对于Boost库来说,它是没有搜索功能的,所以我们可以实现一个Boost搜索引擎来实现一个简单的搜索功能,可以更快速的实现Boost库的查找,在这里,我们实现的是站内搜索,而不是全网搜索。 2.对于搜索…...
)
【洛谷 P1616】疯狂的采药 题解(动态规划+完全背包)
疯狂的采药 题目背景 此题为纪念 LiYuxiang 而生。 题目描述 LiYuxiang 是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草…...

L1-027 出租分数 20
下面是新浪微博上曾经很火的一张图: 一时间网上一片求救声,急问这个怎么破。其实这段代码很简单,index数组就是arr数组的下标,index[0]2 对应 arr[2]1,index[1]0 对应 arr[0]8,index[2]3 对应 arr[3]0&…...

51单片机精进之路-1点亮led灯
本例中led灯使用共阳极连接在电路中,共阳极即将led的正极接在一起,通过上拉电阻接到电源正极,通过单片机io与Led的负极相连,io输出低电平,有电流从led流过,此时led点亮,当io输出高电平时&#x…...
嵌入式学习Day14 C语言 --- 位运算
位运算 注意:符号位也遵循这个规则 一、按位与(&) 运算规则:一假则假 int a 0x33;a & 0x55;0011 00110101 0101 &----------0001 0001 //0x11 二、按位或(|) 运算规则:一真则真 int a 0x33;a |0x55;0011 00110101 0101 |…...
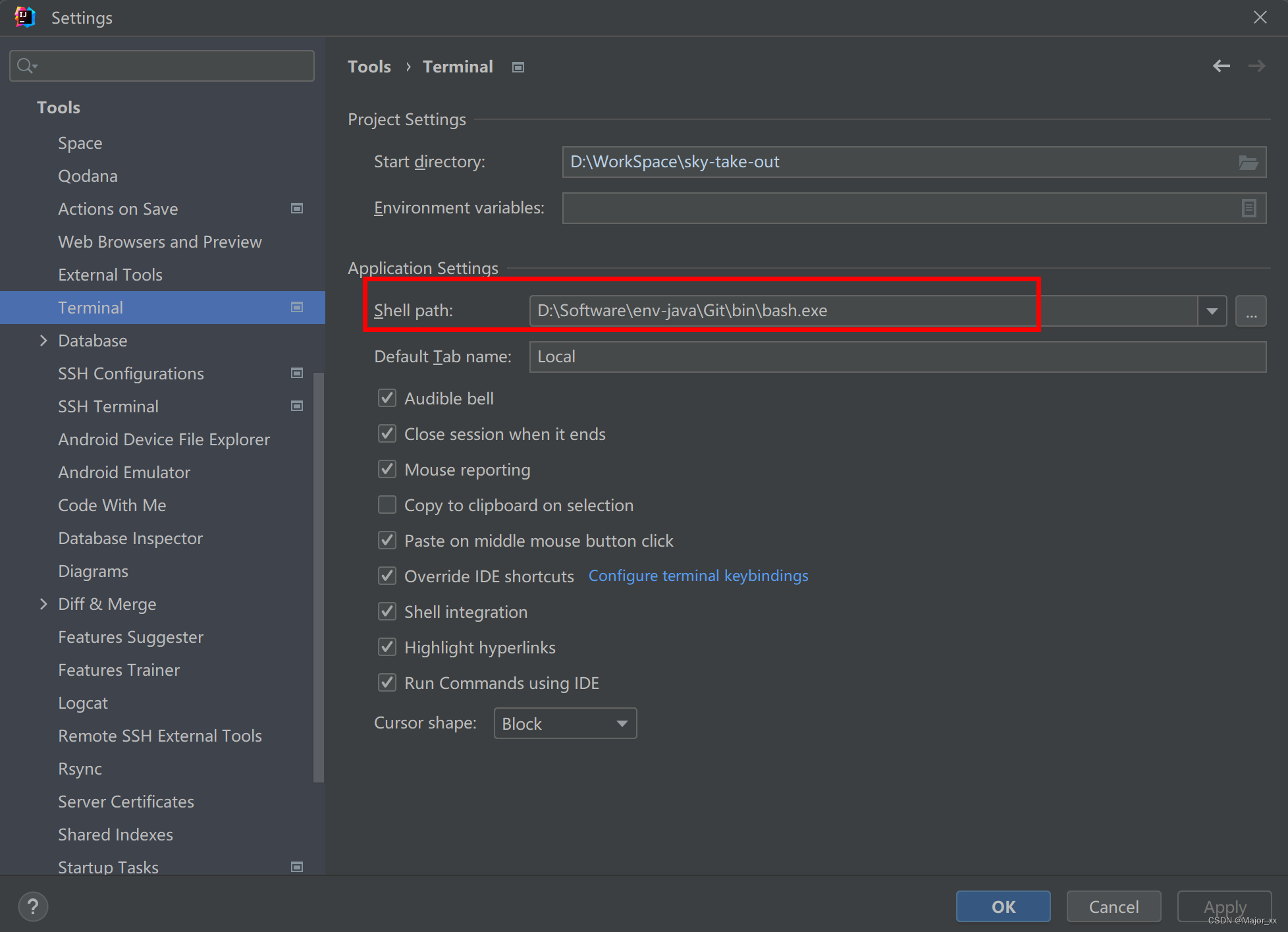
idea设置terminal为git
要在IntelliJ IDEA中设置终端为Git Bash,请按照以下步骤操作: 打开 Settings(设置)。点击 Tools(工具)选项卡。进入 Terminal(终端)界面。在 Shell Path 下选择 Browse(…...

《MySQL 简易速速上手小册》第3章:性能优化策略(2024 最新版)
文章目录 3.1 查询优化技巧3.1.1 基础知识3.1.2 重点案例3.1.3 拓展案例 3.2 索引和查询性能3.2.1 基础知识3.2.2 重点案例3.2.3 拓展案例 3.3 优化数据库结构和存储引擎3.3.1 基础知识3.3.2 重点案例3.3.3 拓展案例 3.1 查询优化技巧 让我们来聊聊如何让你的 MySQL 查询跑得像…...
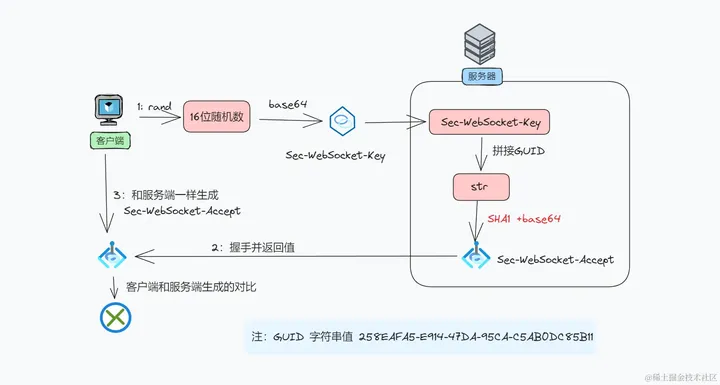
【golang】23、gorilla websocket 源码:examples、数据结构、流程
文章目录 一、examples1.1 echo1.1.1 server.go1.1.2 client.go 1.2 command1.2.1 功能和启动方式1.2.2 home.html1.2.3 main.go 1.3 filewatch1.3.1 html1.3.2 serveHome 渲染模板1.3.3 serveWs1.3.4 writer() 1.4 buffer pool1.4.1 server1.4.2 client 1.5 chat1.5.1 server1…...

SpringCloud+RabbitMQ+Docker+Redis+搜索+分布式 基础(持续更新~)
具体操作: day2: 作用: 出现跨域问题 配相对应进行配置即可解决: IDEA连接的,在url最后加参数?useSSLfalse注意链接密码是123(docker中mysql密码) 注意,虚拟机中设置的密码和ip要和主机上…...
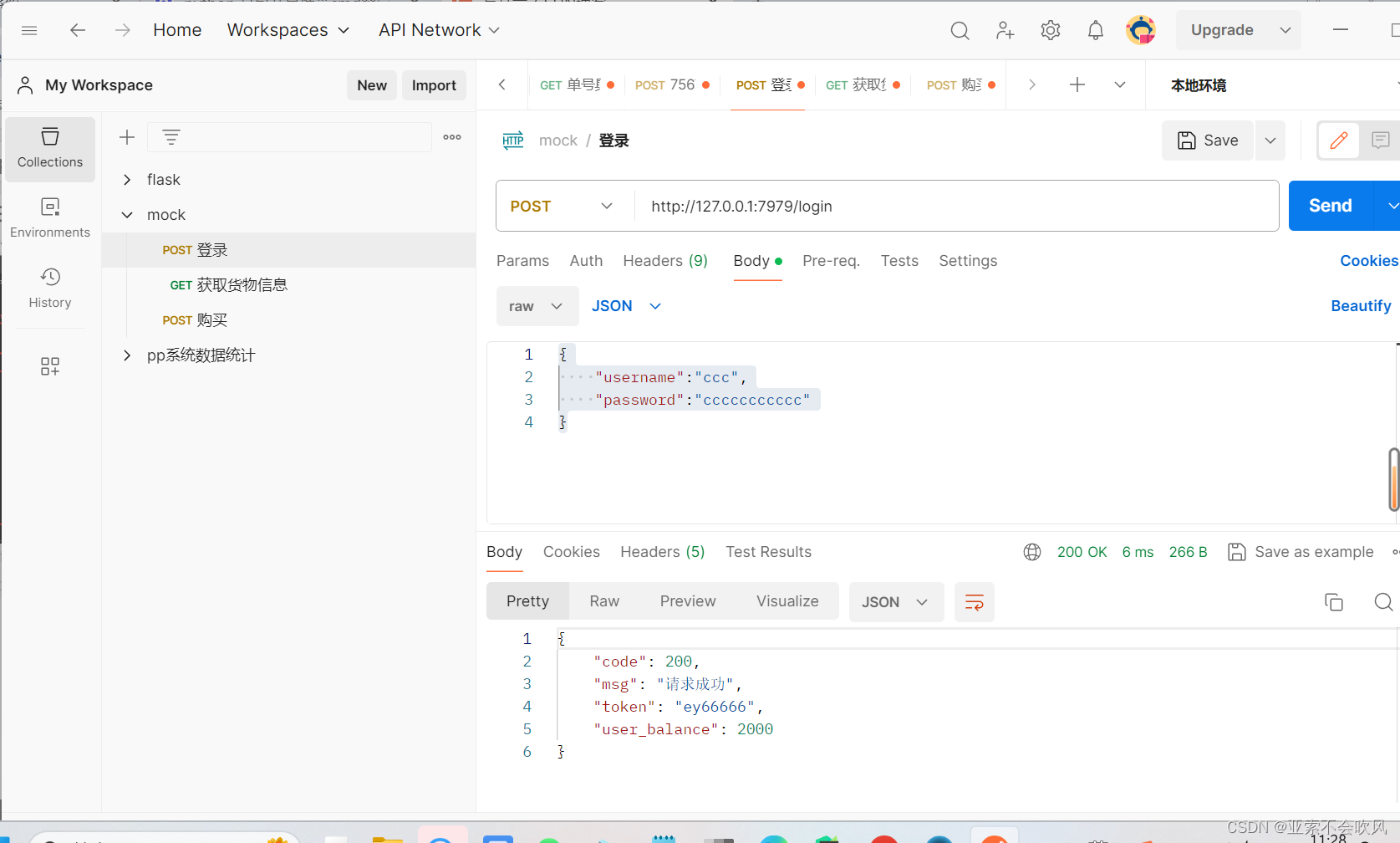
flask+pyinstaller实现mock接口,并打包到exe运行使用postman验证
flask代码 from flask import Flask, request, jsonifyapp Flask(__name__)app.route("/login", methods[POST]) def login():username request.json.get("username").strip() # 用户名password request.json.get("password").strip() # 密…...
【Spring Boot】第一篇 创建简单的Spring Boot项目
导航 一. 简介二. 创建简单的Spring Boot项目1. 工具选择和版本确定2. 创建步骤 三. 部署项目四. 测试验证 一. 简介 Spring Boot是一个用于构建独立的、生产级别的Spring应用程序的框架。它简化了Spring应用程序的创建和配置过程,同时提供了很多开箱即用的功能&am…...

SSL协议是什么?关于SSL和TLS的常见问题解答
SSL(安全套接字层)及其后继者TLS(传输层安全)是用于在联网计算机之间建立经过身份验证和加密的链接的协议。尽管SSL协议在 1999年已经随着TLS 1.0的发布而被弃用,但我们仍将这些相关技术称为“SSL”或“SSL/TLS”。那么…...

第十五个知识:JQuery
初识JQuery: <head><meta charset"UTF-8"><title>Title</title><script src"lib/jquery-3.7.1.js"></script>//引入jquery </head> <body><a href"https://www.baidu.com" id"baidu&q…...

用Matlab 2015a svmtrain函数训练的SVM model在2021b无法使用的解决方法
背景 与r2015a版本的Matlab相比,r2021b版本中包含更多集成好的算法模块(尤其是深度学习的模块),想把原来r2015a版本的代码升级到r2021b高版本的Matlab已经采用fitcsvm函数和predict函数替代了旧版本中svmtrain函数和svmclassify函…...

umount:/home/tuners/windows files:目标忙。
您提到的错误信息 "umount: /home/tuners/windows files: 目标忙。" 是在尝试卸载(umount)一个文件系统时常见的错误。这个错误表明有一些进程仍然在使用挂载点(/home/tuners/windows files)下的文件或目录,…...
FPGA_vga显示
一 VGA 1.1 VGA VGA是视频图像阵列,是一种使用模拟信号进行视频传输的标准协议。 1.2 VGA接引脚定义 VGA分公母两种,RGB显示标准。 1.3 VGA显示器 VGA显示器采用图像扫描的方式进行图像显示,将构成图像的像素点,在行同步信号…...

sklearn模型指标和特征贡献度查看
文章目录 算法介绍r2_scoretrain_test_splitDecisionTreeRegressor参考文献支持快速查看traget和特征之间的关系 # -*- coding: utf-8 -*- import pandas as pd pd.set_option(display.max_columns, None) pd.set_option...
2024.2.6日总结(小程序开发3)
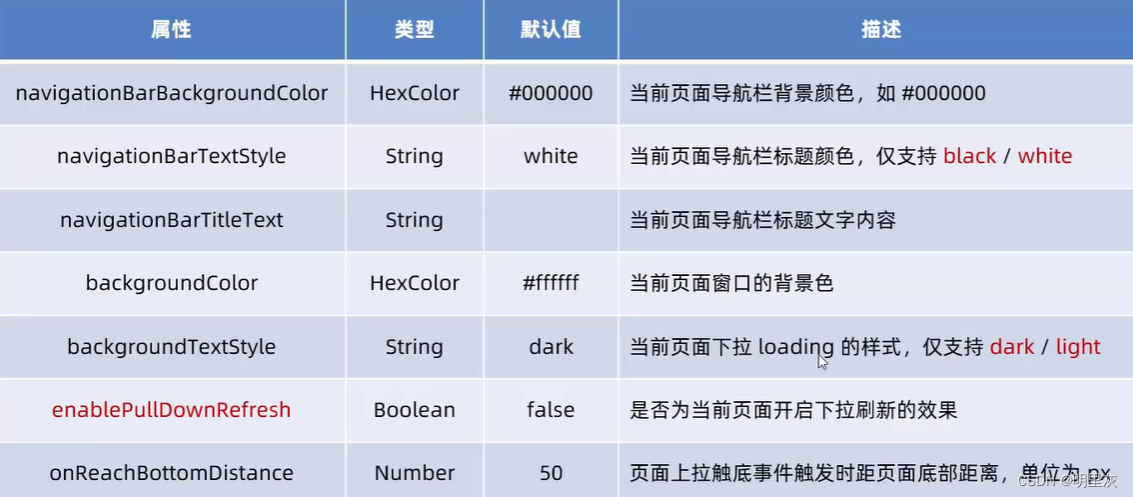
页面配置 页面配置和全局配置的关系: 小程序中,app.json中的window节点,可以全局配置小程序中每个页面的窗口表现 如果某些小程序想要有特殊的窗口表现,可以用页面级别的.json配置文件实现这个需求 页面配置和全局配置冲突时&…...

相机图像质量研究(10)常见问题总结:光学结构对成像的影响--光圈
系列文章目录 相机图像质量研究(1)Camera成像流程介绍 相机图像质量研究(2)ISP专用平台调优介绍 相机图像质量研究(3)图像质量测试介绍 相机图像质量研究(4)常见问题总结:光学结构对成像的影响--焦距 相机图像质量研究(5)常见问题总结:光学结构对成…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
