网课:N皇后问题——牛客(题解和疑问)
题目描述
给出一个n×nn\times nn×n的国际象棋棋盘,你需要在棋盘中摆放nnn个皇后,使得任意两个皇后之间不能互相攻击。具体来说,不能存在两个皇后位于同一行、同一列,或者同一对角线。请问共有多少种摆放方式满足条件。
输入描述:
一行,一个整数n(1≤n≤12)n(1\le n \le 12)n(1≤n≤12),表示棋盘的大小。
输出描述:
输出一行一个整数,表示总共有多少种摆放皇后的方案,使得它们两两不能互相攻击。
示例1
输入
4
输出
2
想法:
就按题意,一个格子一个格子枚举,并看一下有没有行冲突,列冲突,对角线冲突,但结果答案是错的。
代码:
#include<bits/stdc++.h>
using namespace std;
int n;
int ans=0;
int a[15][15];
int st[15][15];
int r[15];//行冲突
int c[15];//列冲突
int djx[2];//对角线冲突
void dfs(int gs){//摆了的皇后个数
//st[x][y]=1;
if(gs>n){
ans++;
return ;
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
//if(st[i][j]) break;
if(r[i]) break;
if(c[j]) continue;
if(djx[0]&&i==j) continue;
if(djx[1]&&i+j==n+1) continue;
r[i]=1;
c[j]=1;
if(i==j){
djx[0]=1;
dfs(gs+1);
djx[0]=0;
}
else if(i+j==n+1){
djx[1]=1;
dfs(gs+1);
djx[1]=0;
}
else dfs(gs+1);
r[i]=0;
c[j]=0;
}
}
}
int main(){
cin>>n;
dfs(0);
cout<<ans;
}
网课:
看了网课后,发现还是有点问题的吧。首先,对角线冲突理解错了,题目指的是每条对角线,而我以为是主对角线和副对角线两条。然后我又想了下怎么标记对角线,找了下对角线的下标有什么规律,emm但也还是想不到怎么表示。网课的提供了两种方法,一种是直接将所有对角线标序号,然后弄个标记数组;第二种就是看规律,主对角线方向上的位于同一条对角线的坐标i+j都是同一个值,副对角线方向上的位于同一条对角线的坐标i-j都是同一个值。利用这点,可以弄两个标记数组。但还有问题,就是副对角线方向上的某些对角线坐标相减是负的,需要把数组下标平移一下。我找规律的时候也有注意到一点点吧,但没那么深刻。还有一点,就是网课的方法搜索时是一行一行搜的,每一行放一个皇后,看是否满足条件,这样直接不用考虑行冲突了。我是一格一格搜索的,复杂度更高。
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=15;
int n;
int ans=0;
int c[N];
int fdjx[N+N-1+N];//平移
int zdjx[N+N-1];
void dfs(int r){//行
if(r>n){
ans++;
return ;
}
for(int i=1;i<=n;i++){//列
if(c[i]) continue;
if(fdjx[r-i+n]) continue;
if(zdjx[r+i]) continue;
c[i]=1;
fdjx[r-i+n]=1;
zdjx[r+i]=1;
dfs(r+1);
c[i]=0;
fdjx[r-i+n]=0;
zdjx[r+i]=0;
}
}
int main(){
cin>>n;
dfs(1);
cout<<ans;
}
修改:
但是吧,我现在按我的想法写,就是一格一格搜索,还是弄不出来。
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=15;
int n;
int ans=0;
int c[N];
int r[N];
int fdjx[N+N-1+N];//平移
int zdjx[N+N-1];
void dfs(int gs){//行
if(gs>n){
ans++;
return ;
}
for(int i=1;i<=n;i++){//列
for(int j=1;j<=n;j++){
if(c[j]) continue;
if(r[i]) break;
if(fdjx[i-j+n]) continue;
if(zdjx[i+j]) continue;
c[j]=1;
r[i]=1;
fdjx[i-j+n]=1;
zdjx[j+i]=1;
dfs(gs+1);
c[i]=0;
r[i]=0;
fdjx[i-j+n]=0;
zdjx[j+i]=0;
}
}
}
int main(){
cin>>n;
dfs(1);
cout<<ans;
}
相关文章:
)
网课:N皇后问题——牛客(题解和疑问)
题目描述 给出一个nnn\times nnn的国际象棋棋盘,你需要在棋盘中摆放nnn个皇后,使得任意两个皇后之间不能互相攻击。具体来说,不能存在两个皇后位于同一行、同一列,或者同一对角线。请问共有多少种摆放方式满足条件。 输入描述: …...
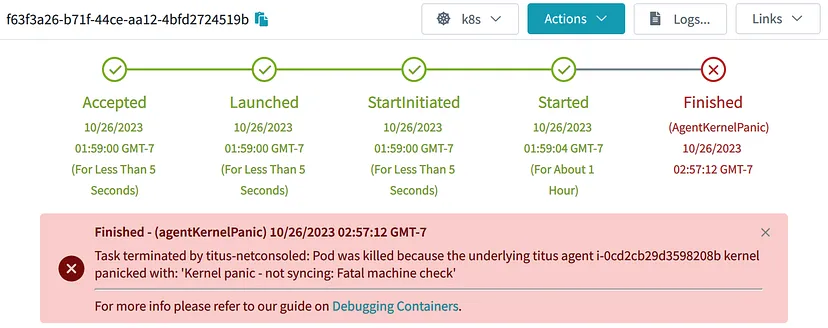
[大厂实践] Netflix容器平台内核panic可观察性实践
在某些情况下,K8S节点和Pod会因为出错自动消失,很难追溯原因,其中一种情况就是发生了内核panic。本文介绍了Netflix容器平台针对内核panic所做的可观测性增强,使得发生内核panic的时候,能够导出信息,帮助排…...

2024/2/8
数据类型与作用域练习 1、选择题 1.1、以下选项中,不能作为合法常量的是 ___b_______ A)1.234e04 B)1.234e0.4 C)1.234e4 D)1.234e0 1.2、以下定义变量并初始化错误的是______d_______。 A) char c1 ‘H’ &am…...
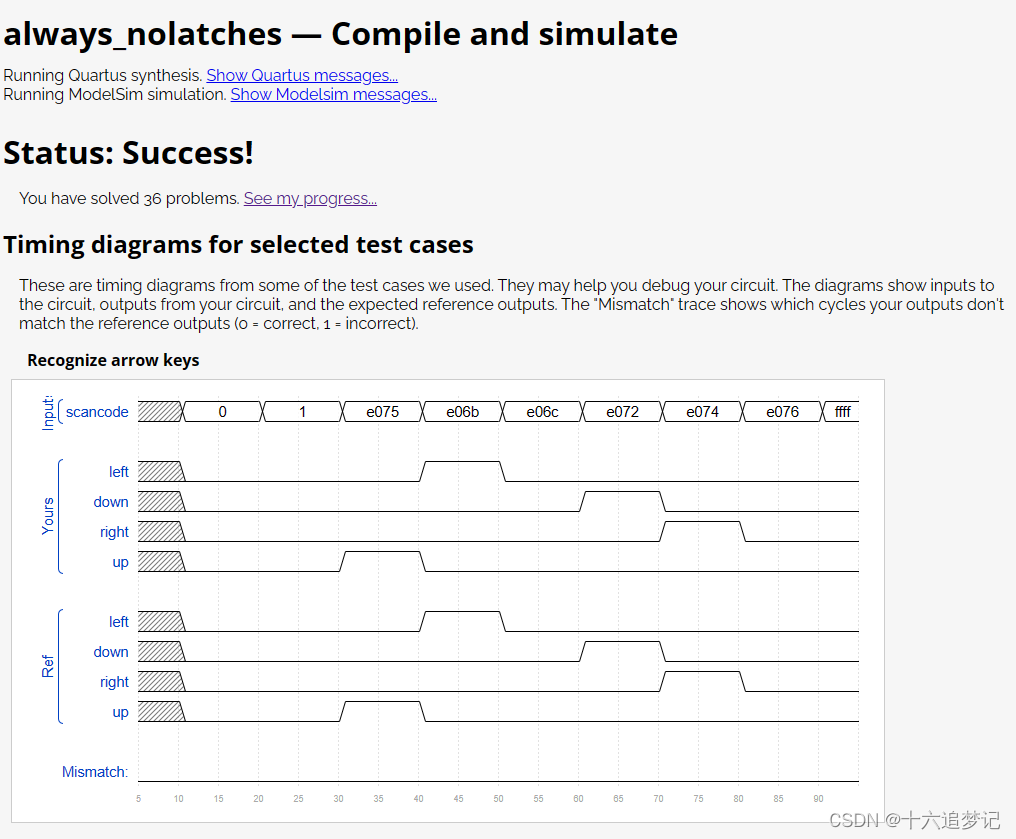
Verilog刷题笔记23
题目: Suppose you’re building a circuit to process scancodes from a PS/2 keyboard for a game. Given the last two bytes of scancodes received, you need to indicate whether one of the arrow keys on the keyboard have been pressed. This involves a fairly simp…...
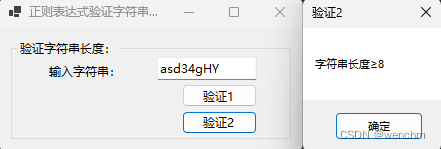
C#验证字符串的长度,用正则表达式 vs 字符数组长度或字符串的长度
目录 一、使用的方法 1.使用正则表达式 2.通过计算字符串的长度验证 二、实例 1.源码 2.生成效果 一、使用的方法 1.使用正则表达式 使用正则表达式可以判断和限制用户输入的字符串长度。 比如验证用户密码不得少于8为,匹配的正则表达式"^.{8,}$"…...

opencv C++ dnn模块调用yolov5以及Intel RealSense D435深度相机联合使用进行目标检测
一、代码 #include <opencv2/opencv.hpp> #include <opencv2/dnn/dnn.hpp> #include <librealsense2/rs.hpp> // Include RealSense Cross Platform APIusing namespace cv; using namespace dnn; using namespace std; using namespace rs2;// 类名数组&am…...
2024牛客寒假算法基础集训营1(视频讲解全部题目)
2024牛客寒假算法基础集训营1(题目全解) ABCDEFGHIJKLM 2024牛客寒假算法基础集训营1(视频讲解全部题目) A #include<bits/stdc.h> #define endl \n #define deb(x) cout << #x << " " << …...

第三百一十三回
文章目录 1. 概念介绍2. 实现方法2.1 obscureText属性2.2 decoration属性 3. 示例代码4. 内容总结 我们在上一章回中介绍了"如何实现倒计时功能"相关的内容,本章回中将介绍如何实现密码输入框.闲话休提,让我们一起Talk Flutter吧。 1. 概念介绍…...
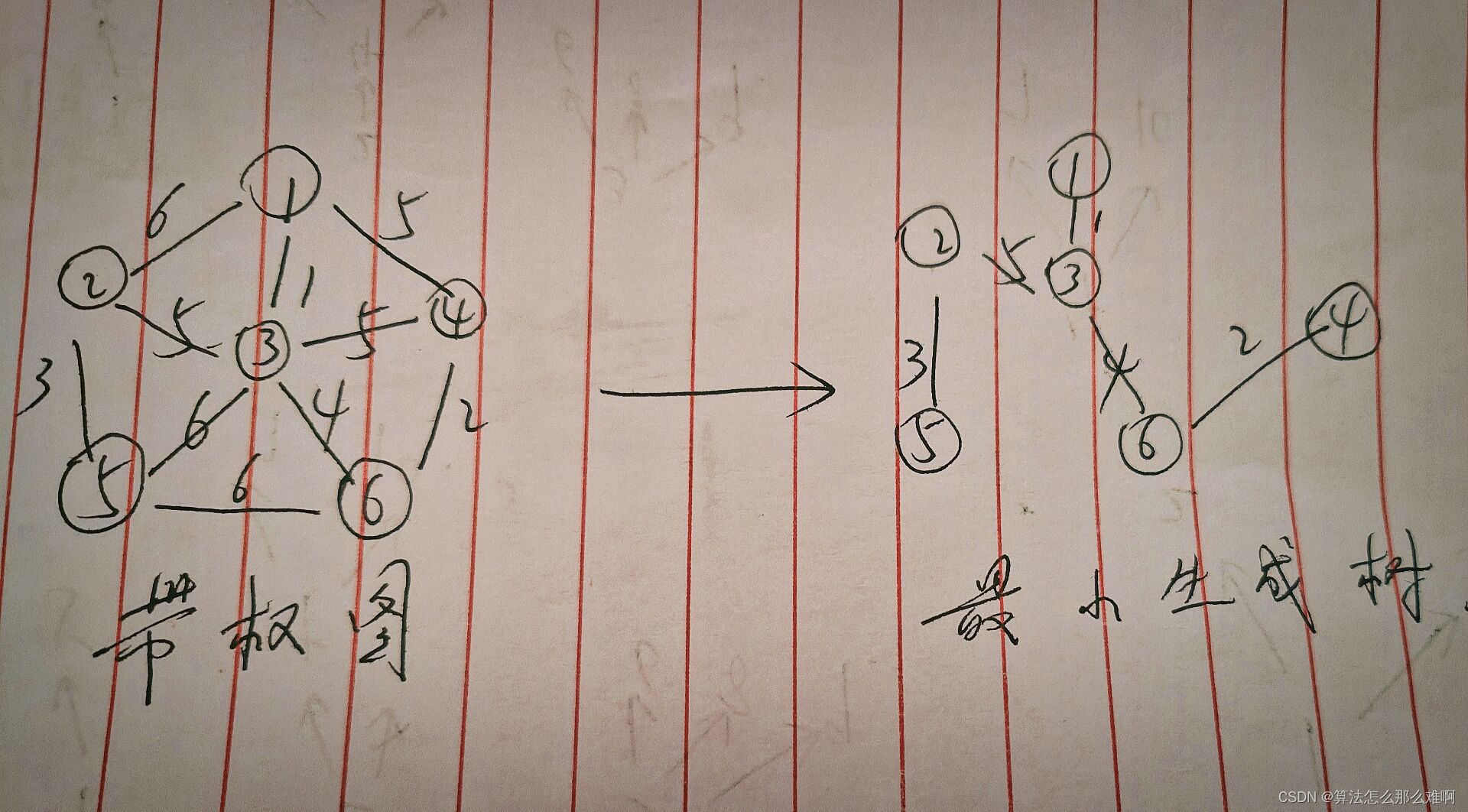
倒计时61天
M-智乃的36倍数(normal version)_2024牛客寒假算法基础集训营3 (nowcoder.com) //非ac代码,超时了,54.17/100#include<bits/stdc.h> using namespace std; const int N1e55; const int inf0x3f3f3f3f; #define int long long int n; string s1[N]; void solve() {cin>…...
)
npm后Truffle找不到命令(ubantu20系统)
Truffle找不到命令 方法1方法2 方法1 # 编辑.profile vim ~/.profile # 在.profile末尾把nodejs的解压路径添加到$PATH环境变量中 PATH"$HOME/bin:$HOME/.local/bin:路径:$PATH" source 文件方法2 #ls -l 在nodejs的bin目录下查看truffle链接的脚本文件 truffle -&…...
嵌入式学习第三篇——51单片机
目录 1,嵌入式系统 1,嵌入式系统的定义 2,单片机的定义 2,51单片机 1,开发环境 2,开发板使用的基本思路 1,查看原理图,查看芯片手册 2,获得调用硬件的管…...
RabbitMQ详解
RabbitMQ 1.初识MQ 1.1.同步和异步通讯 微服务间通讯有同步和异步两种方式: 同步通讯:就像打电话,需要实时响应。 异步通讯:就像发邮件,不需要马上回复。 两种方式各有优劣,打电话可以立即得到响应&a…...

CGAL::2D Arrangements-4
4. Free函数 Arrangement_on_surface_2类模板是用曲线切分二维的面。因为它的接口设计是最简化的,这意味着它的成员函数很少执行几何操作。本章将解释怎么利用这些Free function来达到Arrangement操作。执行这些操作通常需要优秀的几何算法,而且有时会对…...
终端命令提示符:如何查看我们电脑端口是否被占用和处理方式
文章目录 端口信息查看1、Windows:2、Linux/macOS: 使用 netstat使用 lsof 端口信息查看 在不同的操作系统中,查看端口是否被占用的指令有所不同。以下是一些常见的指令: 1、Windows: 使用命令行工具 netstat 来查看端口占用情况。 电脑键盘按住 win…...
elasticsearch重置密码操作
安装es的时候需要测试这个url:http://127.0.0.1:9200/ 出现弹窗让我输入账号和密码。我第一次登录,没有设置过账号和密码, 解决方法是:在es的bin目录下打开cmd窗口,敲命令:.\elasticsearch-reset-password…...
—— 导航)
从零开始手写mmo游戏从框架到爆炸(零)—— 导航
从今天开始我们尝试从零开始写一个mmo的游戏。主要技术还是netty。参考了网上很多的大神的框架,本来希望基于ioGame或者vert.x等来直接写功能的,觉得从零开始更有意义,而且咱们也不需要太NB的底层功能,够用就行。 下面是导航&…...
)
机器学习7-K-近邻算法(K-NN)
K-Nearest Neighbors(K-近邻算法,简称KNN)是一种基本的监督学习算法,用于解决分类和回归问题。KNN的核心思想是基于距离度量,在特征空间中找到最近的K个样本,然后使用它们的标签进行决策。以下是KNN的基本概…...

相机图像质量研究(7)常见问题总结:光学结构对成像的影响--镜片固化
系列文章目录 相机图像质量研究(1)Camera成像流程介绍 相机图像质量研究(2)ISP专用平台调优介绍 相机图像质量研究(3)图像质量测试介绍 相机图像质量研究(4)常见问题总结:光学结构对成像的影响--焦距 相机图像质量研究(5)常见问题总结:光学结构对成…...

猫头虎分享已解决Bug || Go Error: cannot convert int to string
博主猫头虎的技术世界 🌟 欢迎来到猫头虎的博客 — 探索技术的无限可能! 专栏链接: 🔗 精选专栏: 《面试题大全》 — 面试准备的宝典!《IDEA开发秘籍》 — 提升你的IDEA技能!《100天精通鸿蒙》 …...

前端bug手册
JavaScript错误:常见的JavaScript错误包括语法错误、未定义的变量、类型错误等。这些错误可能导致页面无法正常运行或功能无法正常使用。样式问题:前端开发中常见的样式问题包括布局错乱、元素位置不正确、样式覆盖等。这些问题可能导致页面显示不正常或…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
如何做好一份技术文档?从规划到实践的完整指南
如何做好一份技术文档?从规划到实践的完整指南 🌟 嗨,我是IRpickstars! 🌌 总有一行代码,能点亮万千星辰。 🔍 在技术的宇宙中,我愿做永不停歇的探索者。 ✨ 用代码丈量世界&…...
