LeetCode983. Minimum Cost For Tickets——动态规划
文章目录
- 一、题目
- 二、题解
一、题目
You have planned some train traveling one year in advance. The days of the year in which you will travel are given as an integer array days. Each day is an integer from 1 to 365.
Train tickets are sold in three different ways:
a 1-day pass is sold for costs[0] dollars,
a 7-day pass is sold for costs[1] dollars, and
a 30-day pass is sold for costs[2] dollars.
The passes allow that many days of consecutive travel.
For example, if we get a 7-day pass on day 2, then we can travel for 7 days: 2, 3, 4, 5, 6, 7, and 8.
Return the minimum number of dollars you need to travel every day in the given list of days.
Example 1:
Input: days = [1,4,6,7,8,20], costs = [2,7,15]
Output: 11
Explanation: For example, here is one way to buy passes that lets you travel your travel plan:
On day 1, you bought a 1-day pass for costs[0] = $2, which covered day 1.
On day 3, you bought a 7-day pass for costs[1] = $7, which covered days 3, 4, …, 9.
On day 20, you bought a 1-day pass for costs[0] = $2, which covered day 20.
In total, you spent $11 and covered all the days of your travel.
Example 2:
Input: days = [1,2,3,4,5,6,7,8,9,10,30,31], costs = [2,7,15]
Output: 17
Explanation: For example, here is one way to buy passes that lets you travel your travel plan:
On day 1, you bought a 30-day pass for costs[2] = $15 which covered days 1, 2, …, 30.
On day 31, you bought a 1-day pass for costs[0] = $2 which covered day 31.
In total, you spent $17 and covered all the days of your travel.
Constraints:
1 <= days.length <= 365
1 <= days[i] <= 365
days is in strictly increasing order.
costs.length == 3
1 <= costs[i] <= 1000
二、题解
class Solution {
public:int mincostTickets(vector<int>& days, vector<int>& costs) {vector<int> durations = {1,7,30};int n = days.size();vector<int> dp(n+1,INT_MAX);dp[n] = 0;for(int i = n - 1;i >= 0;i--){for(int k = 0,j = i;k < 3;k++){while(j < n && days[i] + durations[k] > days[j]) j++;dp[i] = min(dp[i],costs[k] + dp[j]);}}return dp[0];}
};
相关文章:

LeetCode983. Minimum Cost For Tickets——动态规划
文章目录 一、题目二、题解 一、题目 You have planned some train traveling one year in advance. The days of the year in which you will travel are given as an integer array days. Each day is an integer from 1 to 365. Train tickets are sold in three differen…...
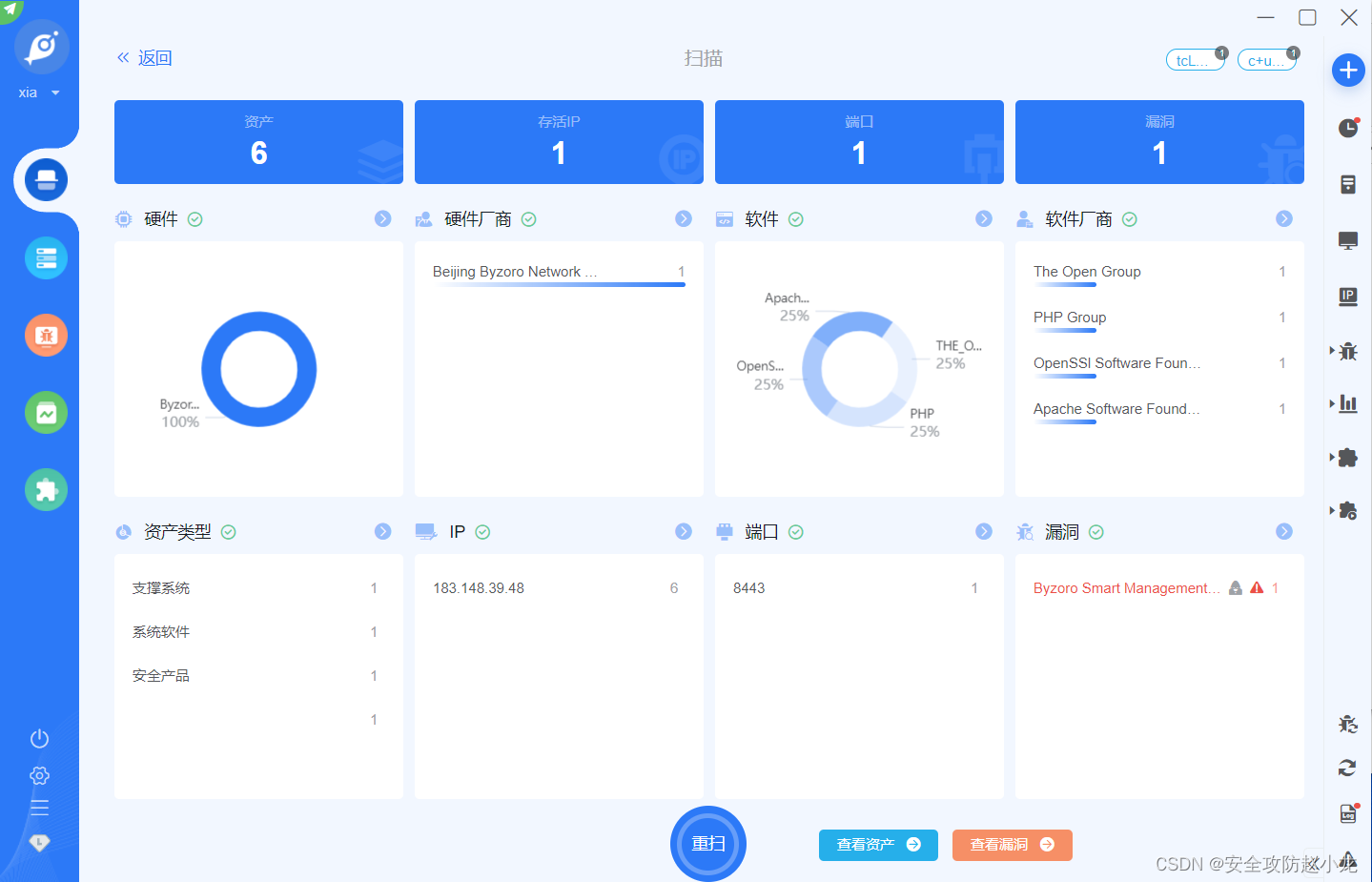
百卓Smart管理平台 uploadfile.php 文件上传漏洞【CVE-2024-0939】
百卓Smart管理平台 uploadfile.php 文件上传漏洞【CVE-2024-0939】 一、 产品简介二、 漏洞概述三、 影响范围四、 复现环境五、 漏洞复现手动复现小龙验证Goby验证 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工…...

项目中常用的一些数据库及缓存
1、常见的开发工具介绍 MySQL: MySQL是一种流行的开源关系型数据库管理系统(RDBMS),由瑞典MySQL AB公司开发,并在后来被Sun Microsystems收购,最终成为Oracle公司的一部分。MySQL广泛用于各种Web应用程序和大型企业应…...
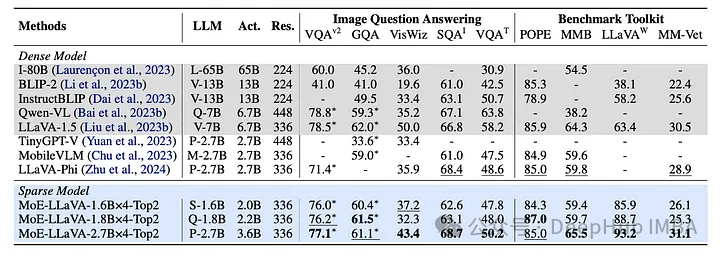
MoE-LLaVA:具有高效缩放和多模态专业知识的大型视觉语言模型
视觉和语言模型的交叉导致了人工智能的变革性进步,使应用程序能够以类似于人类感知的方式理解和解释世界。大型视觉语言模型(LVLMs)在图像识别、视觉问题回答和多模态交互方面提供了无与伦比的能力。 MoE-LLaVA利用了“专家混合”策略融合视觉和语言数据࿰…...

【Java】ArrayList和LinkedList的区别是什么
目录 1. 数据结构 2. 性能特点 3. 源码分析 4. 代码演示 5. 细节和使用场景 ArrayList 和 LinkedList 分别代表了两类不同的数据结构:动态数组和链表。它们都实现了 Java 的 List 接口,但是有着各自独特的特点和性能表现。 1. 数据结构 ArrayList…...
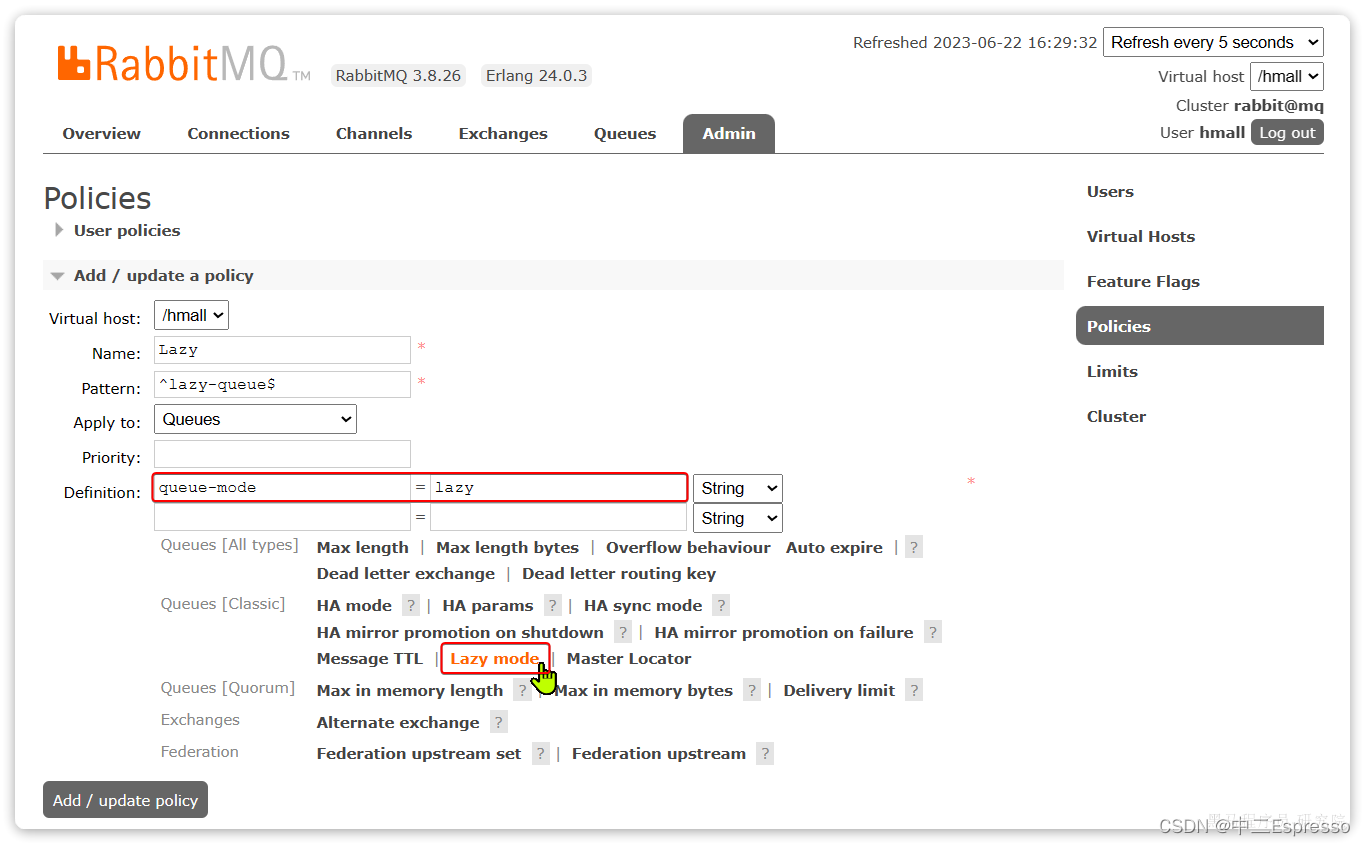
RabbitMQ-4.MQ的可靠性
MQ的可靠性 4.MQ的可靠性4.1.数据持久化4.1.1.交换机持久化4.1.2.队列持久化4.1.3.消息持久化 4.2.LazyQueue4.2.1.控制台配置Lazy模式4.2.2.代码配置Lazy模式4.2.3.更新已有队列为lazy模式 4.MQ的可靠性 消息到达MQ以后,如果MQ不能及时保存,也会导致消…...

编程相关的经典的网站和书籍
经典网站: Stack Overflow:作为全球最大的程序员问答社区,Stack Overflow 汇聚了大量的编程问题和解答,为程序员提供了极大的帮助。GitHub:全球最大的开源代码托管平台,程序员可以在上面共享自己的项目代码…...

Java代码实现基数排序算法(附带源码)
基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数。 1. 基数排序…...
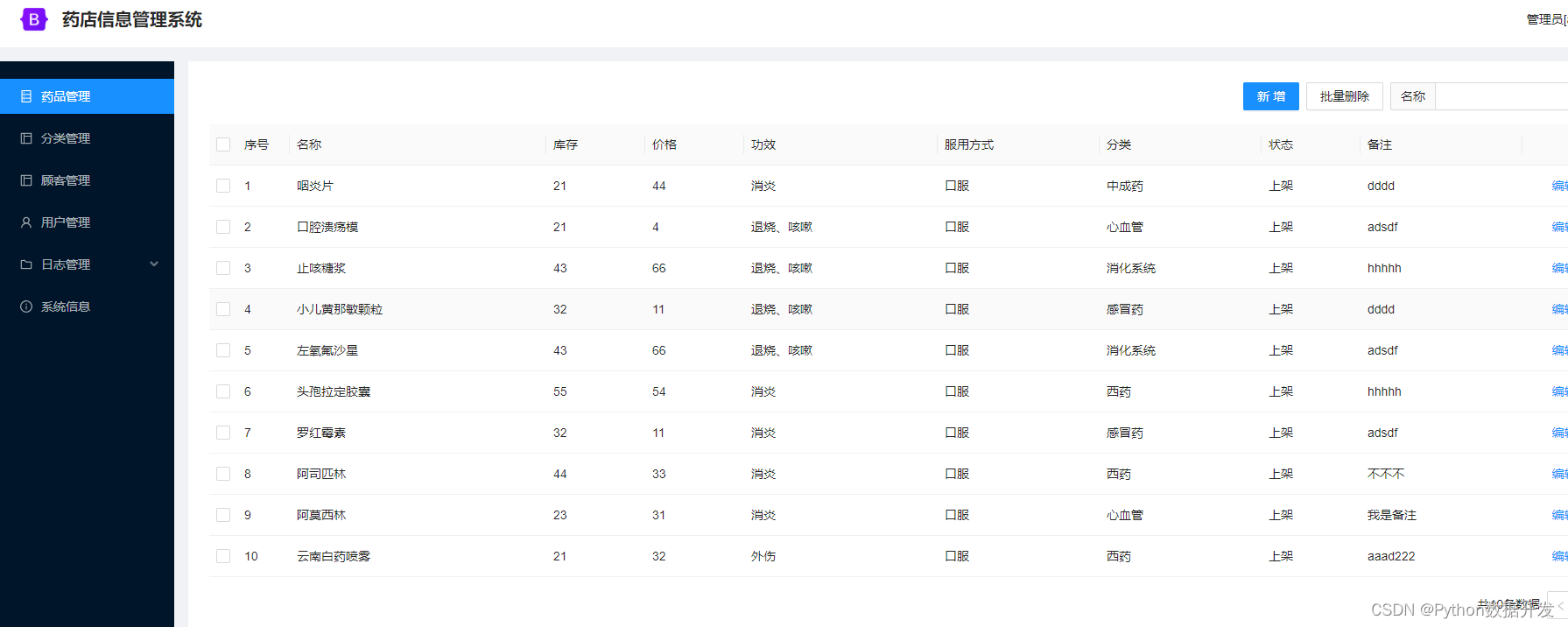
基于python+django,我开发了一款药店信息管理系统
功能介绍 平台采用B/S结构,后端采用主流的Python语言进行开发,前端采用主流的Vue.js进行开发。 功能包括:药品管理、分类管理、顾客管理、用户管理、日志管理、系统信息模块。 代码结构 server目录是后端代码web目录是前端代码 部署运行…...
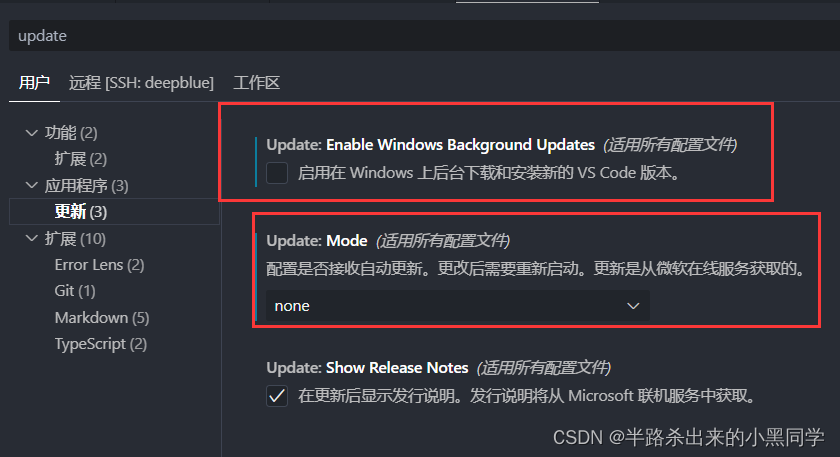
VSCODE使用ssh远程连接时启动服务器失败问题
错误情况 ping服务器的ip可通并且使用terminal可以ssh连接到远程服务器。但使用vscode的remote-ssh时,在「输出」栏出现了一直报 Waiting for server log… 的情况! 解决方法一 重置服务器设置,包括以下手段: 1.清理服务器端的…...

easyexcle 导出csv
导入jar <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>3.3.3</version></dependency>代码 private static List<List<String>> head() {List<List<String>&g…...
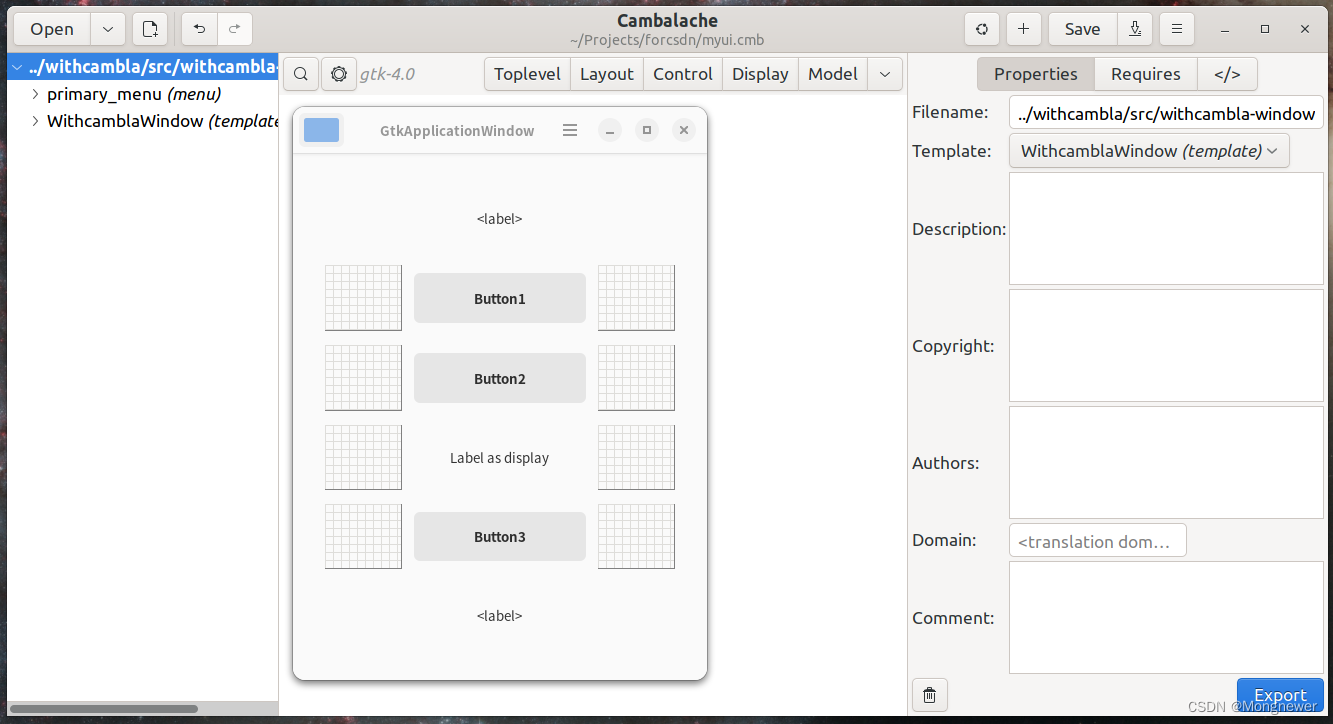
Ubuntu22.04 gnome-builder gnome C 应用程序习练笔记(一)
一、序言 gnome-builder构建器是gnome程序开发的集成环境,支持主力语言C, C, Vala, jscript, python等,界面以最新的 gtk 4.12 为主力,将其下版本的gtk直接压入了depreciated,但gtk4.12与普遍使用的gtk3有很大区别,原…...

ESP32QRCodeReader库使用,ESP32-CAM识别二维码并向自写接口发出请求确认身份。
#include <Arduino.h> #include <WiFi.h> #include <HTTPClient.h> #include <ESP32QRCodeReader.h>#define WIFI_SSID "username" #define WIFI_PASSWORD "password" // 连接电脑主机的IP地址的8088端口 #define WEBHOOK_URL &qu…...

什么是网络渗透,应当如何防护?
什么是网络渗透 网络渗透是攻击者常用的一种攻击手段,也是一种综合的高级攻击技术,同时网络渗透也是安全工作者所研究的一个课题,在他们口中通常被称为"渗透测试(Penetration Test)"。无论是网络渗透(Network Penetration)还是渗透…...

掌握C++中的动态数据:深入解析list的力量与灵活性
1. 引言 简介std::list和其在C中的角色 std::list是C标准模板库(STL)中提供的一个容器类,实现了双向链表的数据结构。与数组或向量等基于连续内存的容器不同,std::list允许非连续的内存分配,使得元素的插入和删除操作…...
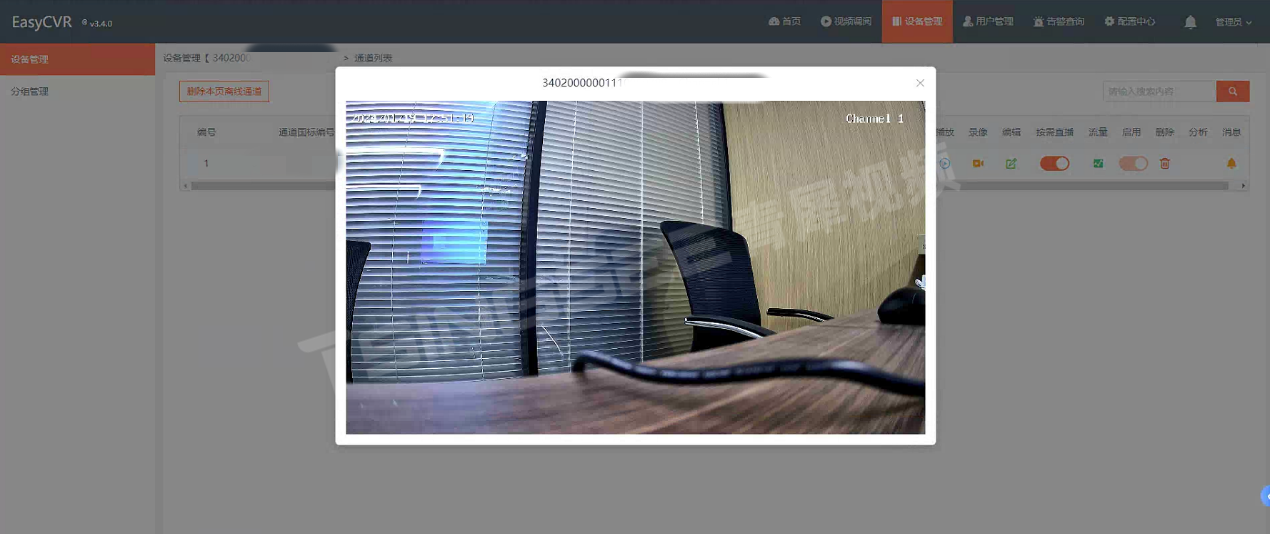
天地伟业接入视频汇聚/云存储平台EasyCVR详细步骤
安防视频监控/视频集中存储/云存储/磁盘阵列EasyCVR平台可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等,以及支持厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等。平台既具备传统安…...
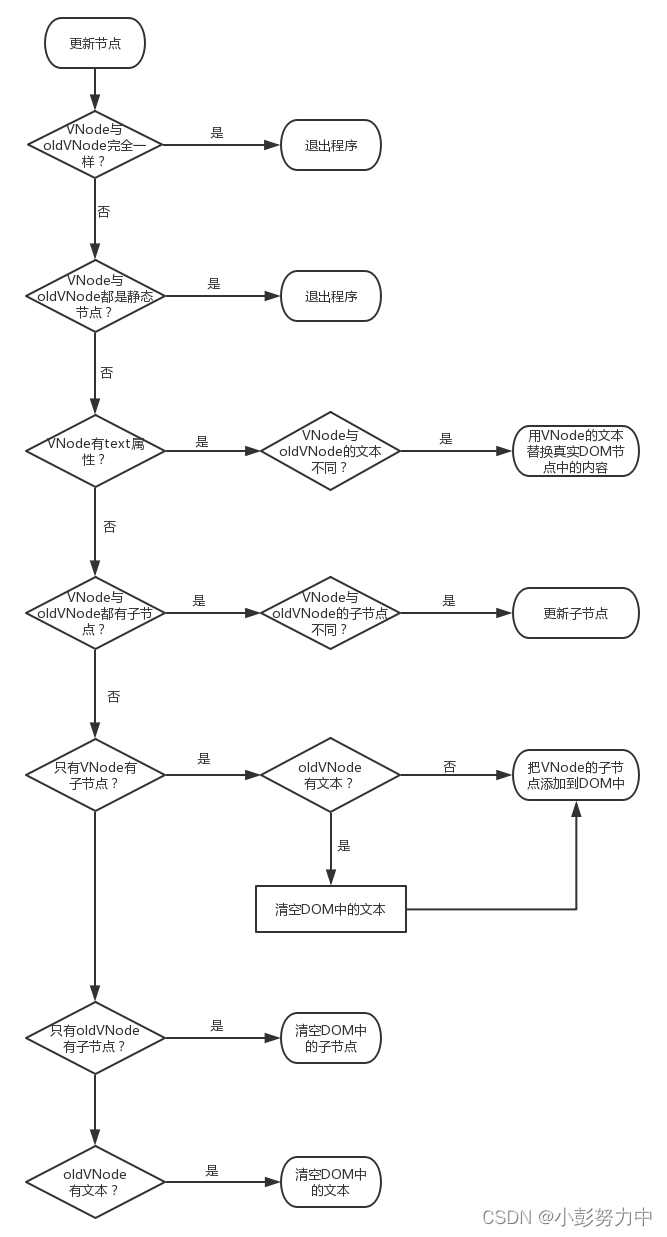
Vue源码系列讲解——虚拟DOM篇【二】(Vue中的DOM-Diff)
目录 1. 前言 2. patch 3. 创建节点 4. 删除节点 5. 更新节点 6. 总结 1. 前言 在上一篇文章介绍VNode的时候我们说了,VNode最大的用途就是在数据变化前后生成真实DOM对应的虚拟DOM节点,然后就可以对比新旧两份VNode,找出差异所在&…...
基于AST实现一键自动提取替换国际化文案
背景:在调研 formatjs/cli 使用(使用 formatjs/cli 进行国际化文案自动提取 )过程中,发现有以下需求formatjs/cli 无法满足: id 需要一定的语义化; defaultMessage和Id不能直接hash转换; 需要…...

嵌入式硬件工程师与嵌入式软件工程师
嵌入式硬件工程师与嵌入式软件工程师 纯硬件设备与嵌入式设备 纯硬件设备是指内部不包含微处理器,无需烧写软件就能够运行的电子设备。如天线、老式收音机、老式电视机、老式洗衣机等。这类设备通常功能简单,易于操作,用户通常只需要打开电…...
【华为云】云上两地三中心实践实操
写在前面 应用上云之后,如何进行数据可靠性以及业务连续性的保障是非常关键的,通过华为云云上两地三中心方案了解相关方案认证地址:https://connect.huaweicloud.com/courses/learn/course-v1:HuaweiXCBUCNXI057Self-paced/about当前内容为华…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...
