1123. 铲雪车(欧拉回路)
随着白天越来越短夜晚越来越长,我们不得不考虑铲雪问题了。
整个城市所有的道路都是双向车道,道路的两个方向均需要铲雪。因为城市预算的削减,整个城市只有 1 辆铲雪车。
铲雪车只能把它开过的地方(车道)的雪铲干净,无论哪儿有雪,铲雪车都得从停放的地方出发,游历整个城市的街道。
现在的问题是:最少要花多少时间去铲掉所有道路上的雪呢?
输入格式
输入数据的第 1 行表示铲雪车的停放坐标 (x,y),x,y 为整数,单位为米。
下面最多有4000行,每行给出了一条街道的起点坐标和终点坐标,坐标均为整数,所有街道都是笔直的,且都是双向车道。
铲雪车可以在任意交叉口、或任何街道的末尾任意转向,包括转 U 型弯。
铲雪车铲雪时前进速度为 20 千米/时,不铲雪时前进速度为 50 千米/时。
保证:铲雪车从起点一定可以到达任何街道。
输出格式
输出铲掉所有街道上的雪并且返回出发点的最短时间,精确到分钟,四舍五入到整数。
输出格式为”hours:minutes”,minutes不足两位数时需要补前导零。
具体格式参照样例。
数据范围
−106≤x,y≤106
所有位置坐标绝对值不超过 106
输入样例:
0 0
0 0 10000 10000
5000 -10000 5000 10000
5000 10000 10000 10000
输出样例:
3:55
样例解释
输出结果表示共需3小时55分钟。
解析:
一、在无向图中(所有边都是连通的):
(1)存在欧拉路径的充分必要条件:度数为奇数的点只能有0或2。
(2)存在欧拉回路(起点和终点相同)的充分必要条件:度数为奇数的点只能有0个。
二、在有向图中(所有边都是连通的):
(1)存在欧拉路径的充分必要条件:要么所有点的入度均等于入度;要么除了两个点之外,其余所有的点的出度等于入度,剩余的两个点:一个满足出度比入度多1(起点),另一个满足入度比出度多1(终点)。
(2)存在欧拉回路(起点和终点相同)的充分必要条件:所有点的入度均等于出度。
欧拉回路的dfs用边来判重,不能用点。
本题根据存在欧拉回路(起点和终点相同)的充分必要条件,易知一定存在欧拉回路,所以答案就是街道距离乘2除以 20 千米/时。
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
#include<unordered_map>
#include<unordered_set>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
const int N = 2e2 + 5, M = 2e5 + 5, INF = 0x3f3f3f3f;int main() {double x1, y1, x2, y2;cin >> x1 >> y1;double sum = 0;;while (cin >> x1 >> y1 >> x2 >> y2) {double dx = x1 - x2;double dy = y1 - y2;sum += sqrt(dx * dx + dy * dy)*2;}int minu = round(sum / 1000 / 20 * 60);int h = minu / 60;minu %= 60;printf("%d:%02d\n", h , minu);return 0;
}相关文章:
)
1123. 铲雪车(欧拉回路)
活动 - AcWing 随着白天越来越短夜晚越来越长,我们不得不考虑铲雪问题了。 整个城市所有的道路都是双向车道,道路的两个方向均需要铲雪。因为城市预算的削减,整个城市只有 1 辆铲雪车。 铲雪车只能把它开过的地方(车道)的雪铲干…...
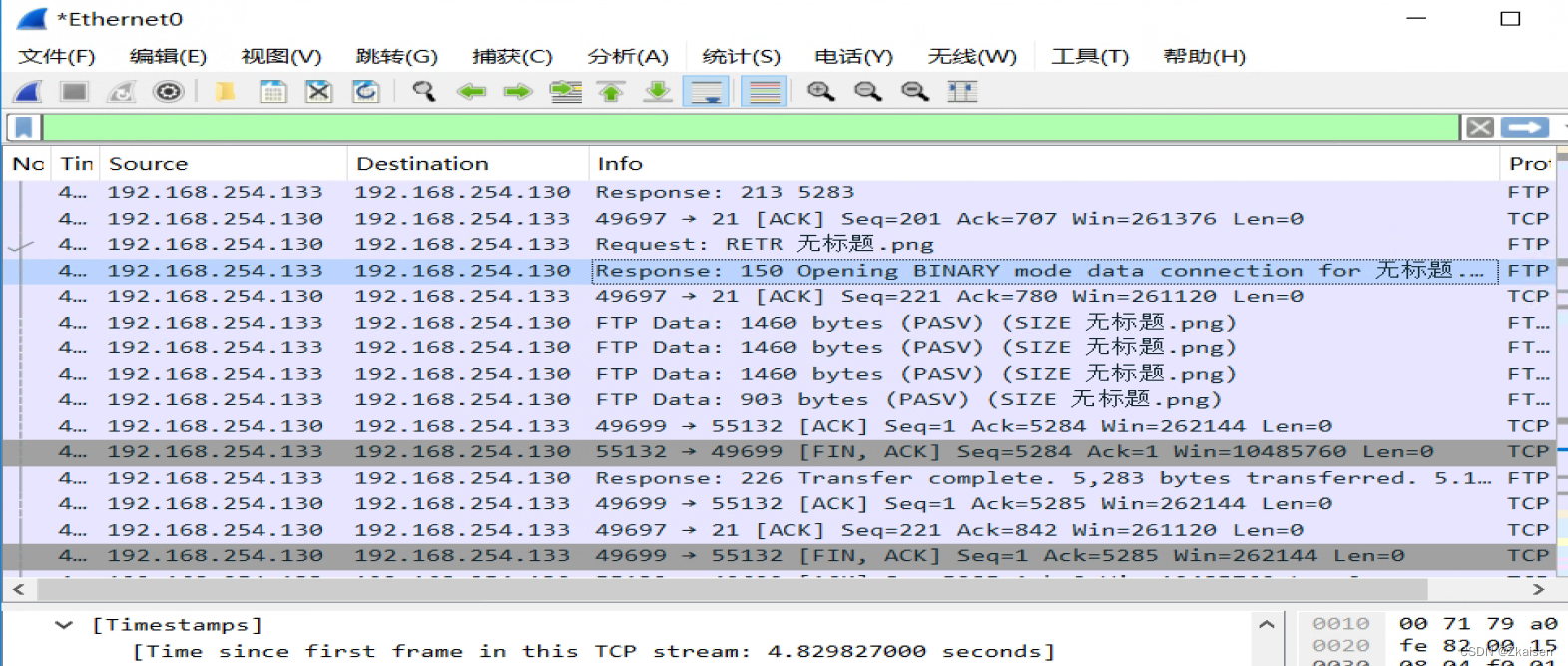
网络协议与攻击模拟_15FTP协议
了解FTP协议 在Windows操作系统上使用serv-U软件搭建FTP服务 分析FTP流量 一、FTP协议 1、FTP概念 FTP(文件传输协议)由两部分组成:客户端/服务端(C/S架构) 应用场景:企业内部存放公司文件、开发网站时利…...

「效果图渲染」效果图与3D影视动画渲染平台
效果图渲染和3D影视动画渲染都是视觉图像渲染的领域应用。效果图渲染主要服务于建筑、室内设计和产品设计等行业,这些领域通常对视觉呈现的精度和细节有较高要求。与之相比,3D影视动画渲染则普遍应用于电影、电视、视频游戏和广告等媒体领域,…...

Blender_查看版本
Blender_查看版本 烦人的烦恼,没找见哪儿可以查看版本? 算是个隐蔽的角落!...

node.js 读目录.txt文件,用 xml2js 转换为json数据,生成jstree所需的文件
请参阅:java : pdfbox 读取 PDF文件内书签 请注意:书的目录.txt 编码:UTF-8,推荐用 Notepad 转换编码。 npm install elementtree ; npm install xml2js ; node.js 用 elementtree读目录.txt文件,用 xml2js 转换为…...

【Docker】02 镜像管理
文章目录 一、Images镜像二、管理操作2.1 搜索镜像2.1.1 命令行搜索2.1.2 页面搜索2.1.3 搜索条件 2.2 下载镜像2.3 查看本地镜像2.3.1 docker images2.3.2 --help2.3.3 repository name2.3.4 --filter2.3.5 -q2.3.6 --format 2.4 给镜像打标签2.5 推送镜像2.6 删除镜像2.7 导出…...

了解海外云手机的多种功能
随着社会的高度发展,海外云手机成为商家不可或缺的工具,为企业出海提供了便利的解决方案。然而,谈及海外云手机,很多人仍不了解其强大功能。究竟海外云手机有哪些功能,可以为我们做些什么呢? 由于国内电商竞…...

白酒:自动化生产线的优势与实践
随着科技的进步,自动化生产线在各行各业的应用越来越广泛。云仓酒庄的豪迈白酒在生产过程中,也积极引入自动化生产线,以提升生产效率、品质和安全性。 首先,自动化生产线能够显著提高生产效率。传统的手工生产线在生产过程中容易受…...
用HTML5实现灯笼效果
本文介绍了两种实现效果:一种使用画布(canvas)标签/元素,另一种不用画布(canvas)标签/元素主要使用CSS实现。 使用画布(canvas)标签/元素实现,下面,在画布上…...
事务XID分配与主备XID同步)
Postgresql源码(120)事务XID分配与主备XID同步
参考 《Postgresql源码(25)子事务可见性判断和性能问题》 XID获取顶层入口 函数:AssignTransactionId static void AssignTransactionId(TransactionState s) {...优先给没有事务ID的父事务分配 确保父事务有 XID,以便子事务总是…...
)
B2077 角谷猜想(洛谷)
题目描述 所谓角谷猜想,是指对于任意一个正整数,如果是奇数,则乘 33 加 11,如果是偶数,则除以 22,得到的结果再按照上述规则重复处理,最终总能够得到 11。如,假定初始整数为 55&…...

排序算法---归并排序
原创不易,转载请注明出处。欢迎点赞收藏~ 归并排序是一种常见的排序算法,它采用了分治的思想。它将一个待排序的数组递归地分成两个子数组,分别对两个子数组进行排序,然后将排好序的子数组合并成一个有序数组。 具体的归并排序过…...

[WUSTCTF2020]朴实无华(特详解)
一开始说header出问题了 就先dirsaerch扫一遍 发现robot.txt 访问一下 去看看,好好好,肯定不是得 他一开始说header有问题,不妨抓包看看,果然有东西 访问看看,乱码修复一下,在之前的博客到过 <img src…...
下载已编译的 OpenCV 包在 Visual Studio 下实现快速配置
自己编译 OpenCV 挺麻烦的,配置需要耗费很长时间,编译也需要很长时间,而且无法保证能全部编译通过。利用 OpenCV 官网提供的已编译的 OpenCV 库可以节省很多时间。下面介绍安装配置方法。 1. OpenCV 官网 地址是:https://opencv…...

【Linux系统学习】3.Linux用户和权限
Linux用户和权限 1.认知root用户 1.1 root用户(超级管理员) 无论是Windows、MacOS、Linux均采用多用户的管理模式进行权限管理。 在Linux系统中,拥有最大权限的账户名为:root(超级管理员) 而在前期&#…...

视频美颜SDK开发指南:从入门到精通的技术实践
美颜SDK是一种强大的工具,它不仅仅可以让用户在实时视频中获得光滑的肌肤和自然的妆容,从简单的滤镜到复杂的人脸识别,美颜SDK涵盖了广泛的技术领域。 一、美颜SDK的基本原理 美颜SDK包括图像处理、人脸检测和识别、滤镜应用等方面。掌握这些…...

Electron基本介绍
Electron基本介绍 Electron 官方网站:https://www.electronjs.org/zh/ Electron安装方法:npm install electron -g 全局安装 Electron简介:Electron提供了丰富的本地(操作系统)API,使你能够使用纯JavaScr…...

使用网关过滤器,根据业务规则实现微服务动态路由
文章目录 业务场景拦截器实现Spring Cloud Gateway介绍 业务场景 我们服务使用Spring Cloud微服务架构,使用Spring Cloud Gateway 作为网关,使用 Spring Cloud OpenFeign 作为服务间通信方式作为网关,主要作用是鉴权与路由转发。大多数应用场…...

PKI - 03 密钥管理(如何进行安全的公钥交换)
文章目录 Pre密钥管理面临的挑战安全密钥管理的几种方式手动密钥交换与确认受信任的介绍 Pre PKI - 02 对称与非对称密钥算法 密钥管理面临的挑战 密钥管理面临的挑战主要包括以下几点: 安全的公钥交换:在使用基于非对称密钥算法的服务之前,…...
Bee+SpringBoot稳定的Sharding、Mongodb ORM功能(同步 Maven)
Hibernate/MyBatis plus Sharding JDBC Jpa Spring data GraphQL App ORM (Android, 鸿蒙) Bee 小巧玲珑!仅 860K, 还不到 1M, 但却是功能强大! V2.2 (2024春节・LTS 版) 1.Javabean 实体支持继承 (配置 bee.osql.openEntityCanExtendtrue) 2. 增强批…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
