【LeetCode每日一题】525连续数组 303区域和检索(前缀和的基本概念和3个简单案例)
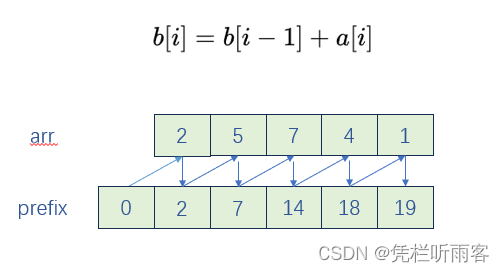
前缀和
// 构造prefix
let prefix = [0]
arr.forEach(num => {prefix.push(prefix.at(-1) + num);
})如果想要计算某个区间 i 到 j 这个子数组的和时,可以根据 prefix[j+1] - prefix[i] 获得。
例题1:303.区域和检索 - 数组不可变
给定一个整数数组 nums,处理以下类型的多个查询:
- 计算索引
left和right(包含left和right)之间的nums元素的 和 ,其中left <= right
实现 NumArray 类:
NumArray(int[] nums)使用数组nums初始化对象int sumRange(int i, int j)返回数组nums中索引left和right之间的元素的 总和 ,包含left和right两点(也就是nums[left] + nums[left + 1] + ... + nums[right])
/*** @param {number[]} nums*/
var NumArray = function(nums) {this.sum = new Array(nums.length+1).fill(0);for(let i =0;i<n;i++){this.sum[i+1] = this.sum[i]+nums[i]}
};/** * @param {number} left * @param {number} right* @return {number}*/
NumArray.prototype.sumRange = function(left, right) {return this.sum[right+1 ]-this.sum[left];
};/*** Your NumArray object will be instantiated and called as such:* var obj = new NumArray(nums)* var param_1 = obj.sumRange(left,right)*/
例题2
数组water表示一排瓶子的水位高度。小明往这些瓶子内浇水,1次操作可以使1个瓶子的水位增加1。给定一个整数cnt,表示小明想通过浇水获得cnt个水位高度一致的瓶子。求最少需要浇水多少次?
比如:[1,2,3,4,100] ,cnt = 4,想要获得4个,最少需要浇水
(4-1) + (4-2)+(4-3)+(4-4)
⇒ 4 * 4 - (1+2+3+4)
⇒ 4* cnt - cnt个元素的区域和。
计算操作次数的公式为:water[i] * cnt - (preSum[i + 1] - preSum[i - cnt + 1])。
这个公式表示将当前位置到第cnt个瓶子的水位高度都调整为当前位置的水位高度所需的总操作次数。
下面是修改后的代码实现:
const MinOperations = (water, cnt) => {water.sort((a, b) => b - a); // 按照从大到小排序let preSum = [0];water.forEach((element) => {preSum.push(preSum[preSum.length - 1] + element);});let res = Infinity;for (let i = cnt - 1; i < water.length; i++) {let temp = water[i] * cnt - (preSum[i + 1] - preSum[i - cnt + 1]);if (temp < res) res = temp;if (res === 0) break; // 如果res的值已经为0,表示不需要再进行更多操作,可以跳出循环}return res;
};console.log(MinOperations([7, 1, 9, 10], 3));
console.log(MinOperations([5, 3, 5, 10], 2));
在给定的示例中,第一个输入数组为[7, 1, 9, 10],表示瓶子的水位高度,cnt为3。运行代码后,输出为2,表示最少需要浇水2次才能使3个瓶子的水位高度一致。第二个输入数组为[5, 3, 5, 10],cnt为2。运行代码后,输出为3,表示最少需要浇水3次才能使2个瓶子的水位高度一致。
例题3:525. 连续数组
给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组,并返回该子数组的长度。
妈的 连题目都没有读懂!本来看成是找到两个连续子数组,两个连续子数组的 0 1 个数分别相同,我说怎么看着如此复杂。
题目转换:
找到一个连续子数组,其中0和1 的数量是一致的,求最大的连续子数组的长度。
解题过程
暴力:
遍历所有连续子数组的0和1 的个数,如果相同,则维护这个连续子数组的最大长度。
巧妙的转换:
相同数量的0和1 ⇒ 将 0 → -1 ⇒ 连续子数组和 为 0
如果想要求子数组的元素和 ⇒ 计算数组的前缀和。
prefixSum[i] : [0…i] 的前缀和,元素的累加。
[i…k] 的元素累加和 = prefixSum[k]-prefixSum[i-1]
所以:相同数量的0和1 ⇒ 将 0 → -1 ⇒ 连续子数组和 为 0 ⇒ prefixSum[k]-prefixSum[i] = 0 长度为 i- k ⇒ 当出现前缀和相同时维护一个最大的长度。
思路1:(x)
- 维护一个prefixSum表。遍历nums
- 用两个for循环,遍历所有子数组。
思路2:
- 用一个map记录前缀和和第一次出现的位置。key⇒value 的形式。
- map.has 意味着出现了前缀和一致的情况,则维护最大长度。
/*** @param {number[]} nums* @return {number}*/
var findMaxLength = function(nums) {let max = 0;// 如果连续子数组索引从0开始,则是priefix-prefix[-1],因此要提前保存-1,但是很难想到。const map = new Map();map.set(0,-1)let sum= 0;for (let i = 0; i < nums.length; i++) {if (nums[i] === 0) {sum--; // 遇到0 则-1,相当于把0元素简化为-1} else {sum++;}if (map.has(sum)) {// 出现了相同的前缀和,相减=0,说明这个区域和为0,说明0和1的个数相同max = Math.max(max, i - map.get(sum));// 不用更新sum的索引,因为要求的是最大的} else {map.set(sum, i);}}return max;
};思路3:
最长的连续子数组是以index = 0 为开头的特殊情况,要么使用思路二,在map里添加 index = -1 的情况。
要么使用思路三:sum = 0 的情况,sum是从index = 0 开始算的,相当于算的就是每个以index = 0 为开头的连续子数组的和。
/*** @param {number[]} nums* @return {number}*/
var findMaxLength = function(nums) {let max = 0;const map = new Map();let sum = 0;for (let i = 0; i < nums.length; i++) {if (nums[i] === 0) {sum --;} else {sum ++;}if(sum === 0){max = Math.max(max,i+1)}else if (map.has(sum)) {max = Math.max(max, i - map.get(sum));} else {map.set(sum , i);}}return max;
};相关文章:

【LeetCode每日一题】525连续数组 303区域和检索(前缀和的基本概念和3个简单案例)
前缀和 // 构造prefix let prefix [0] arr.forEach(num > {prefix.push(prefix.at(-1) num); })如果想要计算某个区间 i 到 j 这个子数组的和时,可以根据 prefix[j1] - prefix[i] 获得。 例题1:303.区域和检索 - 数组不可变 给定一个整数数组 num…...
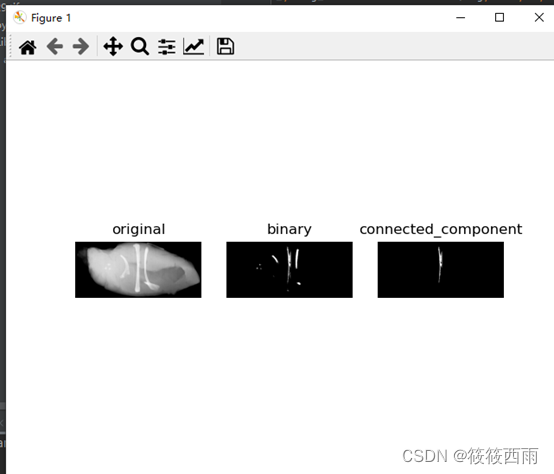
形态学算法应用之连通分量提取的python实现——图像处理
原理 连通分量提取是图像处理和计算机视觉中的一项基本任务,旨在识别图像中所有连通区域,并将它们作为独立对象处理。在二值图像中,连通分量通常指的是所有连接在一起的前景像素集合。这里的“连接”可以根据四连通或八连通的邻接关系来定义…...

Kafka系列之:Kafka集群同时设置基于时间和日志大小两种方式保存Topic的数据
Kafka系列之:Kafka集群同时设置基于时间和日志大小两种方式保存Topic的数据 一、基于日志大小二、基于时间大小三、参数设置四、设置命令一、基于日志大小 "log.retention.bytes"是Apache Kafka中的一项配置参数,用于指定每个日志段文件的最大大小。当日志段文件的…...

pytest+allure批量执行测试用例
在 Pytest 中,可以使用装饰器 `@pytest.fixture` 来定义用例级别的前置和后置操作。下面是一个示例代码,演示了如何使用 Pytest 的前置和后置操作: ```python import pytest @pytest.fixture(scope="function") def setup_function(): print("Setup fu…...
SpringBoot和SpringMVC
目录 一、springboot项目 (1)创建springboot项目 (2)目录介绍 (3)项目启动 (4)运行一个程序 (5)通过其他方式创建和运行springboot项目 二、SpringMVC…...
免费搭建幻兽帕鲁服务器,白嫖阿里云游戏服务器
阿里云幻兽帕鲁服务器免费搭建方案,先在阿里云高校计划「云工开物」活动领取学生专享300元无门槛代金券,幻兽帕鲁专用服务器4核16G配置26元1个月、149元半年,直接使用这个无门槛300元代金券抵扣即可免费搭建幻兽帕鲁服务器。阿里云服务器网al…...
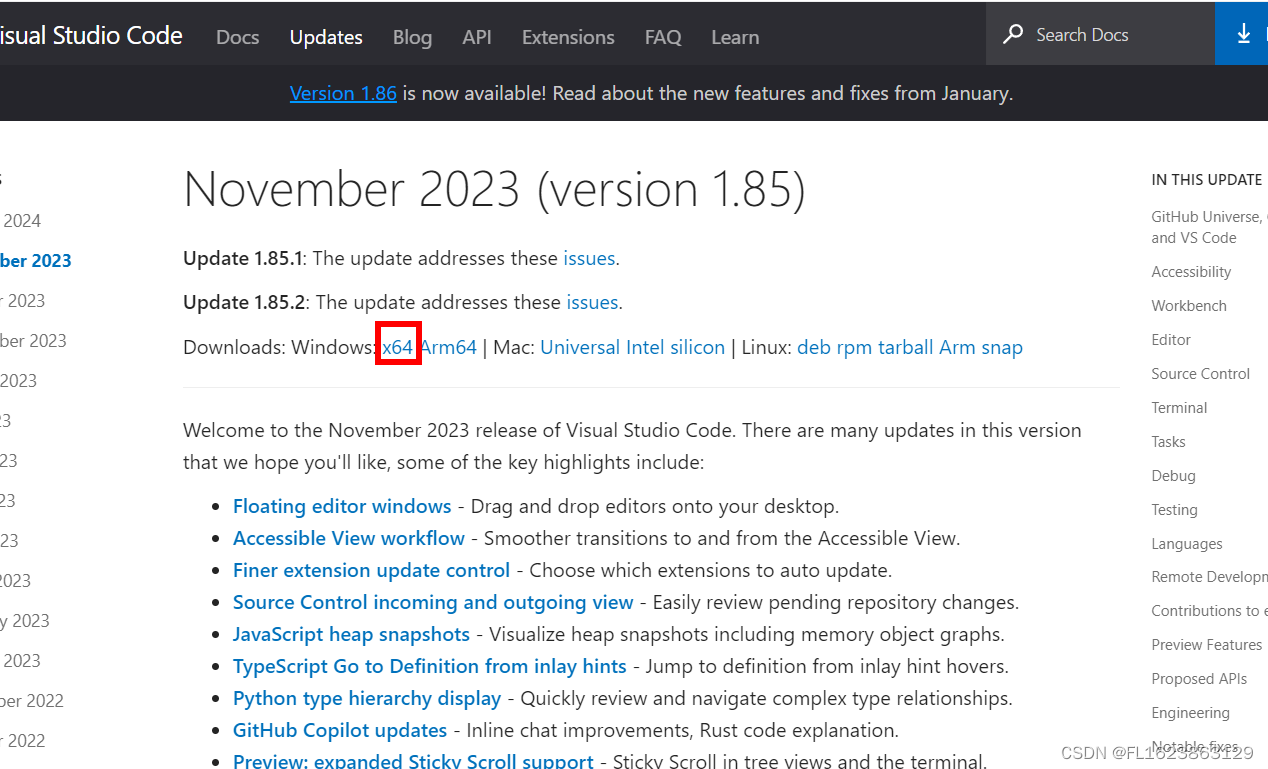
[技术杂谈]如何下载vscode历史版本
网站模板: https://code.visualstudio.com/updates/v1_85 如果你想下载1.84系列可以访问https://code.visualstudio.com/updates/v1_84 然后看到: 选择对应版本下载即可,我是windows x64系统选择x64即可开始下载...

nginx slice模块的使用和源码分析
文章目录 1. 为什么需要ngx_http_slice_module2. 配置指令3. 加载模块4. 源码分析4.1 指令分析4.2 模块初始化4.3 slice模块的上下文4.2 $slice_range字段值获取4.3 http header过滤处理4.4 http body过滤处理5 测试和验证 1. 为什么需要ngx_http_slice_module 顾名思义&#…...

AI应用开发-python实现redis数据存储
AI应用开发相关目录 本专栏包括AI应用开发相关内容分享,包括不限于AI算法部署实施细节、AI应用后端分析服务相关概念及开发技巧、AI应用后端应用服务相关概念及开发技巧、AI应用前端实现路径及开发技巧 适用于具备一定算法及Python使用基础的人群 AI应用开发流程概…...

2024年Java架构篇之设计模式
2024年Java实战面试题_java 5 年 面试-CSDN博客 1、单例模式...

搭建macOS开发环境-1:准备工作
请记住: 最重要的准备工作永远是:备份数据 !!! 通过图形界面检查 Mac 的 CPU 类型: 在搭载 Apple 芯片的 Mac 电脑上,“关于本机”会显示一个标有“芯片”的项目并跟有相应芯片的名称: 通过命令行检查Mac的CPU类型 …...

【Makefile语法 02】Makefile语法基础
目录 一、Makefile概述 二、Makefile变量 三、Makefile符号 一、Makefile格式 1. 基本格式: targets : prerequisties [tab键]command target:目标文件,可以是 OjectFile,也可以是执行文件,还可以是一个标签&…...

如何写一个其他人可以使用的GitHub Action
前言 在GitHub中,你肯定会使用GitHub Actions自动部署一个项目到GitHub Page上,在这个过程中总要使用workflows工作流,并在其中使用action,在这个使用的过程中,总会好奇怎么去写一个action呢,所以ÿ…...

排序算法的时间复杂度存在下界问题
对于几种常用的排序算法,无论是归并排序、快速排序、以及更加常见的冒泡排序等,这些排序算法的时间复杂度都是大于等于O(n*lg(n))的,而这些排序算法存在一个共同的行为,那就是这些算法在对元素进行排序的时候,都会进行…...
)
详解洛谷P2016 战略游戏/BZOJ0495. 树的最小点覆盖之战略游戏(贪心/树形DP)
Description Bob喜欢玩电脑游戏,特别是战略游戏。但是他经常无法找到快速玩过游戏的办法。现在他有个问题。 他要建立一个古城堡,城堡中的路形成一棵树。他要在这棵树的结点上放置最少数目的士兵,使得这些士兵能了望到所有的路。 注意&…...

解决The Tomcat connector configured to listen on port 8080 failed to start
问题 启动javar报错,提示如下 Description: The Tomcat connector configured to listen on port 8080 failed to start. The port may already be in use or the connector may be misconfigured. Action: Verify the connector’s configuration, identify a…...
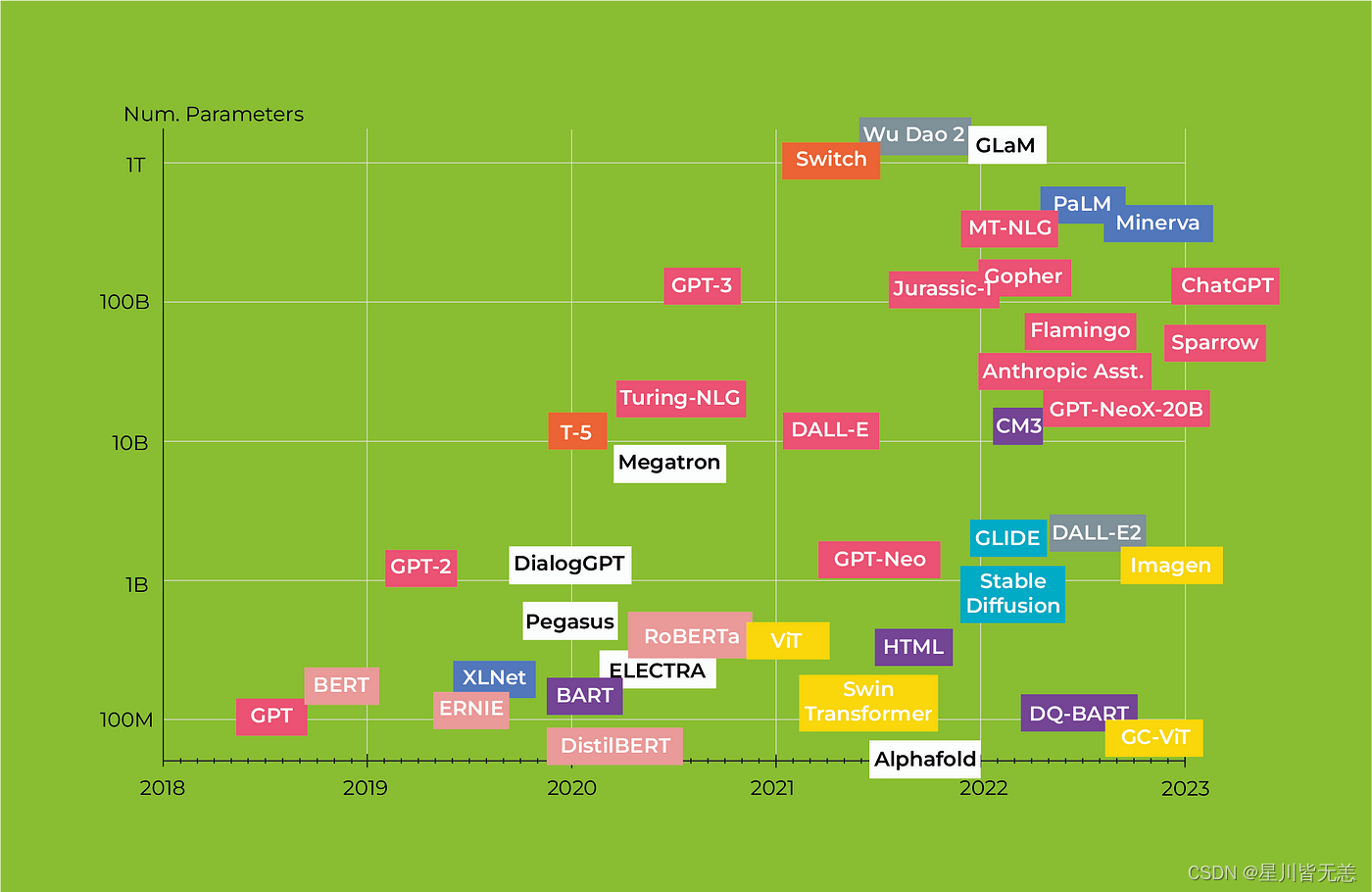
深度学习自然语言处理(NLP)模型BERT:从理论到Pytorch实战
文章目录 深度学习自然语言处理(NLP)模型BERT:从理论到Pytorch实战一、引言传统NLP技术概览规则和模式匹配基于统计的方法词嵌入和分布式表示循环神经网络(RNN)与长短时记忆网络(LSTM)Transform…...
C语言的循环结构
目录 前言 1.三种循环语句 1.while循环 2.for循环 2.1缺少表达式的情况 3.do while循环 2.break语句和continue语句 2.1在while循环中 2.2在for循环中 2.3在do while 循环中 3.循环的嵌套 4.go to语句 前言 C语⾔是结构化的程序设计语⾔,这⾥的结构指的是…...
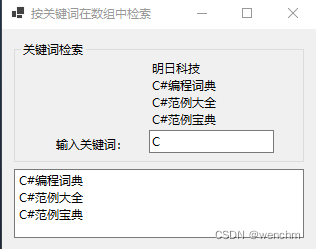
C#用Array类的FindAll方法和List<T>类的Add方法按关键词在数组中检索元素并输出
目录 一、使用的方法 1. Array.FindAll(T[], Predicate) 方法 (1)定义 (2)示例 2.List类的常用方法 (1)List.Add(T) 方法 (2)List.RemoveAt(Int32) 方法 (3&…...
附完整源码】)
【前后端接口AES+RSA混合加解密详解(vue+SpringBoot)附完整源码】
前后端接口AES+RSA混合加解密详解(vue+SpringBoot) 前后端接口AES+RSA混合加解密一、AES加密原理和为什么不使用AES加密二、RSA加密原理和为什么不使用rsa加密三、AES和RSA混合加密的原理四、代码样例前端1. 请求增加加密标识2. 前端加密工具类3.前端axios请求统一封装,和返…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
