详解洛谷P2016 战略游戏/BZOJ0495. 树的最小点覆盖之战略游戏(贪心/树形DP)
Description
Bob喜欢玩电脑游戏,特别是战略游戏。但是他经常无法找到快速玩过游戏的办法。现在他有个问题。
他要建立一个古城堡,城堡中的路形成一棵树。他要在这棵树的结点上放置最少数目的士兵,使得这些士兵能了望到所有的路。
注意,某个士兵在一个结点上时,与该结点相连的所有边将都可以被了望到。
请你编一程序,给定一树,帮Bob计算出他需要放置最少的士兵.
Format
Input
第一行 N,表示树中结点的数目。
第二行至第N+1行,每行描述每个结点信息,依次为:该结点标号i,k(后面有k条边与结点I相连)。
接下来k个数,分别是每条边的另一个结点标号r1,r2,…,rk。
对于一个n(0<n<=1500)个结点的树,结点标号在0到n-1之间,在输入数据中每条边只出现一次。
Output
输出文件仅包含一个数,为所求的最少的士兵数目。
Samples
输入数据 1
4
0 1 1
1 2 2 3
2 0
3 0
Copy
输出数据 1
1
Copy
Hint 答案为1(只要一个士兵在结点1上)。
思路1:树形DP
可以先看看详解洛谷P1352 没有上司的舞会(树形DP经典例题)-CSDN博客
定义状态dp[x][0/1]表示x这个节点不放/放士兵
根据题意,如果当前节点不放置士兵,那么它的子节点必须全部放置士兵,因为要满足士兵可以看到所有的边
dp[x][0] += dp[son][1]
其中son是u的子节点
如果当前节点放置士兵,只要将dp[x][1]加上它的子节点选不选的最小值就行了(因为树形dp自下而上,上面的节点不需要考虑)
dp[x][1]+=min(dp[son][0],dp[son][1])
代码(树形DP)
#include <bits/stdc++.h>
#define int long long
using namespace std;
int n,u,v,dp[10001][2];
vector<int> vec[100001];
void dfs(int fa,int x)
{dp[x][1] = 1;for(int i = 0;i < vec[x].size();i++)if(vec[x][i] != fa){dfs(x,vec[x][i]);dp[x][0] += dp[vec[x][i]][1];dp[x][1] += min(dp[vec[x][i]][0],dp[vec[x][i]][1]);}
}
signed main()
{cin>>n;for(int i = 1;i <= n;i++){int p;cin>>p>>u;for(int j = 1;j <= u;j++){cin>>v;vec[p].push_back(v);vec[v].push_back(p);}}dfs(-1,0);cout<<min(dp[0][1],dp[0][0]);return 0;
}思路2:贪心
可以按照反方向的深度优先遍历序列来进行贪心。每检查一个结点,如果当前点和当前点的父节点都不属于顶点覆盖集合,则将父节点加入到顶点覆盖集合,并标记当前节点和其父节点都被覆盖.
虽然说着思路很简单,但是代码细节蛮多的,可以参考一下。
代码(贪心)
#include <bits/stdc++.h>
#define int long long
using namespace std;
int n,u,v,ans,fat[100001],cnt;
struct st
{int zhi,id;
}dp[100001];
bool vis[100001];
vector<int> vec[100001];
void dfs(int fa,int x,int dep)
{dp[++cnt] = {dep,x};fat[x] = fa;for(int i = 0;i < vec[x].size();i++)if(vec[x][i] != fa)dfs(x,vec[x][i],dep + 1);
}
bool cmp(st x,st y)
{return x.zhi > y.zhi;
}
signed main()
{cin>>n;for(int i = 1;i <= n;i++){int p;cin>>p>>u;for(int j = 1;j <= u;j++){cin>>v;vec[p].push_back(v);vec[v].push_back(p);}}vis[1501] = 1;dfs(1501,0,1);sort(dp + 1,1 + dp + n,cmp);for(int i = 1;i <= n;i++)if(vis[dp[i].id] == 0 && vis[fat[dp[i].id]] == 0){vis[fat[dp[i].id]] = 1;vis[dp[i].id] = 1;ans++;}cout<<ans;return 0;
}结语
如果这篇博客对您有帮助的话,请点赞收藏关注支持一下呗!(o゜▽゜)o☆
相关文章:
)
详解洛谷P2016 战略游戏/BZOJ0495. 树的最小点覆盖之战略游戏(贪心/树形DP)
Description Bob喜欢玩电脑游戏,特别是战略游戏。但是他经常无法找到快速玩过游戏的办法。现在他有个问题。 他要建立一个古城堡,城堡中的路形成一棵树。他要在这棵树的结点上放置最少数目的士兵,使得这些士兵能了望到所有的路。 注意&…...

解决The Tomcat connector configured to listen on port 8080 failed to start
问题 启动javar报错,提示如下 Description: The Tomcat connector configured to listen on port 8080 failed to start. The port may already be in use or the connector may be misconfigured. Action: Verify the connector’s configuration, identify a…...
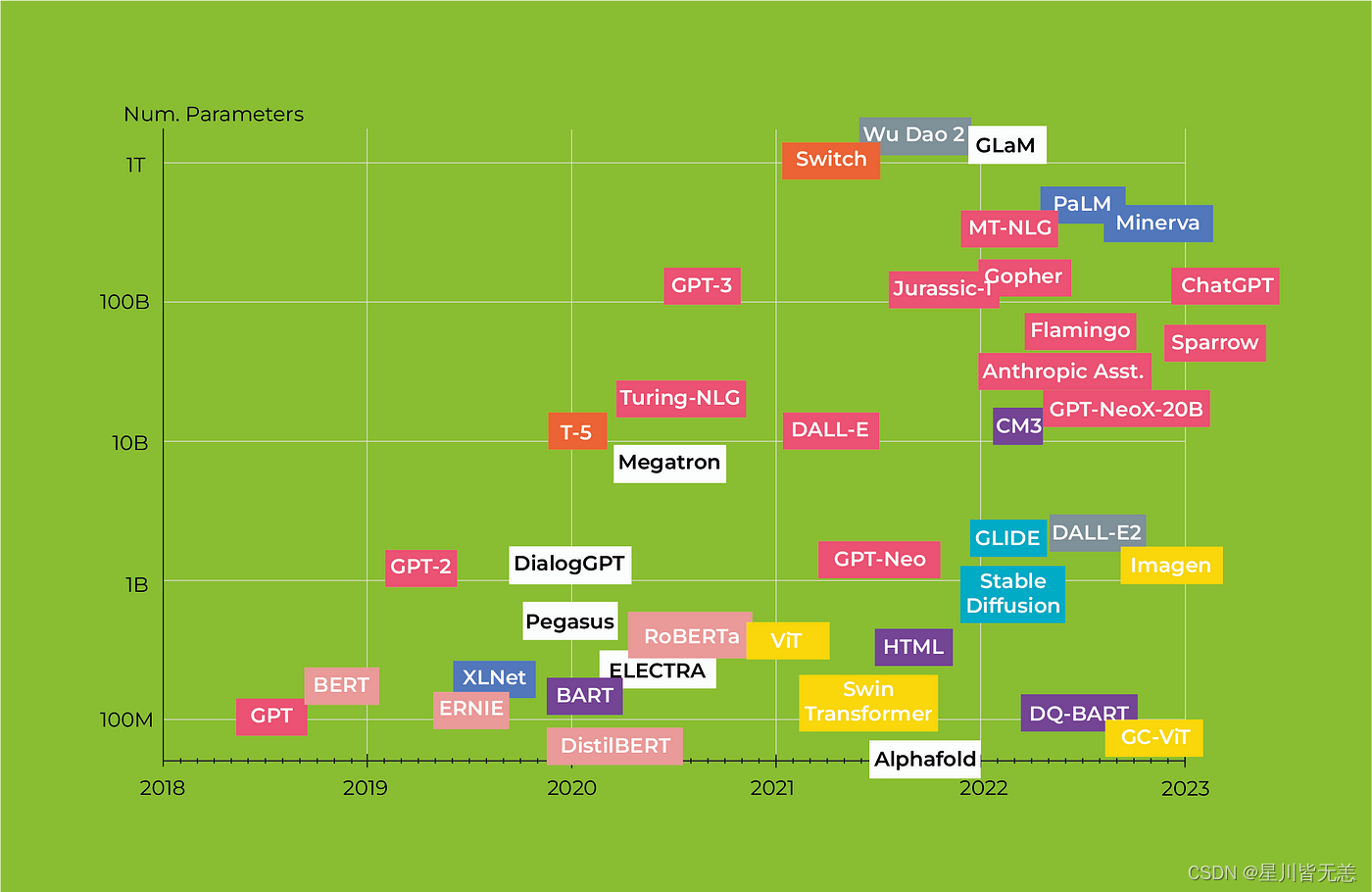
深度学习自然语言处理(NLP)模型BERT:从理论到Pytorch实战
文章目录 深度学习自然语言处理(NLP)模型BERT:从理论到Pytorch实战一、引言传统NLP技术概览规则和模式匹配基于统计的方法词嵌入和分布式表示循环神经网络(RNN)与长短时记忆网络(LSTM)Transform…...
C语言的循环结构
目录 前言 1.三种循环语句 1.while循环 2.for循环 2.1缺少表达式的情况 3.do while循环 2.break语句和continue语句 2.1在while循环中 2.2在for循环中 2.3在do while 循环中 3.循环的嵌套 4.go to语句 前言 C语⾔是结构化的程序设计语⾔,这⾥的结构指的是…...
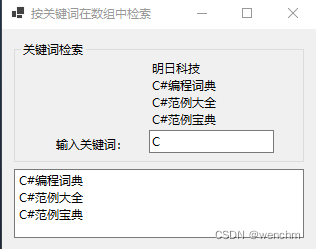
C#用Array类的FindAll方法和List<T>类的Add方法按关键词在数组中检索元素并输出
目录 一、使用的方法 1. Array.FindAll(T[], Predicate) 方法 (1)定义 (2)示例 2.List类的常用方法 (1)List.Add(T) 方法 (2)List.RemoveAt(Int32) 方法 (3&…...
附完整源码】)
【前后端接口AES+RSA混合加解密详解(vue+SpringBoot)附完整源码】
前后端接口AES+RSA混合加解密详解(vue+SpringBoot) 前后端接口AES+RSA混合加解密一、AES加密原理和为什么不使用AES加密二、RSA加密原理和为什么不使用rsa加密三、AES和RSA混合加密的原理四、代码样例前端1. 请求增加加密标识2. 前端加密工具类3.前端axios请求统一封装,和返…...
React环境配置
1.安装Node.js Node.js官网:https://nodejs.org/en/ 下载之后按默认选项安装好 重启电脑即可自动完成配置 2.安装React 国内使用 npm 速度很慢,可以使用淘宝定制的 cnpm (gzip 压缩支持) 命令行工具代替默认的 npm。 ①使用 winR 输入 cmd 打开终端 ②依…...

Pandas 数据处理-排序与排名的深度探索【第69篇—python:文本数据处理】
文章目录 Pandas 数据处理-排序与排名的深度探索1. sort_index方法2. sort_values方法3. rank方法4. 多列排序5. 排名方法的参数详解6. 处理重复值7. 对索引进行排名8. 多级索引排序与排名9. 更高级的排序自定义10. 性能优化技巧10.1 使用nsmallest和nlargest10.2 使用sort_val…...

第8节、双电机多段直线运动【51单片机+L298N步进电机系列教程】
↑↑↑点击上方【目录】,查看本系列全部文章 摘要:前面章节主要介绍了bresenham直线插值运动,本节内容介绍让两个电机完成连续的直线运动,目标是画一个正五角星 一、五角星图介绍 五角星总共10条直线,10个顶点。设定左下角为原点…...
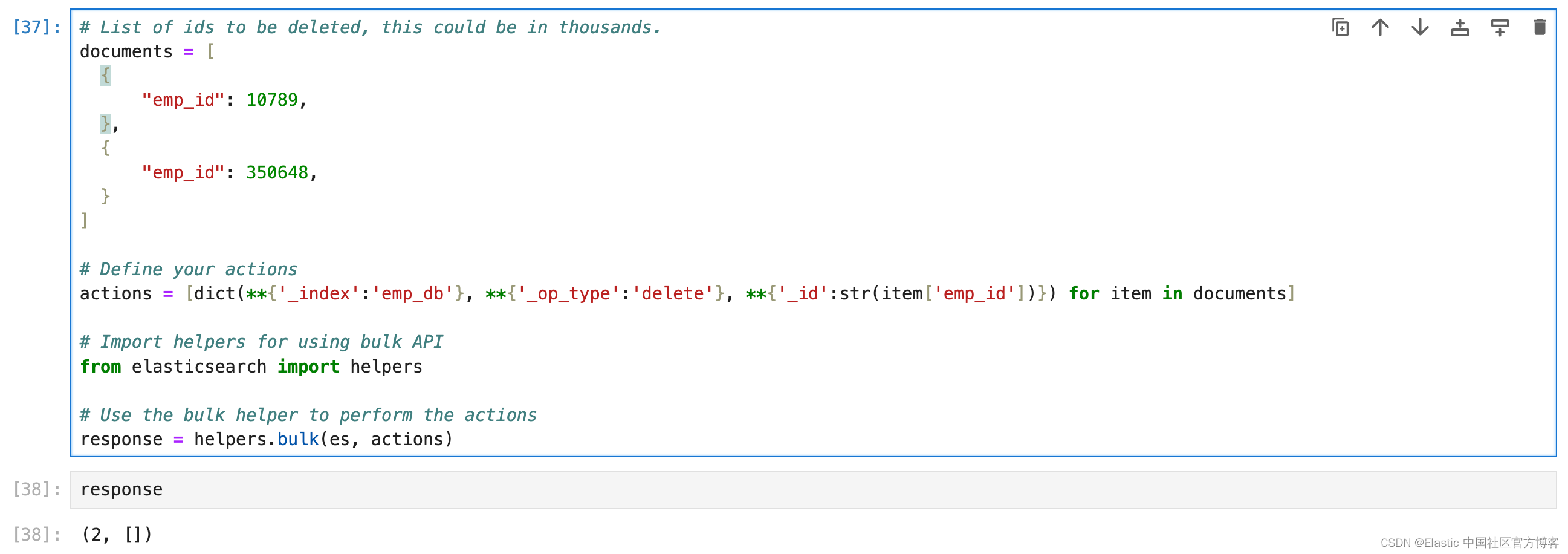
Elasticsearch:基本 CRUD 操作 - Python
在我之前的文章 “Elasticsearch:关于在 Python 中使用 Elasticsearch 你需要知道的一切 - 8.x”,我详细讲述了如何建立 Elasticsearch 的客户端连接。我们也详述了如何对数据的写入及一些基本操作。在今天的文章中,我们针对数据的 CRUD (cre…...
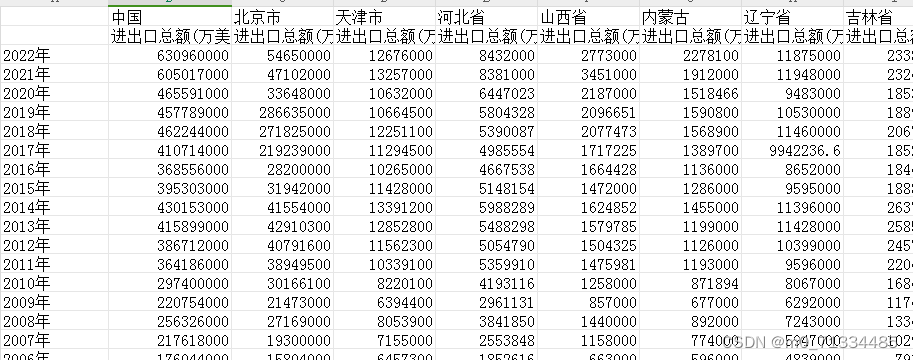
1992-2022年全国及31省对外开放度测算数据(含原始数据+计算结果)(无缺失)
1992-2022年全国及31省对外开放度测算数据(含原始数据计算结果)(无缺失) 1、时间:1992-2022年 2、来源:各省年鉴、国家统计局、统计公报、 3、指标:进出口总额(万美元)…...

JVM之GC垃圾回收
GC垃圾回收 如何判断对象可以回收 引用计数法 如果有对象引用计数加一,没有对象引用,计数减一,如果计数为零,则回收 但是如果存在循环引用,即A对象引用B对象,B对象引用A对象,会造成内存泄漏 可…...

自然语言学习nlp 六
https://www.bilibili.com/video/BV1UG411p7zv?p118 Delta Tuning,尤其是在自然语言处理(NLP)和机器学习领域中,通常指的是对预训练模型进行微调的一种策略。这种策略不是直接更新整个预训练模型的权重,而是仅针对模型…...

fpga 需要掌握哪些基础知识?
个人根据自己的一些心得总结一下fpga 需要掌握的基础知识,希望对你有帮助。 1、数电(必须掌握的基础),然后进阶学模电, 2、掌握HDL(verilog或VHDL)一般建议先学verilog,然后可以学…...

Qt未来市场洞察
跨平台开发:Qt作为一种跨平台的开发框架,具有良好的适应性和灵活性,未来将继续受到广泛应用。随着多设备和多平台应用的增加,Qt的前景在跨平台开发领域将更加广阔。 物联网应用:由于Qt对嵌入式系统和物联网应用的良好支…...

GPT-4模型中的token和Tokenization概念介绍
Token从字面意思上看是游戏代币,用在深度学习中的自然语言处理领域中时,代表着输入文字序列的“代币化”。那么海量语料中的文字序列,就可以转化为海量的代币,用来训练我们的模型。这样我们就能够理解“用于GPT-4训练的token数量大…...

宽字节注入漏洞原理以及修复方法
漏洞名称:宽字节注入 漏洞描述: 宽字节注入是相对于单字节注入而言的,该注入跟HTML页面编码无关,宽字节注入常见于mysql中,GB2312、GBK、GB18030、BIG5、Shift_JIS等这些都是常说的宽字节,实际上只有两字节。宽字节带来的安全问…...

【Linux】SystemV IPC
进程间通信 一、SystemV 共享内存1. 共享内存原理2. 系统调用接口(1)创建共享内存(2)形成 key(3)测试接口(4)关联进程(5)取消关联(6)释…...

iview 页面中判断溢出才使用Tooltip组件
使用方法 <TextTooltip :content"contentValue"></TextTooltip> 给Tooltip再包装一下 <template><Tooltip transfer :content"content" :theme"theme" :disabled"!showTooltip" :max-width"300" :p…...
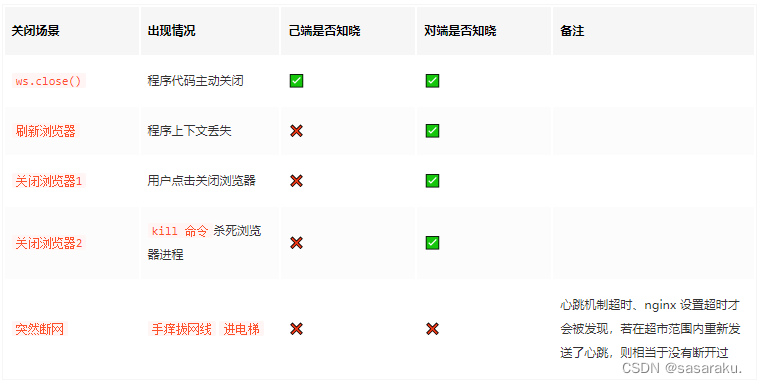
如何使用websocket
如何使用websocket 之前看到过一个面试题:吃饭点餐的小程序里,同一桌的用户点餐菜单如何做到的实时同步? 答案就是:使用websocket使数据变动时服务端实时推送消息给其他用户。 最近在我们自己的项目中我也遇到了类似问题…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
