1992-2022年全国及31省对外开放度测算数据（含原始数据+计算结果）（无缺失）
1992-2022年全国及31省对外开放度测算数据（含原始数据+计算结果）（无缺失）
1、时间：1992-2022年
2、来源：各省年鉴、国家统计局、统计公报、
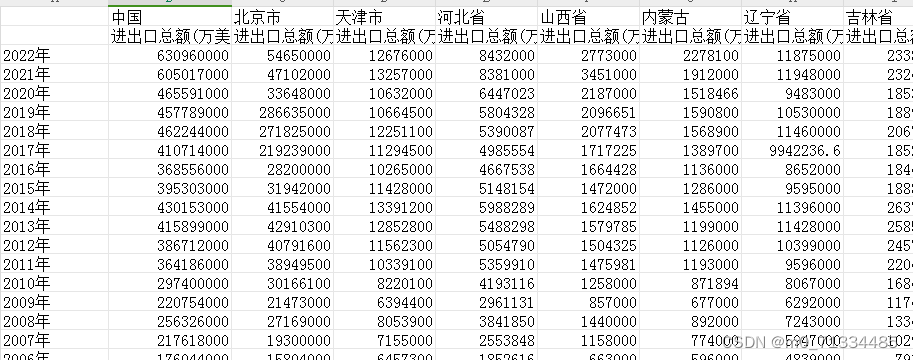
3、指标：进出口总额（万美元）、进出口总额（亿元）、汇率（年平均价）、国内生产总值（亿元）、对外开放度
4、范围：全国及31省
5、计算说明：对外开放度=进出口总额/国内生产总值
6、缺失情况：无缺失
7、指标解释;
对外开放度是指一个国家或地区经济对外开放的程度，具体表现为市场的开放程度。
开放度即为一国经济的对外开放程序，它有名义开放度与实际开放度之分，是衡量一国经济对外开放规模和水平的重要指标。
提高实际开放度应当成为我国改革开放的一个重要目标，对我国对外开放政策的制定与实施具指导作用。
8、下载链接：
1992-2022年全国及31省对外开放度测算数据含原始数据和计算过程
https://download.csdn.net/download/m0_71334485/88804888
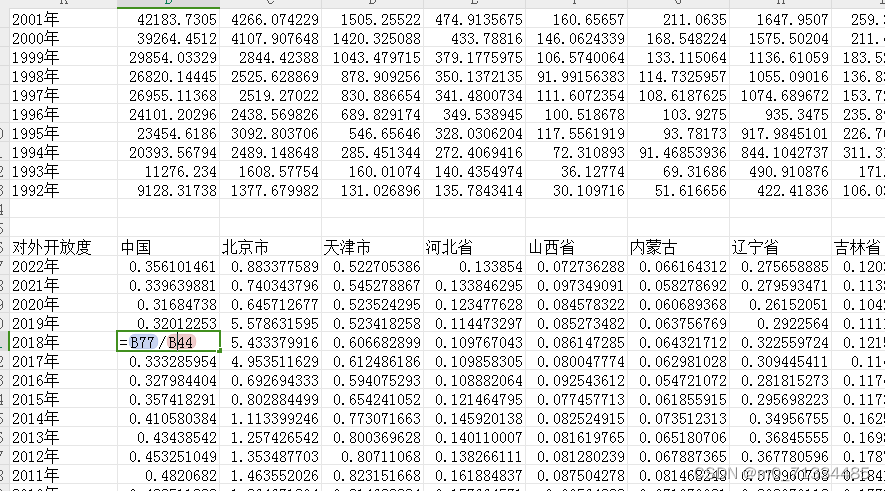
相关文章：
1992-2022年全国及31省对外开放度测算数据（含原始数据+计算结果）（无缺失）
1992-2022年全国及31省对外开放度测算数据（含原始数据计算结果）（无缺失） 1、时间：1992-2022年 2、来源：各省年鉴、国家统计局、统计公报、 3、指标：进出口总额（万美元）…...
JVM之GC垃圾回收
GC垃圾回收 如何判断对象可以回收 引用计数法 如果有对象引用计数加一，没有对象引用，计数减一，如果计数为零，则回收 但是如果存在循环引用，即A对象引用B对象，B对象引用A对象，会造成内存泄漏 可…...
自然语言学习nlp 六
https://www.bilibili.com/video/BV1UG411p7zv?p118 Delta Tuning，尤其是在自然语言处理（NLP）和机器学习领域中，通常指的是对预训练模型进行微调的一种策略。这种策略不是直接更新整个预训练模型的权重，而是仅针对模型…...
fpga 需要掌握哪些基础知识？
个人根据自己的一些心得总结一下fpga 需要掌握的基础知识，希望对你有帮助。 1、数电（必须掌握的基础），然后进阶学模电， 2、掌握HDL（verilog或VHDL）一般建议先学verilog，然后可以学…...
Qt未来市场洞察
跨平台开发：Qt作为一种跨平台的开发框架，具有良好的适应性和灵活性，未来将继续受到广泛应用。随着多设备和多平台应用的增加，Qt的前景在跨平台开发领域将更加广阔。 物联网应用：由于Qt对嵌入式系统和物联网应用的良好支…...
GPT-4模型中的token和Tokenization概念介绍
Token从字面意思上看是游戏代币，用在深度学习中的自然语言处理领域中时，代表着输入文字序列的“代币化”。那么海量语料中的文字序列，就可以转化为海量的代币，用来训练我们的模型。这样我们就能够理解“用于GPT-4训练的token数量大…...
宽字节注入漏洞原理以及修复方法
漏洞名称:宽字节注入 漏洞描述: 宽字节注入是相对于单字节注入而言的，该注入跟HTML页面编码无关，宽字节注入常见于mysql中，GB2312、GBK、GB18030、BIG5、Shift_JIS等这些都是常说的宽字节，实际上只有两字节。宽字节带来的安全问…...
【Linux】SystemV IPC
进程间通信 一、SystemV 共享内存1. 共享内存原理2. 系统调用接口（1）创建共享内存（2）形成 key（3）测试接口（4）关联进程（5）取消关联（6）释…...
iview 页面中判断溢出才使用Tooltip组件
使用方法 <TextTooltip :content"contentValue"></TextTooltip> 给Tooltip再包装一下 <template><Tooltip transfer :content"content" :theme"theme" :disabled"!showTooltip" :max-width"300" :p…...
如何使用websocket
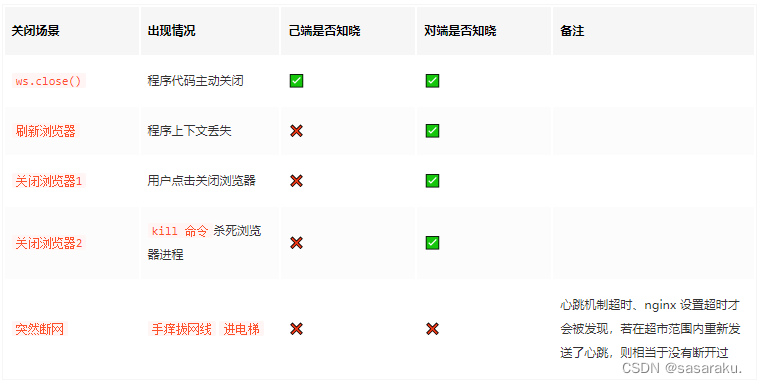
如何使用websocket 之前看到过一个面试题：吃饭点餐的小程序里，同一桌的用户点餐菜单如何做到的实时同步？ 答案就是：使用websocket使数据变动时服务端实时推送消息给其他用户。 最近在我们自己的项目中我也遇到了类似问题…...
C++ 调用lua 脚本
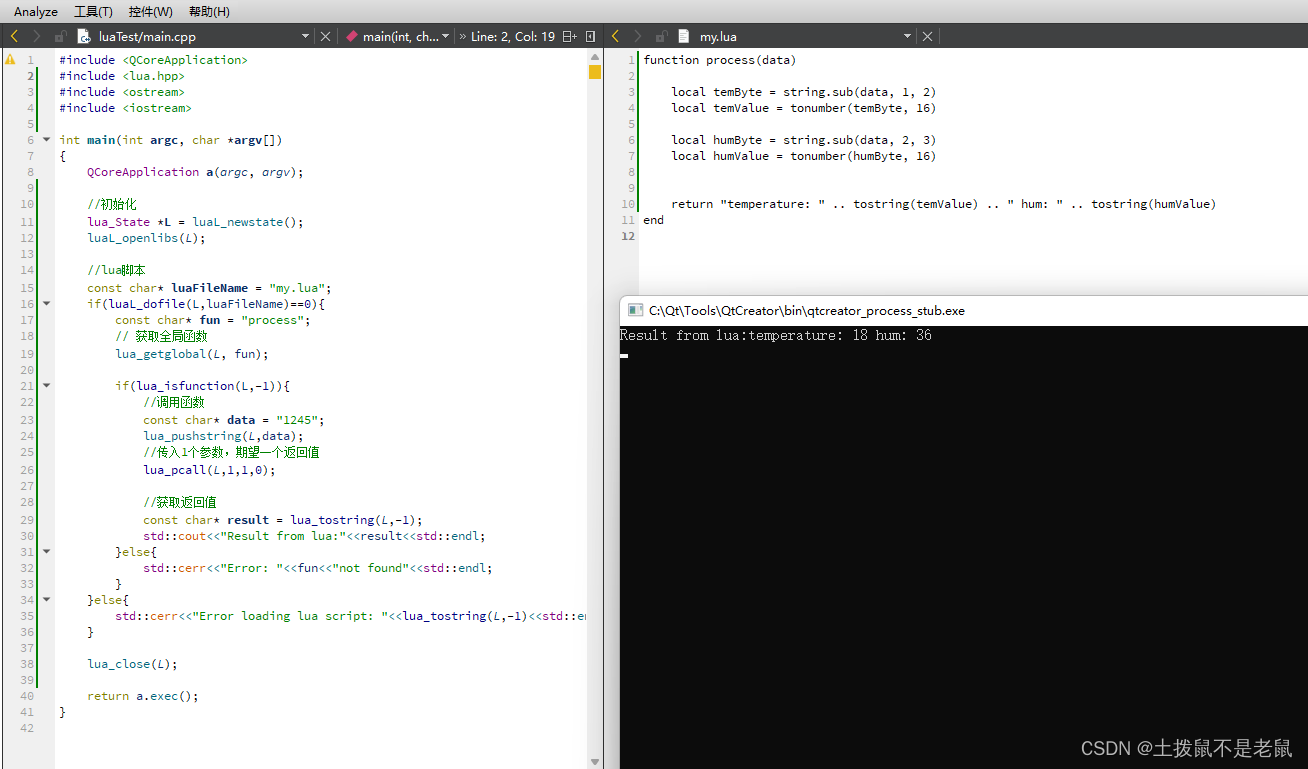
需求： 使用Qt/C 调用 lua 脚本 扩展原有功能。 步骤： 1，工程中引入 头文件，库文件。lua二进制下载地址（Lua Binaries） 2， 调用脚本内函数。 这里调用lua 脚本中的process函数，并…...
Centos 内存和硬盘占用情况以及top作用
目录 只查看内存使用情况： 内存使用排序取前5个： 硬盘占用情况 定位占用空间最大目录 top查看cpu及内存使用信息 前言-与正文无关 生活远不止眼前的苦劳与奔波，它还充满了无数值得我们去体验和珍惜的美好事物。在这个快节奏的世界中&…...
【数据结构】堆（创建，调整，插入，删除，运用）
目录 堆的概念： 堆的性质： 堆的存储方式： 堆的创建 ： 堆的调整： 向下调整： 向上调整： 堆的创建： 建堆的时间复杂度： 向下调整： 向上调整ÿ…...
v-if 和v-for的联合规则及示例
第073个 查看专栏目录: VUE ------ element UI 专栏目标 在vue和element UI联合技术栈的操控下，本专栏提供行之有效的源代码示例和信息点介绍，做到灵活运用。 提供vue2的一些基本操作：安装、引用，模板使用，computed&a…...
各互联网企业测绘资质调研
公司子公司产品产品介绍资质获得资质时间阿里巴巴高德高德地图作为阿里的全资子公司，中国领先的数字地图内容、导航和位置服务解决方案提供商，互联网地图行业龙头，2021年4月高德实现全月平均日活跃用户数超过1亿的重要里程碑，稳居…...
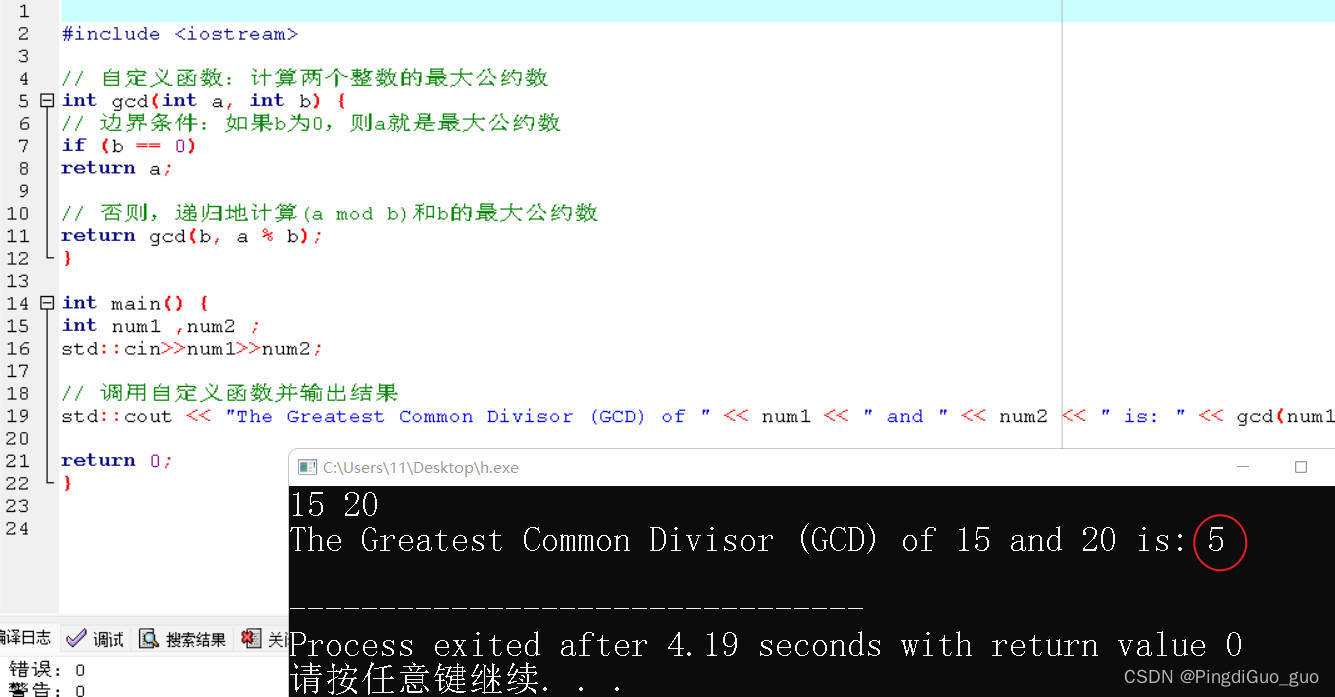
C++自定义函数详解
个人主页：PingdiGuo_guo 收录专栏：C干货专栏 铁汁们新年好呀，今天我们来了解自定义函数。 文章目录 1.数学中的函数 2.什么是自定义函数 3.自定义函数如何使用？ 4.值传递和引用传递（形参和实参区分） …...
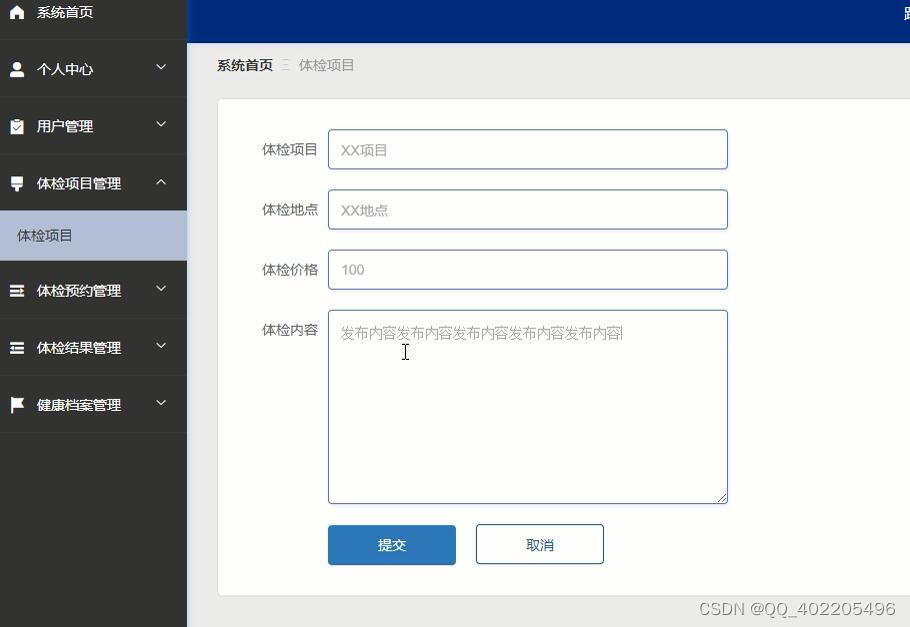
flask+vue+python跨区通勤人员健康体检预约管理系统
跨区通勤人员健康管理系统设计的目的是为用户提供体检项目等功能。 与其它应用程序相比，跨区通勤人员健康的设计主要面向于跨区通勤人员，旨在为管理员和用户提供一个跨区通勤人员健康管理系统。用户可以通过系统及时查看体检预约等。 跨区通勤人员健康管…...
Spring Boot动态加载Jar包与动态配置技术探究
Spring Boot动态加载Jar包与动态配置技术探究 1. 引言 在当今快节奏的软件开发领域，高效的开发框架是保持竞争力的关键。Spring Boot作为一款快速开发框架，以其简化配置、内嵌Web服务器、强大的开发工具等特性，成为众多开发者的首选。其背后…...
Lua metatable metamethod
示例代码 《programming in lua》里有一个案例很详细，就是写一个集合类的table，其负责筛选出table中不重复的元素并组合成一个新的table。本人按照自己的方式默写了一次，结果发现大差不差，代码如下： Set {} --集合--…...
HCIA-HarmonyOS设备开发认证V2.0-3.2.轻量系统内核基础-任务管理
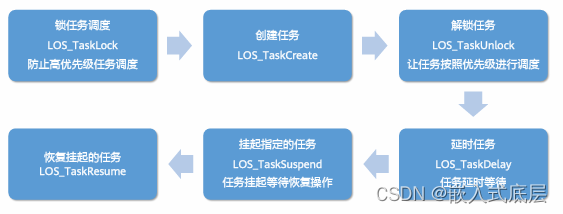
目录 一、任务管理1.1、任务状态1.2、任务基本概念1.3、任务管理使用说明1.4、任务开发流程1.5、任务管理接口 一、任务管理 从系统角度看，任务是竞争系统资源的最小运行单元。任务可以使用或等待CPU、使用内存空间等系统资源，并独立于其它任务运行。 O…...
【大模型RAG】拍照搜题技术架构速览：三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道（多模态 OCR → 语义检索 → 答案渲染）、两级检索（倒排 BM25 向量 HNSW）并以大语言模型兜底”的整体框架： 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后，分别用…...
内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤： 1）请求大小调整：首先，malloc 需要调整用户请求的大小，以适应内部数据结构（例如，可能需要存储额外的元数据）。通常，这包括对齐调整，确保分配的内存地址满足特定硬件要求（如对齐到8字节或16字节边界）。 2）空闲…...
大话软工笔记—需求分析概述
需求分析，就是要对需求调研收集到的资料信息逐个地进行拆分、研究，从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要，后续设计的依据主要来自于需求分析的成果，包括: 项目的目的…...
脑机新手指南（八）：OpenBCI_GUI：从环境搭建到数据可视化（下）
一、数据处理与分析实战 （一）实时滤波与参数调整 基础滤波操作 60Hz 工频滤波：勾选界面右侧 “60Hz” 复选框，可有效抑制电网干扰（适用于北美地区，欧洲用户可调整为 50Hz）。 平滑处理&…...
VB.net复制Ntag213卡写入UID
本示例使用的发卡器：https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...
-----深度优先搜索（DFS）实现)
c++ 面试题(1)-----深度优先搜索（DFS）实现
操作系统：ubuntu22.04 IDE:Visual Studio Code 编程语言：C11 题目描述 地上有一个 m 行 n 列的方格，从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子，但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...
【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件（System Property Definition File），用于声明和管理 Bluetooth 模块相…...
零基础设计模式——行为型模式 - 责任链模式
第四部分：行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习！行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想：使多个对象都有机会处…...
NFT模式：数字资产确权与链游经济系统构建
NFT模式：数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新：构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议：基于LayerZero协议实现以太坊、Solana等公链资产互通，通过零知…...
全面解析各类VPN技术：GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec？ IPsec VPN 5.1 IPsec传输模式（Transport Mode） 5.2 IPsec隧道模式（Tunne…...