高斯消去法 | LU分解 | PA=LU分解(MatLab)
一、问题描述
利用高斯消去法,LU 分解及PA=LU 分解求解非线性方程组。
二、实验目的
掌握高斯消去法、LU 分解、PA=LU 分解的算法原理;编写代码实现利用高斯消去法、LU 分解、PA=LU 分解来求解线性方程组。
三、实验内容及要求
1. 利用顺序高斯消去法求解如下方程组。
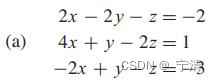
(注意将顺序高斯消去法封装为一个函数,函数名Gauss,该函数对应的文件同样命名为Gauss)。
function x = Gauss(A, b)n = length(b);for k = 1:n-1for i = k+1:nfactor = A(i,k) / A(k,k);A(i,k+1:n) = A(i,k+1:n) - factor * A(k,k+1:n);b(i) = b(i) - factor * b(k);endendx = zeros(n, 1);x(n) = b(n) / A(n,n);for i = n-1:-1:1x(i) = (b(i) - A(i,i+1:n) * x(i+1:n)) / A(i,i);end
end% 使用例子
A = [2 -2 -1; 4 1 -2; -2 1 -1];
b = [-2; 1; -3];
x = Gauss(A, b);
disp(x);
2. 对1 中的线性方程组,利用LU 分解进行求解,并输出L 和U。
(注意将本部分代码封装为一个函数,函数名LU,该函数对应的文件同样命名为LU)。
function [L, U] = LU(A)[n,~] = size(A);L = eye(n);U = A;for k = 1:n-1for i = k+1:nfactor = U(i,k) / U(k,k);L(i,k) = factor;U(i,k:n) = U(i,k:n) - factor * U(k,k:n);endend
end% 使用例子
A = [2 -2 -1; 4 1 -2; -2 1 -1];
[L, U] = LU(A);
disp(L);
disp(U);
3. 对1 中的线性方程组,利用PA=LU 分解进行求解,并输出P、L 和U。
(注意将本部分代码封装为一个函数,函数名PLU,该函数对应的文件同样命名为PLU)。
function [P, L, U] = PLU(A)[n,~] = size(A);P = eye(n);L = zeros(n);U = A;for k = 1:n-1[~, maxindex] = max(abs(U(k:n,k)));maxindex = maxindex + k - 1;U([k,maxindex],:) = U([maxindex,k],:);L([k,maxindex],1:k-1) = L([maxindex,k],1:k-1);P([k,maxindex],:) = P([maxindex,k],:);for i = k+1:nfactor = U(i,k) / U(k,k);L(i,k) = factor;U(i,k:n) = U(i,k:n) - factor * U(k,k:n);endendL = L + eye(n);
end% 使用例子
A = [2 -2 -1; 4 1 -2; -2 1 -1];
[P, L, U] = PLU(A);
disp(P);
disp(L);
disp(U);
四、算法原理
1. 给出高斯消去法、LU 分解、PA=LU 分解的算法原理
-
高斯消去法
高斯消去法是一种用于解线性方程组的算法,它的目标是将给定的系数矩阵转化为上三角矩阵(或更进一步转化为对角矩阵),这样可以直接使用回代法求解未知数。步骤:
- 选取主元(通常是当前列下的最大绝对值元素)。
- 使用主元所在的行减去其他行,从而消去该列下主元以下的所有元素。
- 对下一个列重复以上步骤,直到整个矩阵成为上三角形态。
- 使用回代法求解未知数。
-
LU 分解
LU分解是将系数矩阵A分解为一个下三角矩阵L和一个上三角矩阵U的过程。这样原方程组Ax=b变为LUx=b,先解Ly=b得到y,再解Ux=y得到x。步骤:
- 从第一行开始,将A的当前行元素存储在U的相应位置,将除对角线元素外的当前列元素存储在L的相应位置。
- 使用L的当前列元素与U的当前行元素更新A的剩余部分。
- 对于下一个列重复上述步骤。
-
PA=LU 分解
有时直接的LU分解不可能或者数值上不稳定,这时可以通过行交换获得稳定性。PA=LU分解将A分解为一个置换矩阵P、一个下三角矩阵L和一个上三角矩阵U。步骤:
- 选择一个主元并进行必要的行交换。
- 按照LU分解的方法更新L和U的元素。
- 对下一个列重复以上步骤。
2. 分别给出高斯消去法、LU 分解消去和回代过程的耗费的计算量。
-
高斯消去法
消去过程的计算量大约为(2/3)n3,而回代过程为n2。所以总的计算量大约是O(n^3)。 -
LU 分解
LU分解的计算量和高斯消去法类似,主要来自于消去过程,大约为(2/3)n3。回代过程是O(n2),所以总的计算量仍然是O(n^3)。 -
PA=LU 分解
PA=LU分解的计算量和LU分解相似,因为增加的主要是行交换操作,这不会显著增加计算量。所以总的计算量仍然是O(n^3)。
五、测试数据及结果
-
给出算法输出的方程组的解。

-
给出算法输出的方程组的解及L 和U。
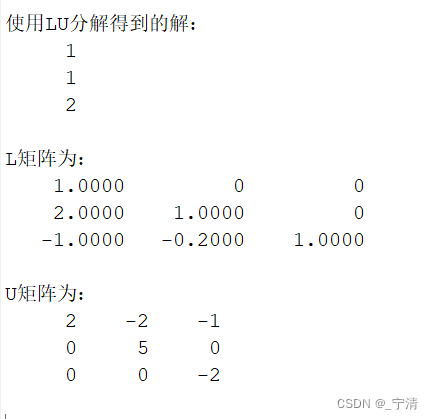
-
给出算法输出的方程组的解及P、L 和U。
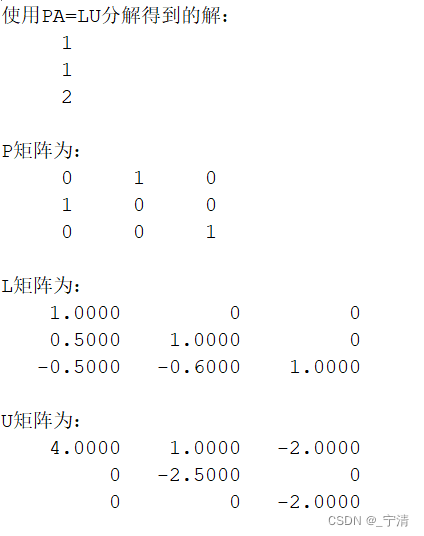
六、总结与思考
-
知识点的理解:
通过本次MATLAB实验,我深化了对线性代数中几个关键算法的理解:高斯消去法、LU分解和PA=LU分解。这些算法是解线性方程组的基石,并且在各种应用领域中都有广泛的使用。
-
代码实现的技巧:
- 使用MATLAB进行矩阵操作相对简单。例如,我们可以轻松地进行矩阵乘法、提取子矩阵和矩阵分解。
- 通过封装代码为函数,可以使整体代码结构更清晰、模块化,并增强代码的可读性和重用性。
- 适当的注释和文档对于理解和后期修改代码非常重要。
思考:
-
算法的应用:
虽然这三种算法在解决线性方程组方面很有用,但它们在处理大型矩阵或具有特定结构的矩阵时可能并不是最优的。例如,对于稀疏矩阵或对称正定矩阵,可能存在更高效的算法。考虑不同的问题背景和矩阵特点来选择合适的算法是很重要的。
-
数值稳定性:
实验中,我们简单地实现了上述算法,但在实际应用中,数值稳定性是一个需要考虑的重要问题。特别是在高斯消去法中,如果不适当地选择主元,可能会导致数值不稳定。这就是为什么PA=LU分解(带有行交换)在某些情况下更受欢迎。
-
优化与进一步学习:
MATLAB提供了一系列的内置函数和工具箱,例如
lu函数,可以直接进行LU分解。通过比较我们自己的实现和MATLAB的内置函数,我们可以进一步了解性能和数值稳定性的问题,并从中学习。
综上,本次MATLAB实验不仅加深了我计算方法的理解,而且让我认识到在实际应用中考虑算法的数值稳定性和选择最适合的算法的重要性。
相关文章:

高斯消去法 | LU分解 | PA=LU分解(MatLab)
一、问题描述 利用高斯消去法,LU 分解及PALU 分解求解非线性方程组。 二、实验目的 掌握高斯消去法、LU 分解、PALU 分解的算法原理;编写代码实现利用高斯消去法、LU 分解、PALU 分解来求解线性方程组。 三、实验内容及要求 1. 利用顺序高斯消去法求…...

Linux笔记之expect和bash脚本监听输出并在匹配到指定字符串时发送中断信号
Linux笔记之expect和bash脚本监听输出并在匹配到指定字符串时发送中断信号 code review! 文章目录 Linux笔记之expect和bash脚本监听输出并在匹配到指定字符串时发送中断信号1.expect2.bash 1.expect 在Expect脚本中,你可以使用expect来监听程序输出,…...

项目02《游戏-12-开发》Unity3D
基于 项目02《游戏-11-开发》Unity3D , 任务:实现场景怪物自动巡航 , 首先在场景中创建小球命名为路径点WayPoint0, 取消小球的碰撞器Collider, 再复制两个改名为WayPoint1 和 WayPoint2 , 在…...

记一次面试题
1.Php 私有化包(composer)的部署 1. 创建你的PHP包 确定你的包的功能和命名空间。 创建一个新的目录并初始化一个Git仓库。 使用composer init命令创建一个composer.json文件,并定义你的包名、版本、依赖等信息。 2. 开发并测试你的包 在本地…...

Rust入门2——随机数
文章目录 一、生成随机数二、比较两个数相等 简单列出两个Rust的小例子 一、生成随机数 在Cargo.toml的dependencies中引入rand,指定rand的版本 [dependencies] rand "^0.3.14"之后在主函数中调用rand函数,生成随机数 use rand::Rng; f…...

c#: 表达式树的简化
环境: .net 6 一、问题? 有下面的表达式: var nums new List<int> { 1, 2, 3 }; Expression<Func<int, bool>> exp i > i > nums.Max();我们知道,它其实就是:exp i > i > 3; 那么…...
13. UE5 RPG限制Attribute的值的范围以及生成结构体
前面几章,我们实现了通过GameplayEffect对Attribute值的修改,比如血量和蓝量,我们都是有一个最大血量和最大蓝量去限制它的最大值,而且血量和蓝量最小值不会小于零。之前我们是没有实现相关限制的,接下来,我…...

UE4运用C++和框架开发坦克大战教程笔记(十九)(第58~60集)完结
UE4运用C和框架开发坦克大战教程笔记(十九)(第58~60集)完结 58. 弹窗显示与隐藏59. UI 面板销毁60. 框架完成与总结 58. 弹窗显示与隐藏 这节课我们先来补全 TransferMask() 里对于 Overlay 布局类型面板的遮罩转移逻辑ÿ…...

ModuleNotFoundError: No module named ‘_ctypes‘报错解决方案
1、须命令安装libbffi-devel软件包: yum install libffi-devel -y2、安装完后再重装python3,无须卸载 找到之前的python3安装包,如果安装包删除了通过 history | grep python命令找到最初安装时的包下载的命令下载,保证版本一样&…...

【服务器数据恢复】服务器RAID模块硬件损坏的数据恢复案例
服务器数据恢复环境&故障: 某品牌服务器中有一组由数块SAS硬盘组建的RAID5磁盘阵列,服务器操作系统是WINDOWS SERVER,服务器中存放企业数据,无数据库文件。 服务器出故障之前出现过几次意外断电的情况,服务器断电…...

spring boot3x登录开发-上(整合jwt)
⛰️个人主页: 蒾酒 🔥系列专栏:《spring boot实战》 🌊山高路远,行路漫漫,终有归途。 目录 前置条件 jwt简介 导依赖 编写jwt工具类 1.配置项直接嵌入代码,通过类名.静态方法使用 2.配置项写到…...

git 克隆拉取代码出现私钥权限问题。
问题反馈: rootdd:~/android/boost-1.74-for-android-r20b# git clone https://github.com/liulilittle/boost-1.74-for-android-r20b.git Cloning into boost-1.74-for-android-r20b... WARNING: UNPROTECTED PRIVATE KEY FILE! Permissions 0777 for /root/…...
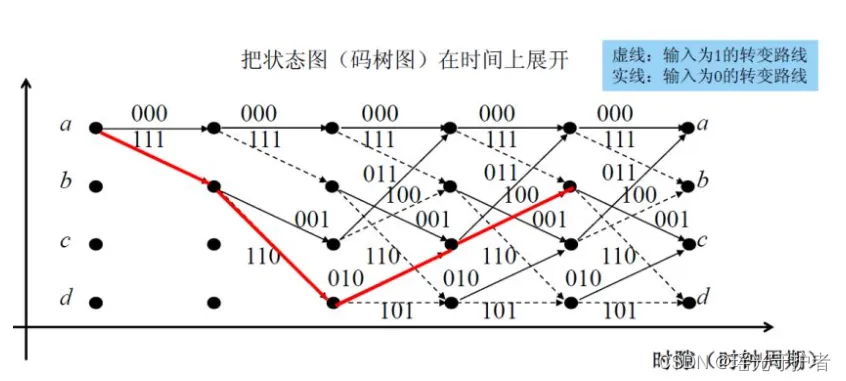
【5G NR】【一文读懂系列】移动通讯中使用的信道编解码技术-卷积码原理
目录 一、引言 二、卷积编码的发展历史 2.1 卷积码的起源 2.2 主要发展阶段 2.3 重要里程碑 三、卷积编码的基本概念 3.1 基本定义 3.2 编码器框图 3.3 编码多项式 3.4 网格图(Trellis)描述 四、MATLAB示例 一、引言 卷积编码,作为数字通信领域中的一项…...

揭开Markdown的秘籍:标题|文字样式|列表
🌈个人主页:聆风吟 🔥系列专栏:Markdown指南、网络奇遇记 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋前言一. ⛳️Markdown 标题二. ⛳️Markdown 文字样式2.1 🔔斜体2.2 &…...

移动最小二乘法
移动最小二乘法(Moving Least Square,MLS)主要应用于曲线与曲面拟合,该方法基于紧支撑加权函数(即函数值只在有限大小的封闭域中定义大于零,而在域外则定义为零)和多项式基函数,通过…...

【LeetCode】37. 解数独(困难)——代码随想录算法训练营Day30
题目链接:37. 解数独 题目描述 编写一个程序,通过填充空格来解决数独问题。 数独的解法需 遵循如下规则: 数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。&…...

VUE学习——属性绑定
属性绑定,就是给html添加id、class这样类似的操作。 <template><div v-bind:id"dynamicId"><div v-bind:class"dynamicClass">Test</div></div> </template><script>export default{data(){return{…...
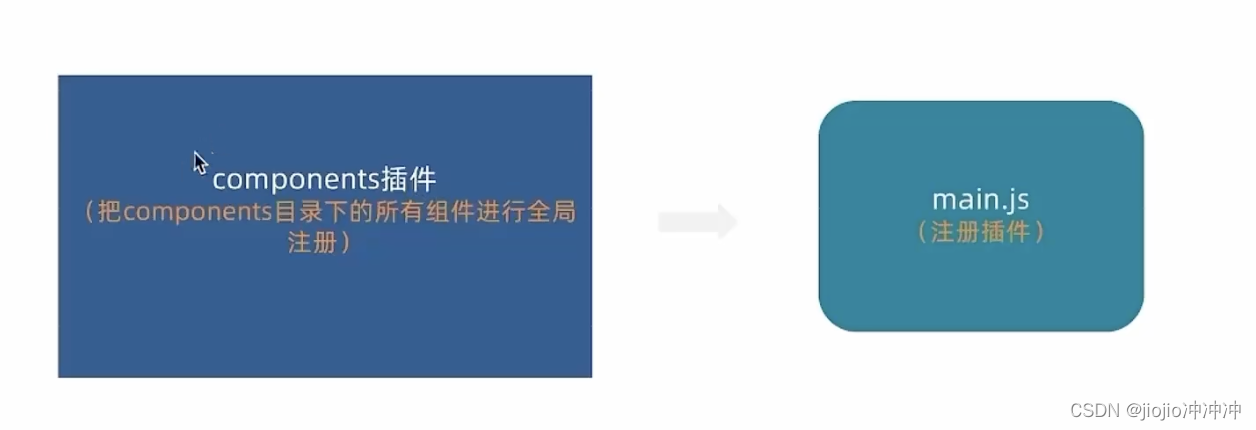
vue3 之 通用组件统一注册全局
components/index.js // 把components中的所组件都进行全局化注册 // 通过插件的方式 import ImageView from ./ImageView/index.vue import Sku from ./XtxSku/index.vue export const componentPlugin {install (app) {// app.component(组件名字,组件配置对象)…...
[Java][算法 双指针]Day 02---LeetCode 热题 100---04~07
LeetCode 热题 100---04~07 第一题:移动零 思路 找到每一个为0的元素 然后移到数组的最后 但是需要注意的是 要在给定的数组原地进行修改 并且其他非零元素的相对顺序不能改变 我们采用双指针法 定义两个指针i和j i和j一开始分别都在0索引位置 然后判断j所…...

【问题解决】如何将一个服务器的docker迁移到另一个服务器
要将Docker容器从一台机器迁移到另一台机器,可以按照以下步骤操作: 在机器A上提交容器为镜像: 使用docker commit命令将运行中的容器保存为新的镜像。这里需要容器的ID或名称,以及你想要命名的目标镜像名。 docker commit [容器…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...
