力扣精选算法100道—— 连续数组(前缀和专题)
连续数组(前缀和专题)
目录
🚩了解题意
🚩算法原理
❗为什么hash设置成<0,-1>键值对
❗与和为K的子数组比较hash的键值对
🚩代码实现
🚩了解题意

我们看到给定数组里面只有0和1,我们要找到一个连续的子数组具有相同数量的0和1,那么我们想想,如果我们给0代替成-1,那么-1 1 -1 1是不是等于0是不是相当于找到了具有相同数量的0和1了。
所以 我们首先要想到 将0改成-1 ,然后找到相同的0和1的数量就转换成在数组中最长的子数组中和为0.
这一题和 和为K的子数组 很像 ——和为0的子数组(我们只需要将0改成-1即可)
🚩算法原理
该函数的主要目的是找到nums中的一个最长的连续子数组,该子数组中0和1的数量相等。它使用了一个哈希表hash来记录当前累积和首次出现的位置,以便在后续遍历中可以计算当前累积和与首次出现位置之间的距离,从而得到最长的满足条件的子数组长度。
还是利用哈希+前缀和思路。但是这一题我们需要考虑到几个细节。
我们先给过程分析一下吧

- 创建一个无序哈希表
hash,用于存储累积和及其首次出现的位置。初始化时将累积和为0的位置设为-1,这样方便后续计算。 - 初始化两个整数变量
sum和ret,分别用于存储当前累积和和最长满足条件的子数组长度。 - 使用循环遍历
nums中的每个元素,对累积和进行更新。如果当前元素为0,则累积和加上-1,否则加上1。 - 在每次更新累积和后,检查哈希表中是否已经记录了当前累积和。如果已经记录,则计算当前位置与首次出现位置的距离,并更新最长子数组长度
ret。否则,将当前累积和及其位置记录到哈希表中。 - 最后,返回最长子数组长度
ret作为结果。
这段代码的时间复杂度为O(n),其中n是输入向量nums的长度。
这里有几个细节问题

为什么累积和为0的位置设为-1,我们根据一个情况来阐述吧
<0,-1>键值对,0代表前缀和,-1代表下标。
❗为什么hash设置成<0,-1>键值对
在这段代码中,将累积和为0的位置设为-1的目的是为了在计算最长子数组长度时能够正确处理从数组开头开始的子数组。

在遍历数组时,累积和为0意味着从数组开始到当前位置的子数组中0和1的数量相等。因此,如果在后续的遍历中再次遇到累积和为0,那么说明中间这段子数组中0和1的数量仍然相等。
如果没有将累积和为0的位置设为-1,而是设为0,那么在计算距离时可能会得到错误的结果。因为累积和为0的情况可能出现在数组的第一个位置,此时距离为当前位置减去0,会导致计算出的距离比实际子数组长度小1。
因此,将累积和为0的位置设为-1可以避免这种情况,确保计算出的最长子数组长度是正确的。
❗与和为K的子数组比较hash的键值对

hash[0] = 1 的目的是在处理前缀和时确保能够正确统计到和为k的子数组的数量。这是一个常用的技巧,主要是为了处理当前缀和恰好等于k的情况。
具体来说,hash 这个哈希表用于统计前缀和出现的次数。在初始化时,将累积和为0的次数设置为1是为了确保能够正确处理累积和等于k的情况。
考虑这样一种情况,如果数组中存在一个子数组的和正好等于k,那么这个子数组的前缀和减去k就等于0。因此,在遍历数组时,当遇到一个前缀和sum时,如果之前已经有一个前缀和sum - k存在,那么说明从那个前缀和到当前位置的子数组和正好为k。
举个例子,假设有数组 nums = [1, 2, 3],而 k = 3。在遍历过程中,前缀和依次为1、3、6,此时对于前缀和为3,前缀和为0的情况正好存在,这意味着从数组开头到当前位置的子数组和为3,满足条件。
因此,初始化时将 hash[0] = 1 是为了确保能够正确处理这种情况。
和为K的子数组:<0,1> 在和为K的子数组中0代表前缀和,1代表前缀和出现的次数
和为0的子数组:这一题<0,-1> 在和为0的子数组中 0代表前缀和,-1代表下标的位置。
🚩代码实现
class Solution {
public:int findMaxLength(vector<int>& nums) {unordered_map<int,int>hash;hash[0]=-1;int sum=0,ret=0;int dest=0;for(int i=0;i<nums.size();i++){sum+=nums[i]==0?-1:1;//如果sums[i]==0就改成-1,否则就是1if(hash.count(sum)) ret=max(ret,i-hash[sum]);else hash[sum]=i;//这里记录的是长度}return ret;}
};我们会一直一直在一起哒!
相关文章:

力扣精选算法100道—— 连续数组(前缀和专题)
连续数组(前缀和专题) 目录 🚩了解题意 🚩算法原理 ❗为什么hash设置成<0,-1>键值对 ❗与和为K的子数组比较hash的键值对 🚩代码实现 🚩了解题意 我们看到给定数组里面只有0和1,我们…...

flutter 国内源
Flutter 在中国由于网络原因,从官方默认的国外源下载Dart包和Flutter SDK可能会比较慢或者不稳定。为了加速依赖包的获取与Flutter SDK的安装,可以使用国内镜像源。以下是一些国内常用的Flutter和Dart包镜像源: 清华大学开源软件镜像站 Flu…...
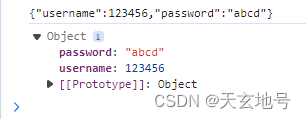
第九个知识点:内部对象
Date对象: <script>var date new Date();date.getFullYear();//年date.getMonth();//月date.getDate();//日date.getDay();//星期几date.getHours();//时date.getMinutes();//分date.getSeconds();//秒date.getTime();//获取时间戳,时间戳时全球统一&#x…...

Android 车载应用开发之车载操作系统
一、前言 到 2030 年,全球电动汽车的销量将超过 7000 万辆,保有量将达到 3.8 亿辆,全球年度新车渗透率有望触及 60% 。这一数据来自国际能源署(IEA)发布的《全球电动汽车展望2023》。 市场趋势和政策努力的双加持下,新能源汽车来势凶猛,燃油车保有量逐年递减。此番景象…...
)
Qt PCL学习(文章链接汇总)
Qt PCL学习(一):环境搭建 Qt PCL学习(二):点云读取与保存 Qt PCL学习(三):点云滤波 Qt PCL学习(四):点云关键点 持续更新中…...
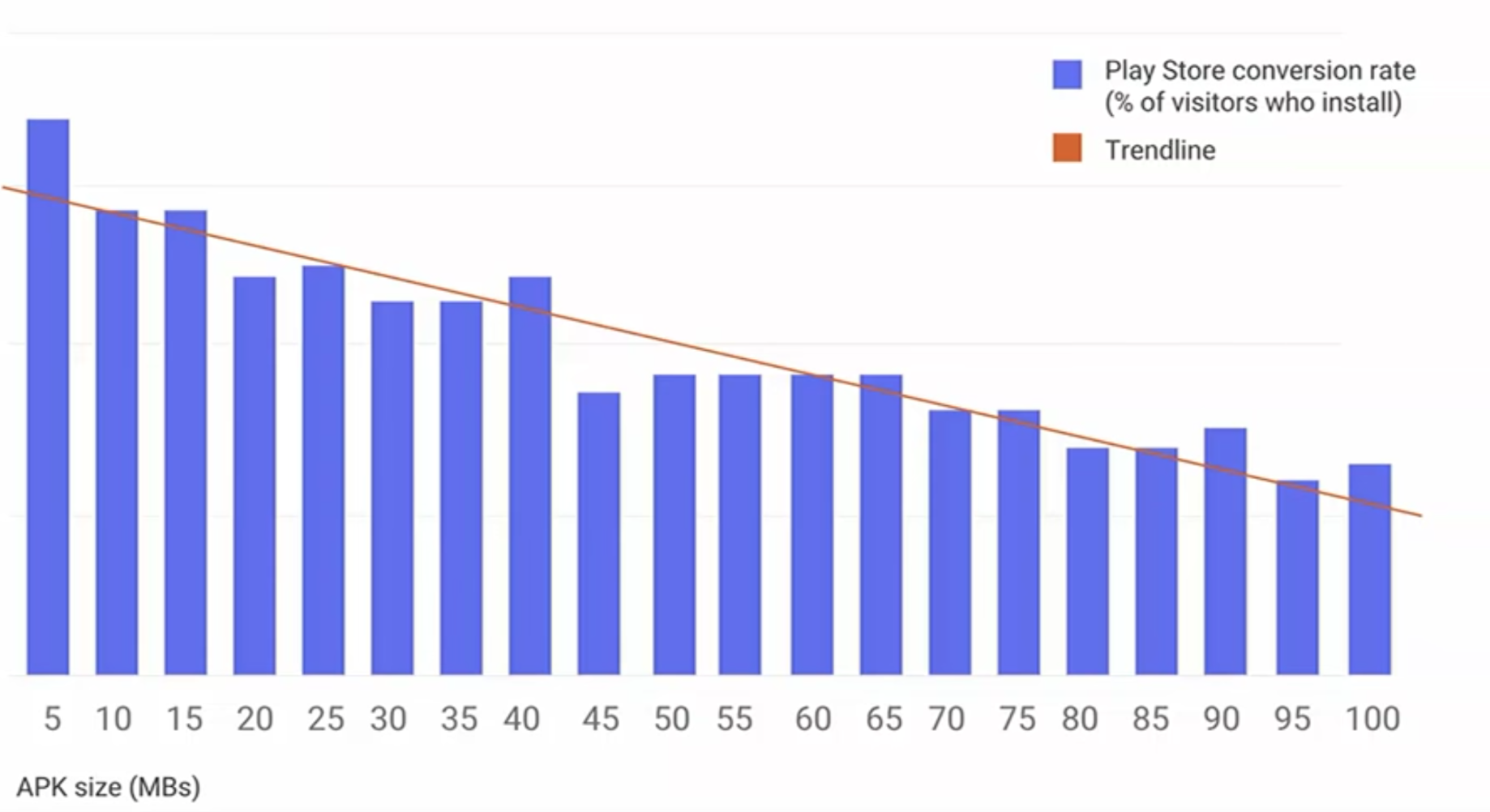
安卓动态链接库文件体积优化探索实践
背景介绍 应用安装包的体积影响着用户下载量、安装时长、用户磁盘占用量等多个方面,据Google Play统计,应用体积每增加6MB,安装的转化率将下降1%。 安装包的体积受诸多方面影响,针对dex、资源文件、so文件都有不同的优化策略&…...

[Java][算法 哈希]Day 01---LeetCode 热题 100---01~03
LeetCode 热题 100---01~03 ------->哈希 第一题 两数之和 思路 最直接的理解就是 找出两个数的和等于目标数 这两个数可以相同 但是不能是同一个数字(从数组上理解就是内存上不是同一位置) 解法一:暴力法 暴力解万物 按照需求 …...

【每日一题】LeetCode——链表的中间结点
📚博客主页:爱敲代码的小杨. ✨专栏:《Java SE语法》 | 《数据结构与算法》 | 《C生万物》 ❤️感谢大家点赞👍🏻收藏⭐评论✍🏻,您的三连就是我持续更新的动力❤️ 🙏小杨水平有…...

k8s 部署java应用 基于ingress+jar包
k8 集群ingress的访问模式 先部署一个namespace 命名空间 vim namespace.yaml kind: Namespace apiVersion: v1 metadata:name: ingress-testlabels:env: ingress-test 在部署deployment deployment是pod层一层封装。可以实现多节点部署 资源分配 回滚部署等方式。 部署的…...
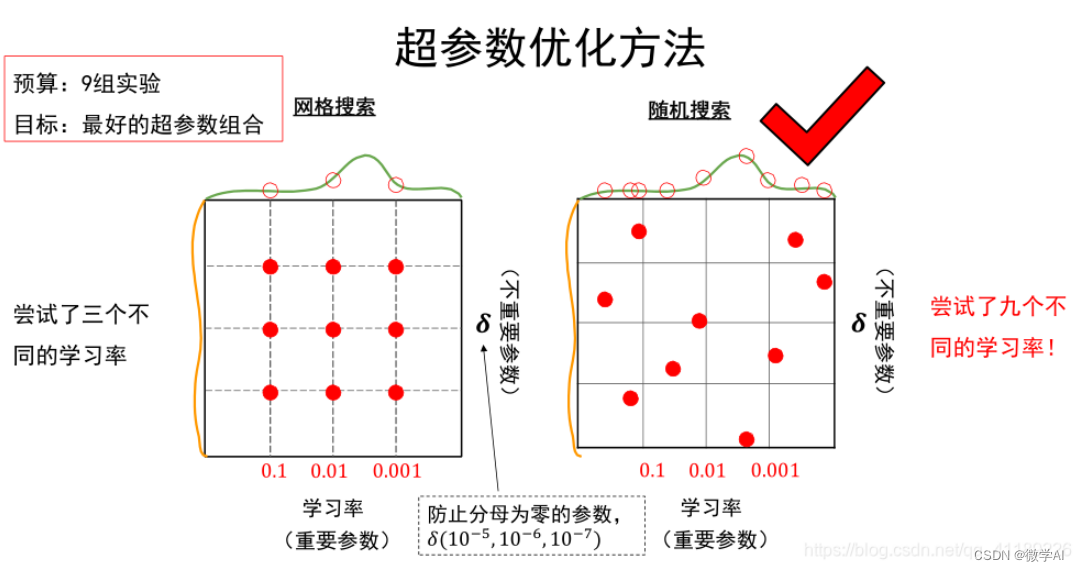
深度学习技巧应用36-深度学习模型训练中的超参数调优指南大全,总结相关问题与答案
大家好,我是微学AI,今天给大家介绍一下深度学习技巧应用36-深度学习模型训练中的超参数调优指南大全,总结相关问题与答案。深度学习模型训练中的调优指南大全概括了数据预处理、模型架构设计、超参数优化、正则化策略和训练技巧等多个关键方面,以提升模型性能和泛化能力。 …...

“探索AJAX:前端与后端数据交互的利器“
前言 在现代Web开发中,前端与后端之间的数据交互是一个至关重要的环节。为了实现无需刷新页面的动态更新,AJAX(Asynchronous JavaScript and XML)作为一种强大的技术被广泛应用。 AJAX的原理 AJAX通过JavaScript和XMLHttpReque…...

【5G NR】移动通讯中使用的信道编解码技术
目录 一、引言 二、信道编解码技术概述 三、移动通讯中常用的信道编解码技术 四、优缺点分析与比较 五、未来发展趋势 六、结论 本文主要介绍了移动通讯中采用的信道编解码技术,由于在5G NR终端中,通常要兼容4G LTE通讯技术,所以4G LTE…...

用Python Tkinter打造的精彩连连看小游戏【附源码】
文章目录 连连看小游戏:用Python Tkinter打造的精彩游戏体验游戏简介技术背景MainWindow类:职责:方法:Point类: 主执行部分:完整代码:总结: 连连看小游戏:用Python Tkinter打造的精彩游戏体验 在丰富多彩的游戏世界中,…...
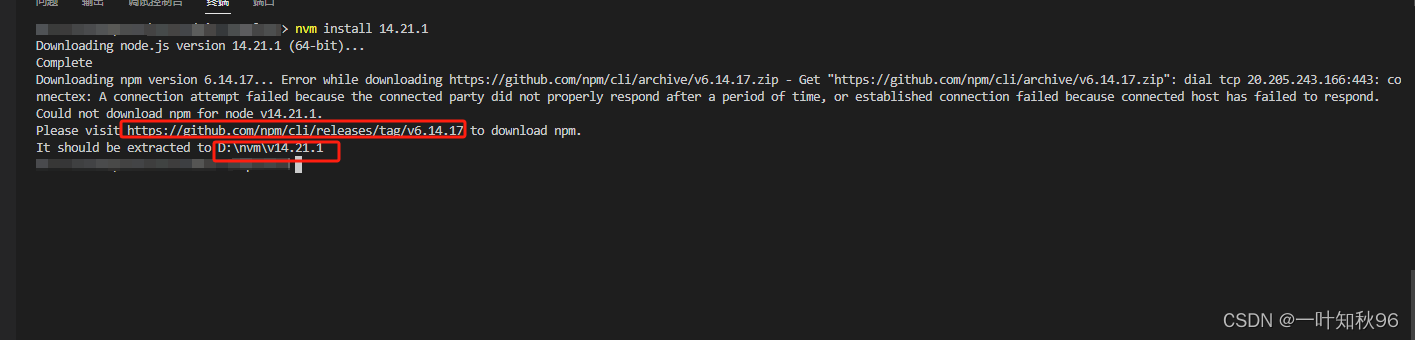
nvm安装node后,npm无效
类似报这种问题,是因为去github下载npm时下载失败, Please visit https://github.com/npm/cli/releases/tag/v6.14.17 to download npm. 第一种方法:需要复制这里面的地址爬梯子去下载(github有时不用梯子能直接下载,有…...
spring boot(2.4.x 开始)和spring cloud项目中配置文件application和bootstrap加载顺序
在前面的文章基础上 https://blog.csdn.net/zlpzlpzyd/article/details/136060312 spring boot 2.4.x 版本之前通过 ConfigFileApplicationListener 加载配置 https://github.com/spring-projects/spring-boot/blob/v2.3.12.RELEASE/spring-boot-project/spring-boot/src/mai…...

5-2、S曲线计算【51单片机+L298N步进电机系列教程】
↑↑↑点击上方【目录】,查看本系列全部文章 摘要:本节介绍S曲线的基本变换,将基本形式的S曲线变换成为任意过两点的S曲线,为后续步进电机S曲线运动提供理论支撑 一.计算目标 ①计算经过任意不同两点的S曲线方程 ②可调节曲线平…...

SQL 注入 - http头注入之UA头注入探测
环境准备:构建完善的安全渗透测试环境:推荐工具、资源和下载链接_渗透测试靶机下载-CSDN博客 一、http头注入介绍 HTTP头注入是一种网络安全攻击手段,它利用了Web应用程序对HTTP头的处理不当或缺乏充分的验证和过滤。在这种攻击中,攻击者通过修改HTTP请求头中的某些字段,…...

学习数据结构和算法的第5天
空间复杂度及其常见案例 空间复杂度 空间复杂度也是一个数学函数表达式,是对一个算法在运行过程中临时占用存储空间大小的量度。 空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度…...
 root方式)
Android 11 访问 Android/data/或者getExternalCacheDir() root方式
前言: 需求要求安装三方应用ExternalCacheDir()下载下来的apk文件。 getExternalCacheDir() : /storage/emulated/0/Android/data/com../cache/ 获取访问权限 如果手机安卓版本为Android10的时候,可以在AndroidManifest.xml中添加下列代码 android:requestLegacyExt…...
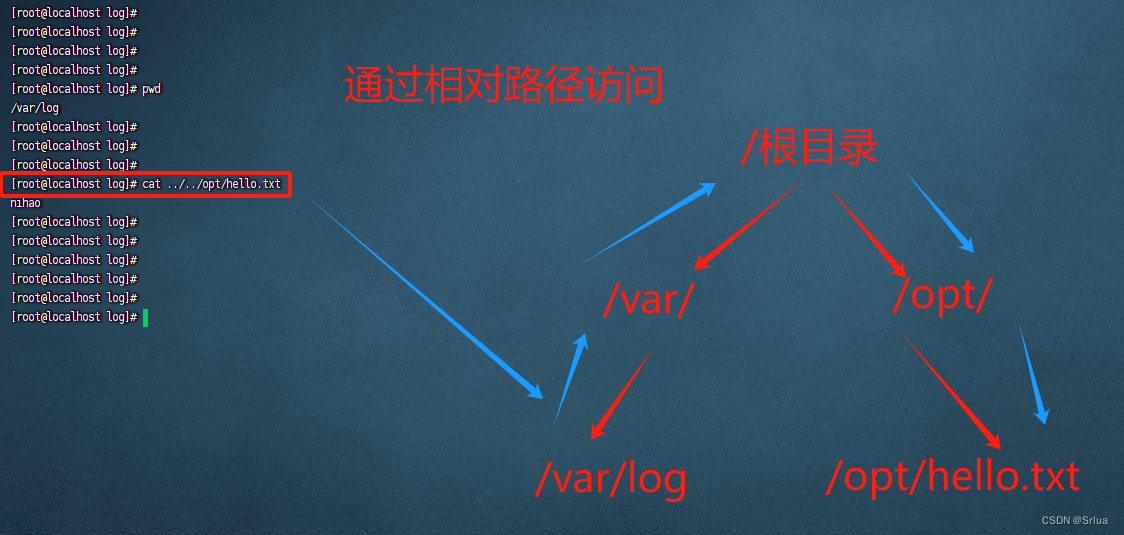
Linux探秘之旅:透彻理解路径、命令与系统概念
目录 如何远程连接 远程登录简明指南 linux区别 1.严格区分大小写 2.linux的命令返回结果判断 3.如何查看网络信息 4.关于后缀名(Linux不关心文件后缀) 4.1 需要记忆的后缀 5.echo命令 6.linux一切皆文件 6.1比如磁盘的文件 6.2可执行文件 …...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...
