【玩转408数据结构】线性表——定义和基本操作
考点剖析
线性表是算法题命题的重点,该类题目实现相对容易且代码量不高,但需要最优的性能(也就是其时间复杂度以及空间复杂度最优),这样才可以获得满分。所以在考研复习中,我们需要掌握线性表的基本操作,在平时多进行代码练习。当然在考场上,我们并不一定要求代码具有实际的可执行性,但我们需要去清晰的表达出算法的思路步骤,且算法题目只允许使用 C/C++ 语言进行实现。
线性表知识点
关于线性表这章内容其实并不多,我们将其分为两大部分:顺序存储(也就是我们常说的顺序表)和链式存储(链表),其中对于链表部分我们需要掌握其中的 单链表、双链表、循环链表、静态链表等部分链表。
关于线性表的内容并不是太难,我将用3-4篇文章带着大家一起了解线性表以及其实现,当我们可以自己去实现其功能的时候,我们对于该部分内容的知识掌握也就十分的熟练了,那么废话不多说,我们下面开始正式的进入线性表的学习。
线性表的定义
线性表是具有相同数据类型的 n ( n 0) 个数据元素的有限序列,其中n为表长;当n=0时,线性表为空表。在这里我们以L命名线性表,可以将其表示为:
其中: 是线性表的第一个元素,我们也称其为表头元素;
是线性表的最后一个元素,我们称其为表尾元素。
除了第一个元素外,每个元素有且仅有一个直接前驱(前一个元素);除了最后一个元素外,每个元素有且仅有一个直接后续(后一个元素)。当然我们也可以将“直接前驱”称为“前驱”,将“直接后续”称为“后续”。

通过已上知识我们总结出线性表的特点如下所示:
- 线性表元素个数有限
- 线性表元素都是数据元素,每个元素都是单个元素
- 线性表的元素具有逻辑上的顺序性,表中的元素有其先后次序
- 线性表的数据类型都相同,所以其每个元素所占空间大小相同
- 线性表的元素具有抽象性,我们讨论元素间的逻辑关系,不考虑元素究竟表示什么内容
注:线性表是逻辑结构,表示元素一对一的相邻关系,而我们前面所了解的链表以及顺序表指的是存储结构。(也就是说线性表的顺序存储是顺序表,线性表的链式存储是链表;这两个只是在存储结构上存在差异,而其逻辑结构归根结底都是线性表)。
线性表的基本操作
对于线性表,有一些基本操作是需要我们去学习的,至于为什么要学习这些基本操作,当然408大纲要求是要学习的,但在这里我们还是可以了解一下原因的。我们去对一些数据结构的基本操作进行封装实现,这样我们在进行复杂的操作时,可以去调用相关基本操作进行实现,并且这样进行封装也有利于减少错误的产生。
线性表的基本操作如下所示:
InitList(&L); //线性表的初始化
DestroyList(&L); //销毁线性表ListInsert(&L,i,e); //线性表的插入
ListDelete(&L,i,&e); //线性表的删除LocateElem(L,e); //按值查找
GetElem(L,i); //按位查找Length(L); //求线性表长
PrintList(L); //按顺序输出线性表的所有值
Empty(L); //判断线性表是否为空
(如果不懂为什么要加“&”的同学可以去学习一下,简单来说加“&”的元素我们可以修改其值,它会将其值带回来,而不加的我们在函数中修改其值是在主函数中无效的)。
注:在这里线性表只是一种逻辑结构,我们对于其基本操作的实现是要基于存储结构的,不同的存储结构实现其功能的方法是不同的,所以对于这些基本操作的实现,我会在后面顺序表和链表的讲解中进行代码的实现,在这里我们仅对其基本操作有一个了解即可。
小测试
- 线性表是一个可以存不同数据类型的n ( n
0) 个数据元素的有限序列吗?
- 在线性表中每一个元素都有自己的前驱和后续元素吗?
- 不同的线性表的逻辑结构必然存在一些差异性。对吗?
答案
-
错,线性表需要存储相同的数据类型。
-
错,第一个元素不存在前驱,最后一个元素不存在后续。
-
错,线性表的逻辑结构是相同的。
相关文章:
【玩转408数据结构】线性表——定义和基本操作
考点剖析 线性表是算法题命题的重点,该类题目实现相对容易且代码量不高,但需要最优的性能(也就是其时间复杂度以及空间复杂度最优),这样才可以获得满分。所以在考研复习中,我们需要掌握线性表的基本操作&am…...
回归预测 | Matlab实现ABC-BP人工蜂群算法优化BP神经网络多变量回归预测
回归预测 | Matlab实现ABC-BP人工蜂群算法优化BP神经网络多变量回归预测 目录 回归预测 | Matlab实现ABC-BP人工蜂群算法优化BP神经网络多变量回归预测预测效果基本描述程序设计参考资料 预测效果 基本描述 1.Matlab实现ABC-BP人工蜂群算法优化BP神经网络多变量回归预测&#x…...

SQL笔记-2024/01/31
cross join 两个表的笛卡尔积 例如: select s.name student_name,s.age student_age,s.class_id class_id,c.name class_name from student s cross join class c; 子查询 select s.name name,s.score score,s.class_id class_id from student s where s.class_id …...
)
C#系列-简介(1)
一,C#简介 C#(读作“C Sharp”)是一种由微软公司开发的、运行于.NET Framework和.NET Core(现在统称为.NET)之上的高级编程语言。C#结合了C的强大功能和Java的易用性,旨在成为一种“优雅且安全”的语言&am…...
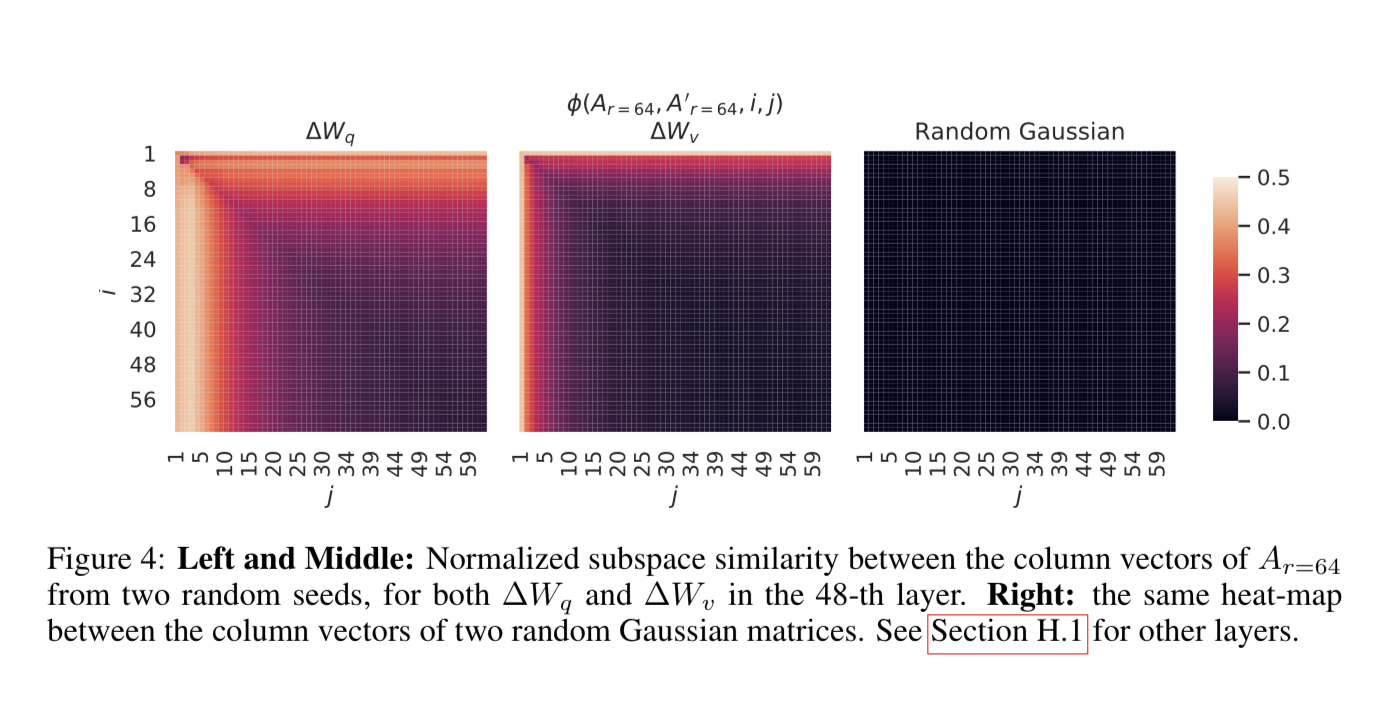
LoRA:语言模型微调的计算资源优化策略
编者按:随着数据量和计算能力的增加,大模型的参数量也在不断增加,同时进行大模型微调的成本也变得越来越高。全参数微调需要大量的计算资源和时间,且在进行切换下游任务时代价高昂。 本文作者介绍了一种新方法 LoRA,可…...
pycharm deployment 灰色 一直无法点击
我的development的配置如下,我看了很多教程一直不知道为什么一直是灰色的, 文件夹配置: 如果你这里 Autodect,那么你Mapping 的文件夹应该是应该省略这个前缀的,例如我下面,我应该将本地文件夹映射到/home…...
解决“使用Edge浏览器每次鼠标点击会出现一个黑色边框”的问题
目录 一 问题描述 二 解决方案 三 方案来源 四 参考资料 & AI工具 一 问题描述 为了方便进行收藏夹同步,开始从Chrome浏览器切换到Edge浏览器。在使用Edge浏览器过程中发现“每次鼠标点击会出现一个黑色边框”(效果如下图所示)&#…...

IEC61499 学习记录
IEC 61499是一种用于工业自动化的标准化模型,它基于面向对象的方法,用于描述分布式控制系统。该模型包括基本元素如事件、函数块和资源,以及它们之间的关系。函数块是该模型的核心概念,它们描述了系统中的控制和数据处理功能。整个…...
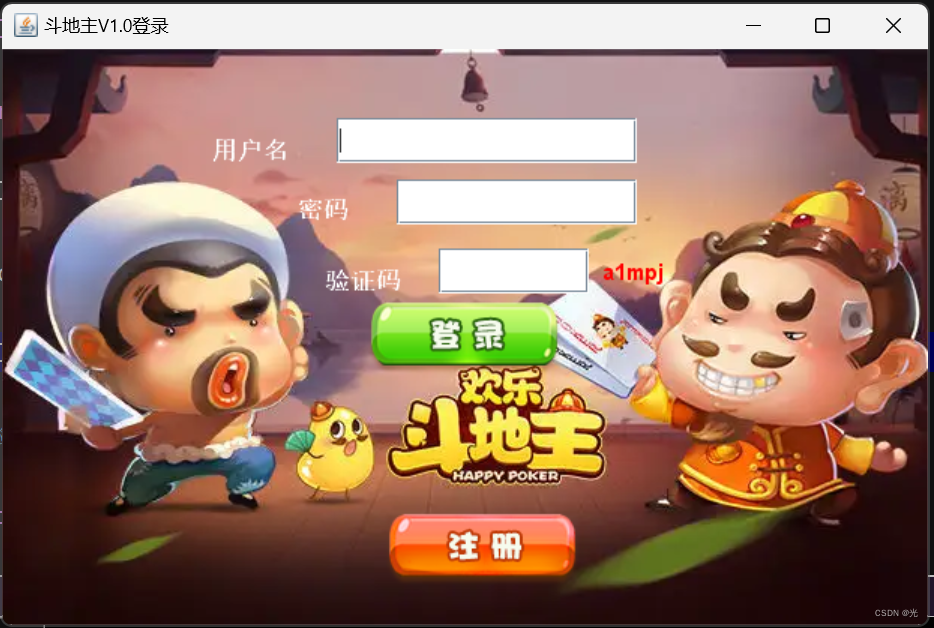
斗地主登录界面(JAVA图形化界面)设置
1.实现代码 import CodeUtil.CodeUtil; import domain.User;import javax.swing.*; import java.awt.*; import java.awt.event.MouseEvent; import java.awt.event.MouseListener; import java.util.ArrayList;public class LoginGame extends JFrame implements MouseListen…...
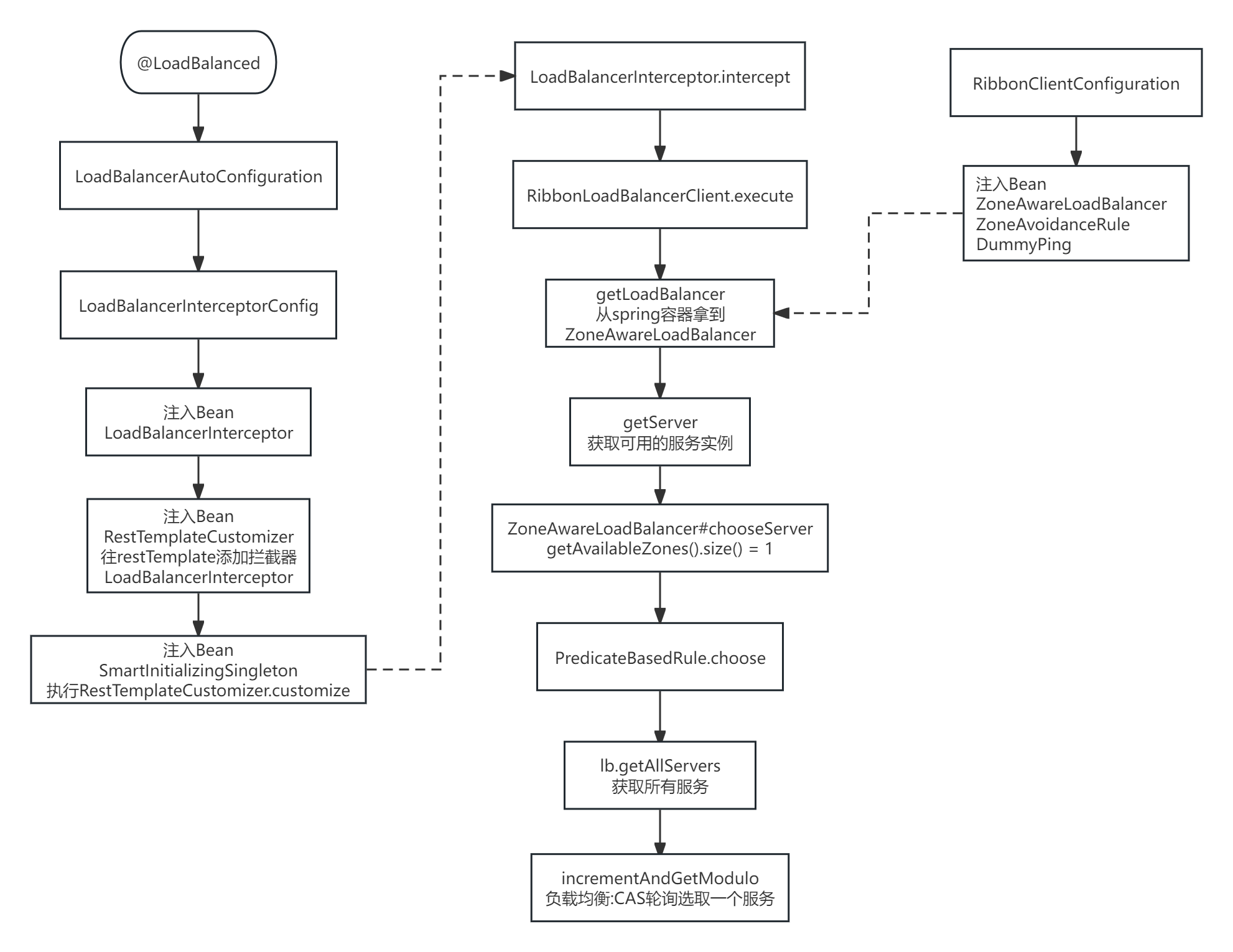
RibbonOpenFeign源码(待完善)
Ribbon流程图 OpenFeign流程图...

Python DNS操作详解
在网络世界中,DNS(Domain Name System)扮演着重要的角色,它是一种分布式数据库系统,用于将域名(如 google.com)转换为相应的 IP 地址(如 172.217.7.206)。DNS 可以被视为…...
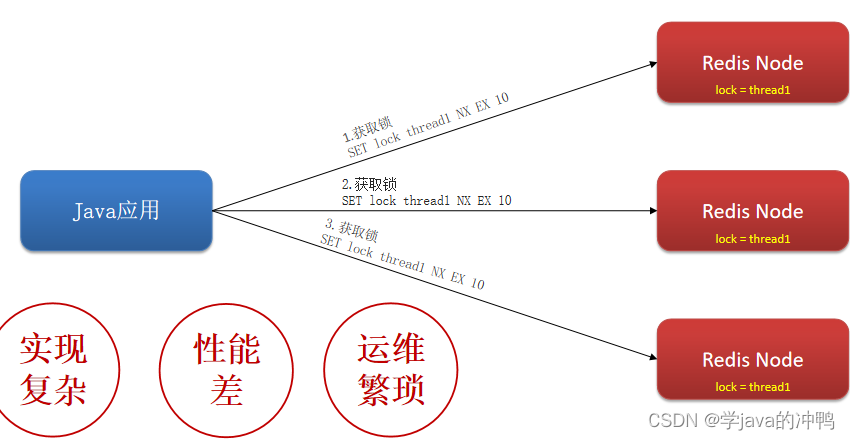
Redis篇之分布式锁
一、为什么要使用分布式锁 1.抢劵场景 (1)代码及流程图 (2)抢劵执行的正常流程 就是正好线程1执行完整个操作,线程2再执行。 (3)抢劵执行的非正常流程 因为线程是交替进行的,所以有…...

制作一个简单的HTML个人网页我的名字叫小明爱好打篮球,喜欢的歌手周杰伦我的技能java c++ python 主题配色蓝白
欢迎来到小明的个人网页 关于我 我叫小明,喜欢打篮球,最喜欢的歌手是周杰伦。 我的技能 JavaCPython 联系我 你可以通过以下方式联系我(请根据实际情况填写): 电子邮件:xiaomingexample.com GitHub&…...
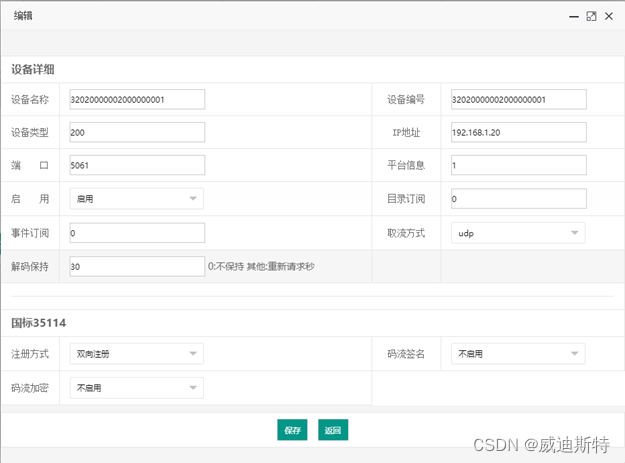
华为视频监控接入到视频监控平台 (华为网路监控摄像机IPC和华为视频节点设备VCN)
目 录 一、设备介绍 1.1 华为VCN介绍 1.2 AS-V1000视频监控平台介绍 1.3 平台服务器配置说明 二、安装、配置HW_IVS软件 2.1下载安装HW_IVS软件 2.2登录HW_IVS 2.3共享到外域 三、配置华为外域参数 3.1 PCG模块设置 3.2通信协议GBT28181配置 3.3传…...
树与二叉树---数据结构
树作为一种逻辑结构,同时也是一种分层结构,具有以下两个特点: 1)树的根结点没有前驱,除根结点外的所有结点有 且只有一个前驱。 2)树中所有结点可以有零个或多个后继。 树结点数据结构 满二叉树和完全二…...

C++ .h文件类的调用
demo1只有类的情况下调用 下面写一个util.h 文件里面 // 定义宏防止编译器重复编译 #ifndef TEST_H #define TEST_H class Test{ public:void sum(int a, int b);int num(int a, int b);bool number();}; #endif // TEST_H 调用的时候首先要引入这个头文件 #include "u…...
C语言:分支与循环
创造不易,友友们给个三连吧!! C语⾔是结构化的程序设计语⾔,这⾥的结构指的是顺序结构、选择结构、循环结构,C语⾔是能够实 现这三种结构的,其实我们如果仔细分析,我们⽇常所⻅的事情都可以拆分…...
【linux系统体验】-archlinux折腾日记
archlinux 一、系统安装二、系统配置及美化2.1 中文输入法2.2 安装virtualbox增强工具2.3 终端美化 三、问题总结3.1 终端中文乱码 一、系统安装 安装步骤人们已经总结了很多很全: Arch Linux图文安装教程 大体步骤: 磁盘分区安装 Linux内核配置系统(…...

常用数字处理格式校验
1、前端校验 1.1 要求为数字类型(不限位数与正负) input输入框添加 type“number” <el-input type"number"/>当typenumber时,仍然可以输入字母e或E。解决方法是:给typenumber的输入框添加一个正则表达式&…...

2024.1.26力扣每日一题——边权重均等查询
2024.1.26 题目来源我的题解方法一 使用dfs对每一组查询都求最近公共祖先(会超时,通不过)方法二 不需要构建图,直接在原始数组上进行求最大公共祖先的操作。 题目来源 力扣每日一题;题序:2846 我的题解 …...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...
