【最详解】如何进行点云的凹凸缺陷检测(opene3D)(完成度80%)
文章目录
- 前言
- 实现思路
- 想法1
- 想法2
- 想法3
- 补充
- 实现
- 想法1
- 想法2
- 代码
- 想法3
- 代码
- 总结
前言
读前须知:
首先我们得确保你已经完全知晓相关的基本的数学知识,其中包括用最小二乘法拟合曲二次曲面,以及曲面的曲率详细求解。若还是没弄清楚,则详细请看下面链接。
【点云、图像】学习中 常见的数学知识及其中的关系与python实战[更新中](建议从一个标题上从上往下看,比较循序渐进)
补充:曲率:反映曲面在某一点处的弯曲程度,它与该点及其邻近点的位置和法向量有关。
以及一些open3d的常见操作:
爆肝5万字❤️Open3D 点云数据处理基础(Python版)
先上结果:

实现思路
不同于常见的缺陷检测,如:划痕或者斑点这些肉眼可见的缺陷,凹凸性缺陷难以肉眼可见甚至得打光照射才能看见凹槽,这里我们使用深度摄像机(普通相机+深度信息),来采集深度信息。此时我们把图像称为深度图,当然深度图也可以转换为点云。
这里我们仅对点云这种数据进行处理。
要求:对异形曲面微细缺陷识别(我6月份之前要完成的毕设)
这里缺陷主要指凸起和凹槽。
想法1
想法1:如果是一个平面上出现凹槽或凸起的话,首先确立一个由大部分点拟合的平面,然后对不在此平面的点云进行高程分析,以确立凹陷或凸起程度。
(事实上不会很平,于是想法1排除,但可以用来做平面来做一个简单示例)
想法2
想法2:计算点云上每个点的领域曲率来描绘点的弯曲程度。
想法3
想法3:计算点云上每个点的高斯曲率和平均曲率来描绘点的弯曲程度。
补充
机器学习——详解KD-Tree原理
实现
想法1
暂无
想法2
想法2:
在求取完领域曲率的基础上,我们对其曲率的大小进行一个分割,并进行可视化。
这里进一步对这个领域曲率的定义进行详解。
首先,我们已经在这里的实战1了解到了领域曲率的求法。

基于邻域特征点提取和匹配的点云配准_李新春
可是这个定义我只在其他的博客中和下面这篇论文中找到定义,并无在wiki百科中找到相关阐述。
找了半天后依然无法解释其中原因,于是在参考了下面两篇博文后
如何理解矩阵特征值?
特征值的最大值与最小值
想出了这么一个合理的解释:
1、这个曲率定义的优点是,它不依赖于法向量的方向,而且它的值域是 [0, 1/3],这使得它比较容易进行归一化和可视化。
2、那么,为什么用最小的特征值除以特征值和,而不是用最大的特征值除以特征值和呢?
这是因为最小的特征值对应的特征向量是曲面的法向量,而最大的特征值对应的特征向量是曲面的主方向。
如果用最大的特征值除以特征值和,那么曲率的值就会与曲面的主方向的弯曲程度成正比,而与曲面的法向方向的弯曲程度无关。这样就会忽略掉曲面的凹凸变化,导致曲率的计算不准确。
如果用最小的特征值除以特征值和,那么曲率的值就会与曲面的法向方向的弯曲程度成正比,而与曲面的主方向的弯曲程度无关。这样就可以反映出曲面的凹凸变化,提高曲率的计算精度。
因此,用最小的特征值除以特征值和,而不是用最大的特征值除以特征值和,是为了更好地描述曲面的局部形状,而不是曲面的整体方向。
于是我们就可以坦然用这个定义来求取了。
代码
怕点云太多算不过来,首先对例子中的兔子点云进行了一个下采样。(如何获取兔子点云到时候再出教程)
import open3d as o3d
import numpy as npdef pca_compute(data, sort=True): #1、主成分分析average_data = np.mean(data, axis=0) # 求每一列的平均值,即求各个特征的平均值decentration_matrix = data - average_data # 去中心化矩阵H = np.dot(decentration_matrix.T, decentration_matrix) # 求协方差矩阵 #协方差是衡量两个变量关系的统计量,协方差为正表示两个变量正相关,为负表示两个变量负相关eigenvectors, eigenvalues, eigenvectors_T = np.linalg.svd(H) # 求特征值与特征向量 #H = UΣV^T #输出列向量、对角矩阵、行向量if sort:sort = eigenvalues.argsort()[::-1] # 从大到小排序 .argsort()是升序排序,[::-1]是将数组反转,实现降序排序eigenvalues = eigenvalues[sort] # 特征值 ## 使用索引来获取排序后的数组return eigenvaluesdef caculate_surface_curvature(radius,pcd):#2、计算点云的表面曲率cloud = pcdpoints = np.asarray(cloud.points) #点云转换为数组 点云数组形式为[[x1,y1,z1],[x2,y2,z2],...]kdtree = o3d.geometry.KDTreeFlann(cloud) #建立KDTreenum_points = len(cloud.points) #点云中点的个数curvature = [] # 储存表面曲率for i in range(num_points):k, idx, _ = kdtree.search_radius_vector_3d(cloud.points[i], radius) #返回邻域点的个数和索引neighbors = points[idx] #数组形式为[[x1,y1,z1],[x2,y2,z2],...]w = pca_compute(neighbors)#调用第1步 #由降序排序,w[2]为最小特征值 #np.zeros_like(w[2])生成与w[2]相同形状的全0数组delt = np.divide(w[2], np.sum(w)) #根据公式求取领域曲率curvature.append(delt)curvature = np.array(curvature, dtype=np.float64)return curvaturedef curvature_normal():#3、曲率归一化 从0-1/3归到0-1之间curvature = caculate_surface_curvature(radius,pcd) #调用第2步c_max = max(curvature)c_min = min(curvature)cur_normal = [(float(i) - c_min) / (c_max - c_min) for i in curvature] return cur_normaldef draw(cur_max,cur_min,pcd):#4、绘图cur_normal = curvature_normal()#调用第3步pcd.paint_uniform_color([0.5,0.5,0.5]) #初始化所有颜色为灰色for i in range(len(cur_normal)):if 0 < cur_normal[i] <= cur_min: #归一化后的曲率np.asarray(pcd.colors)[i] = [1, 0, 0]#红elif cur_min < cur_normal[i] <= cur_max:np.asarray(pcd.colors)[i] = [0, 1, 0]#绿elif cur_max < cur_normal[i] <= 1: np.asarray(pcd.colors)[i] = [0, 0, 1]#蓝# 可视化o3d.visualization.draw_geometries([pcd])cur_max = 0.7
cur_min = 0.3 #曲率分割基准
radius = 0.05
voxel_size = 0.01 #越小密度越大
pcd = o3d.io.read_point_cloud("bunny.pcd")
print(pcd)
pcd = pcd.voxel_down_sample(voxel_size) #下采样
draw(cur_max,cur_min,pcd)结果:

这个长度,宽度报错可以不管,有点子强迫症的可以在可视化改成:
o3d.visualization.draw_geometries([pcd],window_name="可视化原始点云",width=800, height=800, left=50, top=50,mesh_show_back_face=False)
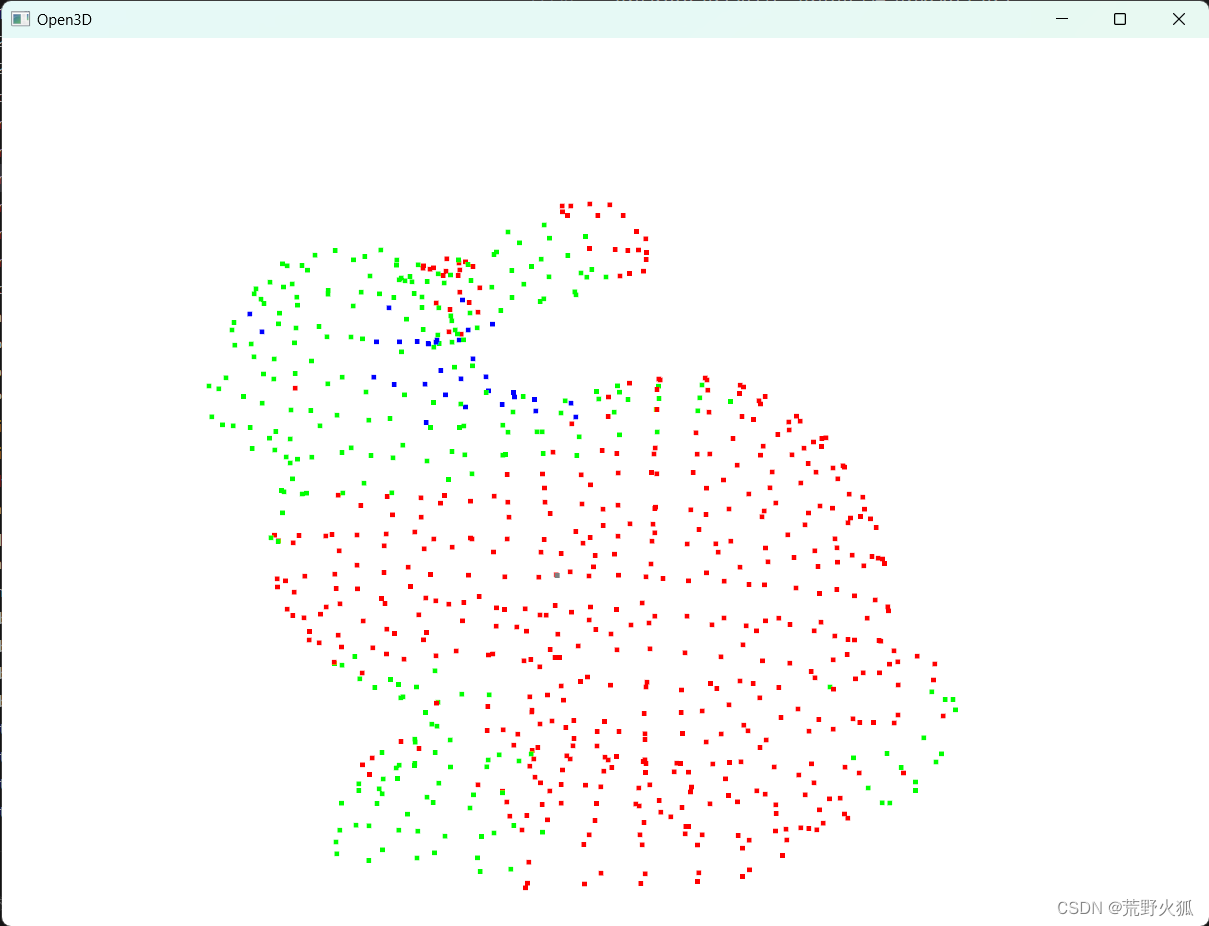
红色为曲率较低,绿色曲率中等,蓝色曲率较高。
发现效果上不太行,红色一些部分看着曲率也很高,甚至还出现了一个初始化时候的灰点,可能求邻近点的时候没取到?不曾得知。
想法3
首先我们在这里的高斯曲率和平均曲率求解有了一些认识。
附一张图:
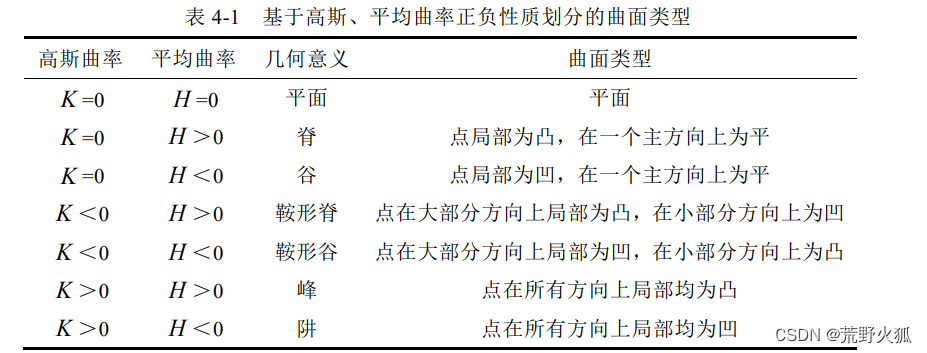
代码
import open3d as o3d
import numpy as np
from scipy.optimize import curve_fitvoxel_size = 0.01 #越小密度越大
radius = 0.07
pcd = o3d.io.read_point_cloud("bunny.pcd")
pcd = pcd.voxel_down_sample(voxel_size) #下采样
cloud = pcd
points = np.asarray(cloud.points) #点云转换为数组 点云数组形式为[[x1,y1,z1],[x2,y2,z2],...]
kdtree = o3d.geometry.KDTreeFlann(cloud) #建立KDTree
num_points = len(cloud.points) #点云中点的个数
pcd.paint_uniform_color([1, 0, 0]) # 初始化所有颜色为红色
# 定义非线性函数,这里假设是一个二次曲面
def func(x, a, b, c, d, e, f):return a * x[0]**2 + b * x[1]**2 + c * x[0] * x[1] + d * x[0] + e * x[1] + f
def f(x, y):return popt[0]*x**2 +popt[1]*y**2 +popt[2]* x*y +popt[3]*x + popt[4]*y +popt[5]
# 定义曲面的梯度函数,即一阶偏导数
def gradient(f, x, y):# 使用中心差分法近似求导 #参考https://cloud.tencent.com/developer/article/1685164h = 1e-6 # 差分步长,可以根据精度要求调整df_dx = (f(x + h, y) - f(x - h, y)) / (2 * h) # 对x求偏导df_dy = (f(x, y + h) - f(x, y - h)) / (2 * h) # 对y求偏导return df_dx, df_dy
# 定义曲面的曲率函数,即二阶偏导数
def curvature(f, x, y):# 使用中心差分法近似求导h = 1e-6 # 差分步长,可以根据精度要求调整d2f_dx2 = (f(x + h, y) - 2 * f(x, y) + f(x - h, y)) / (h ** 2) # 对x求二阶偏导d2f_dy2 = (f(x, y + h) - 2 * f(x, y) + f(x, y - h)) / (h ** 2) # 对y求二阶偏导d2f_dxdy = (f(x + h, y + h) - f(x + h, y - h) - f(x - h, y + h) + f(x - h, y - h)) / (4 * h ** 2) # 对xy求混合偏导# 根据公式计算高斯曲率K和平均曲率Hdf_dx, df_dy = gradient(f, x, y) # 调用梯度函数求一阶偏导E = 1 + df_dx ** 2F = df_dx * df_dyG = 1 + df_dy ** 2L = d2f_dx2 / np.sqrt(1 + df_dx ** 2 + df_dy ** 2) #np.sqrt()表示开方M = d2f_dxdy / np.sqrt(1 + df_dx ** 2 + df_dy ** 2)N = d2f_dy2 / np.sqrt(1 + df_dx ** 2 + df_dy ** 2)K = (L * N - M ** 2) / (E * G - F ** 2) # 高斯曲率H = (E * N + G * L - 2 * F * M) / (2 * (E * G - F ** 2)) # 平均曲率return K, Hcurvatures = []
for i in range(num_points):k, idx, _ = kdtree.search_radius_vector_3d(cloud.points[i], radius) #返回邻域点的个数和索引neighbors = points[idx] #数组形式为[[x1,y1,z1],[x2,y2,z2],...]#print(k)Y = neighbors[:, 2] # 因变量X = neighbors[:, [0,1]] # 自变量 [[2,3],[1,1],[8,9],[11,12],[4,5],[8,9]] 6*2popt, pcov = curve_fit(func, xdata=X.T,ydata= Y)x = cloud.points[i][0] # 某一点的x坐标y = cloud.points[i][1] # 某一点的y坐标K, H = curvature(f, x, y) # 计算该点的曲率curvatures.append([K,H])print(curvatures)
for i in range(len(curvatures)):if -0.05<curvatures[i][0] < 0.05 and -0.05<curvatures[i][1] <0.05: #平坦np.asarray(pcd.colors)[i] = [0, 0, 0]#黑elif -0.05<curvatures[i][0] < 0.05 and curvatures[i][1] >0.05: #凸np.asarray(pcd.colors)[i] = [1, 0, 0]#红elif -0.05<curvatures[i][0] < 0.05 and -0.05<curvatures[i][1] <0.05: #凹np.asarray(pcd.colors)[i] = [0, 1, 0]#绿elif curvatures[i][0] < -0.05 and curvatures[i][1] >0.05: #鞍形脊 大部分凸,少部分凹np.asarray(pcd.colors)[i] = [0, 0, 1]#蓝elif curvatures[i][0] < -0.05 and curvatures[i][1] <-0.05: #鞍形谷 大部分凹,少部分凸np.asarray(pcd.colors)[i] = [0, 1, 1]#青elif curvatures[i][0] > 0.05 and curvatures[i][1] >0.05: #峰 np.asarray(pcd.colors)[i] = [1, 0, 1]#紫elif curvatures[i][0] > 0.05 and curvatures[i][1] <-0.05: #阱np.asarray(pcd.colors)[i] = [1, 1, 0]#黄#显示点云
o3d.visualization.draw_geometries([pcd])结果:

结果出奇的好,每个点都进行了划分,比想法1好太多了。这里暂时用兔子点云测试,到时候创造一些平面点云再来测试一下。
总结
学习东西都不是一蹴而就的,果然还是得一步一步脚踏实地地学才学的明白。chatgpt是个好东西,只有你也会点东西时,它才会回答的正确,不能轻信之。
未完成:
ps:1、兔子点云pcd读取
2、创建平面点云
3、返回面积、深度信息
相关文章:

【最详解】如何进行点云的凹凸缺陷检测(opene3D)(完成度80%)
文章目录 前言实现思路想法1想法2想法3 补充实现想法1想法2代码 想法3代码 总结 前言 读前须知: 首先我们得确保你已经完全知晓相关的基本的数学知识,其中包括用最小二乘法拟合曲二次曲面,以及曲面的曲率详细求解。若还是没弄清楚࿰…...

海外云手机——平台引流的重要媒介
随着互联网的飞速发展,跨境电商、短视频引流以及游戏行业等领域正经历着迅猛的更新换代。在这个信息爆炸的时代,流量成为至关重要的资源,而其中引流环节更是关乎业务成功的关键。海外云手机崭露头角,成为这一传播过程中的重要媒介…...

数据库-计算机三级学习记录-4DBAS功能概要设计
DBAS功能概要设计 参照b站【计算机三级数据库技术】 DBAS功能设计包括应用软件中的数据库事务设计和应用程序设计。 功能设计过程一般被划分为总体设计、概要设计和详细设计。而具体到数据库事务设计部分,又可分成事务概要设计和事务详细设计。完成系统设计工作之后…...

JVM-虚拟机栈
虚拟机栈 Java虚拟机栈(Java Virtual Machine Stack)采用栈的数据结构来管理方法调用中的基本数据,先进后出(First In Last Out),每一个方法的调用使用一个栈帧(Stack Frame)来保存。 接下来以…...

linux系统上tomcat简介以及安装tomcat
tomcat简介以及安装 Tomcat简介安装环境安装jdk安装tomcat浏览器访问 Tomcat简介 Tomcat是一个开源的Web服务器和servlet容器,由Apache软件基金会开发和维护。它是一种流行的Java Web应用服务器,用于运行Java编写的Web应用程序。 Tomcat提供了一个轻量级…...
树莓派的pip安装时候添加清华源
每次都要去找镜像网址,太麻烦了,通过改配置可以一次性解决。 首先创建一个.pip 目录 mkdir ~/.pip意味着在当前目录下创建.pip文件,不过这个是隐藏文件,一般情况下是关闭隐藏文件的可视的,于是我绕了点弯弯。 编辑…...
共享网盘系统PHP源码
新V5.0版本,支持上传视频、支持视频播放、支持共享,也可以自己用。 可以自动生成视频外链,下载地址,播放器代码,html代码,ubb代码等等。 使用方法: 源码上传到服务器,打开网站根据…...
unity-ios-解决内购商品在Appstore上面已配置,但在手机测试时却无法显示的问题
自己这几天用 unity 2021 xcode 14.2 开发ios内购,appstore上面内购商品都已经配置好了,但是在手机里就是不显示,最后才发现必需得满足以下条件才行: 1. Appstore后台 -> 内购商品 -> 商品状态必需为『准备提交』以上状态…...
)
flask的基本使用 token插件(二)
一、安装flask-jwt-extended 安装flask-jwt-extend得时候 会自动安装一个pyjwt得库。pyjwt可以直接使用来生成JWT和验证。但是在flask中,可以通过Flask-JWT-Extended来实现JWT能,因为他封装了使用方式,以及一些属性和装饰器,用起…...
云计算、Docker、K8S问题
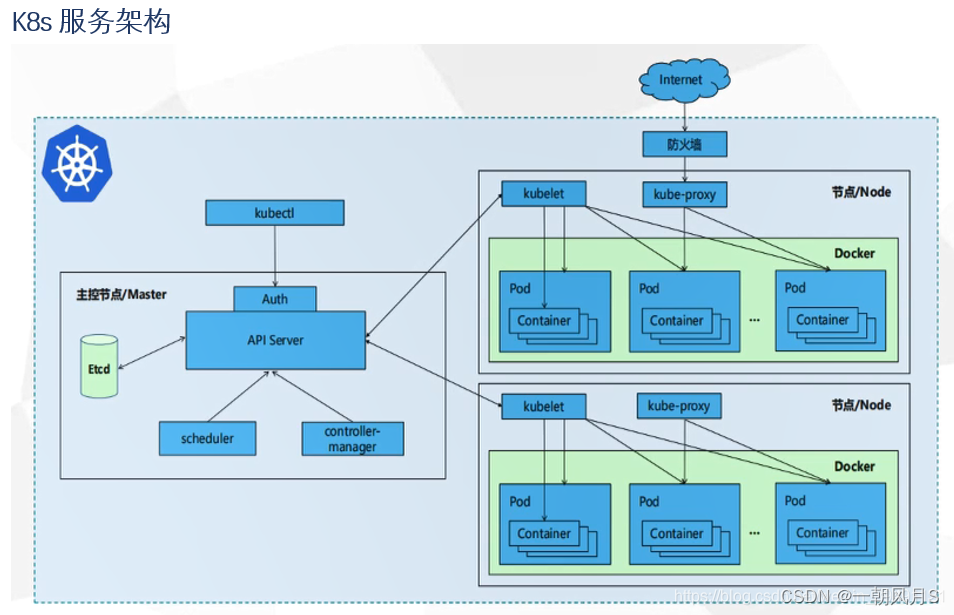
1 云计算 云计算作为一种新兴技术,已经在现代社会中得到了广泛应用。它以其高效、灵活和可扩展特性,成为了许多企业和组织在数据处理和存储方面的首选方案。 1.1 什么是云计算?它有哪些特点? 云计算是一种通过网络提供计算资源…...
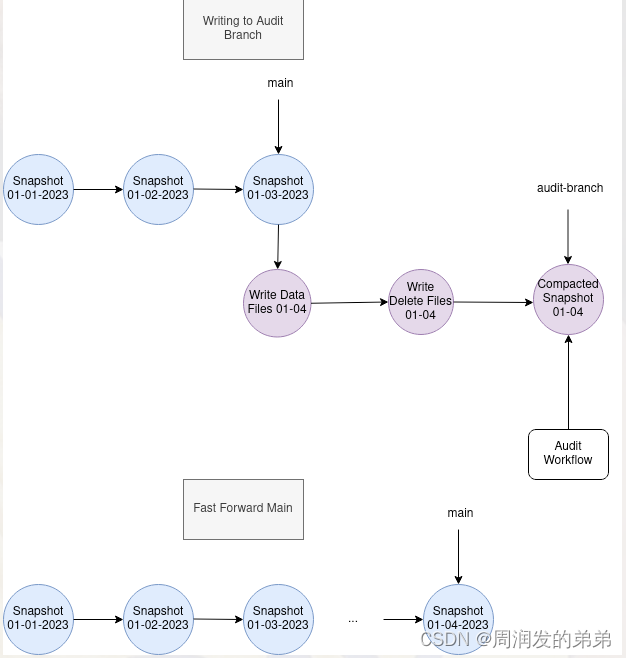
【Iceberg学习二】Branch和Tag在Iceberg中的应用
Iceberg 表元数据保持一个快照日志,记录了对表所做的更改。快照在 Iceberg 中至关重要,因为它们是读者隔离和时间旅行查询的基础。为了控制元数据大小和存储成本,Iceberg 提供了快照生命周期管理程序,如 expire_snapshots…...

在 Blazor WASM 中手撸一个.NET MD5类
最近.net8 blazor auto大火, 我也玩了一下,发现ssr能用的代码 MD5 类在wasm是没法用的. 于是搜索了一下互联网,找到了一份代码,分享给大家. 我找到的帖子作者原话: 代码不是我的,但我确实稍微修改了它以使其与 System.Security.Cryptography.MD5 类更加一致。 pub…...
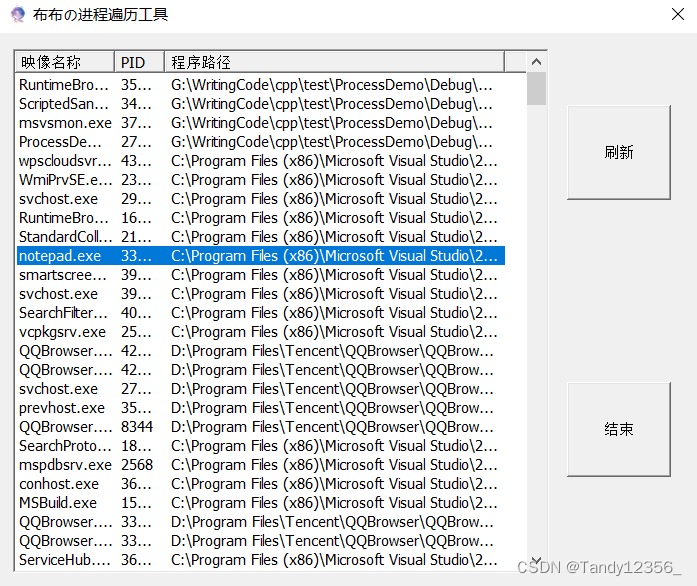
MFC实现遍历系统进程
今天我们来枚举系统中的进程和结束系统中进程。 认识几个API 1)CreateToolhelp32Snapshot 用于创建系统快照 HANDLE WINAPI CreateToolhelp32Snapshot( __in DWORD dwFlags, //指定快照中包含的系统内容__in DWORD th32P…...

【C语言】深入理解指针
目录 1.字符指针 2.指针数组 3.数组指针 4.数组传参与指针传参 一维数组传参 二维数组传参 一级指针传参 二级指针传参 5.函数指针 6.函数指针数组 7.指向函数指针数组的指针(了解即可) 8.回调函数 回调函数的应用:库函数qsort …...
Excel——有效性、二级菜单联动
一、录入规范数据 1.手动输入序列录入有效性信息 选择需要录入有效性的所有单元格 选择【数据】——【有效性】——【有效性】 在【允许】输入的值之间选择【序列】 在【序列】输入框中输入想要选择的值,中间用逗号(必须是英文逗号)隔开 。…...

计算机网络总结
1. 网络分层 网络上进行协议分层的好处 ①分层之后层次之间的耦合程度比较低,上层协议不必了解下层的细节,下层也不必了解上层的细节; ②方便的对某一层的协议进行替换; 真实网络的协议分层 OSI 七层网络模型(教科书&…...

初识文件包含漏洞
目录 什么是文件包含漏洞? 文件包含的环境要求 常见的文件包含函数 PHP伪协议 file://协议 php://协议 php://filter php://input zip://、bzip2://、zlib://协议 zip:// bzip2:// zlib:// data://协议 文件包含漏洞演示 案例1:php://inp…...

AR特效自研AI算法技术解决方案
在当今这个高速发展的数字化时代,增强现实(AR)技术已经成为企业创新和市场竞争的重要手段。美摄科技凭借对AI技术的深厚积累,为企业提供了一套创新的AR特效自研AI算法技术解决方案,旨在满足企业在AR领域的多元化需求。…...
)
牛客2024年除夕娱乐赛(题解)
比赛地址 : 牛客竞赛_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJ A 看题面然后猜!!! #include<bits/stdc.h> using namespace std; int main(){cout << "原神启动" << endl; } B 也是看题面然后猜 : #include<bits/stdc.…...

5 scala的函数式编程简介
与Java一样,Scala 也是使用 Lambda 表达式实现函数式变成的。 1 遍历 除了使用 for 可以对数组、List、Set 进行遍历外,也可以使用 foreach 函数式编程进行遍历,使代码更为简洁。 foreach 的方法签名为: foreach(f: (A) > …...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...
