C#,十进制展开数(Decimal Expansion Number)的算法与源代码
1 十进制展开数
十进制展开数(Decimal Expansion Number)的计算公式:
DEN = n^3 - n - 1
The decimal expansion of a number is its representation in base -10 (i.e., in the decimal system). In this system, each "decimal place" consists of a digit 0-9 arranged such that each digit is multiplied by a power of 10, decreasing from left to right, and with a decimal place indicating the s place.
2 计算结果
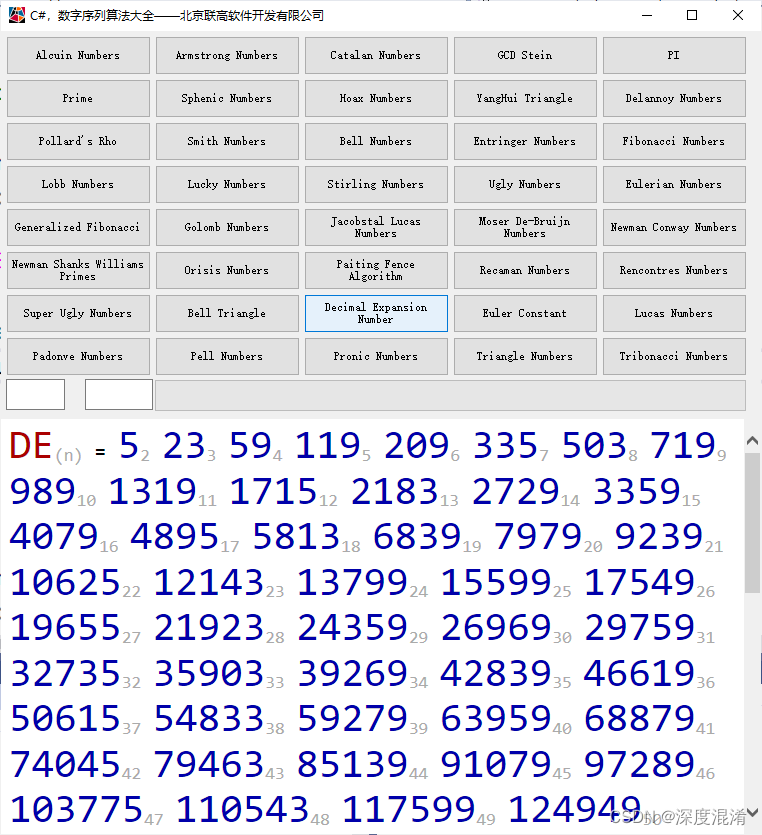
3 源程序
using System;
namespace Legalsoft.Truffer.Algorithm
{
public static partial class Number_Sequence
{
public static int Decimal_Expansion_Number(int n)
{
return n * n * n - n - 1;
}
}
}
The decimal expansion of a number is its representation in base-10 (i.e., in the decimal system). In this system, each "decimal place" consists of a digit 0-9 arranged such that each digit is multiplied by a power of 10, decreasing from left to right, and with a decimal place indicating the s place. For example, the number with decimal expansion 1234.56 is defined as
Expressions written in this form (where negative are allowed as exemplified above but usually not considered in elementary education contexts) are said to be in expanded notation.
Other examples include the decimal expansion of given by 625, of given by 3.14159..., and of given by 0.1111.... The decimal expansion of a number can be found in the Wolfram Language using the command RealDigits[n], or equivalently, RealDigits[n, 10].
The decimal expansion of a number may terminate (in which case the number is called a regular number or finite decimal, e.g., ), eventually become periodic (in which case the number is called a repeating decimal, e.g., ), or continue infinitely without repeating (in which case the number is called irrational).
The following table summarizes the decimal expansions of the first few unit fractions. As usual, the repeating portion of a decimal expansion is conventionally denoted with a vinculum.
4 代码格式
using System;namespace Legalsoft.Truffer.Algorithm
{public static partial class Number_Sequence{public static int Decimal_Expansion_Number(int n){return n * n * n - n - 1;}}
}
相关文章:

C#,十进制展开数(Decimal Expansion Number)的算法与源代码
1 十进制展开数 十进制展开数(Decimal Expansion Number)的计算公式: DEN n^3 - n - 1 The decimal expansion of a number is its representation in base -10 (i.e., in the decimal system). In this system, each "decimal place…...
Vue3快速上手(一)使用vite创建项目
一、准备 在此之前,你的电脑,需要安装node.js,我这边v18.19.0 wangdymb 2024code % node -v v18.19.0二、创建 执行npm create vuelatest命令即可使用vite创建vue3项目 有的同学可能卡主不动,可能是npm的registry设置的问题 先看下&#x…...
使用navicat导出mysql离线数据后,再导入doris的方案
一、背景 doris本身是支持直接从mysql中同步数据的,但有时候,客户不允许我们使用doris直连mysql,此时就需要客户配合将mysql中的数据手工导出成离线文件,我们再导入到doris中 二、环境 doris 1.2 三、方案 doris支持多种导入…...

re:从0开始的CSS学习之路 1. CSS语法规则
0. 写在前面 现在大模型卷的飞起,感觉做页面的活可能以后就不需要人来做了,不知道现在还有没有学前端的必要。。。 1. HTML和CSS结合的三种方式 在HTML中,我们强调HTML并不关心显示样式,样式是CSS的工作,现在就轮到C…...
npm install express -g报错或一直卡着,亲测可解决
问题描述: 最近学习vue3前端框架,安装Node.js之后,在测试是否可行时,cmd窗口执行了:npm install express -g,发现如下图所示一直卡着不动,最后还报错了,网上找了好久,各…...

机器学习11-前馈神经网络识别手写数字1.0
在这个示例中,使用的神经网络是一个简单的全连接前馈神经网络,也称为多层感知器(Multilayer Perceptron,MLP)。这个神经网络由几个关键组件构成: 1. 输入层 输入层接收输入数据,这里是一个 28x…...
vscode wsl远程连接 权限问题
问题描述:执行命令时遇到Operation not permitted 和 Permission denied问题,是有关ip地址和创建文件的权限问题,参考网络上更改wsl.conf文件等方法均无法解决,只能加sudo来解决...

VED-eBPF:一款基于eBPF的内核利用和Rootkit检测工具
关于VED-eBPF VED-eBPF是一款功能强大的内核漏洞利用和Rootkit检测工具,该工具基于eBPF技术实现其功能,可以实现Linux操作系统运行时内核安全监控和漏洞利用检测。 eBPF是一个内核内虚拟机,它允许我们直接在内核中执行代码,而无…...

配置ARM交叉编译工具的通用步骤
ARM交叉编译工具是用于编译在ARM架构上运行的代码的工具。这些工具允许开发者在一种架构(通常是x86或x64)上编写和编译代码,然后将其移植到ARM架构上运行。 ARM交叉编译工具链通常包括编译器、链接器、调试器和其他必要的工具,用…...

相机图像质量研究(5)常见问题总结:光学结构对成像的影响--景深
系列文章目录 相机图像质量研究(1)Camera成像流程介绍 相机图像质量研究(2)ISP专用平台调优介绍 相机图像质量研究(3)图像质量测试介绍 相机图像质量研究(4)常见问题总结:光学结构对成像的影响--焦距 相机图像质量研究(5)常见问题总结:光学结构对成…...

使用django构建一个多级评论功能
,评论系统是交流和反馈的重要工具,尤其是多级评论系统,它允许用户回复特定评论,形成丰富的对话结构。这个文章是使用Django框架从零开始构建一个多级评论系统。Django是一个高级Python Web框架,它鼓励快速开发和干净、…...

测试管理_利用python连接禅道数据库并自动统计bug数据到钉钉群
测试管理_利用python连接禅道数据库并统计bug数据到钉钉 这篇不多赘述,直接上代码文件。 另文章基础参考博文:参考博文 加以我自己的需求优化而成。 统计的前提 以下代码统计的前提是禅道的提bug流程应规范化 bug未解决不删除bug未关闭不删除 db_…...
Python 小白的 Leetcode Daily Challenge 刷题计划 - 20240209(除夕)
368. Largest Divisible Subset 难度:Medium 动态规划 方案还原 Yesterdays Daily Challenge can be reduced to the problem of shortest path in an unweighted graph while todays daily challenge can be reduced to the problem of longest path in an unwe…...

BFS——双向广搜+A—star
有时候从一个点能扩展出来的情况很多,这样几层之后搜索空间就很大了,我们采用从两端同时进行搜索的策略,压缩搜索空间。 190. 字串变换(190. 字串变换 - AcWing题库) 思路:这题因为变化规则很多,所以我们一层一层往外…...
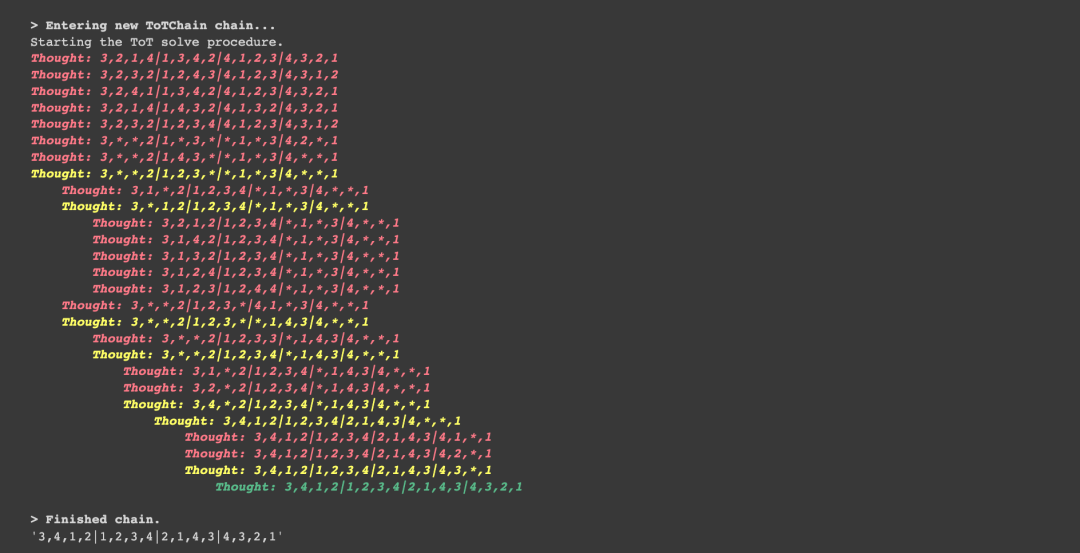
LLM之LangChain(七)| 使用LangChain,LangSmith实现Prompt工程ToT
如下图所示,LLM仍然是自治代理的backbone,可以通过给LLM增加以下模块来增强LLM功能: Prompter AgentChecker ModuleMemory moduleToT controller 当解决具体问题时,这些模块与LLM进行多轮对话。这是基于LLM的自治代理的典型情况,…...

新零售的升维体验,摸索华为云GaussDB如何实现数据赋能
新零售商业模式 商业模式通常是由客户价值、企业资源和能力、盈利方式三个方面构成。其最主要的用途是为实现客户价值最大化。 商业模式通过把能使企业运行的内外各要素整合起来,从而形成一个完整的、高效率的、具有独特核心竞争力的运行系统,并通过最…...
vscode +git +gitee 文件管理
文章目录 前言一、gitee是什么?2. Gitee与VScode连接大概步骤 二、在vscode中安装git1.安装git2.安装过程3.安装完后记得重启 三、使用1.新建文件夹first2.vscode 使用 四、连接git1.初始化仓库2.设置git 提交用户和邮箱3.登陆gitee账号新建仓库没有的自己注册一个4…...

【力扣】用栈判断有效的括号
有效的括号原题地址 方法一:栈 对于特殊情况,当字符串的长度为奇数时,一定不是有效的括号。 对于一般情况,考虑使用数据结构栈。 遍历字符串, 遇到左括号时,就入栈。遇到右括号时, 若栈顶元…...
)
【目录】CSAPP的实验简介与解法总结(已包含Attack/Link/Architecture/Cache)
文章目录 Attack Lab(缓冲区溢出实验)对应书上Chap3Link Lab(链接实验) 对应书上Chap7Architecture Lab(体系结构实验)对应书上Chap4-5Cache Lab(缓存实验)对应书上Chap6 Attack Lab…...

【机器学习】数据清洗之识别缺失点
🎈个人主页:甜美的江 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:机器学习 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、交流进步…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...
