BFS——双向广搜+A—star
有时候从一个点能扩展出来的情况很多,这样几层之后搜索空间就很大了,我们采用从两端同时进行搜索的策略,压缩搜索空间。
190. 字串变换(190. 字串变换 - AcWing题库)


思路:这题因为变化规则很多,所以我们一层一层往外扩展的时候,扩展几层后空间就会变得很大 ,那么就需要换一个思路,我们这里采用双向广搜,从两个方向来进行搜索,具体执行的时候,肯定得先从一个方向开始,那么从哪里开始呢?显然要从状态少的方向开始,我们就比较两个队列,从小的那个队列开始,然后又有新问题了,如果从一个方向开始,什么时候判停去找下一个方向,显然我们可以只往外扩展一层,扩展结束,或者两者头尾交汇的时候停止。
现在理一下我们需要哪些数据结构,首先得有两个队列分别记录从头搜索和从尾搜索的队列,另外要有两个数据结构来记录每个状态从头和从尾更新到它们时的距离。另外还要记录一下变换规则。
还有就是我们每次只往外扩展一层,所以有交汇和不交汇两种情况,如果交汇的话,那么我们可以直接返回从头到这个点和从尾到这个点的步数和,如果这个值小于10,那么显然就是最小距离,因为我们每次只从头或者从尾往外扩展一层,下次扩展时找到的,一定比当前扩展找到的多一步。当然也可能不交汇,因为我们只往外扩展一层,不交汇的时候返回一个大于10的数即可。同时我们每一次往外扩展都要记录步数,当步数大于10的时候直接停下。因为题目要求的上限就是10步。
对了如果想把两个扩展函数写在一起,一定要传入它们的更新规则,两者的扩展规则是不一样的。
#include<bits/stdc++.h>
using namespace std;
string a[10],b[10];
int n;
int expend(queue<string>&q,unordered_map<string,int>&dl,unordered_map<string,int>&dr,string a[],string b[])
{int d=dl[q.front()];while(q.size()&&dl[q.front()]==d){auto t=q.front();//cout<<t<<endl;q.pop();for(int i=0;i<n;i++){for(int j=0;j<t.size();j++){if(t.substr(j,a[i].size())==a[i]){string tmp=t.substr(0,j)+b[i]+t.substr(j+a[i].size());if(dr.count(tmp)) return dl[t]+dr[tmp]+1;if(dl.count(tmp)) continue;q.push(tmp);dl[tmp]=dl[t]+1;}}}}return 11;
}
int bfs(string s,string e)
{if(s==e) return 0;queue<string>ql,qr;unordered_map<string,int>dl,dr;ql.push(s),qr.push(e);dl[s]=dr[e]=0;int step=0;while(ql.size()&&qr.size()){int t;if(ql.size()<qr.size()) t=expend(ql,dl,dr,a,b);else t=expend(qr,dr,dl,b,a);if(t<=10) return t;if(++step>=10) return -1;}return -1;
}
int main()
{string s,e;cin>>s>>e;n=0;while(cin>>a[n]>>b[n])n++;int ans=bfs(s,e);if(ans==-1) cout<<"NO ANSWER!";else cout<<ans;
}另外这里补充一下substr()的用法:
形式 : s.substr(pos, len)
返回值: string,包含s中从pos开始的len个字符的拷贝(pos的默认值是0,len的默认值是s.size() - pos,即不加参数会默认拷贝整个s)
异常 :若pos的值超过了string的大小,则substr函数会抛出一个out_of_range异常;若pos+n的值超过了string的大小,则substr会调整n的值,只拷贝到string的末尾参考链接:C++中substr()函数用法详解_substr c++-CSDN博客
A—star算法
A—star算法也是对搜索空间进行压缩进而优化搜索。这里我们选择下一个搜索位置的时候,并不是根据它们到起点的位置来选择的,而是根据它们到起点的位置+到终点的预估值来进行选择,可以这么来理解,我们之前的bfs都是假设到终点的预估值为0,那么直接放入队列即可,这里需要用到优先队列,将从起点搜到的实际距离+到终点预估距离作为权重,放入优先队列。而预估距离要满足的条件就是小于真实距离,而且要是答案有解的情况下才能使用这个算法,否则不如bfs。
而且可以证明终点第一次出队的时候是得到的距离是最小距离。
参考链接:
AcWing 178. 第K短路(A* 反向计算最短路作为到终点的估计值) - AcWing
178. 第K短路(178. 第K短路 - AcWing题库)

思路:这道题要求起点到终点的第k短路,我们已知终点第一次出队的时候是最短路,那么第二次出队就是第儿短路,因为这条路径是被其他点更新了放进队列的,以此类推,我们只要获得终点第k次出队时的距离则可以得到答案。
然后问题就是这里的预估距离该怎么处理,因为终点固定,所以我们可以用dijkstra算法计算各点到终点的距离作为预估距离。因为它满足小于等于真实距离的条件,所以符合作为预估距离的要求。
#include<bits/stdc++.h>
using namespace std;
const int N=1010,M=20010;
typedef pair<int,int> pii;
typedef pair<int,pii> piii;
int n,m;
int rh[N],h[N],e[M],ne[M],w[M],idx;
int s,t,k;
int d[N],st[N];
void add(int h[],int a,int b,int c)
{w[idx]=c,e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dijkstra()
{memset(d,0x3f,sizeof d);d[t]=0;priority_queue<pii, vector<pii>, greater<pii>> q;q.push({0,t});while(q.size()){auto it=q.top();q.pop();int dist=it.first,v=it.second;if(st[v]) continue;st[v]=1;for(int i=rh[v];i!=-1;i=ne[i]){int j=e[i];if(d[j]>dist+w[i]){d[j]=dist+w[i];q.push({d[j],j});}}}
}
int cnt[N];
int bfs()
{priority_queue<piii, vector<piii>, greater<piii>> q;q.push({d[s],{0,s}});while(q.size()){auto it=q.top();q.pop();int dist=it.second.first,v=it.second.second;cnt[v]++;if(v==t&&cnt[v]==k) return dist;for(int i=h[v];i!=-1;i=ne[i]){int j=e[i];if(cnt[j]<k)q.push({dist+w[i]+d[j],{dist+w[i],j}});}}return -1;
}
int main()
{memset(h,-1,sizeof h);memset(rh,-1,sizeof rh);scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){int a,b,c;scanf("%d%d%d",&a,&b,&c);add(h,a,b,c);add(rh,b,a,c);}scanf("%d%d%d",&s,&t,&k);if(s==t) k++;//因为最初s就会被放进去,每条最短路中至少要包含一条边。dijkstra();cout<<bfs();
}179. 八数码(179. 八数码 - AcWing题库)


这题是将棋盘整个视为一种状态,我们每一个点最多只能扩展出四种状态,我们可以用之前魔板那道题的写法,稍微变一下,变成双向广搜,自然也可以用A—star算法,因为状态还是有些许多。
A—star算法需要保证有解,那么我们就提前预判一下是否有解,如果有解再去进行查找。
八数码问题有个预判的技巧,我们按行读入数字,得到的一个数组中,如果逆序对的数量为奇数,那么就无解,如果逆序对的数量为偶数,那么就有解。

可以这么来理解,如果我们在行内进行移动,实际上并没有改变序列,也就是并未改变逆序对数量,如果在行与行之间进行移动,那么相当于只改变了它前面或者后面两个数的位置,我们以一种情况为例,它实际上就只改变了3个数内部的相对顺序,所以实际上逆序对的数量要么不变要么就多2或者少2,所以起始状态和结束状态中逆序对的奇偶性相同,我们可以顺序排列的时候逆序对的数量是0,那么起始状态中逆序对的数量应该是偶数。
然后就是考虑估价函数,我们计算出每个数当前位置和目标位置的曼哈顿距离,很显然,每次移动最好的情况只会让一个数和它的实际位置的曼哈顿距离减1,所以我们可以将每个状态中每个数当前位置与目标位置的曼哈顿距离和算出来,作为预估距离。
#include<bits/stdc++.h>
using namespace std;
string s,e;
char a[4][4];
unordered_map<string,int>d;
unordered_map<string,pair<string,char>>pre;
char op[]={'u','d','l','r'};//x的位置
void toa(string t)
{for(int i=0;i<t.size();i++){a[i/3][i%3]=t[i];}
}
string tos()
{string res="";for(int i=0;i<3;i++)for(int j=0;j<3;j++)res += a[i][j];return res;
}
string move0(string t)//u
{toa(t);int x,y;for(int i=0;i<3;i++)for(int j=0;j<3;j++)if(a[i][j]=='x') x=i,y=j;if(x!=0){swap(a[x][y],a[x-1][y]);}return tos();
}
string move1(string t)//d
{toa(t);int x,y;for(int i=0;i<3;i++)for(int j=0;j<3;j++)if(a[i][j]=='x') x=i,y=j;if(x!=2){swap(a[x][y],a[x+1][y]);}return tos();
}
string move2(string t)//l
{toa(t);int x,y;for(int i=0;i<3;i++)for(int j=0;j<3;j++)if(a[i][j]=='x') x=i,y=j;if(y!=0){swap(a[x][y],a[x][y-1]);}return tos();
}
string move3(string t)//r
{toa(t);int x,y;for(int i=0;i<3;i++)for(int j=0;j<3;j++)if(a[i][j]=='x') x=i,y=j;if(y!=2){swap(a[x][y],a[x][y+1]);}return tos();
}
typedef pair<int,pair<int,string>> piis;
int tj(string g)
{int cnt=0;//逆序对数量for(int i=0;i<g.size();i++){for(int j=i+1;j<g.size();j++){if(g[i]>g[j]) cnt++;}}return cnt;
}
void bfs()
{priority_queue<piis,vector<piis>,greater<piis>>q;int cnt=tj(s);q.push({cnt,{0,s}});d[s]=0;if(s==e) return;while(q.size()){auto t=q.top();q.pop();string tv=t.second.second;int dist=t.second.first;// cout<<tv<<endl;string tmp[5];tmp[0]=move0(tv);tmp[1]=move1(tv);tmp[2]=move2(tv);tmp[3]=move3(tv);for(int i=0;i<4;i++){// cout<<tmp[i]<<endl;if(d.count(tmp[i])) continue;d[tmp[i]]=dist+1;pre[tmp[i]]={tv,op[i]};cnt=tj(tmp[i]);q.push({cnt+d[tmp[i]],{d[tmp[i]],tmp[i]}});if(tmp[i]==e) return;}//cout<<endl;}
}
int main()
{string g="";char c;while(cin>>c)//不会录入空格{s += c;if(c!='x') g+=c;}e="12345678x";int cnt=0;//逆序对数量for(int i=0;i<g.size();i++){for(int j=i+1;j<g.size();j++){if(g[i]>g[j]) cnt++;}}if(cnt%2) cout<<"unsolvable";else{bfs();//cout<<d[e]<<endl;if(d[e]){string res="";while(e!=s){res += pre[e].second;e=pre[e].first;}reverse(res.begin(),res.end());cout<<res;}}
}ps:代码看似复杂,但复用率极高,只要把逻辑盘清楚,实际上并不麻烦。
总的来说,A—star可以提高效率,但是估价函数一定要写明白。
另外补充一点,cin录单个字符的时候不会把空格录进去,如果没有更好的方法避免空格的话,可以用cin。
相关文章:

BFS——双向广搜+A—star
有时候从一个点能扩展出来的情况很多,这样几层之后搜索空间就很大了,我们采用从两端同时进行搜索的策略,压缩搜索空间。 190. 字串变换(190. 字串变换 - AcWing题库) 思路:这题因为变化规则很多,所以我们一层一层往外…...
LLM之LangChain(七)| 使用LangChain,LangSmith实现Prompt工程ToT
如下图所示,LLM仍然是自治代理的backbone,可以通过给LLM增加以下模块来增强LLM功能: Prompter AgentChecker ModuleMemory moduleToT controller 当解决具体问题时,这些模块与LLM进行多轮对话。这是基于LLM的自治代理的典型情况,…...

新零售的升维体验,摸索华为云GaussDB如何实现数据赋能
新零售商业模式 商业模式通常是由客户价值、企业资源和能力、盈利方式三个方面构成。其最主要的用途是为实现客户价值最大化。 商业模式通过把能使企业运行的内外各要素整合起来,从而形成一个完整的、高效率的、具有独特核心竞争力的运行系统,并通过最…...
vscode +git +gitee 文件管理
文章目录 前言一、gitee是什么?2. Gitee与VScode连接大概步骤 二、在vscode中安装git1.安装git2.安装过程3.安装完后记得重启 三、使用1.新建文件夹first2.vscode 使用 四、连接git1.初始化仓库2.设置git 提交用户和邮箱3.登陆gitee账号新建仓库没有的自己注册一个4…...

【力扣】用栈判断有效的括号
有效的括号原题地址 方法一:栈 对于特殊情况,当字符串的长度为奇数时,一定不是有效的括号。 对于一般情况,考虑使用数据结构栈。 遍历字符串, 遇到左括号时,就入栈。遇到右括号时, 若栈顶元…...
)
【目录】CSAPP的实验简介与解法总结(已包含Attack/Link/Architecture/Cache)
文章目录 Attack Lab(缓冲区溢出实验)对应书上Chap3Link Lab(链接实验) 对应书上Chap7Architecture Lab(体系结构实验)对应书上Chap4-5Cache Lab(缓存实验)对应书上Chap6 Attack Lab…...

【机器学习】数据清洗之识别缺失点
🎈个人主页:甜美的江 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:机器学习 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、交流进步…...
【Vue】Vue基础入门
📝个人主页:五敷有你 🔥系列专栏:Vue ⛺️稳重求进,晒太阳 Vue概念 是一个用于构建用户界面的渐进式框架优点:大大提高开发效率缺点:需要理解记忆规则 创建Vue实例 步骤: …...
正点原子-STM32通用定时器学习笔记(1)
目录 1. 通用定时器简介(F1为例) 2. 通用定时器框图 ①时钟源 ②控制器 ③时基单元 ④输入捕获 ⑤捕获/比较(公共) ⑥输出比较 3.时钟源配置 3.1 计数器时钟源寄存器设置方法 3.2 外部时钟模式1 3.3 外部时钟模式2 3…...
Redis篇之redis是单线程
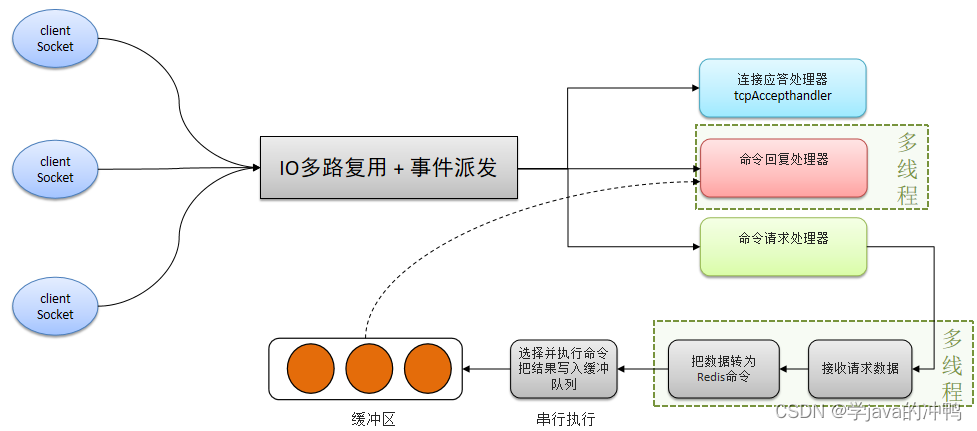
一、redis是单线程 Redis是单线程的,但是为什么还那么快?主要原因有下面3点原因: 1. Redis是纯内存操作,执行速度非常快。 2. 采用单线程,避免不必要的上下文切换可竞争条件,多线程还要考虑线程安全问题。 …...

随机MM引流源码PHP开源版
引流源码最新随机MM开源版PHP源码,非常简洁好看的单页全解代码没任何加密 直接上传即可用无需数据库支持主机空间...

【C++修行之道】(引用、函数提高)
目录 一、引用 1.1引用的基本使用 1.2 引用注意事项 1.3 引用做函数参数 1.4 引用做函数返回值 1.5 引用的本质 1.6 常量引用 1.7引用和指针的区别 二、函数提高 2.1 函数默认参数 2.2函数占位参数 2.3 函数重载 2.4函数重载注意事项 一、引用 1.1引用的基本使用 …...
从零开始手写mmo游戏从框架到爆炸(十一)— 注册与登录
导航:从零开始手写mmo游戏从框架到爆炸(零)—— 导航-CSDN博客 从这一章开始,我们进入业务的部分,从注册登录开始。 创建注册和登录的路由 package com.loveprogrammer.command.server;public interface Se…...

【SpringBoot】Redis集中管理Session和自定义用户参数解决登录状态及校验问题
🏡浩泽学编程:个人主页 🔥 推荐专栏:《深入浅出SpringBoot》《java对AI的调用开发》 《RabbitMQ》《Spring》《SpringMVC》 🛸学无止境,不骄不躁,知行合一 文章目录 前言一、分布…...
(二))
【0256】揭晓pg内核中MyBackendId的分配机制(后端进程Id,BackendId)(二)
上一篇:【0255】揭晓pg内核中MyBackendId的分配机制(后端进程Id,BackendId)(一) 文章目录 1. 前言2. 分配BackendId2.1 何时为backend process分配BackendId2.1.1 找出未使用的slot(inactive slot)2.3 BackendId序号从多少开始?2.4 后端进程退出后,其BackendId被释放…...

eclipse4.28.0版本如何安装FatJar插件
场景: 今天准备温故下以前的老项目,于是下载了最新版本的Eclipse IDE for Enterprise Java and Web Developers - 2023-06,老项目中有些需要将程序打成jar包,于是考虑安装FatJar插件。 问题描述 一顿操作后,发现FatJar死活安装了,在线安装提示content.xml异常;离线安装…...

查大数据检测到风险等级太高是怎么回事?
随着金融风控越来越多元化,大数据作为新兴的技术被运用到贷前风控中去了,不少人也了解过自己的大数据,但是由于相关知识不足,看不懂报告,在常见的问题中,大数据检测到风险等级太高是怎么回事呢?小易大数据…...

Leetcode 30天高效刷数据结构和算法 Day1 两数之和 —— 无序数组
两数之和 —— 无序数组 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现…...

Hair Tool for Blender3D
CGer.com - Hair Tool for Blender3D - CGer资源网 Hair Tool 1.5 for Blender3D 链接: https://pan.baidu.com/s/1kVABn6n 密码: gwprHair Tool 1.65-1.8 for Blender链接: https://pan.baidu.com/s/1A7cW_Ms2baGQ2M0iE1dQhQ 密码: 81bqHair Tool for Blender 1.9.2链接: http…...

【最详解】如何进行点云的凹凸缺陷检测(opene3D)(完成度80%)
文章目录 前言实现思路想法1想法2想法3 补充实现想法1想法2代码 想法3代码 总结 前言 读前须知: 首先我们得确保你已经完全知晓相关的基本的数学知识,其中包括用最小二乘法拟合曲二次曲面,以及曲面的曲率详细求解。若还是没弄清楚࿰…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...
