2024年刘谦魔术大揭秘,其中竟用到了约瑟夫环?
目录
前言
魔术过程
揭秘过程
结尾
前言
不知道昨天春晚时刘谦的魔术大家看了没有,相信大家跟我一样也很疑惑,所以爆肝一天我得出了结论。如果你觉得还不错的话,记得点赞收藏,分享给更多的朋友看。
魔术过程
整个魔术可以分成十步,你可以学一学变给同学看,他们一定会震惊十万年的。
1.任意选四张牌,并把牌洗混。
2.把扑克牌对折后撕开,让一堆放在另一堆上面,合并成8张牌。
3.名字有几个字就把扑克牌从上面往下挪动几张。
4.拿出最上面的三张牌,插入剩下牌的中间(位置随意)。
5.把最上面的牌拿走放在口袋里。
6.按照南北方人拿出不同的数量插入中间(南1北2不知道3)。
7.按性别分别丢弃最上面的牌(男1女2)。
8.嘴里喊出“见证奇迹的时刻”,每喊一个字,把一张牌从上面拿到最下面。
9.“好运留下来,烦恼丢出去”,当喊出“好运留下来”时,把最上面的牌拿到最底下;当喊出“烦恼丢出去”时,把最上面的牌丢出去(扔掉),重复步骤知道剩余一张牌。
10.如果你步骤正确的话,剩余的半张牌和放在口袋里的半张牌会正好拼成一张牌。
揭秘过程
我们逐个步骤来看。
1.任意选四张牌,并把牌洗混。
表面上看是每个人都不一样,很随机,但是你忽略了一点,他最终不是猜你的牌,而是让你手中的两张牌配对起来,所以再怎么打乱,人人都一样,属于障眼法。
2.把扑克牌对折后撕开,让一堆放在另一堆上面,合并成8张牌。
我们把这8张牌设为:ABCD abcd
一堆放在另一堆上面,并没有改变ABCD的顺序。
进一步观察,发现任意两张配对的牌之间都间隔3张牌。
3.名字有几个字就把扑克牌从上面往下挪动几张。
表面上看是把牌堆又弄乱了,但你仔细想一想,不管你移动多少张,两张配对的牌始终间隔3张牌。如下面的例子:
张三:ABCDabcd→CDabcdAB
王小明:ABCDabcd→DabcdABC
所以这一步属于障眼法。
4.拿出最上面的三张牌,插入剩下牌的中间(位置随意)。
这一步非常关键,观察牌堆,如果我们把上面三张插入中间,顶牌和底牌已经配对了。
张三:ABCDabcd→CDabcdAB→bCDacdAB(不管怎样插,头尾都会配对)
王小明:ABCDabcd→DabcdABC→cdDabABC
5.把最上面的牌拿走放在口袋里。
这一步把顶牌拿走,也就是说此时此刻需要配对的牌是底牌。
6.按照南北方人拿出不同的数量插入中间(南1北2不知道3)。
你插来插去,底牌还是没有变,属于障眼法。
7.按性别分别丢弃最上面的牌(男1女2)。
你丢来丢去,底牌还是没有变,属于障眼法。
8.嘴里喊出“见证奇迹的时刻”,每喊一个字,把一张牌从上面拿到最下面。
这一步需要模拟一下,因为底牌顺序完全改变了。
张三(BOY):ABCDabcd→CDabcdAB→bCDacdAB→DacdAB→acdABD
王小明(GRIL):ABCDabcd→DabcdABC→cdDabABC→abABC→ABCab
9.“好运留下来,烦恼丢出去”,当喊出“好运留下来”时,把最上面的牌拿到最底下;当喊出“烦恼丢出去”时,把最上面的牌丢出去(扔掉),重复步骤知道剩余一张牌。
重中之重,约瑟夫问题!
我们可以写一个程序来验证一下,有几张牌相当于有几个人报数,报2淘汰。
#include<bits/stdc++.h> using namespace std; int main() {int n;cin>>n;int a[n+1]={0};for(int i=1;i<=n;i++) a[i]=i; int num=n;//num为剩余人数 int count=1;//count为当前要报的数字 int tmp=0;//tmp为当前该哪个位置报数了 int l=1;//l表示当前是第几轮 while(num!=0) {tmp++;if(tmp>n) tmp=1;if(a[tmp]!=-1){if(count==2){cout<<a[tmp]<<" ";a[tmp]=-1;num--; count=0;}count++;}}return 0; }张三:
出圈顺序:2 4 6 3 1 5
5对应字符串“acdABD”里的B。
王小明:
出圈顺序:2 4 1 5 33对应字符串“ABCab”里的C。
这一步多理解理解,魔术精髓就在这。
10.如果你步骤正确的话,剩余的半张牌和放在口袋里的半张牌会正好拼成一张牌。
神奇是神奇,但是被我揭穿了,哈哈哈。
结尾
怎么样,你学会了吗?制作不易,希望点个赞评个论再走。
我看了看写满了的草稿纸,你确定不点个关注吗?
我是爱证明的小芒果,我们下次再见,Happy Chinese New Year!
相关文章:

2024年刘谦魔术大揭秘,其中竟用到了约瑟夫环?
目录 前言 魔术过程 揭秘过程 结尾 前言 不知道昨天春晚时刘谦的魔术大家看了没有,相信大家跟我一样也很疑惑,所以爆肝一天我得出了结论。如果你觉得还不错的话,记得点赞收藏,分享给更多的朋友看。 魔术过程 整个魔术可以分…...

openssl3.2 - update debian12‘s default openssl to openssl3.2
文章目录 openssl3.2 - update debian12s default openssl to openssl3.2概述笔记回到debian12自带的openssl版本从源码编译安装最新版的openssl配置ssl访问END openssl3.2 - update debian12’s default openssl to openssl3.2 概述 在debian12虚拟机中编译了openssl3.2(ope…...

VUE2和VUE3区别对比一览
## Vue3总结 ### 官方文档 * [Vue3](https://v3.cn.vuejs.org/api/options*data.html) * [Vue2](https://vuejs.bootcss.com/api/) ### Vue3相对于Vue2的语法特性#### 1.获取数据 * vue2 javascript export default {data() {return {name: myName,}},mounted() {console.log(t…...

Linux - updatedb 命令
1. 功能 updatedb 命令用来创建或更新slocate命令所必需的数据库文件。updatedb 命令的执行过程较长,因为在执行时它会遍历整个系统的目录树,并将所有的文件信息写入 slocate 数据库文件中。 补充说明:slocate 本身具有一个数据库ÿ…...

云计算市场分析
目录 一、云计算市场概述 1.1 概述 二、国外云计算厂商 2.1 亚马逊AWS 2.2 微软AzureAzure 2.3 Apple iCloud 三、国内云计算厂商 3.1 阿里云 3.2 腾讯云 3.3 华为云 3.4 百度智能云 一、云计算市场概述 1.1 概述 云计算从出现以来,其发展就非常迅速。以…...
前端JavaScript篇之call() 和 apply() 的区别?
目录 call() 和 apply() 的区别? call() 和 apply() 的区别? 在JavaScript中,call()和apply()都是用来改变函数中this指向的方法,它们的作用是一样的,只是传参的方式不同。 call()方法和apply()方法的第一个参数都是…...
)
Java设计模式大全:23种常见的设计模式详解(三)
本系列文章简介: 设计模式是在软件开发过程中,经过实践和总结得到的一套解决特定问题的可复用的模板。它是一种在特定情境中经过验证的经验和技巧的集合,可以帮助开发人员设计出高效、可维护、可扩展和可复用的软件系统。设计模式提供了一种在设计和编码过程中的指导,它用于…...
十六位汇编框架、子程序与堆栈)
汇编语言程序设计(二)十六位汇编框架、子程序与堆栈
寄存器 如下是16位通用寄存器,存储在cpu硬件中 AX 返回值 AX寄存器分为两部分 AH和AL AH 高8位 存储功能号 AL 低8位 存储返回码 以下是一个AX寄存器应用: mov ax,4c00h 4c给高位AL,00低位AL,16进制要以h结尾 BX CX 计数…...
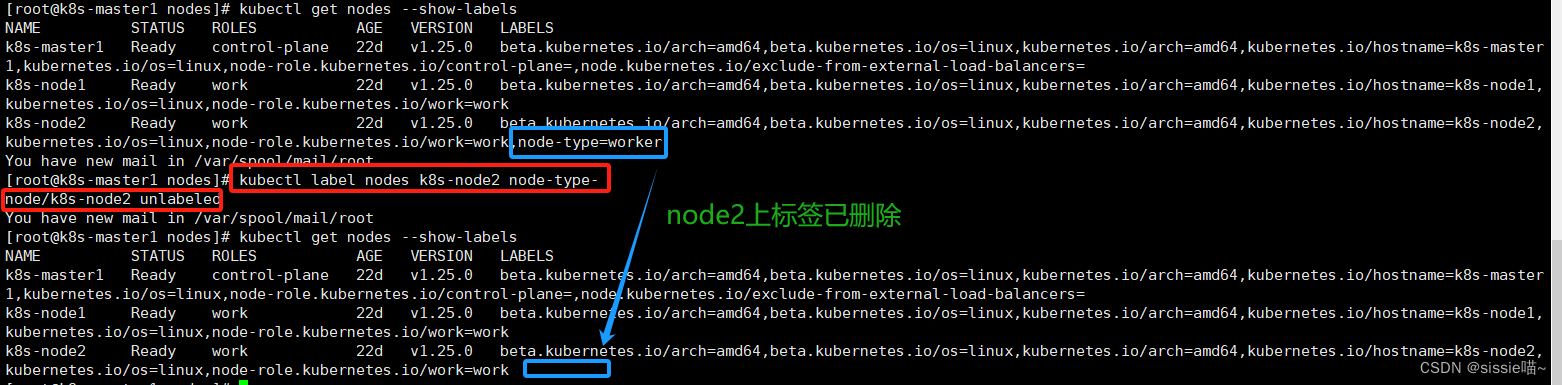
K8S之标签的介绍和使用
标签 标签定义标签实操1、对Node节点打标签2、对Pod资源打标签查看资源标签删除资源标签 标签定义 标签就是一对 key/value ,被关联到对象上。 标签的使用让我们能够表示出对象的特点,比如使用在Pod上,能一眼看出这个Pod是干什么的。也可以用…...

网络请求库axios
一、认识Axios库 为什么选择axios? 功能特点: 在浏览器中发送 XMLHttpRequests 请求在 node.js 中发送 http请求支持 Promise API拦截请求和响应转换请求和响应数据 补充: axios名称的由来? 个人理解没有具体的翻译. axios: ajax i/o system 二、axios发送请求 1.axios请求…...

程序设计语言的组成
程序设计语言的组成 程序设计语言基本上由数据、运算、控制、传输组成 数据成分 数据是程序操作的对象,具有存储类别、类型、名称、作用域和生存期等属性 从不同角度可将数据进行不同的划分。 数据类型的分类如下: 按程序运行过程中数据的值能否改…...

论文精读的markdown模板——以及用obsidian阅读网页资料做笔记
# The Investigation of S-P Chart Analysis on the Test Evaluations of Equality Axiom Concepts for Sixth Graders Tags: #/unread 本体论: 背景起源和发展 包含要素 # # # 可关联要素 # # # 逻辑 意义: 方法论: 方法论是一…...

LCP 30. 魔塔游戏
LCP 30. 魔塔游戏 难度: 中等 题目: 小扣当前位于魔塔游戏第一层,共有 N 个房间,编号为 0 ~ N-1。每个房间的补血道具/怪物对于血量影响记于数组 nums,其中正数表示道具补血数值,即血量增加对应数值;负数表示怪物造…...

RCE(命令执行)知识点总结最详细
description: 这里是CTF做题时常见的会遇见的RCE的漏洞知识点总结。 如果你觉得写得好并且想看更多web知识的话可以去gitbook.22kaka.fun去看,上面是我写的一本关于web学习的一个gitbook,当然如果你能去我的github为我的这个项目点亮星星我会感激不尽htt…...

[英语学习][27][Word Power Made Easy]的精读与翻译优化
[序言] 译者的这次翻译非常好. 对what与从句的嵌套用法, 进行了精准的翻译. 这次的记录, 也是对我自己的一次翻译经验的提升. 但是唯一遗憾的是"derivation"没有翻译好. [英文学习的目标] 提升自身的英语水平, 对日后编程技能的提升有很大帮助. 希望大家…...

Jupyter Notebook如何在E盘打开
Jupyter Notebook如何在E盘打开 方法1:方法2: 首先打开Anaconda Powershell Prompt, 可以看到默认是C盘。 可以对应着自己的界面输入: 方法1: (base) PS C:\Users\bella> E: (base) PS E:\> jupyter notebook方法2&#x…...

显示器校准软件:BetterDisplay Pro for Mac v2.0.11激活版下载
BetterDisplay Pro是一款由waydabber开发的Mac平台上的显示器校准软件,可以帮助用户调整显示器的颜色和亮度,以获得更加真实、清晰和舒适的视觉体验。 软件下载: BetterDisplay Pro for Mac v2.0.11激活版下载 以下是BetterDisplay Pro的主要…...
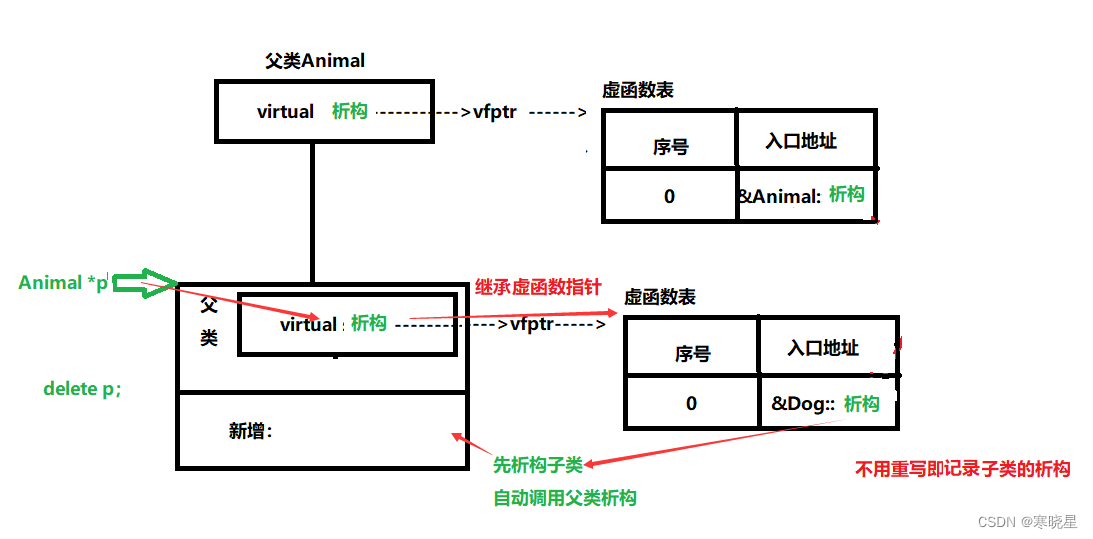
【第六天】c++虚函数多态
一、多态的概述 多态按字面的意思就是多种形态。当类之间存在层次结构,并且类之间是通过继承关联(父类与子类)时,就会用到多态。 C 多态意味着调用成员函数时,会根据调用函数的对象的类型来执行不同的函数。 静态多态&…...

CGAL::2D Arrangements-3
3.Arrangement查询 Arrangement里面最重要的查询操作是point-location,给定一个点,查找到包含这个点的Arrangement。通常情况下,point-location查询得到的结果是Arrangement的一个face,退化情况下会是一个edge,查一个…...
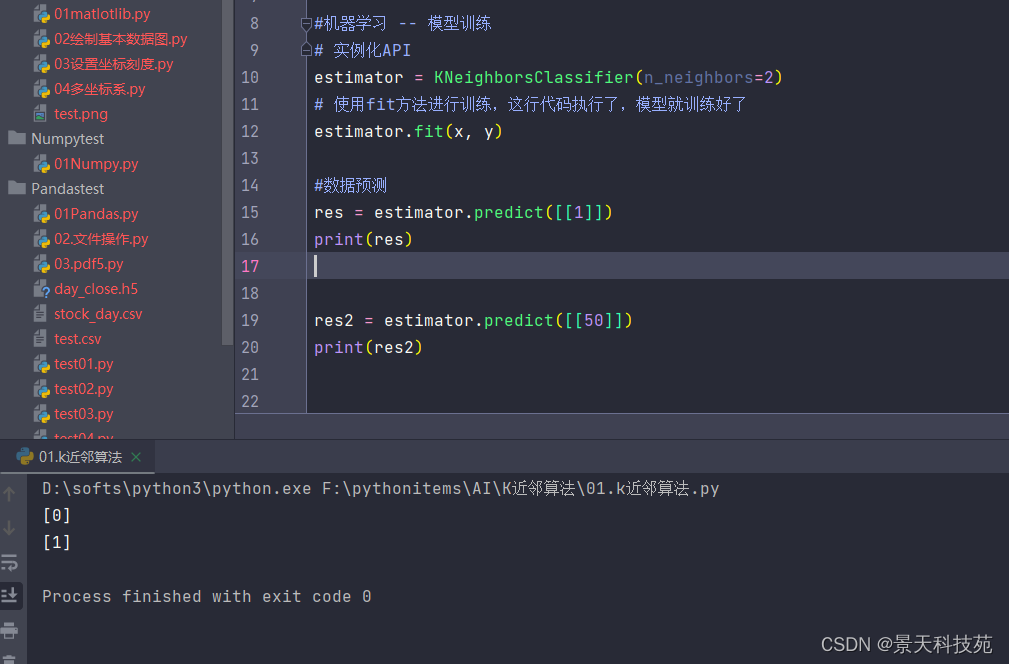
机器学习--K近邻算法,以及python中通过Scikit-learn库实现K近邻算法API使用技巧
文章目录 1.K-近邻算法思想2.K-近邻算法(KNN)概念3.电影类型分析4.KNN算法流程总结5.k近邻算法api初步使用机器学习库scikit-learn1 Scikit-learn工具介绍2.安装3.Scikit-learn包含的内容4.K-近邻算法API5.案例5.1 步骤分析5.2 代码过程 1.K-近邻算法思想 假如你有一天来到北京…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...
