MATLAB矩阵的操作(第二部分)
师从清风
矩阵的创建方法
在MATLAB中,矩阵的创建方法主要有三种,分别是:直接输入法、函数创建法和导入本地文件中的数据。
直接输入法
输入矩阵时要以中括号“[ ]”作为标识符号,矩阵的所有元素必须都在中括号内。
矩阵的同行元素之间用空格或逗号分隔,行与行之间用分号或回车键分隔。
a = [1 2 3; 4 5 6]
b = [1,2,3; 4,5,6]
c = [2 56 7]
d = [3 6;6 9] % 还可以既加分号又加回车键进行换行如果不想显示输出结果,可以在语句的最后用英文分号“;”结束。(工作区还是可以找到我们创建的矩阵)
e = [2, 35, 7];函数创建法
MATLAB提供了一些函数,这些函数可以用来生成某些特定的矩阵,我们这里介绍几个最常用到的函数。
zeros、ones和eye
这三个函数可用来分别创建全为0的矩阵、全为1的矩阵和单位矩阵。
以zeros函数为例,其常见的用法有两种:
(1)zeros(n)可以创建一个n行n列全为0的矩阵;
(2)zeros(m,n)可以创建一个m行n列全为0的矩阵。
a = zeros(3) b = zeros(2,3) c = ones(5) d = ones(1,4)
单位矩阵:主对角线元素为 1 且其他位置元素为 0 。
e = eye(4)
f = eye(4,3)
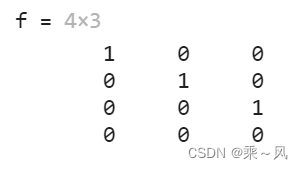
g = eye(3,4)

rand、randi和randn
这三个函数分别用来创建均匀分布的随机数、均匀分布的随机整数和标准正态分布的随机数
rand函数可用来创建区间0到1均匀分布的随机数,其最常用的方法有两种:
(1)rand(n)可以创建一个n行n列的随机数矩阵;
(2)rand(m,n)可以创建一个m行n列的随机数矩阵。
由rand函数创建的随机数矩阵的每个元素都随机取样自0和1之间的均匀分布。
rand(3) rand(3,2)
randi函数是用来创建均匀分布的随机整数(randi后的i是integer的缩写),其最一般的使用方法为:randi([imin,imax],m,n),可以用来创建一个m行n列的随机数矩阵,该随机数矩阵中的每个元素都是从区间[imin,imax]内随机抽取的整数。
例子:假设我们要模拟投掷100次骰子,骰子有6个面,那么我们可以使用randi([1,6],1,100)得到一个长度为100的行向量,向量中的每个元素都是取自1,2,3,4,5,6中的一个整数。
randi([1,6],1,100) % 这里我生成一个行向量,也可以生成列向量
另外,如果imin等于1,那么可以简写为randi(imax,m,n);
randi(6,1,100)
如果m和n相同,即生成一个n行n列的方阵,那么可以直接写成randi([imin,imax],n)。
randi([-3 3],5)
randn函数用来创建标准正态分布的随机数(randn后的n是norm distribution的缩写),其使用方法和rand函数类似:
(1)randn(n)可以创建一个n行n列的随机数矩阵;
(2)randn(m,n)可以创建一个m行n列的随机数矩阵。
注:1、由randn函数创建的随机数矩阵的每个元素都随机取样自标准正态分布。
2、标准正态分布:以0为均值、以1为标准差的正态分布,记为N(0,1).
diag和blkdiag
diag函数可用来创建对角矩阵或者获取矩阵的对角元素(diagonal 对角的)。
情况1:如果输入的第一个参数是向量,则表示创建对角矩阵。
diag(v,k) 将向量v的元素放置在第k条对角线上,其他位置元素为0。
k=0 表示主对角线,k>0 位于主对角线上方,k<0 位于主对角线下方。
如果k=0, 可以直接写成diag(v)。
diag([1,2,3]) % 或者写成diag([1,2,3], 0)
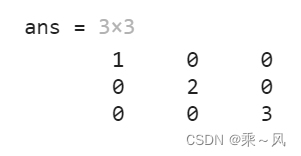
diag([1,2,3],-1)
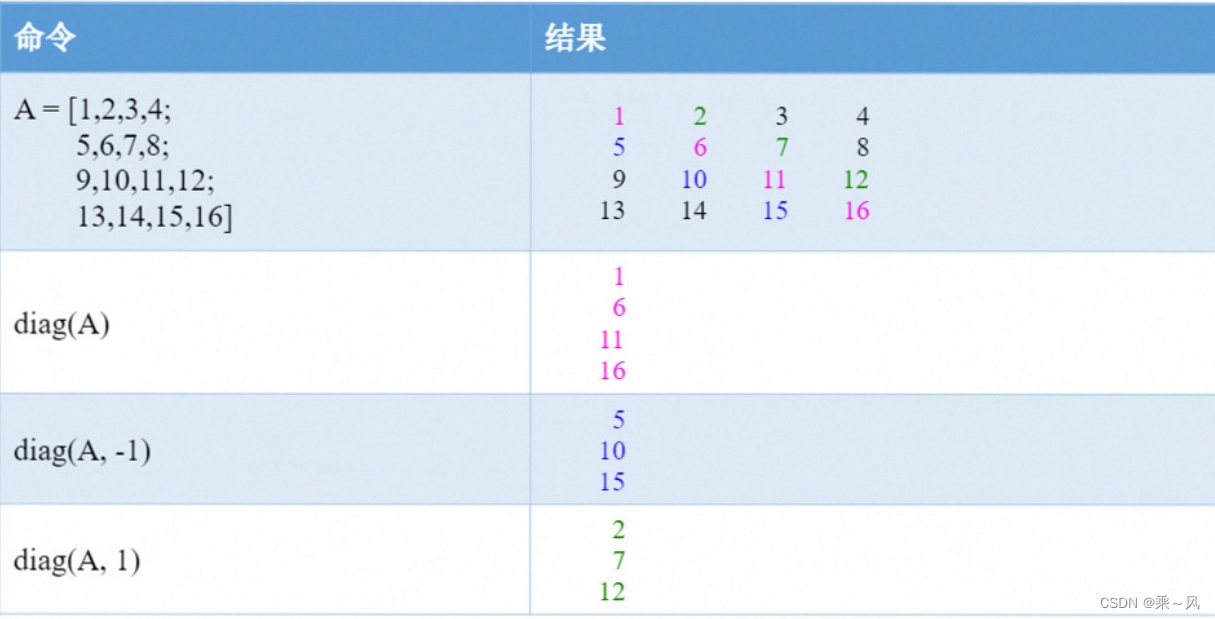
情况2:如果输入的第一个参数是矩阵,则表示获取矩阵的对角元素。
diag(A,k) 返回A的第k条对角线上元素的构成的列向量。
k表示对角线编号,我们将其指定为一个整数。
k=0 表示主对角线,k>0 位于主对角线上方,k<0 位于主对角线下方。
如果k=0, diag(A, 0)可以直接写成diag(A)。
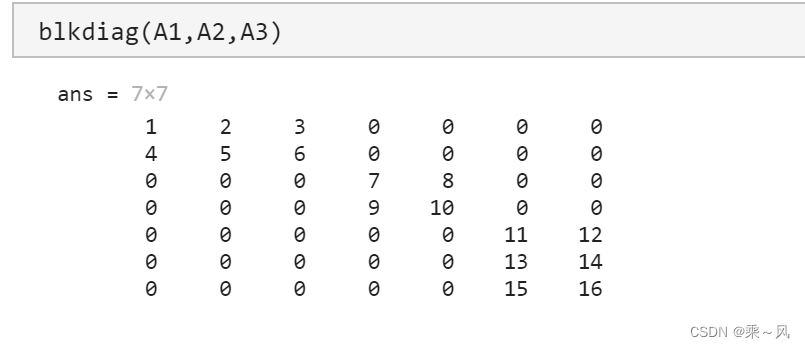
blkdiag函数可用来创建分块对角矩阵(block diagnoal 分块对角)。
分块对角矩阵是相对于常规的对角矩阵而言的,常规的对角矩阵沿对角线具有单个元素,而分块对角矩阵的对角线的元素是矩阵。
我们可采用以下形式表示一个分块对角矩阵:
A1 = [1,2,3;4,5,6]
A2 = [7,8;9,10]
A3 = [11,12;13,14;15,16]
blkdiag(A1,A2,A3)
导入本地文件中的数据
MATLAB可读取本地的文件,支持的常见格式如下:
.txt、.dat 或 .csv(适用于带分隔符的文本文件)
.xls、.xlsb、.xlsm、.xlsx、.xltm、.xltx 或 .ods(适用于电子表格文件)
矩阵元素的引用
双下标索引
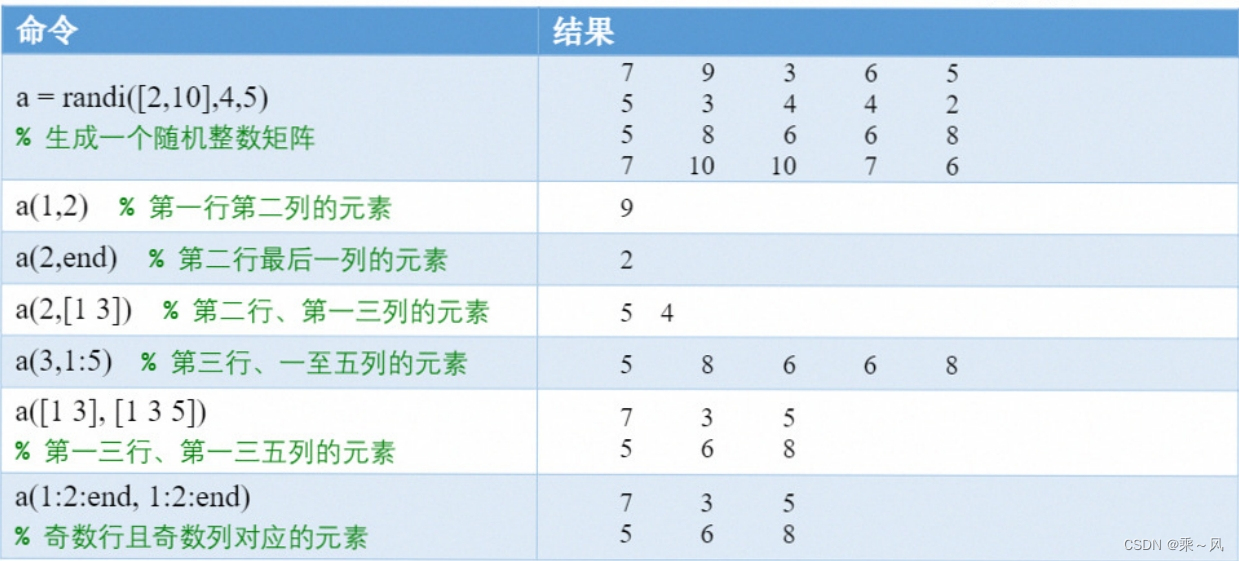
我们可以使用矩阵元素所处的行(row)和列(column)来进行引用矩阵的某一个元素,方式为:a(row_ind, column_ind).
size函数
可以使用size函数来计算矩阵的大小
有三种常见的用法:
(1)size(A) 返回一个行向量,其元素是 A 的相应维度的长度。
A = ones(4,6) % 全为1的矩阵
s = size(A) % 返回[4,6],表示有4行和6列

(2)size(A,dim)返回在维度dim上的长度。dim=1表示行;dim=2表示列
r_num = size(A,1) % 行数 r_num=4
c_num = size(A,2) % 列数 c_num=6
注意:即使A是一个向量,size(A)返回的结果也是一个向量,而不是向量的长度。
A = 1:5; % 行向量:[1 2 3 4 5]
size(A)=1 5
(3)size函数可以有两个返回值
第一个返回的元素用来保存行数;第二个返回的元素用来保存列数
A = zeros(3,5)
[r, c] = size(A) %输出 r=3 c=5
length函数和numel函数也可以用在矩阵上。
length函数会返回行和列的较大值
A = ones(3,4)
length(A)=4
numel函数会返回矩阵中元素的总数
numel(A)=3*4=12
有时候我们需要取出矩阵的某一行或者某一列。以取出矩阵A的第一行为例,我们可以使用代码A(1, 1:end),即row_ind取1表示第一行,column_ind取1:end表示从1到最后一列的索引。
A = randi([2,10],4,5)
A(1,1:end)
这时候我们可以直接将其简写为:A(1, :),逗号后面是列索引的位置,加一个冒号就表示取出每一列的元素。
A(1,:)
同理,要取第一列的所有元素,我们可以使用代码:A(:, 1)
A(:, 1)
总结:
A(:, n) 表示矩阵A的第n列的所有元素。
A(m, :) 表示矩阵A的第m行的所有元素。
线性索引(单下标)
使用单个下标对矩阵进行索引这种单下标的索引方法称为线性索引。
事实上,在MATLAB中,矩阵的数据在计算机的内存中被存储为单列。以下图为例,下面的矩阵虽然显示为 3×3 矩阵,但MATLAB在内存中将它存储为单列,由它的各列顺次连接而成。
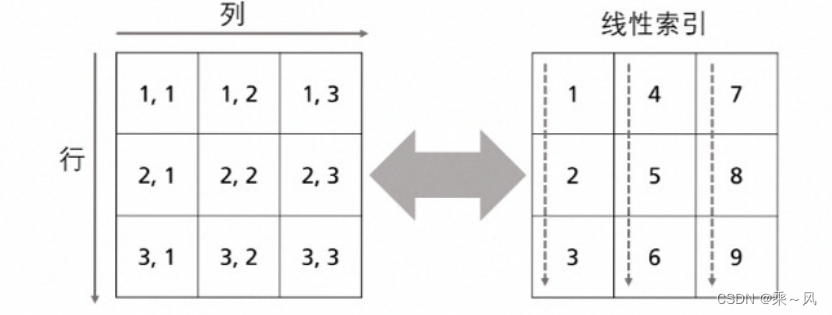
我们可以利用线性索引来取出矩阵中的元素,尽管这种方式并不那么直观。
举个例子:
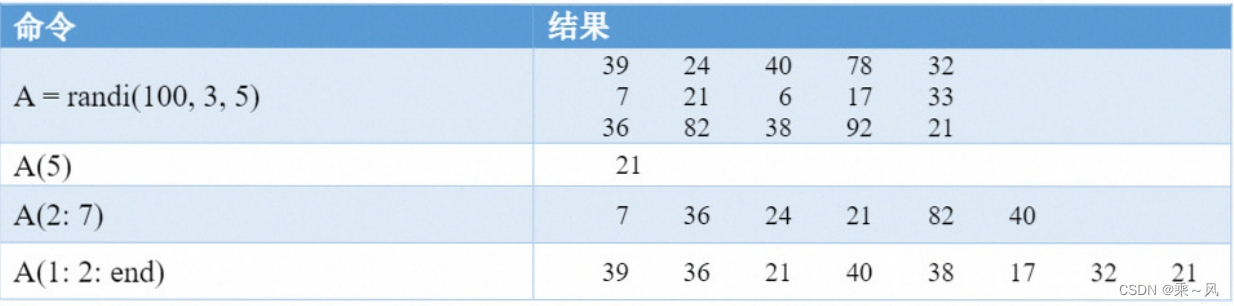
A(:)命令可以将A中的所有元素按照线性索引的方式重构成一个列向量,这个命令后面会经常用到。
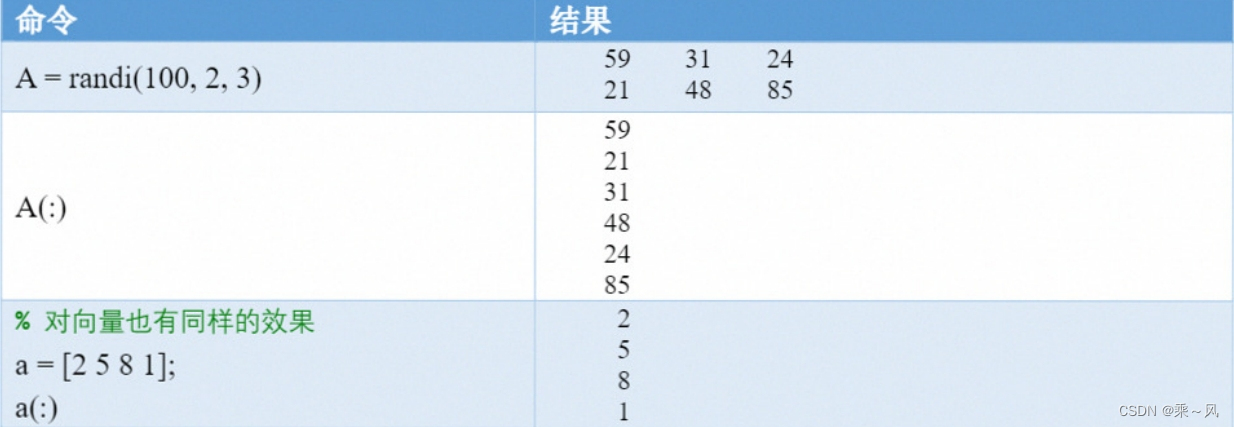
sub2ind和ind2sub函数
可用于在矩阵的原始索引(双下标)和线性索引之间进行转换(用到频率不高)(subscript 下标)。
sub2ind将矩阵的下标转换为线性索引
ind = sub2ind(sz,row,col) 针对大小为 sz 的矩阵返回由 row 和 col 指定的行列下标的对应线性索引 ind。此处,sz 是包含两个元素的向量,其中 sz(1) 指定行数,sz(2) 指定列数。
ind2sub将线性索引转换为下标[row,col] = ind2sub(sz,ind) 返回数组 row 和 col,其中包含与大小为 sz 的矩阵的线性索引 ind 对应的等效行和列下标。此处,sz 是包含两个元素的向量,其中 sz(1) 指定行数,sz(2) 指定列数。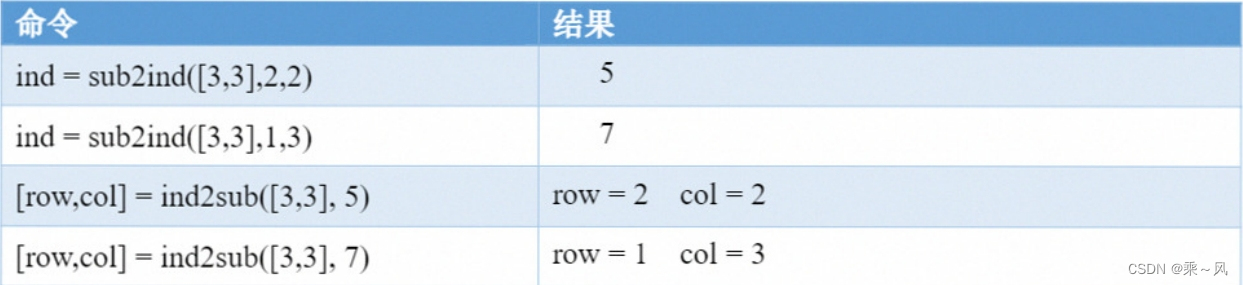
矩阵元素的修改和删除
1、可以直接利用等号赋值的方法对引用位置的元素进行修改,用法和对向量元素的修改类似。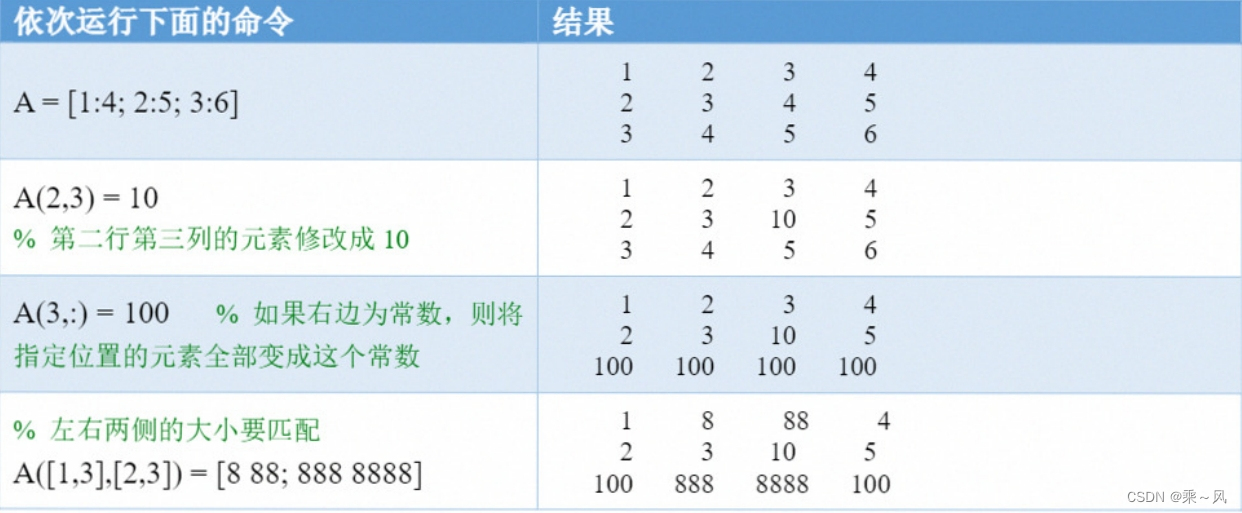
2、可以使用线性索引(单下标的索引)的方式对矩阵的元素进行修改: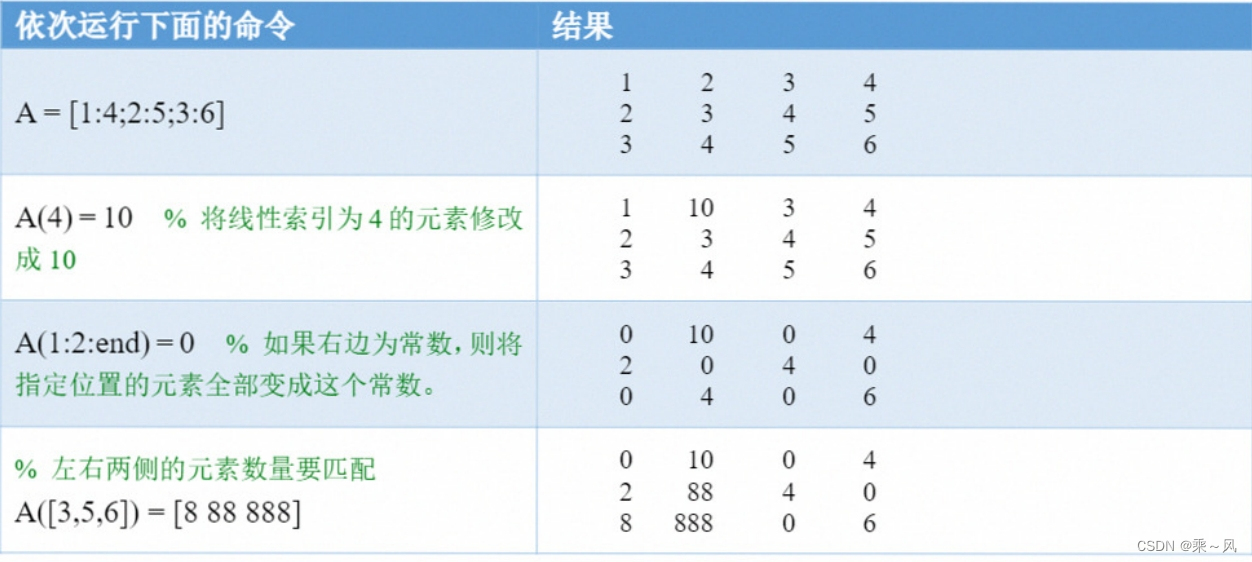
3、对矩阵进行拓展
通过将一个或多个元素置于矩阵现有的行和列索引边界之外,可以将它们添加到矩阵中。MATLAB 会自动用 0 填充矩阵,使其保持为矩形。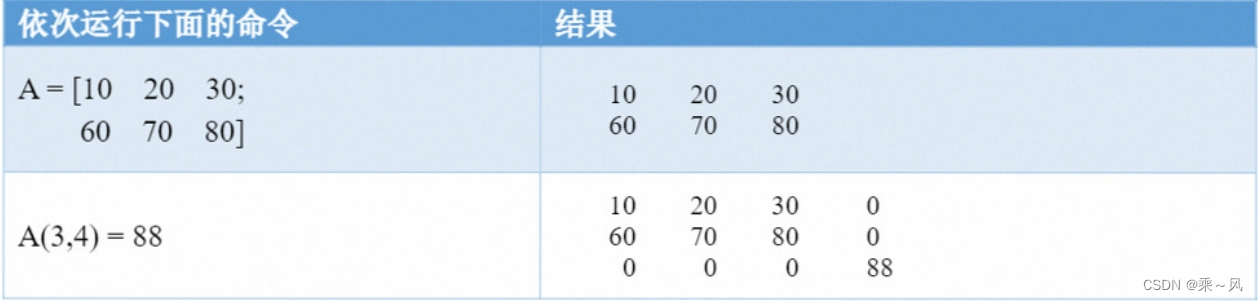
还可以通过在现有索引范围之外插入新矩阵来扩展其大小。
如果我们将等号右侧变成空向量[ ],则可以删除对应位置的元素。需要注意的是,通常只能删除矩阵的整行或者整列,否则会报错。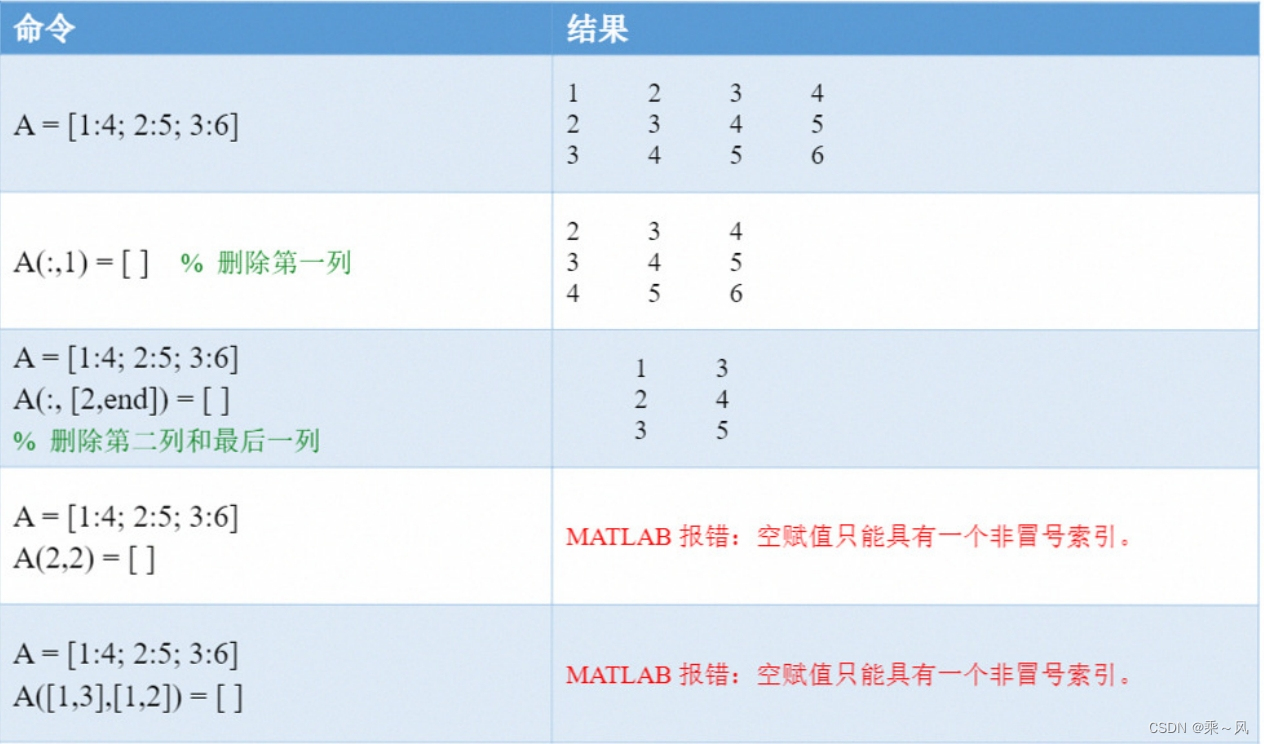
注意,也可以通过线性索引来删除矩阵的元素。使用线性索引删除后,MATLAB会将矩阵中剩下的元素按照线性索引的顺序放入到一个向量中。另外,使用线性索引可以删除任意位置的元素,不需要删除矩阵的一整行或者一整列。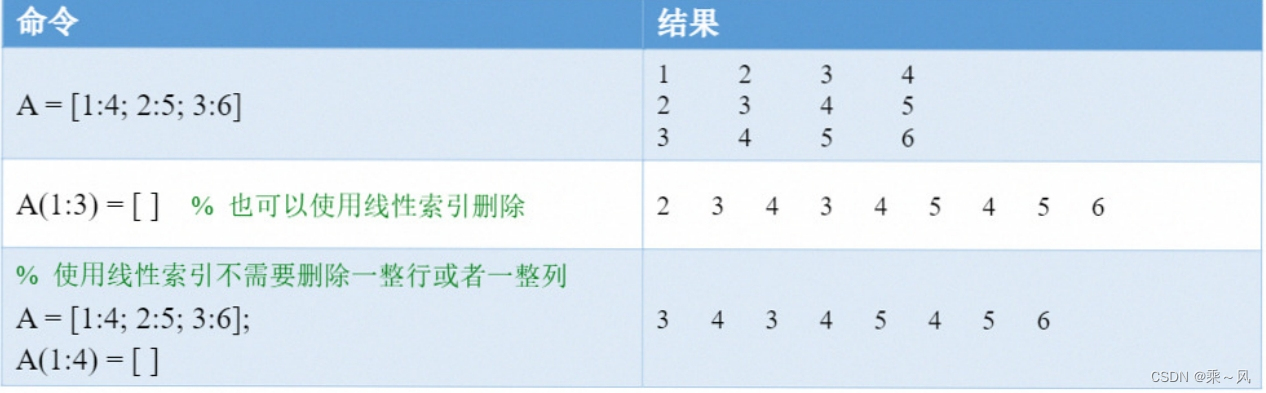
矩阵的拼接和重复
矩阵的拼接
有时候我们需要对多个矩阵进行拼接,变成一个大的矩阵。
根据矩阵拼接的方向,我们可以分为横向(水平)拼接和纵向(垂直)拼接,如下图所示:
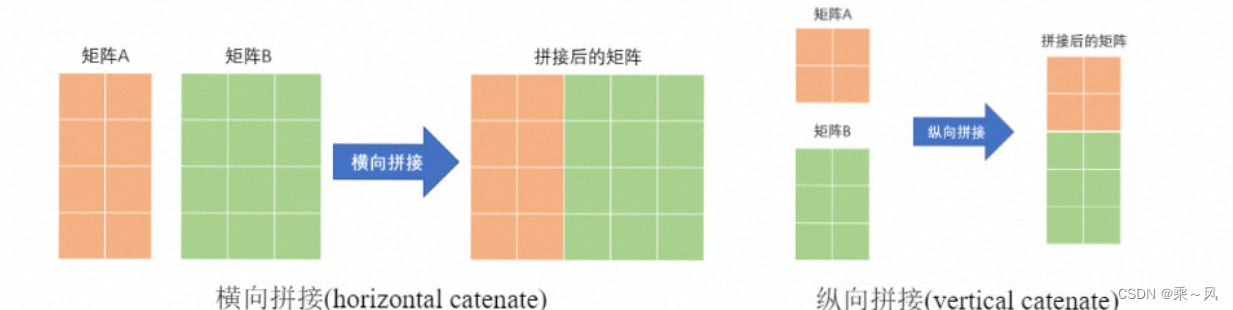
如上图所示:横向拼接要求矩阵的行数相同;纵向拼接要求矩阵的列数相同。
在MATLAB中,我们可以使用命令[A, B] 或 [A B]对矩阵A和B进行横向拼接,也可以使用MATLAB中的内置函数:horzcat(A,B);
A = [1 6 7; 4 5 7]
B = [3 1; 5 10]
[A, B]
[A B] % 用空格隔开,可以有多个空格
horzcat(A,B)
cat(2,A,B)
类似的,我们可以使用命令[A; B]对矩阵A和B进行纵向拼接,也可以使用MATLAB中的内置函数:vertcat(A,B)。
A = [2 4 5;2 2 4]
B = [1 8 6;6 3 10;1 5 5]
[A; B]
[A
B] % 也可以使用回车键进行纵向拼接
vertcat(A,B)
cat(1,A,B)
下面是cat函数的帮助链接:
https://ww2.mathworks.cn/help/matlab/ref/double.cat.html
命令cat(dim,A,B)表示沿维度 dim 方向将矩阵B拼接到矩阵A的末尾。
dim = 1时表示从上自下沿着行方向拼接,即纵向拼接,因此cat(1,A,B)等价于vertcat(A,B);
dim = 2时表示从左自右沿着列方向拼接,即横向拼接,因此cat(2,A,B)等价于horzcat(A,B)。
大小不匹配会报错
矩阵的重复
有时候我们需要对同一个矩阵进行重复的堆叠。
例如将矩阵A的内容堆叠在m行n列的新矩阵中,这个新矩阵每一行由n个A组成,每一列由m个A组成。
下面我们画一个示意图:
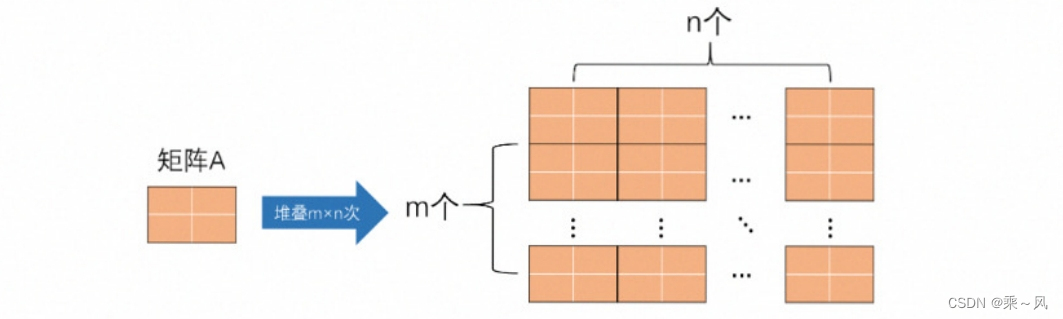
在MATLAB中,对同一个矩阵进行重复的堆叠的代码为repmat(A,m,n)。
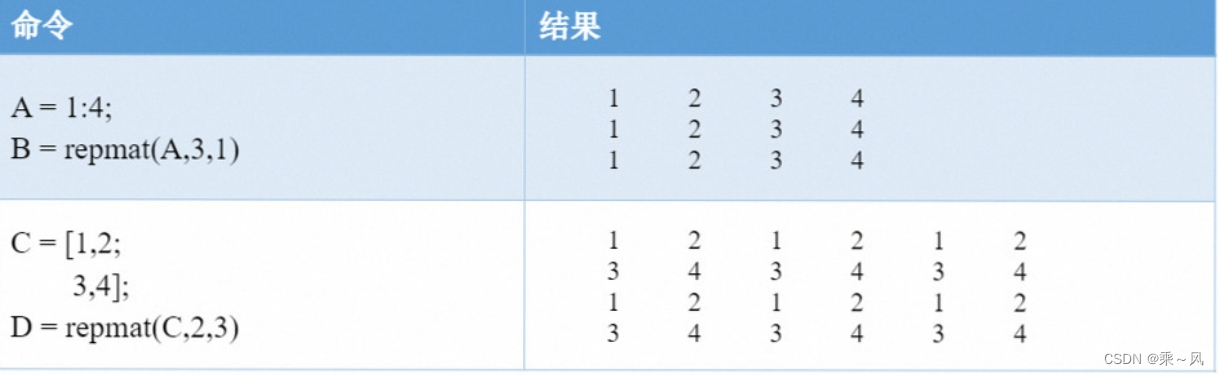
对向量或者矩阵中的元素进行重复,使用到的函数是repelem。(使用较少)
情况1:重复向量v中的元素:repelem(v,n)
当n为一个正整数时,表示把向量v中的每一个元素都重复n次;
n也可以为一个向量,其长度必须和v的长度相同,它可以将v的每个元素指定重复n对应元素的次数。
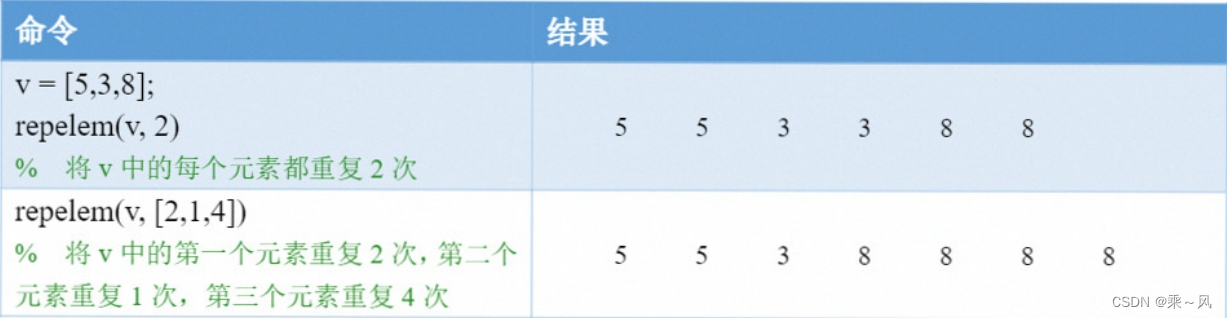
情况2:重复矩阵A中的元素:repelem(A,m,n)
m和n分别表示沿着行方向(从上至下)和列方向(从左至右)将矩阵元素重复的次数,这里的m和n可以是正整数,也可以是向量。
如果m是向量,则m的长度要和矩阵A的行数相同;如果n是向量,则n的长度要和矩阵A的列数相同。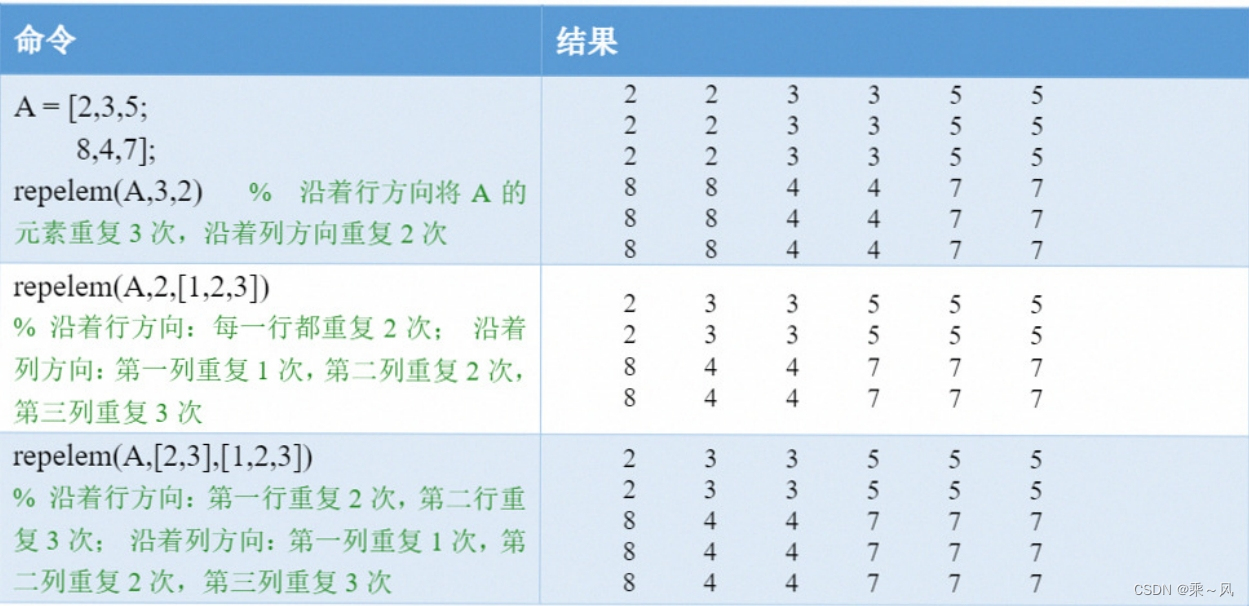
若有侵权,请联系作者
相关文章:

MATLAB矩阵的操作(第二部分)
师从清风 矩阵的创建方法 在MATLAB中,矩阵的创建方法主要有三种,分别是:直接输入法、函数创建法和导入本地文件中的数据。 直接输入法 输入矩阵时要以中括号“[ ]”作为标识符号,矩阵的所有元素必须都在中括号内。 矩阵的同行元…...
基础面试题整理6之Redis
1.Redis的应用场景 Redis支持类型:String、hash、set、zset、list String类型 hash类型 set类型 zset类型 list类型 一般用作缓存,例如 如何同时操作同一功能 2.redis是单线程 Redis服务端(数据操作)是单线程,所以Redis是并发安全的,因…...
-常用的字符串函数)
MySQL基础查询篇(7)-常用的字符串函数
MySQL数据库是目前广泛应用于各种系统中的一种关系型数据库管理系统。在MySQL中,有许多常见的字符串函数,可以对字符串进行各种处理和操作。本文将介绍MySQL数据库中常用的一些字符串函数,并提供详细示例。 CONCAT函数:用于将两个…...

如何实现视线(目光)的检测与实时跟踪
如何实现视线(目光)的检测与实时跟踪 核心步骤展示说明 找到人脸 检测人脸特征点 根据特征点找到人眼区域 高精度梯度算法检测瞳孔中心 根据眼睛周边特征点计算眼睛中心 瞳孔中心和眼睛中心基于视线模型计算视线方向 视线方向可视化 详细实现与说明: https://stud…...
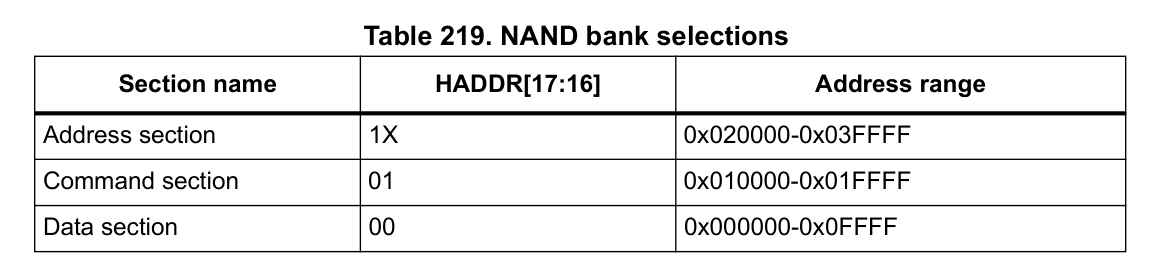
STM32 FSMC (Flexible static memory controller) 灵活静态内存控制器介绍
文章目录 1. 介绍FSMC2. FSMC特点3. Block示意图4. AHB接口4.1 Supported memories and transactionsGeneral transaction rulesConfiguration registers 5. 外部设备地址映射5.1 NOR/PSRAM地址映射将NOR Flash/PSRAM的支持进行封装 5.2 NAND/PC Card地址映射 1. 介绍FSMC 说到…...

手把手教你开发Python桌面应用-PyQt6图书管理系统-图书信息维护模块UI设计实现
锋哥原创的PyQt6图书管理系统视频教程: PyQt6图书管理系统视频教程 Python桌面开发 Python入门级项目实战 (无废话版) 火爆连载更新中~_哔哩哔哩_bilibiliPyQt6图书管理系统视频教程 Python桌面开发 Python入门级项目实战 (无废话版) 火爆连载更新中~共计24条视频&…...
WebMvc场景的自动装配)
SpringBoot源码解读与原理分析(六)WebMvc场景的自动装配
文章目录 2.6 WebMvc场景下的自动装配原理2.6.1 WebMvcAutoConfiguration2.6.2 Servlet容器的装配2.6.2.1 EmbeddedTomcat、EmbeddedJetty、EmbeddedUndertow2.6.2.2 BeanPostProcessorsRegistrar(后置处理器的注册器)2.6.2.3 两个定制器的注册 2.6.3 DispatcherServlet的装配2…...

git恢复rebase过程中遇到权限问题和丢失的提交
文章目录 一、检查丢失的提交是否还在 reflog 中二、创建一个新分支来恢复丢失的提交三、处理权限问题四. 使用 git fsck 查找丢失对象1、创建一个新分支来恢复该提交2、检查和合并提交 五. 介绍git中命令reflog 与 fsck1、git reflog2、git fsck使用场景 一、检查丢失的提交是…...

Spring boot 集成redis
一、使用spring bootspring-boot-starter-data-redis 导入maven包 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifactId> </dependency> spring boot配置文件 spring.re…...
概述)
c++ STL系列——(一)概述
引言 在软件开发的世界里,C一直是一门备受青睐的编程语言,特别是在需要高性能和灵活性的场合。而C的标准模板库(Standard Template Library,简称STL)无疑是这门语言中最强大的工具之一。STL提供了一系列的数据结构和算…...

AI-数学-高中-25-三角函数一图像解决三角函数不等式
原作者视频:【三角函数】【考点精华】1图像解决三角函数不等式问题(基础)_哔哩哔哩_bilibili 1.三角函数图像法; 2.不好画图像时:任意角的三角函数图像,在象限中比较,在4个象限中寻找角度的关系。 示例1…...

在Ubuntu上安装JetBrains Toolbox并解决libfuse.so.2依赖问题
在安装JetBrains Toolbox的过程中,我们遇到了libfuse.so.2依赖缺失的问题。这个问题通常发生在尝试运行AppImage格式的程序时,如果系统缺少必要的FUSE(Filesystem in Userspace)支持。以下是我在解决这个问题并在Ubuntu上成功安装…...
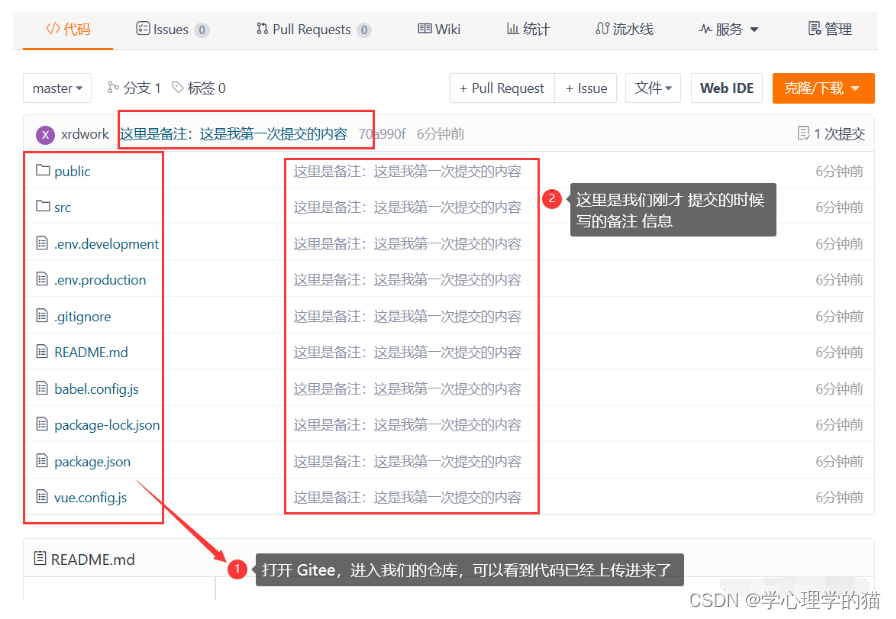
在vscode上传项目到gitee
一、在Gitee上新建一个仓库 Tip:若已经创建过了,直接跳到第二部分看VsCode如何上传代码到Gitee 创建仓库比较简单,下面两张图就是整个过程,这里不在赘述,具体如下: 二、VsCode连接Gitee上创建的仓…...

比较两次从接口获取的数据,并找出变动的字段
问题:有这么一个接口数据,每次会返回这么一个数据: [{Id:1,pending:65,queued:0,completed:0},{Id:2,pending:0,queued:0,completed:0}],请问再次请求这个接口的时候如何将获取的数据和上一次获取到的数据进行比较,找出变动的字段…...

Java并发基础:LinkedBlockingDeque全面解析!
内容概要 LinkedBlockingDeque提供了线程安全的双端队列实现,它支持在队列两端高效地进行插入和移除操作,同时具备阻塞功能,能够很好地协调生产者与消费者之间的速度差异,其内部基于链表结构,使得并发性能优异&#x…...
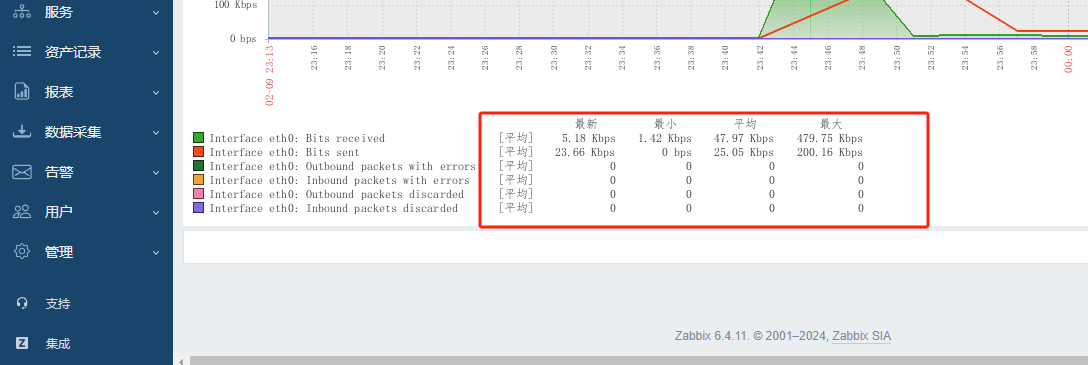
Zabbix6.x配置中文界面 解决乱码问题
Zabbix6.x配置中文界面 解决乱码问题 Zabbix6.x界面无法选择中文,通过安装语言包解决。后面也解决了zabbix6中文方块(乱码)问题。 配置中文语言包 系统中默认没有携带中文语言包,可以通过以下命令查看 localectl list-locales #…...
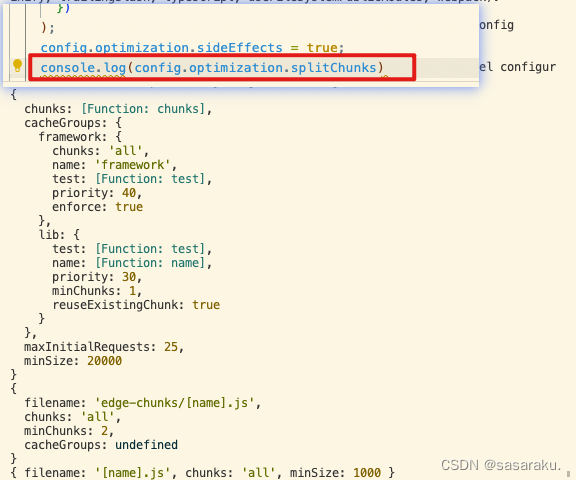
next项目页面性能调优
next项目页面性能调优 一般来说性能优化可以分为加载时、运行时两部分的优化。 扩展参考链接: 前端性能优化 24 条建议 Webpack 4进阶–从前的日色变得慢 ,一下午只够打一次包 Webpack 分包优化首屏加载 参考指标 FCP(First Contentful P…...

性能评测|虚拟化和裸金属 K8s 哪个性能更好?
本文重点 整体而言,SKS(虚拟机 Kubernetes)可以达到裸金属 Kubernetes 性能的 82% – 96%,满足绝大部分场景下生产容器应用的性能需求。更多虚拟化与裸金属 Kubernetes 架构、特性、适用场景与性能对比,欢迎阅读文末电…...

【大厂AI课学习笔记】【1.6 人工智能基础知识】(1)人工智能、机器学习、深度学习之间的关系
6.1 人工智能、机器学习与深度学习的关系 必须要掌握的内容: 如上图:人工智能>机器学习>深度学习。 机器学习是人工智能的一个分支,该领域的主要研究对象是人工智能,特别是如何在经验学习中改进具体算法的性能。 深度学习…...

计算机毕业设计基于的农村蔬菜销售系统SSM
项目运行 环境配置: Jdk1.8 Tomcat7.0 Mysql HBuilderX(Webstorm也行) Eclispe(IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持)。 项目技术: vue mybatis Maven mysql5.7或8.0等等组成,B…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...
