探索设计模式:原型模式深入解析
探索设计模式:原型模式深入解析
设计模式是软件开发中用于解决常见问题的标准解决方案。它们不仅能提高代码的可维护性和可复用性,还能让其他开发者更容易理解你的设计决策。今天,我们将聚焦于创建型模式之一的原型模式(Prototype Pattern),并通过具体的代码示例来深入了解它。
原型模式简介
原型模式是用于创建对象的设计模式,其思想是通过复制一个已存在的实例来创建新的实例,而不是通过新建类的方式。这种模式特别适用于创建复杂对象的情况,特别是当对象的创建过程比复制现有实例更加昂贵或复杂时。
应用场景
- 当直接创建一个对象的成本较高时,例如,需要进行复杂的数据库操作或网络请求。
- 当需要一个与现有对象相同或相似的对象时,但又希望两者相互独立。
原型模式的核心组件
原型模式主要涉及两个核心组件:
- 原型(Prototype):定义用于复制现有对象以产生新对象的接口。
- 具体原型(Concrete Prototype):实现原型接口的类,定义复制自身的操作。
原型模式的代码示例
为了更好地理解原型模式,让我们通过一个简单的例子:克隆一个图形对象。
定义原型接口
首先,我们定义一个原型接口,它包含了一个用于克隆对象的方法。
public interface Prototype {Prototype clone();
}
实现具体原型
接下来,我们创建一个具体的原型类,实现上述接口。
public class Rectangle implements Prototype {private int width;private int height;// 构造函数public Rectangle(int width, int height) {this.width = width;this.height = height;}// 拷贝构造函数,用于克隆public Rectangle(Rectangle target) {if (target != null) {this.width = target.width;this.height = target.height;}}@Overridepublic Prototype clone() {return new Rectangle(this);}// Getters and Setterspublic int getWidth() {return width;}public void setWidth(int width) {this.width = width;}public int getHeight() {return height;}public void setHeight(int height) {this.height = height;}
}
使用原型模式
现在我们可以使用原型模式来克隆对象了。
public class PrototypeDemo {public static void main(String[] args) {Rectangle rect1 = new Rectangle(10, 20);Rectangle rect2 = (Rectangle) rect1.clone();System.out.println("Rectangle 1 width: " + rect1.getWidth() + " height: " + rect1.getHeight());System.out.println("Rectangle 2 width: " + rect2.getWidth() + " height: " + rect2.getHeight());}
}
在这个示例中,我们创建了一个Rectangle对象rect1,并使用clone方法创建了一个新的Rectangle对象rect2。由于clone方法创建了rect1的一个深拷贝,因此rect2和rect1虽然内容相同,但是是完全独立的两个实例。
总结
原型模式提供了一种简便的方式来创建对象,特别是对于创建成本高昂或需要独立于其类和如何创建的对象的情况。通过实现一个克隆自身的方法,可以在不知道对象类型的情况下生成新的实例,这增加了代码的灵活性和可复用性。希
望通过这篇文章,你能对原型模式有一个更深入的了解,并在合适的场景中应用它。
相关文章:

探索设计模式:原型模式深入解析
探索设计模式:原型模式深入解析 设计模式是软件开发中用于解决常见问题的标准解决方案。它们不仅能提高代码的可维护性和可复用性,还能让其他开发者更容易理解你的设计决策。今天,我们将聚焦于创建型模式之一的原型模式(Prototyp…...

IAR报错解决:Fatal Error[Pe1696]: cannot open source file “zcl_ha.h“
报错信息 Fatal Error[Pe1696]: cannot open source file "zcl_ha.h" K:\Z-Stack 3.0.2\Projects\zstack\Practice\SampleSwitch\Source\zcl_samplesw_data.c 51 意思是找不到zcl_ha.h文件 找不到的理由可能是我把例程复制了一份到别的文件目录下,少复制…...
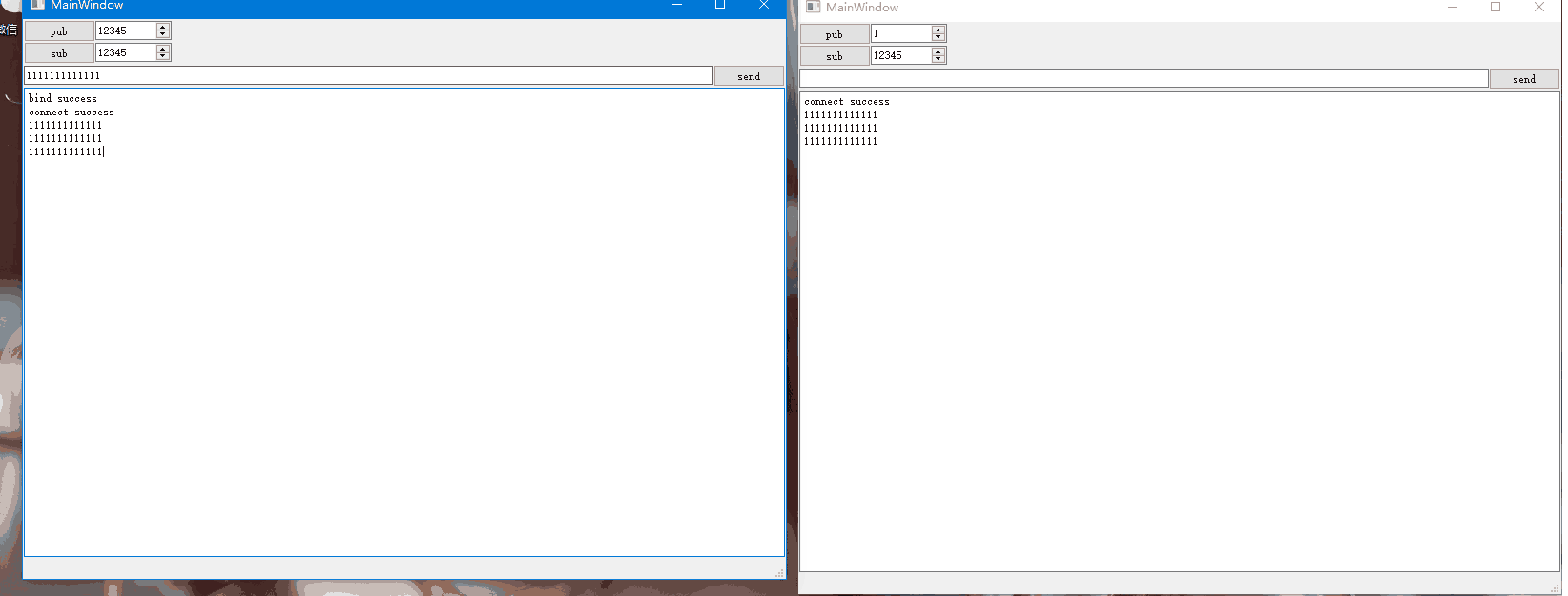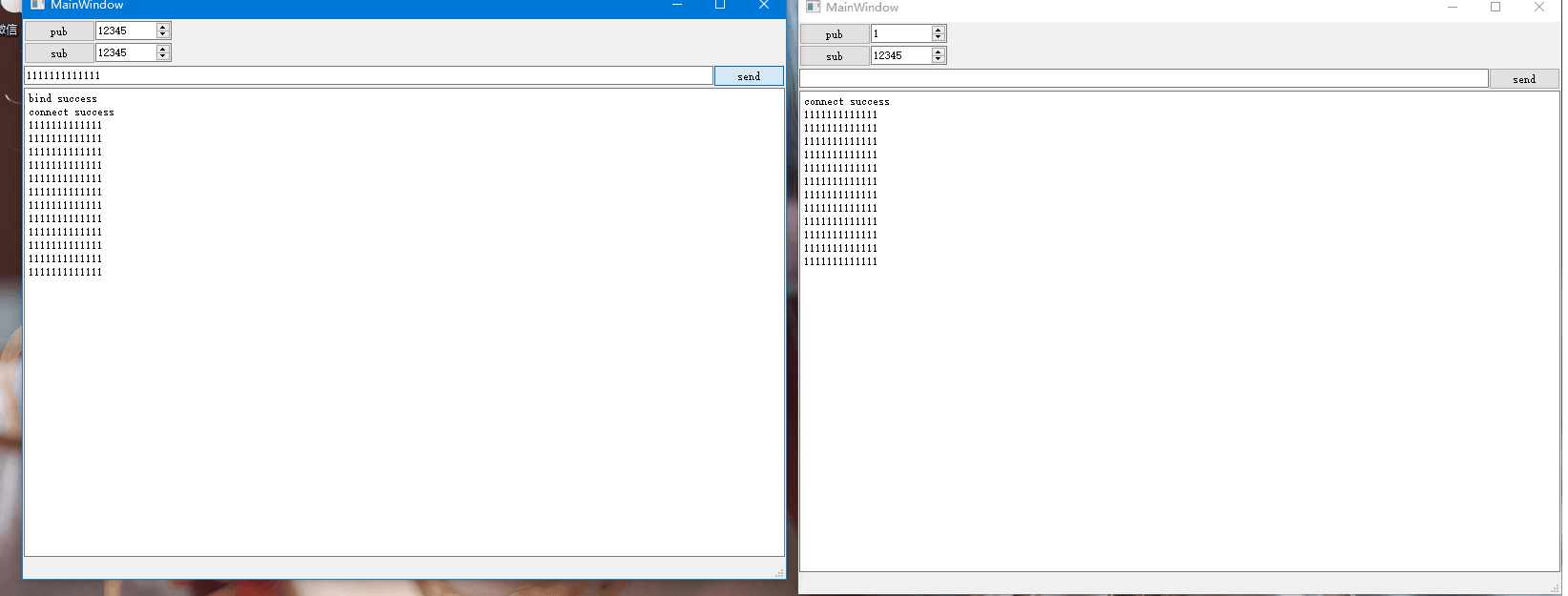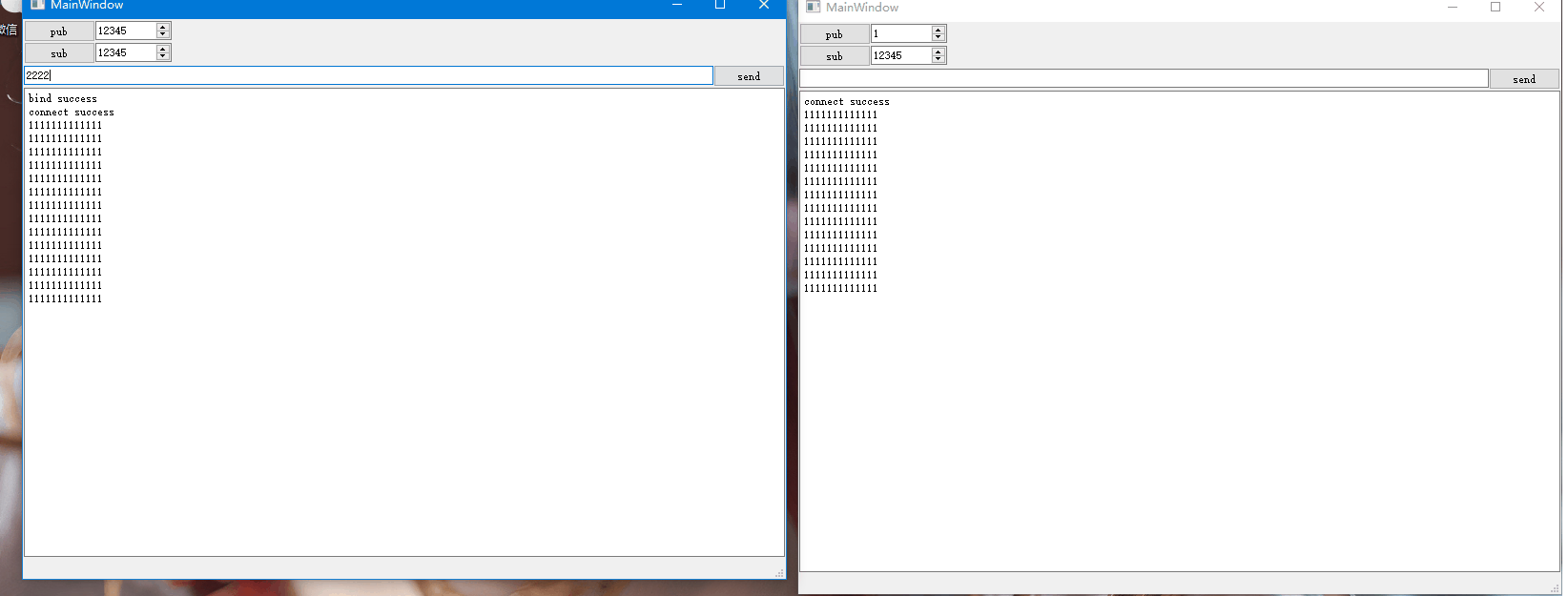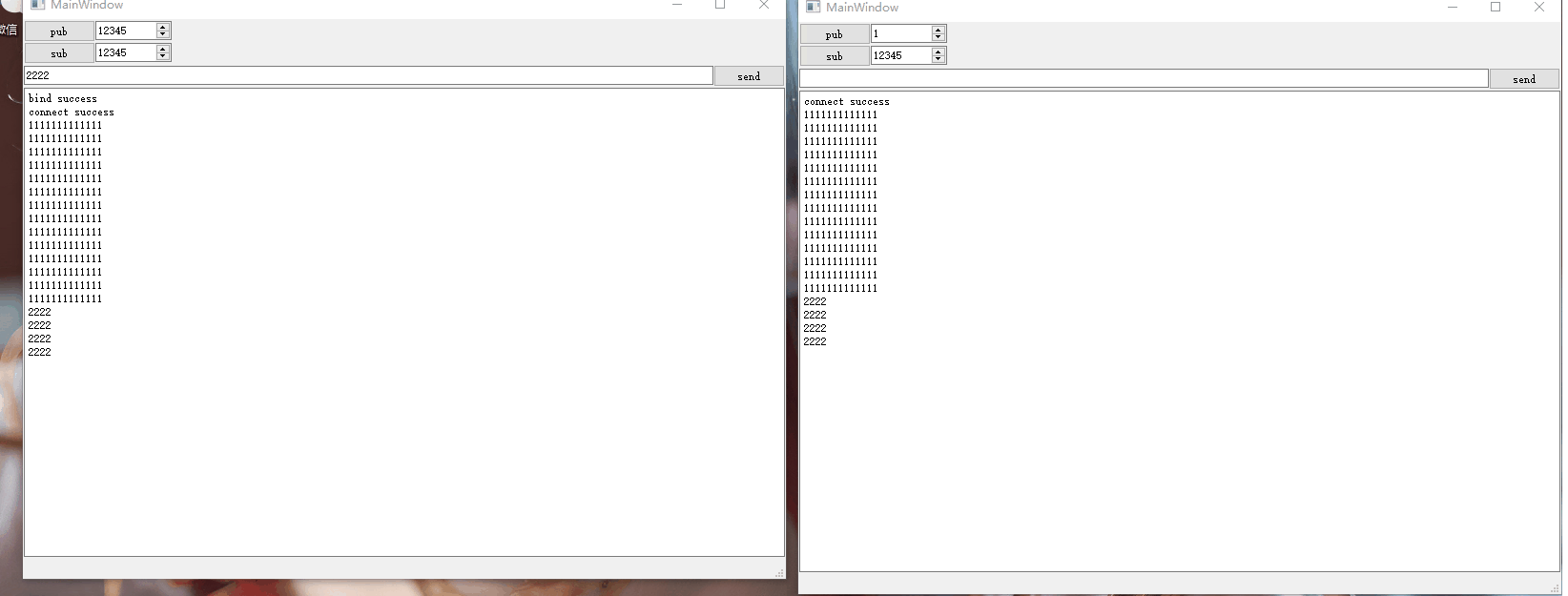
Qt网络编程-ZMQ的使用
不同主机或者相同主机中不同进程之间可以借助网络通信相互进行数据交互,网络通信实现了进程之间的通信。比如两个进程之间需要借助UDP进行单播通信,则双方需要知道对方的IP和端口,假设两者不在同一主机中,如下示意图: …...

如何清理Docker占用的磁盘空间?
在Docker中,随着时间的推移,占用的磁盘空间可能会不断增加。为了保持系统的稳定性和性能,定期清理Docker占用的磁盘空间非常重要。下面将介绍一些清理Docker磁盘空间的方法。 一、清理无用的容器 有时候,我们可能会运行一些临时…...

从零开始学HCIA之NAT基本工作原理
1、NAT设计之初的目的是解决IP地址不足的问题,慢慢地其作用发展到隐藏内部地址、实现服务器负载均衡、完成端口地址转换等功能。 2、NAT完成将IP报文报头中的IP地址转换为另一个IP地址的过程,主要用于实现内部网络访问外部网络的功能。 3、NAT功能一般…...

Day40- 动态规划part08
一、单词拆分 题目一:139. 单词拆分 139. 单词拆分 给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。 注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以…...

论文笔记:相似感知的多模态假新闻检测
整理了RecSys2020 Progressive Layered Extraction : A Novel Multi-Task Learning Model for Personalized Recommendations)论文的阅读笔记 背景模型实验 论文地址:SAFE 背景 在此之前,对利用新闻文章中文本信息和视觉信息之间的关系(相似…...

5G技术对物联网的影响
随着数字化转型的加速,5G技术作为通信领域的一次重大革新,正在对物联网(IoT)产生深远的影响。对于刚入行的朋友们来说,理解5G技术及其对物联网应用的意义,是把握行业发展趋势的关键。 让我们简单了解什么是…...
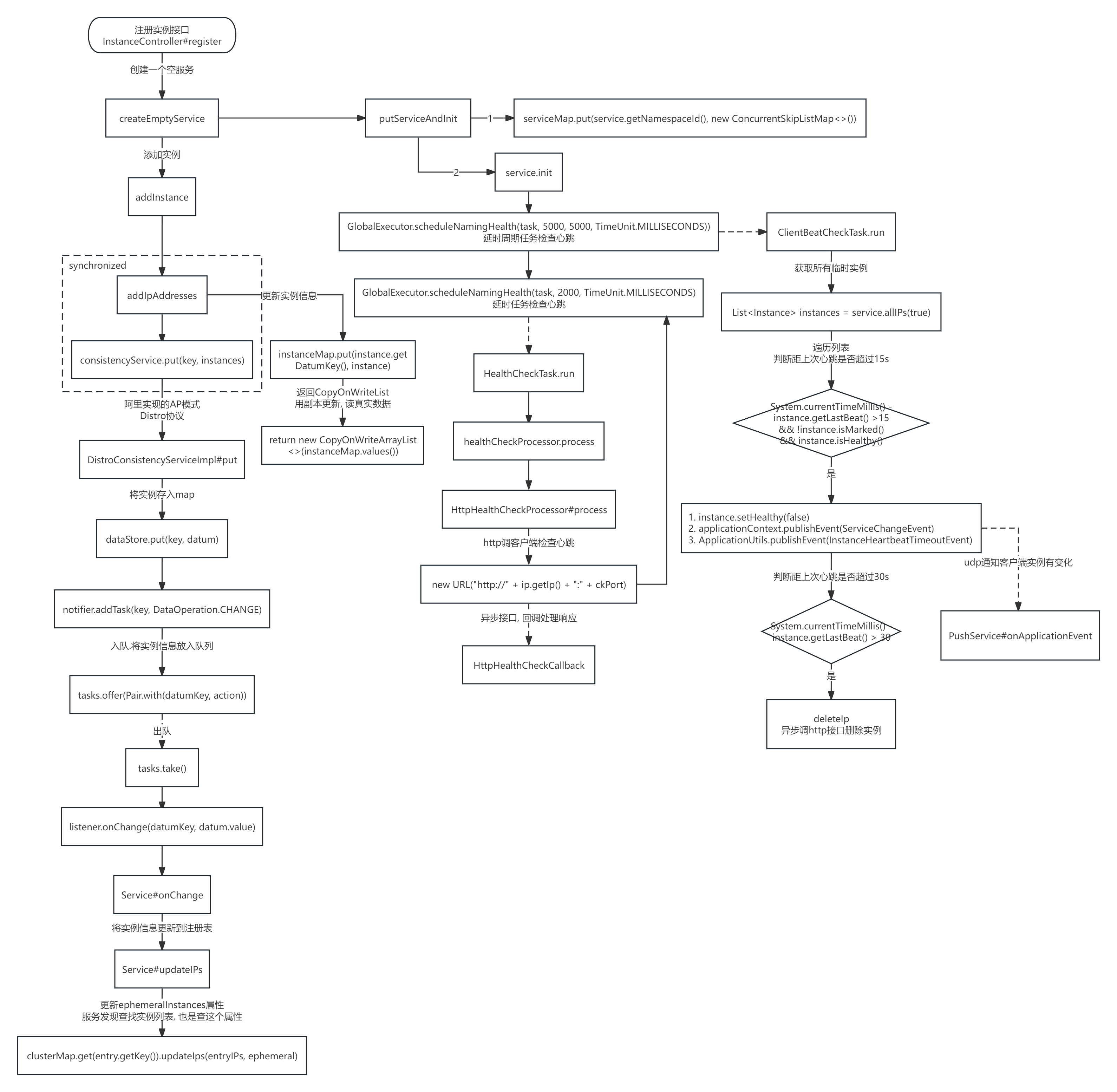
Nacos1.X源码解读(待完善)
目录 下载源码 注册服务 客户端注册流程 注册接口API 服务端处理注册请求 设计亮点 服务端流程图 下载源码 1. 克隆git地址到本地 # 下载nacos源码 git clone https://github.com/alibaba/nacos.git 2. 切换分支到1.4.7, maven编译(3.5.1) 3. 找到启动类com.alibaba.na…...

算法之双指针系列1
目录 一:双指针的介绍 1:快慢指针 2:对撞指针 二:对撞指针例题讲述 一:双指针的介绍 在做题中常用两种指针,分别为对撞指针与快慢指针。 1:快慢指针 简称为龟兔赛跑算法,它的基…...

苍穹外卖面试题
8. 如何理解分组校验 很多情况下,我们会将校验规则写到实体类中的属性上,而这个实体类有可能作为不同功能方法的参数使用,而不同的功能对象参数对象中属性的要求是不一样的。比如我们在新增和修改一个用户对象时,都会接收User对象…...
【Qt 学习之路】在 Qt 使用 ZeroMQ
文章目录 1、概述2、ZeroMQ介绍2.1、ZeroMQ 是什么2.2、ZeroMQ 主线程与I/O线程2.3、ZeroMQ 4种模型2.4、ZeroMQ 相关地址 3、Qt 使用 ZeroMQ3.1、下载 ZeroMQ3.2、添加 ZeroMQ 库3.3、使用 ZeroMQ3.4、相关 ZeroMQ 案例 1、概述 今天是大年初一,先给大家拜个年&am…...

CI/CD到底是啥?持续集成/持续部署概念解释
前言 大家好,我是chowley,日常工作中,我每天都在接触CI/CD,今天就给出我心中的答案。 在现代软件开发中,持续集成(Continuous Integration,CI)和持续部署(Continuous D…...
)
golang常用库之-disintegration/imaging图片操作(生成缩略图)
文章目录 golang常用库之什么是imaging库导入和使用生成缩略图 golang常用库之 什么是imaging库 官网:https://github.com/disintegration/imaging imaging 是一个 Go 语言的图像处理库,它提供了一组功能丰富的函数和方法,用于进行各种图像…...

CSS 控制 video 标签的控制栏组件的显隐
隐藏下载功能 <video src"" controlsList"nodownload" />controlslist 取值如下(设定多个值则使用空格进行间隔) 如:controlslist"nodownload nofullscreen noremoteplayback"nodownload:取消更多控件弹窗的下载功…...

数据可视化之维恩图 Venn diagram
文章目录 一、前言二、主要内容三、总结 🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一、前言 维恩图(Venn diagram),也叫文氏图或韦恩图,是一种关系型图表,用于显示元素集合之间的重叠区…...

2024刘谦春晚第二个扑克牌魔术
前言 就是刚才看春晚感觉这个很神奇,虽然第一个咱模仿不过来,第二个全国人民这么多人,包括全场观众都有成功,这肯定是不需要什么技术,那我觉得这个肯定就是数学了,于是我就胡乱分析一通。 正文 首先准备…...
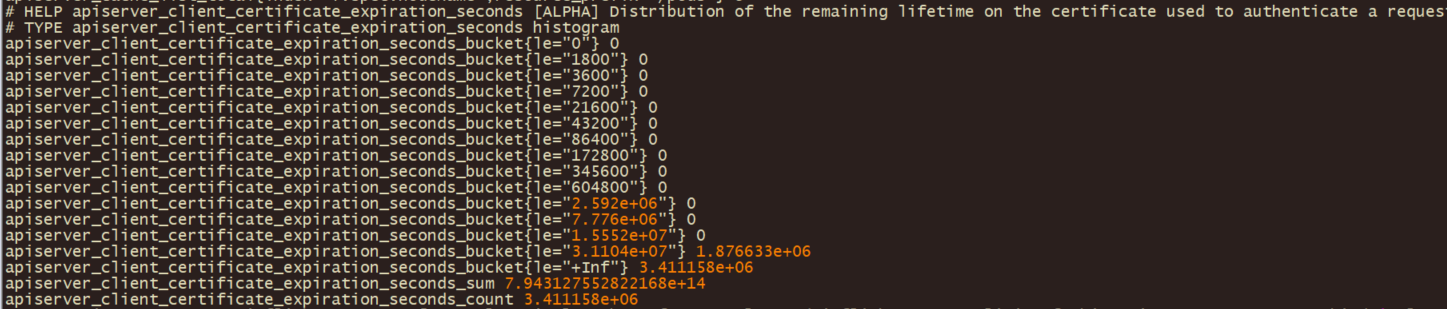
【k8s系列】(202402) 证书apiserver_client_certificate_expiration_seconds
apiserver_client_certificate_expiration_second证书定义的位置:kubernetes/staging/src/k8s.io/apiserver/pkg/authentication/request/x509/x509.go at 244fbf94fd736e94071a77a8b7c91d81163249d4 kubernetes/kubernetes (github.com) apiserver_client_certi…...

Rust变量与常量介绍
Rust是一门注重安全性和性能的系统编程语言,其中变量和常量的概念有着独特的设计和特性。在本文中,我们将深入了解Rust中的变量和常量,并解释它们之间的区别,同时通过多个例子进行说明。 Rust常量 在Rust中,常量是不…...

Flask基础学习2
连接mysql数据库测试(专业版) [注意1:要导入text库,否则可能出现找不到select 1错误] [注意2:若出现下列问题,可按照模板代码的顺序db SQLAlchemy(app) 的位置] RuntimeError: Either SQLALCHEMY_DATABASE_URI or SQLALCHEMY_B…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...
