【数据结构】13:表达式转换(中缀表达式转成后缀表达式)
思想:
从头到尾依次读取中缀表达式里的每个对象,对不同对象按照不同的情况处理。
- 如果遇到空格,跳过
- 如果遇到运算数字,直接输出
- 如果遇到左括号,压栈
- 如果遇到右括号,表示括号里的中缀表达式已经扫描完毕,将栈顶的运算符弹出并输出, 直至遇到左括号(左括号出栈但是不输出)
- 若遇到运算符,若当前运算符优先级高于栈顶运算符,将其压栈; 若小于等于栈顶元素的优先级,将栈顶运算符弹出并输出,再比较新的栈顶运算符,直到该运算符优先级高于栈顶运算符优先级为止,然后将其压栈。
- 若中缀表达式各个对象处理完毕,则把堆栈里的运算符一并输出。
示例
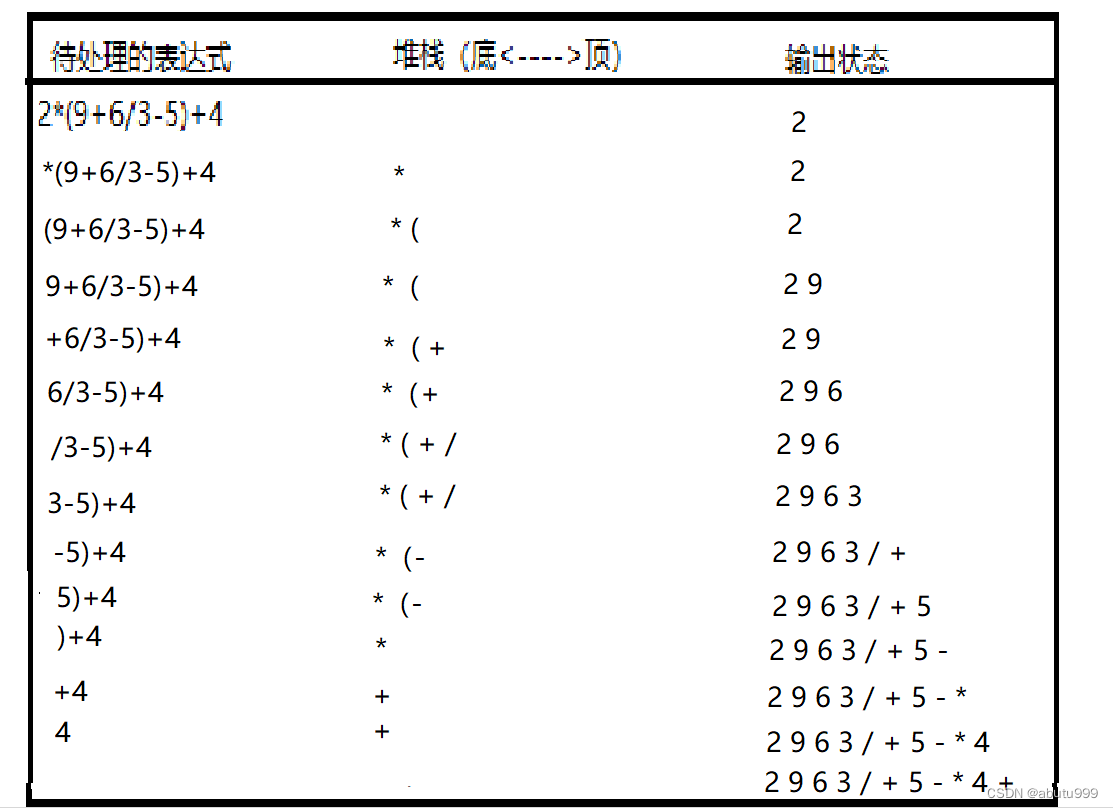
代码
int precedence(char op) {if (op == '+' || op == '-') return 1;else if (op == '*' || op == '/') return 2;else return 0; // 其他情况,比如括号等
}char* ExchangeToPost(char* Expr) {Stack S;S = CreateStack(100);int length = strlen(Expr);char* result = (char*)malloc(sizeof(char) * (length + 1));int i = 0;int j = 0;int k = 0;while (Expr[i] != '\0') {if (Expr[i] == ' ') {i++;}else if (isdigit(Expr[i])) {result[j] = Expr[i];//printf("case digital: result[%d]: %c\n", j, result[j]);j++;i++;}else if (Expr[i] == '(') {Push(S, Expr[i]);i++;}else if (Expr[i] == ')') {//print_s(S);char temp = Pop(S);while (temp != '(') {result[j] = temp;//printf("case ')': result[%d]: %c\n", j, result[j]);j++;temp = Pop(S);}i++;}else {if (IsEmpty(S)) {Push(S, Expr[i]);i++;continue;}char temp = Pop(S);if (temp == '(') {Push(S, temp);Push(S, Expr[i]);i++;continue;}if (precedence(Expr[i]) > precedence(temp)) {//printf("case opr: result[%d]: %c\n", j, result[j]);Push(S, temp);Push(S, Expr[i]);i++;}else {while (precedence(Expr[i]) <= precedence(temp)){result[j] = temp;//printf("case opr: result[%d]: %c\n", j, result[j]);j++;temp = Pop(S);}Push(S, temp);Push(S, Expr[i]);i++;}}//printf("i: %d, j: %d\n", i, j);//print_s(S);}while (!IsEmpty(S)) {result[j] = Pop(S);j++;}result[j] = '\0';return result;
}
相关文章:

【数据结构】13:表达式转换(中缀表达式转成后缀表达式)
思想: 从头到尾依次读取中缀表达式里的每个对象,对不同对象按照不同的情况处理。 如果遇到空格,跳过如果遇到运算数字,直接输出如果遇到左括号,压栈如果遇到右括号,表示括号里的中缀表达式已经扫描完毕&a…...
-视图的创建和应用)
MySQL进阶查询篇(9)-视图的创建和应用
数据库视图是MySQL中一个非常重要的概念。它是一个虚拟表,由一个查询的结果集组成。数据库视图为用户提供了一种简化数据查询和操作的方式。本文将介绍MySQL数据库视图的创建和应用。 1. 创建数据库视图 要创建MySQL数据库视图,我们使用CREATE VIEW语句…...
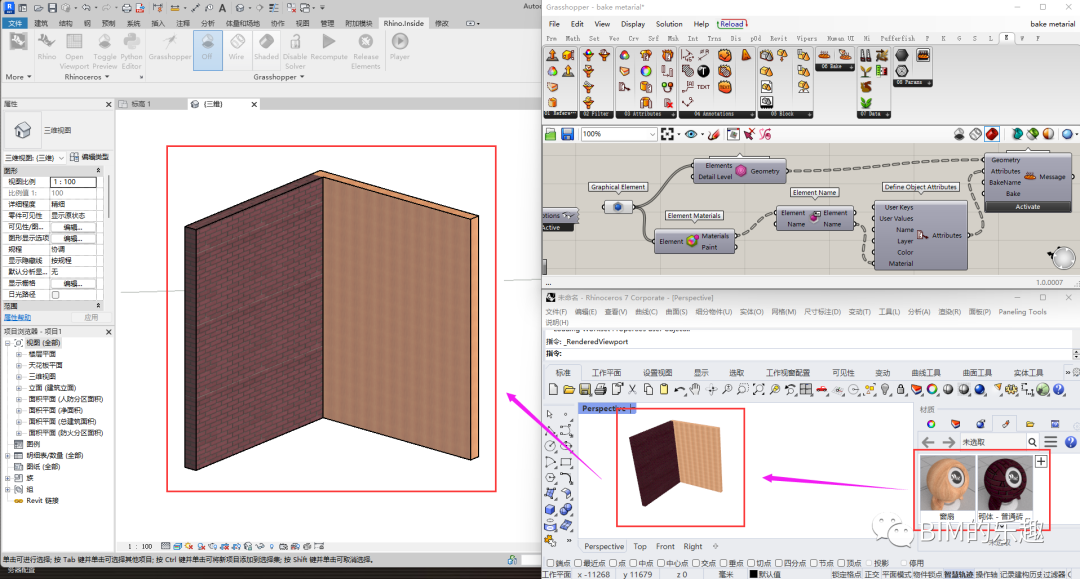
Rhino.Inside带材质将Revit模型bake到Rhino
Hello大家好!我是九哥~ 今天来讲一个小技巧,就是我通常采用RIR将Revit的模型的Geometry Bake到Rhino,肯定是没有材质的,那么如果我们需要带材质那要怎么办呢? 对于会的人,其实挺简单的,只需要…...

随记-Java项目处理SQL注入问题
现象:http://10.xx.xx.xx:xx/services/xxService 存在SQL注入情况 加固意见: 需要对网站所有参数中提交的数据进行过滤,禁止输入“"、"xor"、"or"、”--“、”#“、”select“、”and“等特殊字符;所有…...

精读《js 模块化发展》
1 引言 如今,Javascript 模块化规范非常方便、自然,但这个新规范仅执行了 2 年,就在 4 年前,js 的模块化还停留在运行时支持,10 年前,通过后端模版定义、注释定义模块依赖。对经历过来的人来说,…...
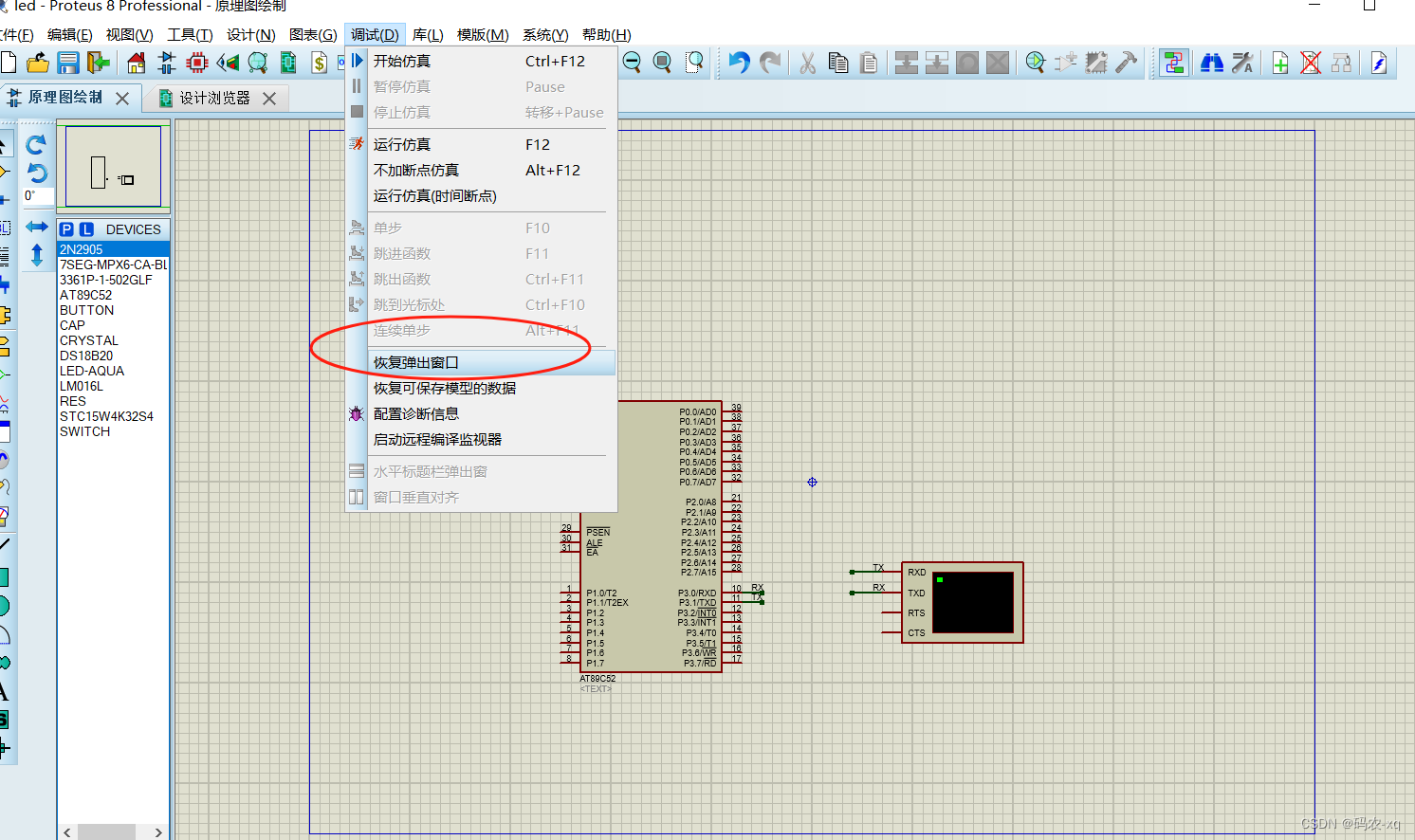
Proteus -模拟串口被关闭后怎样打开
Proteus -模拟串口被关闭后怎样打开 点击恢复弹出窗口,即可重新打开...

【深度学习】pytorch 与 PyG 安装(pip安装)
【深度学习】pytorch 与 PyG 安装(pip安装) 一、PyTorch安装和配置(一)、安装 CUDA(二)、安装torch、torchvision、torchaudio三个组件(1)下载镜像文件(2)创建…...

Bert与ChatGPT
1. Bert模型 BERT(Bidirectional Encoder Representations from Transformers)是一种预训练语言表示的方法,由Google AI在2018年提出。它标志着自然语言处理(NLP)领域的一个重大进步,因为它能够理解单词在…...
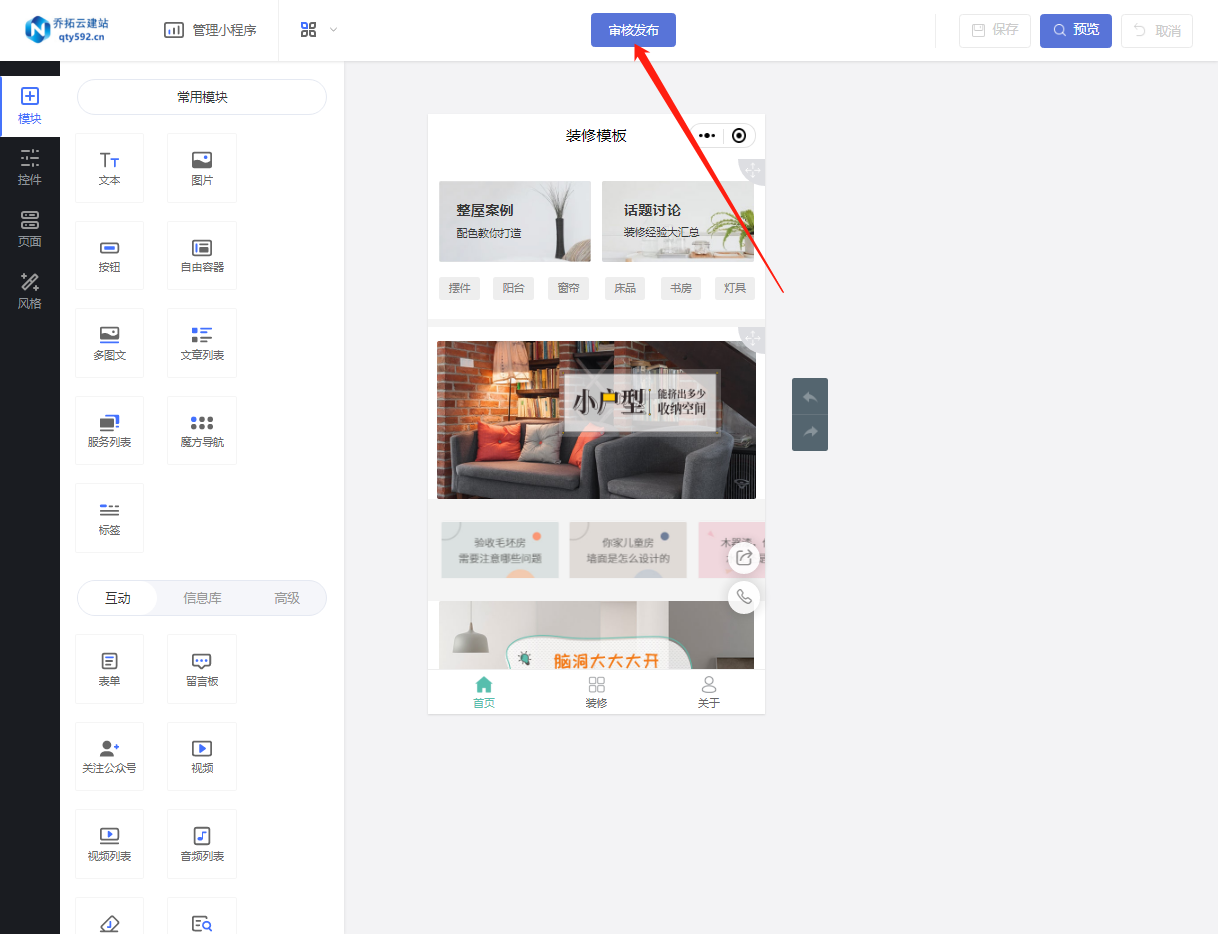
微信自动预约小程序开发指南:从小白到专家
随着互联网的发展,小程序已经成为了一个备受欢迎的在线预约平台。本文将详细介绍如何使用第三方制作平台,如乔拓云网,来搭建一个从入门到精通的预约小程序。 首先,我们需要登录乔拓云网,并选择一个适合自己的小程序模板…...
)
巴尔加瓦算法图解【完结】:算法运用(下)
目录 布隆过滤器HyperLogLogSHA算法比较文件检查密码 Diffie-Hellman密钥交换线性规划结语(完结) 布隆过滤器 在元素很多的情况下,判断一个元素是否在集合中可以使用布隆过滤器。布隆过滤器(Bloom Filter)是 1970 年由…...
hexo部署到gitee(码云)
引言 Hexo 是一个基于Node.js的静态博客框架,而 Gitee(也被称为码云)是一个国内的代码托管平台,支持 Git 版本控制系统,与 GitHub 类似。将 Hexo 部署到 Gitee Pages 可以让你的博客受益于 Gitee 的国内服务器…...

linux系统非关系型数据库memcached
memcached 特点原理配置安装Memcached 特点 内置内存存储方式-----------为了提高性能,memcached中保存的数据都存储在memcache内置的内存存储空间中。由于数据仅存在于内存中,重启操作系统会导致全部数据消失简单key/value存储---------------服务器不…...

前端vite+vue3——自动化配置路由布局
文章目录 ⭐前言💖vue3系列文章 ⭐ 自动化配置路由💖引入vite版本自定义目录映射💖自动化读取文件下的路由💖main入口加载路由💖入口app.vue配置💖layout基础布局配置💖效果 ⭐总结⭐结束 ⭐前言…...

速盾:怎么拿高防服务器做CDN
想要拿高防服务器做CDN,首先需要了解什么是CDN。CDN,即内容分发网络(Content Delivery Network),是一种通过互联网连接多个服务器,将静态和动态内容分发到最接近用户的服务器节点,从而提高用户访…...
SQLite database实现加密
注意:以下操作以VS2022为开发工具,以C#为开发语言。 数据加密原因 软件在使用的各个场景,很多都需要数据具有保密性,于是对于数据库就需要加密。特别是在某些特定领域或存储敏感数据尤其如此。 SQLite加密实现 SQLite加密有两种…...

Python requests模块 快速入门 这篇就够了
目录 一、Requests概述 二、安装Requests 三、Get请求 3.1 Get请求示例 3.2 Get请求爬取二进制数据 四、Post请求 4.1 Post请求示例 4.2 发送JSON数据 五、验证Cookies 六、会话请求 一、Requests概述 Requests是一个流行的Python第三方库,它专为HTTP通信…...

【VTKExamples::PolyData】第二十三期 InterpolateMeshOnGrid
很高兴在雪易的CSDN遇见你 VTK技术爱好者 QQ:870202403 前言 本文分享VTK样例InterpolateMeshOnGrid,并解析接口vtkProbeFilter 、vtkWarpScalar & vtkDealuany2D等多个接口,希望对各位小伙伴有所帮助! 感谢各位小伙伴的点赞+关注,小易会继续努力分享,一起进步!…...

大数据术语系列(1)——COW和MOR,我如何使用chatgpt通俗易懂地理解了hudi这两种表类型
从传统数据库到大数据的转变,首当其冲的是各种术语的理解。 所以我与chatgpt发生了一系列对话,以便于我能快速理解这些术语。 我先把汇总的结果放在前边,后边会一步步地来说明我是如何获取这些信息的。前边我也发过一些关于chatgpt提示词相…...

蓝桥杯基础知识7 vector
蓝桥杯基础知识7 vector vector 的定义和特性:在C中,vector是一个动态数组容器,可以存储一系列相同类型的元素。 vector 是一个模板类,使用之前包含头文件<vector>,声明一个vector对象vec,T是存储在v…...

【Java万花筒】加速Java应用程序:探索性能优化的利器
Java性能优化:提升应用程序效率与可靠性的关键 前言 在当今软件开发领域中,性能是一个至关重要的方面。对于Java应用程序而言,优化其性能可以带来更高的效率和更好的用户体验。本文将介绍一些常用的Java性能优化库和工具,帮助开…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...
