【机器学习】单变量线性回归
文章目录
- 线性回归模型(linear regression model)
- 损失/代价函数(cost function)——均方误差(mean squared error)
- 梯度下降算法(gradient descent algorithm)
- 参数(parameter)和超参数(hyperparameter)
- 代码实现样例
- 运行结果
源代码文件请点击此处!
线性回归模型(linear regression model)
- 线性回归模型:
f w , b ( x ) = w x + b f_{w,b}(x) = wx + b fw,b(x)=wx+b
其中, w w w 为权重(weight), b b b 为偏置(bias)
- 预测值(通常加一个帽子符号):
y ^ ( i ) = f w , b ( x ( i ) ) = w x ( i ) + b \hat{y}^{(i)} = f_{w,b}(x^{(i)}) = wx^{(i)} + b y^(i)=fw,b(x(i))=wx(i)+b
损失/代价函数(cost function)——均方误差(mean squared error)
- 一个训练样本: ( x ( i ) , y ( i ) ) (x^{(i)}, y^{(i)}) (x(i),y(i))
- 训练样本总数 = m m m
- 损失/代价函数是一个二次函数,在图像上是一个开口向上的抛物线的形状。
J ( w , b ) = 1 2 m ∑ i = 1 m [ f w , b ( x ( i ) ) − y ( i ) ] 2 = 1 2 m ∑ i = 1 m [ w x ( i ) + b − y ( i ) ] 2 \begin{aligned} J(w, b) &= \frac{1}{2m} \sum^{m}_{i=1} [f_{w,b}(x^{(i)}) - y^{(i)}]^2 \\ &= \frac{1}{2m} \sum^{m}_{i=1} [wx^{(i)} + b - y^{(i)}]^2 \end{aligned} J(w,b)=2m1i=1∑m[fw,b(x(i))−y(i)]2=2m1i=1∑m[wx(i)+b−y(i)]2
- 为什么需要乘以 1/2?因为对平方项求偏导后会出现系数 2,是为了约去这个系数。
梯度下降算法(gradient descent algorithm)
- α \alpha α:学习率(learning rate),用于控制梯度下降时的步长,以抵达损失函数的最小值处。若 α \alpha α 太小,梯度下降太慢;若 α \alpha α 太大,下降过程可能无法收敛。
- 梯度下降算法:
r e p e a t { t m p _ w = w − α ∂ J ( w , b ) w t m p _ b = b − α ∂ J ( w , b ) b w = t m p _ w b = t m p _ b } u n t i l c o n v e r g e \begin{aligned} repeat \{ \\ & tmp\_w = w - \alpha \frac{\partial J(w, b)}{w} \\ & tmp\_b = b - \alpha \frac{\partial J(w, b)}{b} \\ & w = tmp\_w \\ & b = tmp\_b \\ \} until \ & converge \end{aligned} repeat{}until tmp_w=w−αw∂J(w,b)tmp_b=b−αb∂J(w,b)w=tmp_wb=tmp_bconverge
其中,偏导数为
∂ J ( w , b ) w = 1 m ∑ i = 1 m [ f w , b ( x ( i ) ) − y ( i ) ] x ( i ) ∂ J ( w , b ) b = 1 m ∑ i = 1 m [ f w , b ( x ( i ) ) − y ( i ) ] \begin{aligned} & \frac{\partial J(w, b)}{w} = \frac{1}{m} \sum^{m}_{i=1} [f_{w,b}(x^{(i)}) - y^{(i)}] x^{(i)} \\ & \frac{\partial J(w, b)}{b} = \frac{1}{m} \sum^{m}_{i=1} [f_{w,b}(x^{(i)}) - y^{(i)}] \end{aligned} w∂J(w,b)=m1i=1∑m[fw,b(x(i))−y(i)]x(i)b∂J(w,b)=m1i=1∑m[fw,b(x(i))−y(i)]
参数(parameter)和超参数(hyperparameter)
- 超参数(hyperparameter):训练之前人为设置的任何数量都是超参数,例如学习率 α \alpha α
- 参数(parameter):模型在训练过程中创建或修改的任何数量都是参数,例如 w , b w, b w,b
代码实现样例
import numpy as np
import matplotlib.pyplot as plt# 计算误差均方函数 J(w,b)
def cost_function(x, y, w, b):m = x.shape[0] # 训练集的数据样本数cost_sum = 0.0for i in range(m):f_wb = w * x[i] + bcost = (f_wb - y[i]) ** 2cost_sum += costreturn cost_sum / (2 * m)# 计算梯度值 dJ/dw, dJ/db
def compute_gradient(x, y, w, b):m = x.shape[0] # 训练集的数据样本数d_w = 0.0d_b = 0.0for i in range(m):f_wb = w * x[i] + bd_wi = (f_wb - y[i]) * x[i]d_bi = (f_wb - y[i])d_w += d_wid_b += d_bidj_dw = d_w / mdj_db = d_b / mreturn dj_dw, dj_db# 梯度下降算法
def linear_regression(x, y, w, b, learning_rate=0.01, epochs=1000):J_history = [] # 记录每次迭代产生的误差值for epoch in range(epochs):dj_dw, dj_db = compute_gradient(x, y, w, b)# w 和 b 需同步更新w = w - learning_rate * dj_dwb = b - learning_rate * dj_dbJ_history.append(cost_function(x, y, w, b)) # 记录每次迭代产生的误差值return w, b, J_history# 绘制线性方程的图像
def draw_line(w, b, xmin, xmax, title):x = np.linspace(xmin, xmax)y = w * x + b# plt.axis([0, 10, 0, 50]) # xmin, xmax, ymin, ymaxplt.xlabel("X-axis", size=15)plt.ylabel("Y-axis", size=15)plt.title(title, size=20)plt.plot(x, y)# 绘制散点图
def draw_scatter(x, y, title):plt.xlabel("X-axis", size=15)plt.ylabel("Y-axis", size=15)plt.title(title, size=20)plt.scatter(x, y)# 从这里开始执行
if __name__ == '__main__':# 训练集样本x_train = np.array([1, 2, 3, 5, 6, 7])y_train = np.array([15.5, 19.7, 24.4, 35.6, 40.7, 44.8])w = 0.0 # 权重b = 0.0 # 偏置epochs = 10000 # 迭代次数learning_rate = 0.01 # 学习率J_history = [] # # 记录每次迭代产生的误差值w, b, J_history = linear_regression(x_train, y_train, w, b, learning_rate, epochs)print(f"result: w = {w:0.4f}, b = {b:0.4f}") # 打印结果# 绘制迭代计算得到的线性回归方程plt.figure(1)draw_line(w, b, 0, 10, "Linear Regression")plt.scatter(x_train, y_train) # 将训练数据集也表示在图中plt.show()# 绘制误差值的散点图plt.figure(2)x_axis = list(range(0, 10000))draw_scatter(x_axis, J_history, "Cost Function in Every Epoch")plt.show()运行结果


相关文章:

【机器学习】单变量线性回归
文章目录 线性回归模型(linear regression model)损失/代价函数(cost function)——均方误差(mean squared error)梯度下降算法(gradient descent algorithm)参数(parame…...

《计算思维导论》笔记:10.4 关系模型-关系运算
《大学计算机—计算思维导论》(战德臣 哈尔滨工业大学) 《10.4 关系模型-关系运算》 一、引言 本章介绍数据库的基本数据模型:关系模型-关系运算。 二、什么是关系运算 在数据库理论中,关系运算(Relational Operatio…...
)
QT+OSG/osgEarth编译之八十四:osgdb_osg+Qt编译(一套代码、一套框架,跨平台编译,版本:OSG-3.6.5插件库osgdb_osg)
文章目录 一、osgdb_osg介绍二、文件分析三、pro文件四、编译实践一、osgdb_osg介绍 osgDB是OpenSceneGraph(OSG)库中的一个模块,用于加载和保存3D场景数据。osgDB_osg是osgDB模块中的一个插件,它提供了对OSG格式的支持。 OSG格式是OpenSceneGraph库使用的一种二进制文件…...

【Redis快速入门】初识Redis、Redis安装、图形化界面
个人名片: 🐼作者简介:一名大三在校生,喜欢AI编程🎋 🐻❄️个人主页🥇:落798. 🐼个人WeChat:hmmwx53 🕊️系列专栏:🖼️…...
Linux(Ubuntu) 环境搭建:Nginx
注:服务器默认以root用户登录 NGINX 官方网站地址:https://nginx.org/en/NGINX 官方安装文档地址:https://nginx.org/en/docs/install.html服务器的终端中输入以下指令: # 安装 Nginx apt-get install nginx # 查看版本信息 ngi…...

快速手动完成 VS 编写脚本自动化:如何选取最高效的工作方式?
那些不懂技术的朋友们可能会觉得,写代码写脚本不就是敲敲键盘嘛,搞那么高科技做什么,直接手工点点鼠标不就完事了。 这种看法很常见,但实际情况要复杂得多。 首先,手工操作虽然对于短期和小规模的任务来说似乎更快&am…...

FAST角点检测算法
FAST(Features from Accelerated Segment Test)角点检测算法是一种快速且高效的角点检测方法。它通过检测每个像素周围的连续像素集合,确定是否为角点。以下是 FAST 角点检测算法的基本流程: FAST 角点检测算法的基本过程主要包括…...
Python中使用opencv-python进行人脸检测
Python中使用opencv-python进行人脸检测 之前写过一篇VC中使用OpenCV进行人脸检测的博客。以数字图像处理中经常使用的lena图像为例,如下图所示: 使用OpenCV进行人脸检测十分简单,OpenCV官网给了一个Python人脸检测的示例程序,…...

牛客网 DP3跳台阶扩展问题
在原始跳台阶问题上,我们知道只走1,2阶台阶的话,可以推出来斐波那契数列的形式进行计算操作。但是,在这里就是1,2,3,...n阶台阶了。其实思路是一样的。 在原始台阶问题,我们的状态方…...

ARM汇编[1] 打印格式化字符串(printf
文章目录 写在前面关键知识简单加减乘除函数调用和循环系统调用栈的使用 GDB调试示例代码 写在前面 如果您对ARM汇编还一无所知的话请先参考ARM汇编hello world 本篇不会广泛详细的列举各种指令,仍然只讲解最关键的部分,然后使用他们来完成一个汇编程序…...
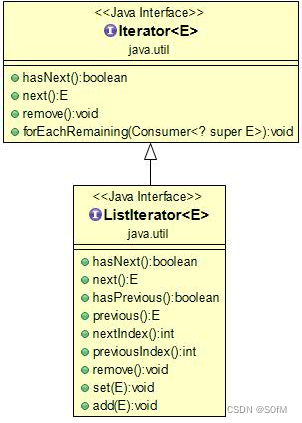
Java 集合、迭代器
Java 集合框架主要包括两种类型的容器,一种是集合(Collection),存储一个元素集合,另一种是图(Map),存储键/值对映射。Collection 接口又有 3 种子类型,List、Set 和 Queu…...
在 Docker 中启动 ROS2 里的 rivz2 和 rqt 出现错误的解决方法
1. 出现错误: 运行 ros2 run rivz2 rivz2 ,报错如下 : No protocol specified qt.qpa.xcb: could not connect to display :1 qt.qpa.plugin: Could not load the Qt platform plugin "xcb" in "" even though it was f…...
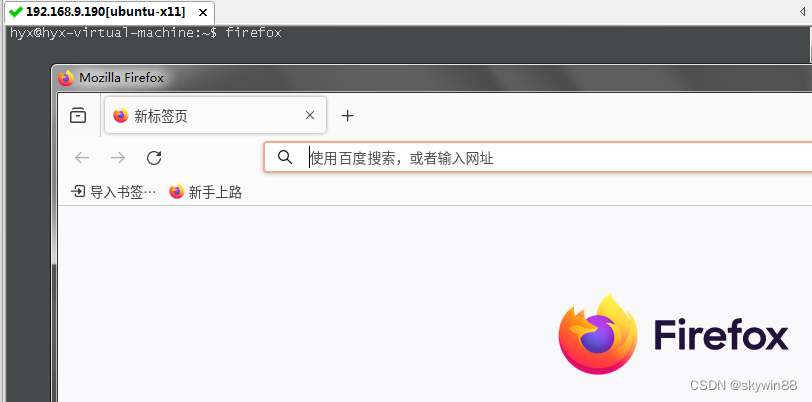
使用securecrt+xming通过x11访问ubuntu可视化程序
windows使用securecrtxming通过x11访问ubuntu可视化程序 windows机器IP:192.168.9.133 ubuntu-desktop20.04机器IP:192.168.9.190 windows下载xming并安装 按照图修改xming配置 开始->xming->Xlaunch 完成xming会在右下角后台运行 windows在…...
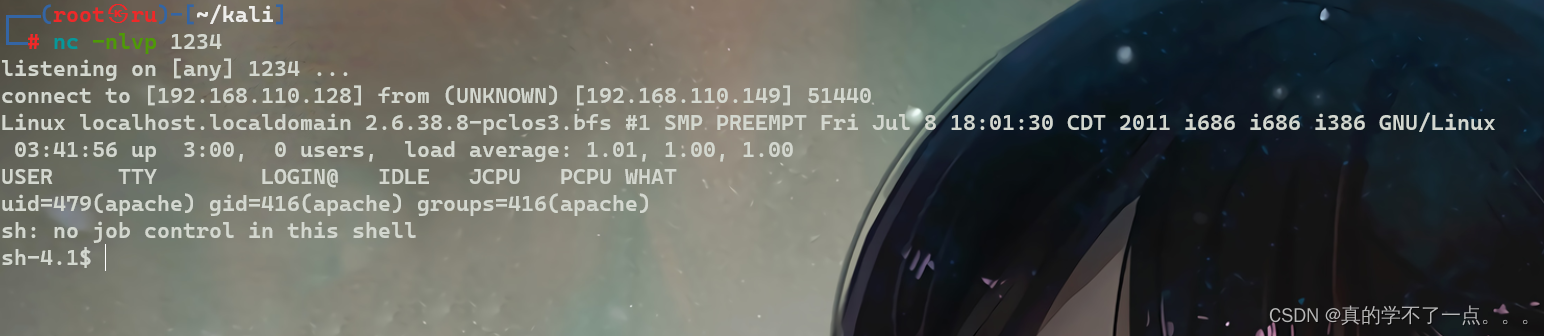
红队打靶练习:HEALTHCARE: 1
目录 信息收集 1、arp 2、nmap 3、nikto 4、whatweb 目录探测 1、gobuster 2、dirsearch WEB web信息收集 gobuster cms sqlmap 爆库 爆表 爆列 爆字段 FTP 提权 信息收集 本地提权 信息收集 1、arp ┌──(root㉿ru)-[~/kali] └─# arp-scan -l Inte…...

Java IO:概念和分类总结
前言 大家好,我是chowley,刚看完Java IO方面内容,特此总结一下。 Java IO Java IO(输入输出)是Java编程中用于处理输入和输出的API。它提供了一套丰富的类和方法,用于读取和写入数据到不同的设备、文件和…...
)
【Linux】基本命令(下)
目录 head指令 && tail指令 head指令 tail指令 find指令 grep指令 zip/unzip指令 tar指令 时间相关的指令 date显示 1.在显示方面,使用者可以设定欲显示的格式,格式设定为一个加号后接数个标记,其中常用的标记列表如下&…...

腾讯云游戏联机服务器配置价格表,4核16G/8核32G/4核32G/16核64G
2024年更新腾讯云游戏联机服务器配置价格表,可用于搭建幻兽帕鲁、雾锁王国等游戏服务器,游戏服务器配置可选4核16G12M、8核32G22M、4核32G10M、16核64G35M、4核16G14M等配置,可以选择轻量应用服务器和云服务器CVM内存型MA3或标准型SA2实例&am…...
面试经典150题——长度最小的子数组
"In the midst of winter, I found there was, within me, an invincible summer." - Albert Camus 1. 题目描述 2. 题目分析与解析 首先理解题意,题目要求我们找到一个长度最小的 连续子数组 满足他们的和大于target,需要返回的是子数组的…...

业务流程
一、需求分析和设计: 在项目启动阶段,需要与业务人员和产品经理充分沟通,了解业务需求,并根据需求进行系统设计和数据库设计。这一阶段的输出通常是需求文档、系统架构设计、数据库设计等。 1.需求文档 需求文档是一份非常重要…...
ChatGPT Plus如何升级?信用卡付款失败怎么办?如何使用信用卡升级 ChatGPT Plus?
ChatGPT Plus是OpenAI提供的一种高级服务,它相较于标准版本,提供了更快的响应速度、更强大的功能,并且用户可以优先体验到新推出的功能。 尽管许多用户愿意支付 20 美元的月费来订阅 GPT-4,但在实际支付过程中,特别是…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...
