【算法】{画决策树 + dfs + 递归 + 回溯 + 剪枝} 解决排列、子集问题(C++)
文章目录
- 1. 前言
- 2. 算法例题 理解思路、代码
- 46.全排列
- 78.子集
- 3. 算法题练习
- 1863.找出所有子集的异或总和再求和
- 47.全排列II
- 17.电话号码的字母组合
1. 前言
- dfs问题 我们已经学过,对于排列、子集类的问题,一般可以想到暴力枚举,但此类问题用暴力解法 一般都会超时,时间开销过大。
- 对于该种问题,重点在于尽可能详细的 画决策树,随后根据决策树分析 题目所涉及的 剪枝、回溯、递归等细节问题。
- 根据决策树的画法不同,题目会有不同的解法,只要保证决策树没有问题,保证细节问题下 代码一定可以编写出来。
2. 算法例题 理解思路、代码
46.全排列

思路
-
思路:求出数组中元素的所有排列顺序,并用数组输出。
-
解法一: 暴力枚举
- 用n层for循环,每层循环依次固定一个数
- 超时,时间开销太大,n个元素就是O(n ^ n)
-
解法二: 根据决策树 进行递归
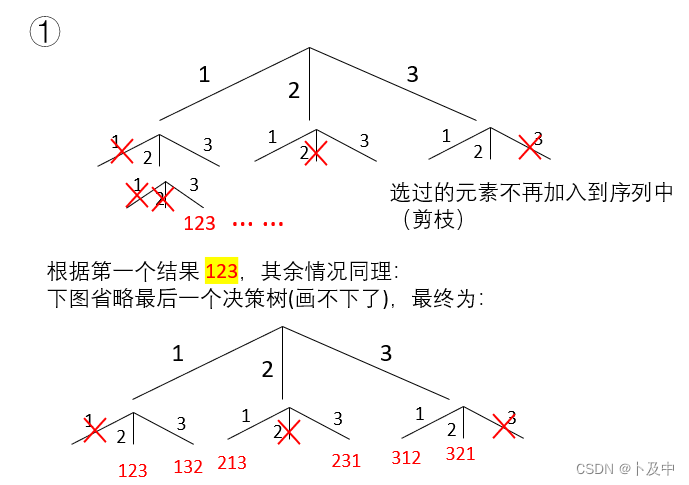
- 根据上图,我们需要创建下面三个全局变量.

- 结束条件:当我们遍历到叶子节点时(即
path.size() == nums.size()),将path加入到ret中,并向上返回。 - 回溯:对当前元素dfs后,进行回溯,回溯即将之前加入到path 的元素删除,并将used重新置为false。
- 根据上图,我们需要创建下面三个全局变量.
代码
class Solution {
public:vector<vector<int>> ret; // 用于存储最终结果bool used[7]; // 用于记录某个下标的元素是否在序列中vector<int> path; // 用于记录某个下标的元素是否已经加入到序列中vector<vector<int>> permute(vector<int>& nums) {dfs(nums);return ret;}void dfs(vector<int>& nums) {if(path.size() == nums.size()){ret.push_back(path);return;}// 遍历数组,对每一位都进行dfs && 排列for(int i = 0; i < nums.size(); ++i){if(used[i] == false) // 如果该位置未加入到当前序列中{path.push_back(nums[i]);used[i] = true;dfs(nums);// dfs向上返回回来 -> 回溯path.pop_back();used[i] = false;}}}
};
78.子集

- 题目要求我们将数组的所有子集统计,并以数组形式返回(空集就是空数组)
解法一
-
解法: 根据 选与不选 画决策树
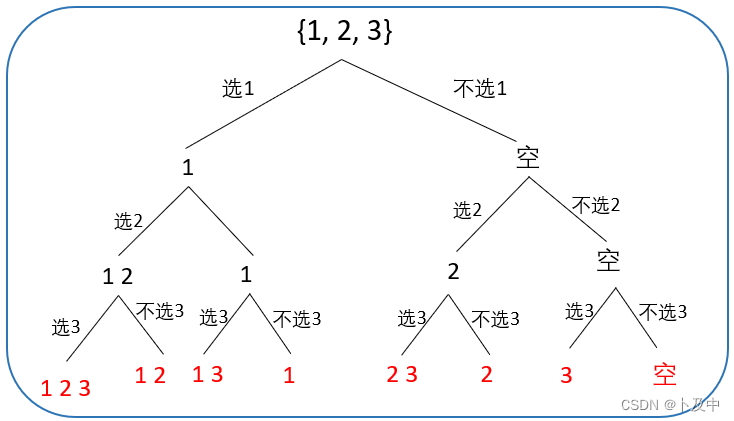
- 根据上图决策树,我们通过对一个元素的选择与否划分树,而当到达叶子节点的时候(
i == nums.size())向上返回即可。 - 函数头:首先需要的参数是数组本身,其次我们通过变量i来标记当前选择的元素所在层数,则
void dfs(vector<int>& nums, int i) - 函数体:分别写出选择与不选择该元素时的代码即可
- 结束条件:如前面所说,当 到叶子节点时返回。
- 根据上图决策树,我们通过对一个元素的选择与否划分树,而当到达叶子节点的时候(
代码
class Solution {
public:vector<vector<int>> ret;vector<int> path;vector<vector<int>> subsets(vector<int>& nums) {int i = 0;dfs(nums, i);return ret;}void dfs(vector<int>& nums, int i){if(i == nums.size()){ret.push_back(path);return;}// 不选当前元素dfs(nums, i + 1);// 选当前元素path.push_back(nums[i]);dfs(nums, i + 1);path.pop_back();}
};
解法二
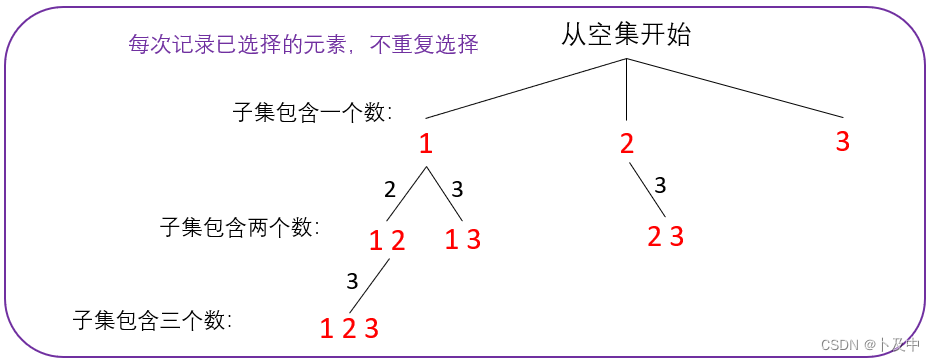
- 解法: 根据子集包含的元素个数 画 决策树
- 如上图所示,以此法画的决策树,每个节点的值都是有效值
- 函数头:第一个参数是数组本身,另外需要给出当前遍历到nums的第几个元素。
void dfs(vector<int>& nums, int pos) - 函数体:
- 在函数开始时先将当前子集加入到ret中
- 利用for循环,每次从pos开始遍历数组:每次将一个元素作为子集第一位的所有子集检索完毕后,再以下一个元素作为子集第一位,可以防止重复子集
- for循环中每次将当前元素加入到path中,dfs下一位,最后回溯
- 函数头:第一个参数是数组本身,另外需要给出当前遍历到nums的第几个元素。
代码
class Solution {
public:vector<vector<int>> ret;vector<int> path;vector<vector<int>> subsets(vector<int>& nums) {int pos = 0;dfs(nums, pos);return ret;}void dfs(vector<int>& nums, int pos){ret.push_back(path);for(int i = pos; i < nums.size(); ++i){path.push_back(nums[i]);dfs(nums, i + 1);path.pop_back(); // 回溯 - 恢复现场}}
};
3. 算法题练习
1863.找出所有子集的异或总和再求和

思路
- 题目分析:题目要求求出数组中所有子集的异或和的总和,我们只需要根据上图求子集的思路,在统计子集时,直接用变量计算异或值即可
- 解法: dfs + 决策树
- 这道题的决策树与上题一致,只需要在执行方面进行更改。
- 回溯:由于一个元素异或一个数两次,相当于没有异或,所以对于回溯操作,我们只需要再次进行异或即可。
- 解法: dfs + 决策树
代码
class Solution {
public:int ret = 0; // 最终结果int xorSum = 0; // 记录一个子集的异或和int subsetXORSum(vector<int>& nums) {dfs(nums, 0);return ret;}void dfs(vector<int>& nums, int pos){ret += xorSum;for(int i = pos; i < nums.size(); ++i){xorSum ^= nums[i];dfs(nums, i + 1);xorSum ^= nums[i]; // 回溯现场 / 异或同一个数两次相当于无异或}}
};
47.全排列II

思路
-
题目分析:

-
根据上图,制定决策树:
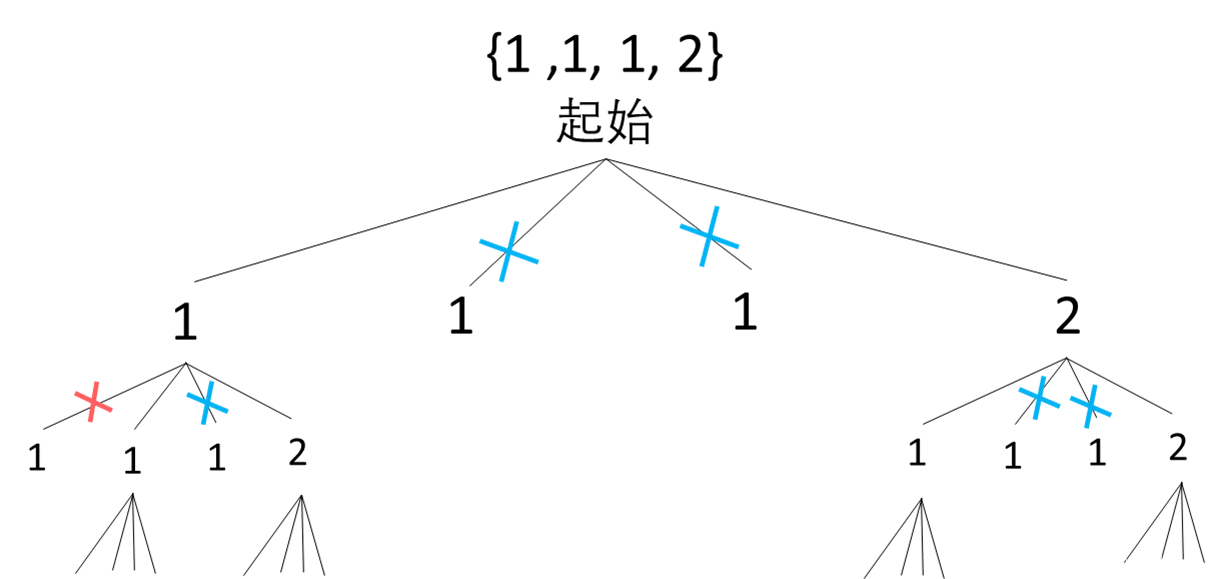
-
下面是对于上面决策树的解释,以及根据该决策树,我们如何设计代码:
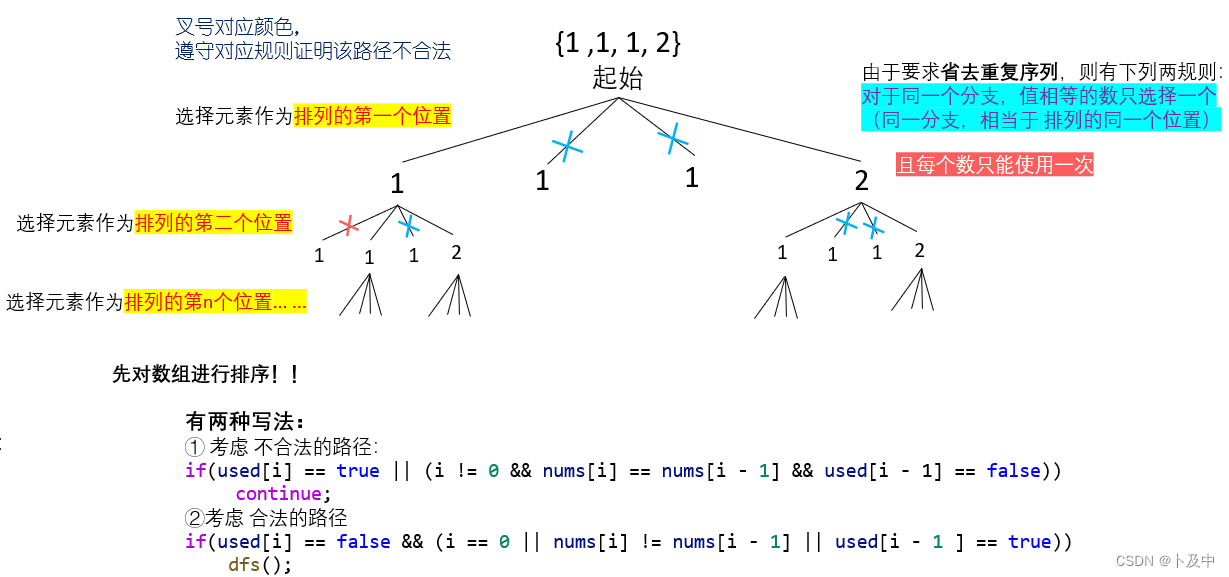
-
我们对上面探讨的两种解法进行解释:
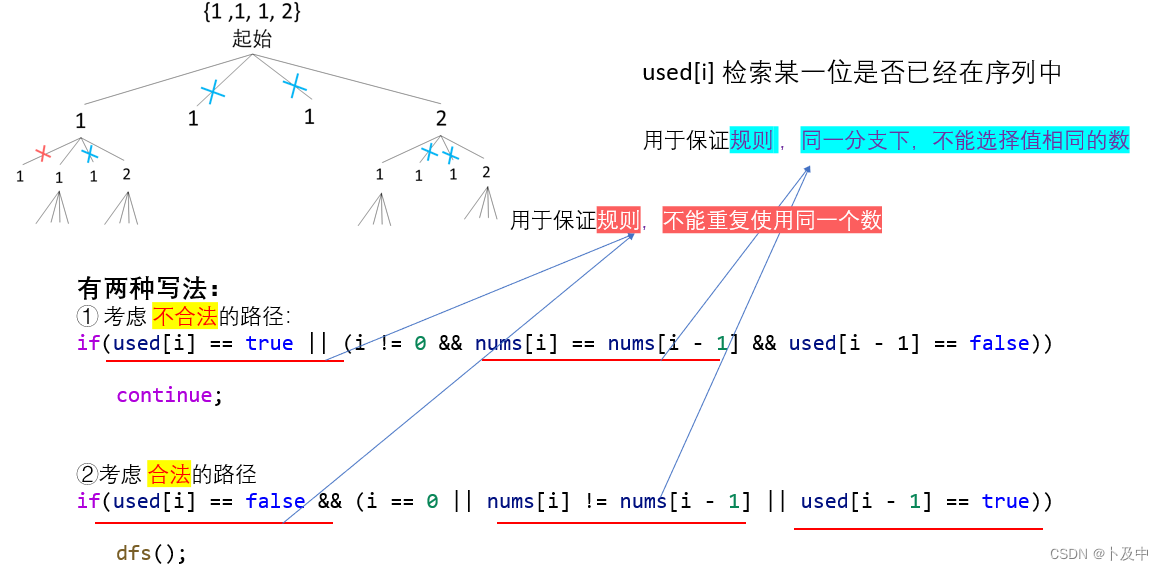
- 如图所示,如果用文字解释,对于不合法路径:
- 当 【当前元素A已经使用了 && 该分支下已有与当前元素值相同的B && B已经在序列中】时不合法。
- 如图所示,如果用文字解释,对于不合法路径:
-
编写代码方面,本道题与前面的题非常类似,主要在于主逻辑的差别:
代码
class Solution {
public:vector<vector<int>> ret;vector<int> path;bool used[9];vector<vector<int>> permuteUnique(vector<int>& nums) {sort(nums.begin(), nums.end()); // 先排序数组dfs(nums, 0);return ret;}void dfs(vector<int> nums, int pos){if(path.size() == nums.size()){ret.push_back(path);return;}for(int i = 0; i < nums.size(); ++i){// 剪枝 - 考虑合法路径if(used[i] == false && (i == 0 || nums[i] != nums[i - 1] || used[i - 1] == true)){path.push_back(nums[i]);used[i] = true;dfs(nums, pos + 1);path.pop_back();used[i] = false;}}}
};
17.电话号码的字母组合
思路

- 解法: dfs + 决策树
- 决策树:如下图所示

- 本体决策树画出来后,递归回溯等部分相对于前面简单一些
- 细节问题:
- 我们需要由数字与字符串一一对应来进行号码的模拟,这里可以用哈希表 ——> 优化:数组作为哈希表hash
- 主逻辑:关于for循环,我们需要从digits中依次提取数字字符,并找到相对应的字符串,即
hash[digits[pos] - '0']
- 细节问题:
代码
class Solution {
public:// 数组作哈希,下标对应字符串string hash[10] = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};string path;vector<string> ret;vector<string> letterCombinations(string digits) {// 特殊情况if(digits.size() == 0) return ret;dfs(digits, 0);return ret;}void dfs(string& digits, int pos) {if(path.size() == digits.size()){ret.push_back(path);return;}for(char ch : hash[digits[pos] - '0']) // 提取数字字符{path.push_back(ch);dfs(digits, pos + 1);path.pop_back();}}
};
有待更新… …
相关文章:

【算法】{画决策树 + dfs + 递归 + 回溯 + 剪枝} 解决排列、子集问题(C++)
文章目录 1. 前言2. 算法例题 理解思路、代码46.全排列78.子集 3. 算法题练习1863.找出所有子集的异或总和再求和47.全排列II17.电话号码的字母组合 1. 前言 dfs问题 我们已经学过,对于排列、子集类的问题,一般可以想到暴力枚举,但此类问题用…...

sqlserver 存储过程
在 SQL Server 中,存储过程(Stored Procedure)是一种预编译的 SQL 代码块,可以接受参数,执行一系列 SQL 语句,并返回一个或多个结果集。存储过程可以看作是一种封装了 SQL 语句的函数,可以在需要…...

C语言什么是悬空指针?
一、问题 什么是悬空指针?为什么会出现?我们该如何避免悬空指针的出现? 二、解答 在C语言中,悬空指针指的是指向已删除(或释放)的内存位置的指针。如果一个指针指向的内存被释放,但指针本身并未…...

AES加密后的密码可以破解吗
AES(高级加密标准)是一种广泛使用的对称加密算法,设计用来抵御各种已知的攻击方法。AES使用固定块大小的加密块和密钥长度,通常是128、192或256位。它被认为是非常安全的,到目前为止,没有已知的可行方法能够…...

vue3学习——路由进度条
安装 pnpm i nprogress创建permission.ts import router from /router/index.ts import NProgress from nprogress import nprogress/nprogress.css // 不加样式不显示 NProgress.configure({ showSpinner: false }) router.beforeEach((to, from, next) > {console.log(t…...

VMware虚拟机安装Windows系统教程
前言 今天给小伙伴分享一个安装Windows系统的教程,本教程适用于WindowsXP/7/8/8.1/10。 安装的系统前需要先检查一下你的电脑硬件环境,每个系统的硬件要求都不一样哦~ 硬件要求指的是你的电脑主机的配置,如果低于这个配置的&am…...

vue3学习——router-view 过渡动画
虽然vue3说建vue页面不用包裹一个根节点,但是transition不能没有唯一的标签 所以还是得包一层~ o( ̄▽ ̄)o <el-main><router-view v-slot"{ Component, route }"><transition name"MainFade" mode"o…...
从HSE攻击事件漫谈针对勒索攻击防御的两大误区
前言 HSE遭到严重的勒索软件攻击,爱尔兰的医疗服务系统是该国的公共资助医疗系统,在受到勒索病毒攻击之后,被迫在上周五关闭其 IT 系统,以此作为预防措施,避免威胁扩散。该事件导致该国家多家医院的服务取消和中断&am…...
外观模式)
设计模式(结构型模式)外观模式
目录 一、简介二、外观模式2.1、子系统2.2、外观类2.3、使用 三、优点与缺点 一、简介 外观模式(Facade Pattern)是一种结构型设计模式,提供了一个统一的接口,用于访问子系统中的一组接口。这个模式隐藏了子系统的复杂性ÿ…...

C语言函数的栈帧与销毁(面试亮点)
目录 如果你能熟练的掌握函数的栈帧与销毁在面试中是及其亮眼的加分项,所以我们来以实例来将解函数是如何实现栈帧与销毁的。 一. 函数栈帧 二.寄存器 三. 用例题讲解创建栈帧的过程 3.1 main 函数的反汇编代码。 第一步:给调用main函数的函数分配…...
实现 字符串动画)
使用 GreenSock(GSAP)实现 字符串动画
要使用 GreenSock(GSAP)实现 "JianMa XinXi" 这个字符串的动画,其中两个 x 字符自动旋转,j 和 m 字符上下跳动,并且美化这个字符串使其可以作为 logo 使用,我们可以通过以下步骤来实现࿱…...

linux系统zabbix监控服务端部署
zabbix服务端部署 zabbix服务端部署安装mysql创建初始数据库为Zabbix server配置数据库为Zabbix前端配置PHP启动Zabbix server和agent进程浏览器访问ipConfigure DB connection页面Zabbix server details页面登录账户名密码 zabbix 官网www.zabbix.com服务端部署 rpm -Uvh ht…...
)
算法----回溯(附录---剪枝)
回溯相信大家都已经了解了所以这章我将见但介绍下回溯剪枝 为什要剪枝 在《算法----回溯(正文)》中我提到过回溯就是暴力,为什么那些题能过,因为数据范围小 那如果数据范围大了,就不行了,这时剪枝的作用就…...
)
从Unity到Three.js(模型文件加载)
模型加载功能探索,用blender导出了个glb格式的cube进行的测试。 初接触js语法,回调注册的地方直接使用匿名函数总感觉脑子跟不上,反应不过来,就把加载后的回调简单封装了下, 官方文档是直接使用的匿名函数。 另外看官方…...

Webshell一句话木马
一、webshell介绍(网页木马) 分类: 大马:体积大、隐蔽性差、功能多 小马:体积小,隐蔽强,功能少 一句话木马:代码简短,灵活多样 二、一句话木马: :…...
【Web】Spring rce CVE-2022-22965漏洞复现学习笔记
目录 原理概览 漏洞简述 Tomcat AccessLogValve 和 access_log 例题: 原理概览 spring框架在传参的时候会与对应实体类自动参数绑定,通过“.”还可以访问对应实体类的引用类型变量。使用getClass方法,通过反射机制最终获取tomcat的日志配置成员属性…...

springboot/ssm大学生选修选课系统高校选课排课成绩管理系统Java系统
springboot/ssm大学生选修选课系统高校选课排课成绩管理系统Java系统 开发语言:Java 框架:springboot(可改ssm) vue JDK版本:JDK1.8(或11) 服务器:tomcat 数据库:my…...
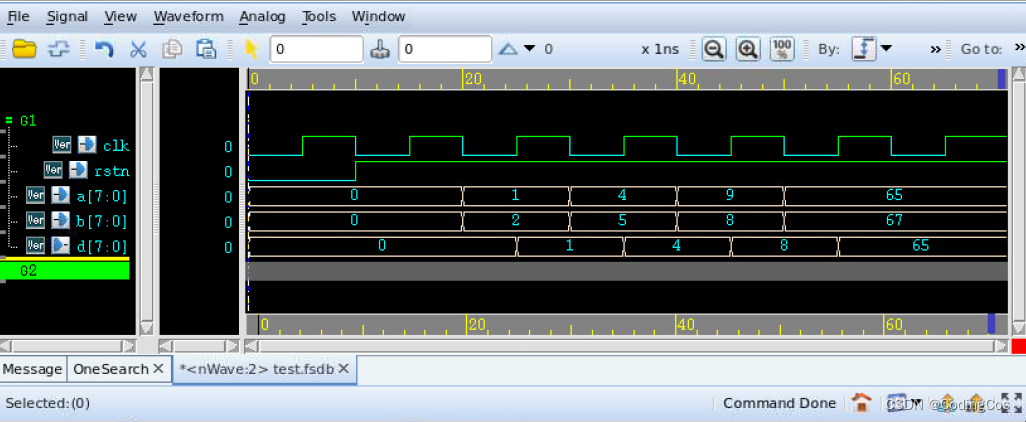
【芯片设计- RTL 数字逻辑设计入门 14 -- 使用子模块实现三输入数的大小比较】
文章目录 三输入数的大小比较问题分析verilog codeTestBench Code综合图仿真波形图 三输入数的大小比较 在数字芯片设计中,通常把完成特定功能且相对独立的代码编写成子模块,在需要的时候再在主模块中例化使用,以提高代码的可复用性和设计的层…...

Xilinx FPGA——在线升级
同以前单片机在线升级的做法一样,本质就是通信Flash操作跳转。 一、通信驱动 我使用的是UDP有线传输, 二、Flash芯片驱动 规划Flash芯片的区域,一般bootloader放在起始位置,APP放在bootloader之后的空白区域。 2.1 Flash擦除 我…...
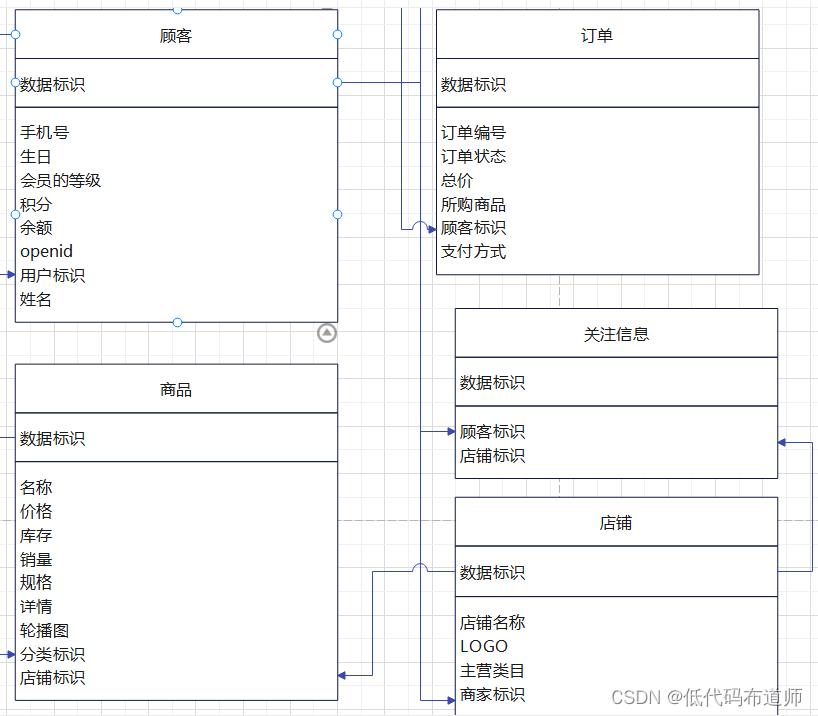
电商小程序02数据源设计
上一篇我们讲解了电商小程序的需求分析,分析了需要具备的功能并且绘制了系统原型。有了原型之后下一步的事情就是根据原型来设计数据源。 数据源就像盖房子打地基一样,地基打不好,楼可能就盖不高,盖起来要再想调整就比较困难。 …...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
