搜索专项---最短路模型
文章目录
- 迷宫问题
- 武士风度的牛
- 抓住那头牛
一、迷宫问题OJ链接
本题思路:只需要记录各个点是有哪个点走过来的,就能递推得出路径。记录前驱假设从 1,1 这个点向下走到了2, 1,则将2,1这个点的前驱记为1,1。这样,将整张地图 bfs 后,各个点的前驱就被记录了下来。输出路径:经过 bfs ,各个点的前驱已经被记录下来,我们只需要从终点开始,依次找当前节点的前驱,就能一直找到起点,从而得到一条路径。当然,这条路径是终点到起点的路径,倒序输出即为起点到终点的路径。如果 bfs 是从终点开始,则讲过上述步骤,得到的就是从起点到终点的路径,不用倒序输出。
#include <bits/stdc++.h>#define x first
#define y secondtypedef std::pair<int,int> PII;constexpr int N=1010;int n;
int g[N][N];
bool st[N][N];
PII pre[N][N];//储存当前位置的前驱位置
std::queue<PII> q;int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};void bfs(int ax,int ay)
{q.push({ax,ay});st[ax][ay]=true;while(!q.empty()){PII t=q.front();q.pop();for(int i=0;i<4;i++){int a=t.x+dx[i],b=t.y+dy[i];if(a<0||a>=n||b<0||b>=n) continue;if(g[a][b]) continue;if(!st[a][b]){q.push({a,b});pre[a][b]=t;st[a][b]=true;}}}}int main()
{std::ios::sync_with_stdio(false);std::cin.tie(nullptr);std::cout.tie(nullptr);std::cin>>n;for(int i=0;i<n;i++)for(int j=0;j<n;j++)std::cin>>g[i][j];bfs(n-1,n-1);//从终点位置进行遍历PII end(0,0);while (true){std::cout<<end.x<<" "<<end.y<<std::endl;if (end.x == n - 1 && end.y == n - 1) break;end = pre[end.x][end.y];}
}二、武士风度的牛OJ链接
本题题解: 从牛的起点,进行 bfs 即可。根据题意,牛走的是日字, 八个点。因此,dx, dy 和之前的四个点是不同的。可以得出:dx = [-2, -1, 1, 2, 2, 1, -1, -2],dy = [1, 2, 2, 1, -1, -2, -2, -1]
具体的:找到牛的起点,从起点开始进行 bfs向八个方向进行探索,判断这八个点是否合法:不越界和牛能走。对于合法的点,记录从起点走过来的距离,也就是上个点的距离+1。将合法的点放入队列。如果在 bfs过程中遇到了终点(干草) ,则返回答案。
#include <bits/stdc++.h>#define x first
#define y secondtypedef std::pair<int,int> PII;constexpr int N=2000;int n,m;
char g[N][N];
int dist[N][N];
std::queue<PII> q;int dx[8] = {-2, -1, 1, 2, 2, 1, -1, -2};
int dy[8] = {1, 2, 2, 1, -1, -2, -2, -1};int bfs(int ax,int ay)
{memset(dist,-1,sizeof dist);dist[ax][ay]=0;q.push({ax,ay});while(!q.empty()){PII t=q.front();q.pop();for(int i=0;i<8;i++){int a=t.x+dx[i],b=t.y+dy[i];if(a<0||a>=n||b<0||b>=m) continue;if(g[a][b]=='*') continue;if(dist[a][b]!=-1) continue;if(g[a][b]=='H') return dist[t.x][t.y]+1;dist[a][b]=dist[t.x][t.y]+1;q.push({a,b});}}}int main()
{std::ios::sync_with_stdio(false);std::cin.tie(nullptr);std::cout.tie(nullptr);std::cin>>m>>n;for(int i=0;i<n;i++) std::cin>>g[i];int ax,ay;for(int i=0;i<n;i++)for(int j=0;j<m;j++)if(g[i][j]=='K'){ax=i;ay=j;}std::cout<<bfs(ax,ay)<<std::endl;return 0;
}三、抓住那头牛OJ链接
本题思路: 这道题是一个一维的找最短路径的问题,无论+1,-1,* 2 花费都是1分钟,即权值相同, 所以才能用BFS去找最短路。假设当前点为t , 目标点为k出队扩展循环判断 1、如果t-1小于0了,那就不能走-1的方法 2、如果t+1 大于了N(10的5次方+10 ),就不能走+1的方法。 3、如果t * 2大于了N,也就不能走* 2的方法了。当然三个判断都应该加上此点是否被走过的条件,如果满足条件,就把其入队,出队时判断t是否等于k,如果相等就return距离。那么为什么N要取的比K大一点呢,因为先减1再乘2扩大会比先乘再减一缩小更快的接近K,1、当k为偶数,假设为100,当前点为51,那么减一再乘更快,2、当k为奇数,假设为99,当前点为50,那么先乘再减一时更快一点的。所以N要取的比K大一点,当超过N的时候就不会有这样的区别,一定是先减再乘可以更快的接近K。
#include <bits/stdc++.h>constexpr int N=1e5+10;int n,k;
int dist[N];
std::queue<int> q;int bfs()
{q.push(n);dist[n]=0;while(!q.empty()){auto t=q.front();q.pop();if(t==k) return dist[k];if(t-1>=0&&dist[t-1]==-1){q.push(t-1);dist[t-1]=dist[t]+1;}if(t+1<=N&&dist[t+1]==-1){q.push(t+1);dist[t+1]=dist[t]+1;}if(t*2<=N&&dist[t*2]==-1){q.push(t*2);dist[t*2]=dist[t]+1;}}
}int main()
{std::ios::sync_with_stdio(false);std::cin.tie(nullptr);std::cout.tie(nullptr);memset(dist,-1,sizeof dist);std::cin>>n>>k;std::cout<<bfs()<<std::endl;return 0;
}相关文章:

搜索专项---最短路模型
文章目录 迷宫问题武士风度的牛抓住那头牛 一、迷宫问题OJ链接 本题思路:只需要记录各个点是有哪个点走过来的,就能递推得出路径。记录前驱假设从 1,1 这个点向下走到了2, 1,则将2,1这个点的前驱记为1,1。这样,将整张地图 bfs 后,…...

安装PostgreSQL和PostGIS
安装环境 Windows 2019 Standard Server 安装PostgreSQL 安装PostgreSQL 16 安装PostGIS 用PostgreSQL 16对应的PostGIS https://download.osgeo.org/postgis/windows/pg16/ https://download.osgeo.org/postgis/windows/pg16/postgis-bundle-pg16x64-setup-3.4.1-1.exe 创建…...

MySQL-----DCL基础操作
▶ DCL简介 DCL英文全称是Data ControlLanguage(数据控制语言),用来管理数据库用户、控制数据库的访问权限。 DCL--管理用户 ▶ 查询用户 use mysql; select * from user; ▶ 创建用户 ▶ 语法 create user 用户名主机名 identified by 密码 设置为在任意主机上访问…...
 is not installed)
Unity报错Currently selected scripting backend (IL2CPP) is not installed
目录 什么是il2cpp il2cpp换mono Unity打包报错Currently selected scripting backend (IL2CPP) is not installed 什么是il2cpp Unity 编辑器模式下是采用.net 虚拟机解释执行.net 代码,发布的时候有两种模式,一种是mono虚拟机模式,一种是il2cpp模式。由于iOS AppStore…...

LeetCode79. Word Search——回溯
文章目录 一、题目二、题解 一、题目 Given an m x n grid of characters board and a string word, return true if word exists in the grid. The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertic…...
)
Linux命令-blkid命令(查看块设备的文件系统类型、LABEL、UUID等信息)
说明 在Linux下可以使用 blkid命令 对查询设备上所采用文件系统类型进行查询。blkid主要用来对系统的块设备(包括交换分区)所使用的文件系统类型、LABEL、UUID等信息进行查询。要使用这个命令必须安装e2fsprogs软件包。 语法 blkid -L | -U blkid [-c…...

服务治理中间件-Eureka
目录 简介 搭建Eureka服务 注册服务到Eureka 简介 Eureka是Spring团队开发的服务治理中间件,可以轻松在项目中,实现服务的注册与发现,相比于阿里巴巴的Nacos、Apache基金会的Zookeeper,更加契合Spring项目,缺点就是…...
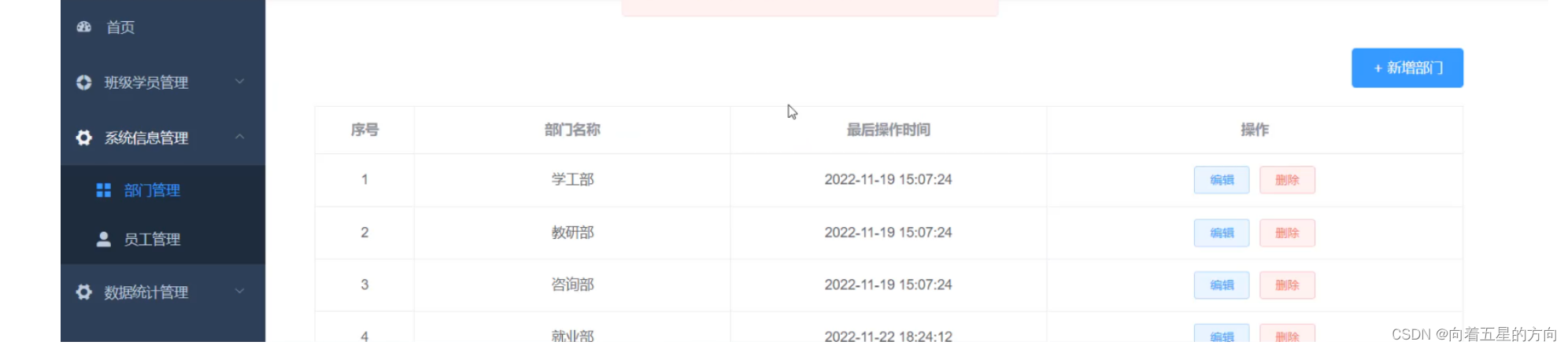
Javaweb之SpringBootWeb案例之异常处理功能的详细解析
3. 异常处理 3.1 当前问题 登录功能和登录校验功能我们都实现了,下面我们学习下今天最后一块技术点:异常处理。首先我们先来看一下系统出现异常之后会发生什么现象,再来介绍异常处理的方案。 我们打开浏览器,访问系统中的新增部…...

苹果Mac键盘如何将 F1 到 F12 取消按Fn
苹果电脑安装了Win10操作系统之后,F1到F12用不了怎么办的解决方法。本文将介绍一些解决方法,帮助您解决无法使用F1到F12功能键的问题。 使用 Mac系统的人都知道,Mac系统默认是没有开启 F1-F12 的使用的,平时我们使用的系统都可以使…...

linux下ipconfig命令报:command not found 解决方法
参考博文: linux下ipconfig命令报:command not found 解决方法 CentOS7更新yum报Could not resolve host:mirrorlist.centos.org; Unknown error解决办法...

Android导入其它项目慢,Gradel下载失败,另辟蹊径:使用离线gradle加载,附镜像方式
最近在开发中需要测试以前写的小项目。结果忘了换本地的gradle,提示下载失败。换了现在用的gradle,项目能跑了。虽然网上有很多很多教程了,但对我的情况也不是都适用。所以自己记录一下。本人水平有限,有不对的地方请帮我指正&…...
项目的15 个开源训练数据集)
神经语言程式(NLP)项目的15 个开源训练数据集
一个聊天机器人需要大量的训练数据,以便在无需人工干预的情况下快速解决用户的询问。然而,聊天机器人开发的主要瓶颈是获取现实的、面向任务的对话数据来训练这些基于机器学习的系统。 我们整理了训练聊天机器人所需的对话数据集,包括问答数据、客户支持数据、对话数据和多…...

H5 红色文字抖动网址发布页/引导页源码
H5 红色文字抖动网址发布页/引导页源码 源码介绍:一款红色文字抖动网页源码,可用于引导页或网址发布页。 下载地址: https://www.changyouzuhao.cn/10470.html...
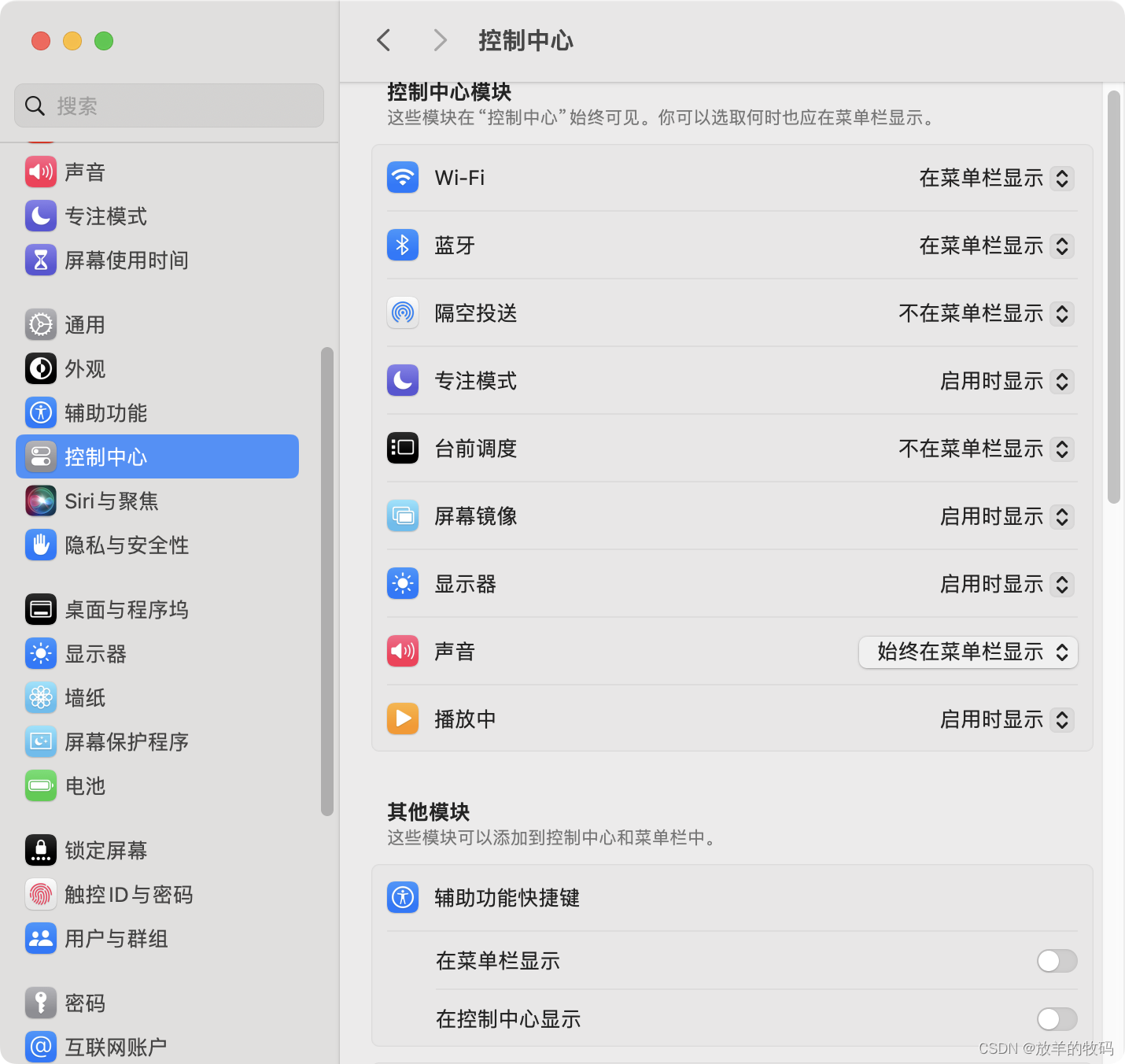
MacOS - 菜单栏上显示『音量』
教程步骤 点击打开系统偏好『设置』,并找到『控制中心』 在『控制中心模块』找到『声音』,选择『始终在菜单栏显示』...

深入理解常见的设计模式
目录 引言 1. 单例模式(Singleton Pattern) 应用场景: 示例代码: . 工厂模式(Factory Pattern) 应用场景: 示例代码: 3. 观察者模式(Observer Pattern)…...

服务器解析漏洞及任意文件下载
1.服务器文件解析漏洞 文件解析漏洞,是指Web容器(Apache、nginx、iis等)在解析文件时出现了漏洞,以其他格式执行出脚本格式的效果。从而,黑客可以利用该漏洞实现非法文件的解析。 (1) Apache linux系统中的apache的php配置文件在/etc/apac…...

ES6扩展运算符——三个点(...)用法详解
目录 1 含义 2 替代数组的 apply 方法 3 扩展运算符的应用 ( 1 )合并数组 ( 2 )与解构赋值结合 ( 3 )函数的返回值 ( 4 )字符串 ( 5 )实现了 Iter…...

限制资源使用
限制资源使用 您需要显示对服务器资源的访问来保护Web应用程序和应用程序数据不受未授权用户的访问。在Java EE Web应用程序中,您可以通过在应用服务器中创建用户和用户组来保护资源免受未经授权的访问。您可以为应用程序定义角色并在部署过程中将角色分配给用户。 1. 创建授权…...

结合Next项目实际认识webpack.splitChunks
本文的目的在于简单的介绍webpack的优化功能配置:splitChunks。 webpack5出于“开箱即用”的目的,将大部分曾经要使用插件的功能集成到了config配置中,因此用户只需要了解如何配置,即可达到优化目的,其中最常使用接触的…...
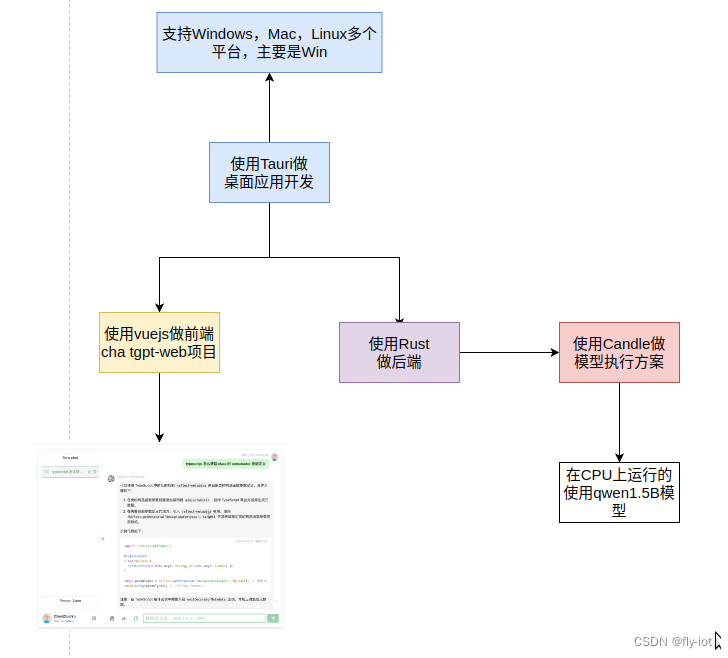
【Tauri】(2):使用Tauri应用开发,使用开源的Chatgpt-web应用做前端,使用rust 的candle做后端,本地运行小模型桌面应用
视频演示地址 https://www.bilibili.com/video/BV17j421X7Zc/ 【Tauri】(2):使用Tauri应用开发,使用开源的Chatgpt-web应用做前端,使用rust 的candle做后端,本地运行小模型桌面应用 1,做一个免…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...
