苹果Mac键盘如何将 F1 到 F12 取消按Fn
苹果电脑安装了Win10操作系统之后,F1到F12用不了怎么办的解决方法。本文将介绍一些解决方法,帮助您解决无法使用F1到F12功能键的问题。
使用 Mac系统的人都知道,Mac系统默认是没有开启 F1-F12 的使用的,平时我们使用的系统都可以使用键盘上的功能键,下面我们就可看看,如何设置才能使用 Mac 键盘上的功能键。
有时候打游戏或者用专业软件快捷键是F1~F12,但Mac键盘直接按就是亮度音量之类的功能,还得按住Fn才能实现F1~12的按键,挺不方便的。那么如何取消Fn键呢?具体的操作方法如下:
1、首先在系统桌面的左上角点击苹果图标,找到【系统偏好设置】,点击打开【系统偏好设置】面板,如图所示。
2、在打开的【系统偏好设置】面板里的【硬件】里找到【键盘】,点击它。
3、在打开的【键盘】面板里找到【键盘】,这里有【键盘】和【键盘快捷键】两项,如图所示。
4、在“键盘”选项里找到“将F1、F2”等键用作标准功能键,把它前面的勾选上,如图所示。
5、Mac 键盘如何开启 F1-F12 功能键设置完成。
其它版本Mac操作系统如何设置:
1、进入左上角苹果图标的【系统设置】;

2、左边栏向下到底,找到【键盘】,然后在当中找到【键盘快捷键】;

3、点进去之后发现没有,别着急,在新弹出窗口的左侧栏下方找到【Fn功能键】,然后开启里面的选项即可。

以上设置结束,功能好用。
Windows10系统下如何修改功能键设置
那么苹果电脑Mac系统改了Win10系统之后的Fn功能键如何设置呢?Win10系统Fn功能键的问题,您希望在 Boot Camp 中通过按下功能键和 Fn 键来实现功能。请您参考以下操作:
1、查看 Windows 桌面时,单击系统任务栏中的 Boot Camp 图标 ,然后选取“Boot Camp 控制面板”。如果在系统任务栏中未看到 Boot Camp 图标 ,请单击三角形来显示隐藏的图标。如果“用户帐户控制”对话框出现,请单击“是”。
2、单击“键盘”。
3、选择“将 F1、F2 等键用作标准功能键”。
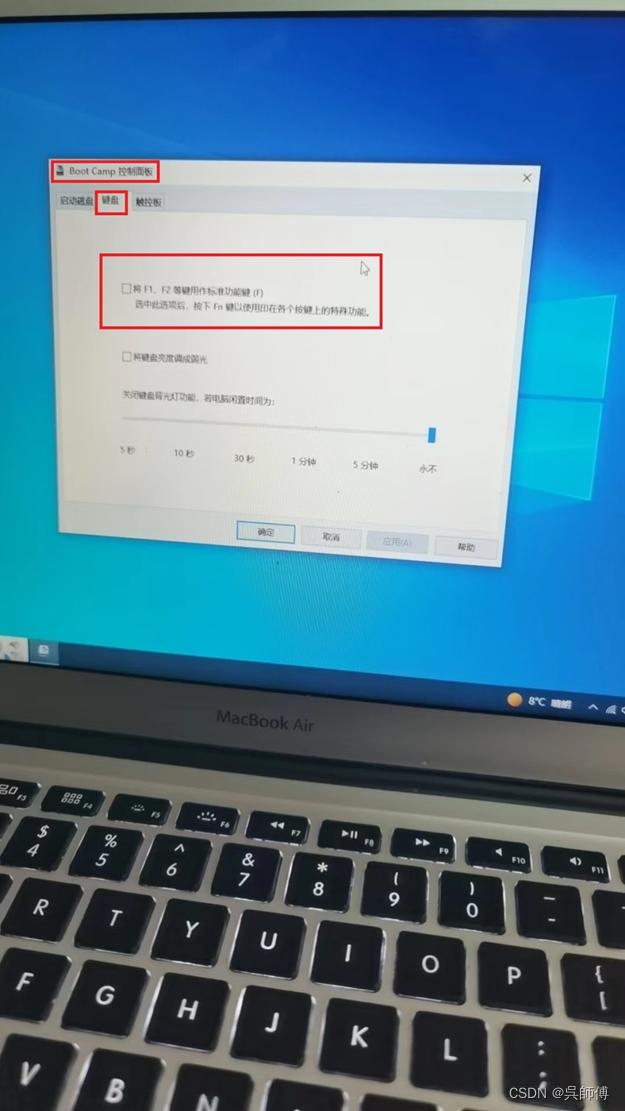
在 Apple 键盘上使用功能键
在 Windows 中,默认情况下按下便携式 Mac 和其他某些 Apple 键盘上的功能键可以控制硬件功能。Boot Camp 支持音量、亮度、键盘照明和媒体键。
若要控制应用功能,请按下功能键和 Fn 键。例如,如果您打开了 iTunes,那么按下 Fn-F1 将会打开“iTunes 帮助”。
在“Boot Camp 控制面板”中,您可以更改默认行为,即按下功能键来控制应用功能,按下功能键和 Fn 键来控制硬件功能。
1、如果您正在查看 Windows 8 启动屏幕,请单击“桌面”以查看 Windows 桌面。
2、查看 Windows 桌面时,单击系统任务栏中的 Boot Camp 图标 ,然后选取“Boot Camp 控制面板”。
如果在系统任务栏中未看到 Boot Camp 图标 ,请单击三角形来显示隐藏的图标。
3、如果“用户帐户控制”对话框出现,请单击“是”。
4、单击“键盘”。
5、选择或取消选择“将 F1、F2 等键用作标准功能键”。
某些便携式 Mac 电脑有一组标有小数字的按键,可将它们用作数字小键盘。若要将这些按键用作数字小键盘,请按下 Num Lock (F6) 键,或按住 Fn 键并按下键盘上的按键。
通过本文介绍的方法,用户可以尝试解决这一问题,并恢复F1到F12功能键的正常使用。如果问题仍然存在,建议用户联系苹果客服或专业技术人员寻求进一步的帮助。希望本文能对遇到类似问题的用户提供一些参考和帮助。
速印机(理想、理光、基士得耶、荣大等)、复印机(夏普、东芝、理光、佳能、震旦等全系列)、打印机、扫描仪、传真机、多媒体教学一体机、交互式电子白板、报警器材、监控、国产化设备、竞业达监考设备及其它监考设备、听力考试设备、特种安防设备维护及维修。

相关文章:

苹果Mac键盘如何将 F1 到 F12 取消按Fn
苹果电脑安装了Win10操作系统之后,F1到F12用不了怎么办的解决方法。本文将介绍一些解决方法,帮助您解决无法使用F1到F12功能键的问题。 使用 Mac系统的人都知道,Mac系统默认是没有开启 F1-F12 的使用的,平时我们使用的系统都可以使…...

linux下ipconfig命令报:command not found 解决方法
参考博文: linux下ipconfig命令报:command not found 解决方法 CentOS7更新yum报Could not resolve host:mirrorlist.centos.org; Unknown error解决办法...

Android导入其它项目慢,Gradel下载失败,另辟蹊径:使用离线gradle加载,附镜像方式
最近在开发中需要测试以前写的小项目。结果忘了换本地的gradle,提示下载失败。换了现在用的gradle,项目能跑了。虽然网上有很多很多教程了,但对我的情况也不是都适用。所以自己记录一下。本人水平有限,有不对的地方请帮我指正&…...
项目的15 个开源训练数据集)
神经语言程式(NLP)项目的15 个开源训练数据集
一个聊天机器人需要大量的训练数据,以便在无需人工干预的情况下快速解决用户的询问。然而,聊天机器人开发的主要瓶颈是获取现实的、面向任务的对话数据来训练这些基于机器学习的系统。 我们整理了训练聊天机器人所需的对话数据集,包括问答数据、客户支持数据、对话数据和多…...

H5 红色文字抖动网址发布页/引导页源码
H5 红色文字抖动网址发布页/引导页源码 源码介绍:一款红色文字抖动网页源码,可用于引导页或网址发布页。 下载地址: https://www.changyouzuhao.cn/10470.html...
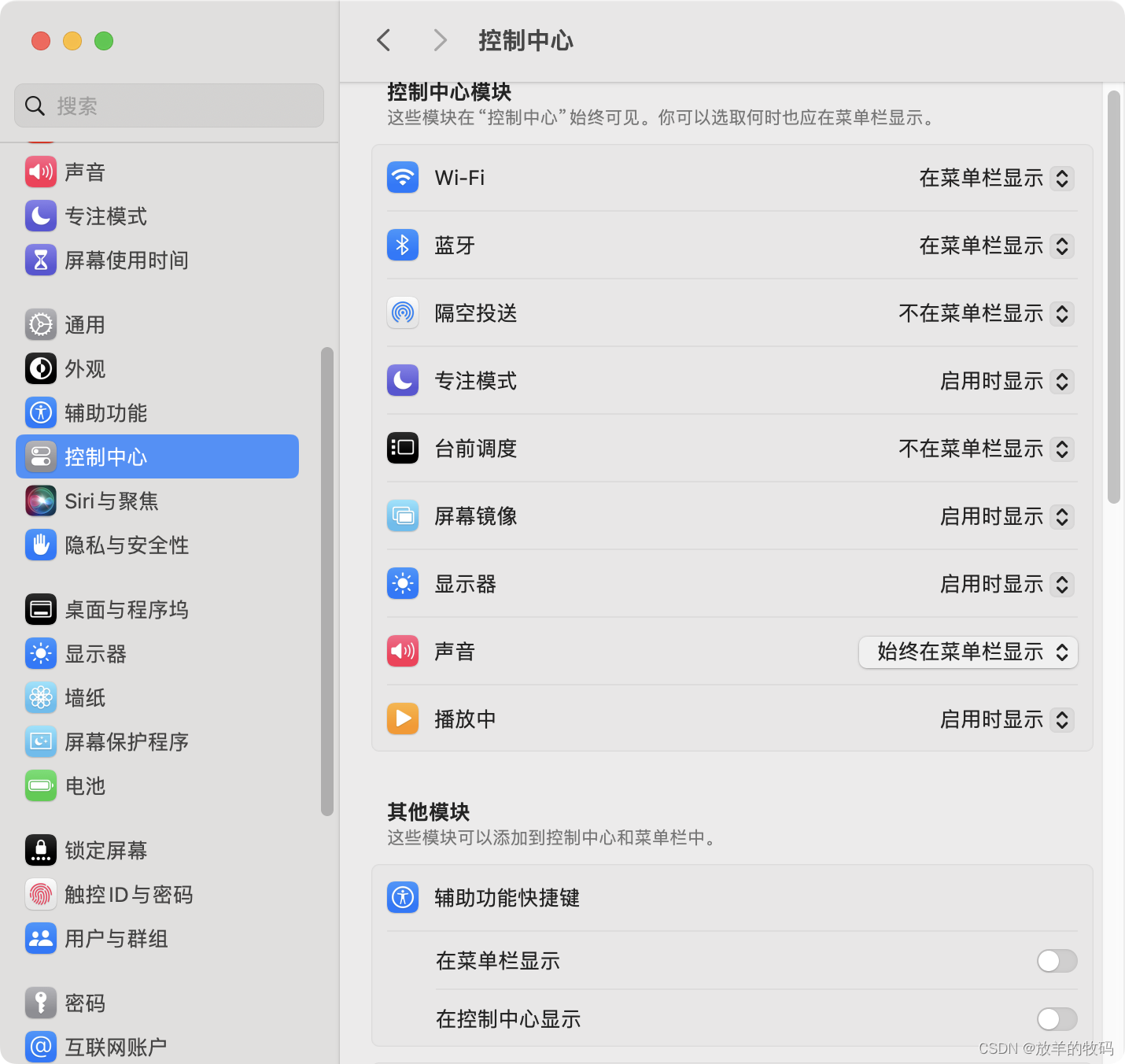
MacOS - 菜单栏上显示『音量』
教程步骤 点击打开系统偏好『设置』,并找到『控制中心』 在『控制中心模块』找到『声音』,选择『始终在菜单栏显示』...

深入理解常见的设计模式
目录 引言 1. 单例模式(Singleton Pattern) 应用场景: 示例代码: . 工厂模式(Factory Pattern) 应用场景: 示例代码: 3. 观察者模式(Observer Pattern)…...

服务器解析漏洞及任意文件下载
1.服务器文件解析漏洞 文件解析漏洞,是指Web容器(Apache、nginx、iis等)在解析文件时出现了漏洞,以其他格式执行出脚本格式的效果。从而,黑客可以利用该漏洞实现非法文件的解析。 (1) Apache linux系统中的apache的php配置文件在/etc/apac…...

ES6扩展运算符——三个点(...)用法详解
目录 1 含义 2 替代数组的 apply 方法 3 扩展运算符的应用 ( 1 )合并数组 ( 2 )与解构赋值结合 ( 3 )函数的返回值 ( 4 )字符串 ( 5 )实现了 Iter…...

限制资源使用
限制资源使用 您需要显示对服务器资源的访问来保护Web应用程序和应用程序数据不受未授权用户的访问。在Java EE Web应用程序中,您可以通过在应用服务器中创建用户和用户组来保护资源免受未经授权的访问。您可以为应用程序定义角色并在部署过程中将角色分配给用户。 1. 创建授权…...

结合Next项目实际认识webpack.splitChunks
本文的目的在于简单的介绍webpack的优化功能配置:splitChunks。 webpack5出于“开箱即用”的目的,将大部分曾经要使用插件的功能集成到了config配置中,因此用户只需要了解如何配置,即可达到优化目的,其中最常使用接触的…...
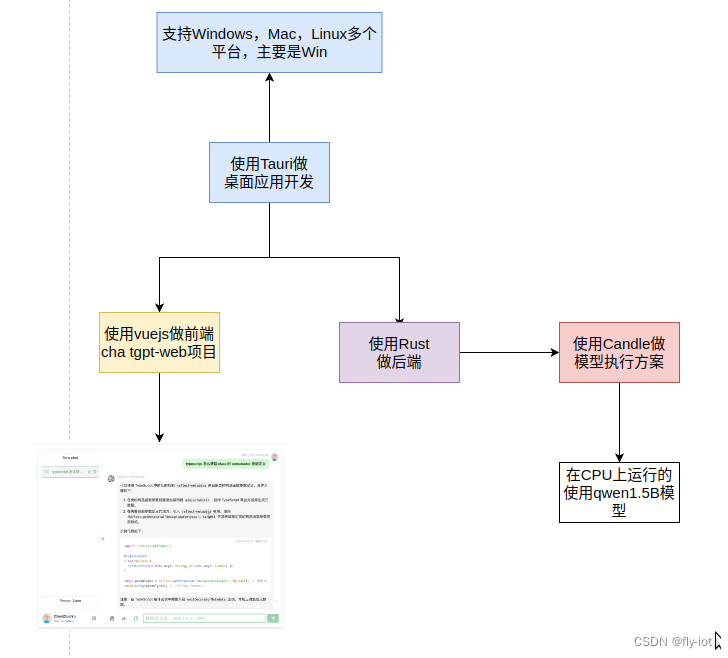
【Tauri】(2):使用Tauri应用开发,使用开源的Chatgpt-web应用做前端,使用rust 的candle做后端,本地运行小模型桌面应用
视频演示地址 https://www.bilibili.com/video/BV17j421X7Zc/ 【Tauri】(2):使用Tauri应用开发,使用开源的Chatgpt-web应用做前端,使用rust 的candle做后端,本地运行小模型桌面应用 1,做一个免…...
语法)
C#where T :通用的泛型约束(generic constraint)语法
在C#中,where T :是一种通用的泛型约束(generic constraint)语法,用于限制泛型类型参数T的特定条件。通过使用泛型约束,我们可以对泛型类型参数进行更具体的限制,以确保在使用泛型时满足特定的要求。 wher…...
使用hls.js)
vue使用Mars3d弹框嵌套video视频/实时视频(m3u8)使用hls.js
下载hls.js http://mars3d.cn/lib/video/hls/hls.js下载 1.首先绘制地图我使用的天地图 async infoMars3d() {const that this;var mapOptions {scene: {center: {lat: 30.435192,lng: 103.936535,alt: 200000,heading: 359,pitch: -79},highDynamicRange: false},// 方式1&a…...
Python爬虫之Ajax数据爬取基本原理
前言 有时候我们在用 requests 抓取页面的时候,得到的结果可能和在浏览器中看到的不一样:在浏览器中可以看到正常显示的页面数据,但是使用 requests 得到的结果并没有。这是因为 requests 获取的都是原始的 HTML 文档,而浏览器中…...

osg操控器和键盘切换操控器学习
osg提供了很多操控器,在src\osgGA目录下,cpp文件名含有Manipulator的都是操控器,每个这样的cpp表示一种类型的操控器。 名字带 Manipulator 的类都是操控器; 其中KeySwitchMatrixManipulator.cpp文件实现了键盘切换操控器; 操控器是指:操控相机运动,从而实现场景视图…...

LeetCode1143. Longest Common Subsequence——动态规划
文章目录 一、题目二、题解 一、题目 Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0. A subsequence of a string is a new string generated from the original string with so…...
利用Windows10漏洞破解密码(保姆级教学)
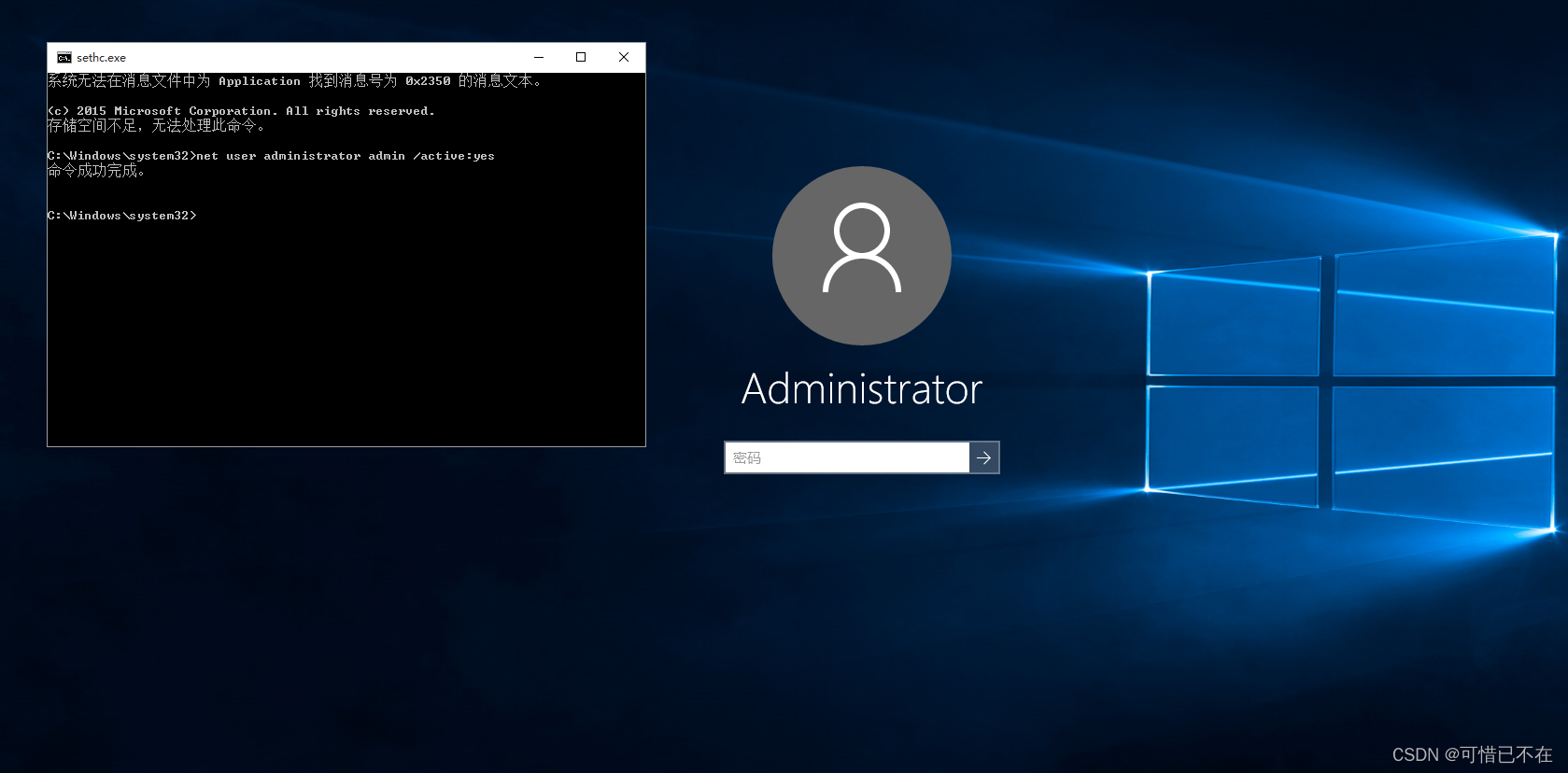
前言: 本篇博客只是技术分享并非非法传播知识,实验内容均是在虚拟机中进行,并非真实环境 正文: 一.windows10电脑密码破解 1)开启windows10虚拟机,停留在这个页面 2)按5次Shift键,出现这个粘滞键,如果没有出现的,则说明漏洞已经修复 3)重新启动,在这个页面的时候…...

apk反编译修改教程系列---简单修改apk默认横竖屏显示 手机端与电脑端同步演示【十一】
往期教程: apk反编译修改教程系列-----修改apk应用名称 任意修改名称 签名【一】 apk反编译修改教程系列-----任意修改apk版本号 版本名 防止自动更新【二】 apk反编译修改教程系列-----修改apk中的图片 任意更换apk桌面图片【三】 apk反编译修改教程系列---简单…...

2301: 不定方程解的个数
题目描述 输出不定方程解的个数。在数学中,不定方程是数论中的一个重要课题,在各种比赛中也常常出现. 对于不定方程,有时我们往往只求非负整数解,现有方程axbyc0,其中x、y为未知量且不超过10000,当给定a、…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...
