LeetCode1143. Longest Common Subsequence——动态规划
文章目录
- 一、题目
- 二、题解
一、题目
Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0.
A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
For example, “ace” is a subsequence of “abcde”.
A common subsequence of two strings is a subsequence that is common to both strings.
Example 1:
Input: text1 = “abcde”, text2 = “ace”
Output: 3
Explanation: The longest common subsequence is “ace” and its length is 3.
Example 2:
Input: text1 = “abc”, text2 = “abc”
Output: 3
Explanation: The longest common subsequence is “abc” and its length is 3.
Example 3:
Input: text1 = “abc”, text2 = “def”
Output: 0
Explanation: There is no such common subsequence, so the result is 0.
Constraints:
1 <= text1.length, text2.length <= 1000
text1 and text2 consist of only lowercase English characters.
二、题解
class Solution {
public:int longestCommonSubsequence(string text1, string text2) {int n = text1.size(),m = text2.size();vector<vector<int>> dp(n+1,vector<int>(m+1,0));for(int i = 1;i <= n;i++){for(int j = 1;j <= m;j++){if(text1[i - 1] == text2[j - 1]) dp[i][j] = 1 + dp[i-1][j-1];else dp[i][j] = max(dp[i-1][j],dp[i][j-1]);}}return dp[n][m];}
};
相关文章:

LeetCode1143. Longest Common Subsequence——动态规划
文章目录 一、题目二、题解 一、题目 Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0. A subsequence of a string is a new string generated from the original string with so…...
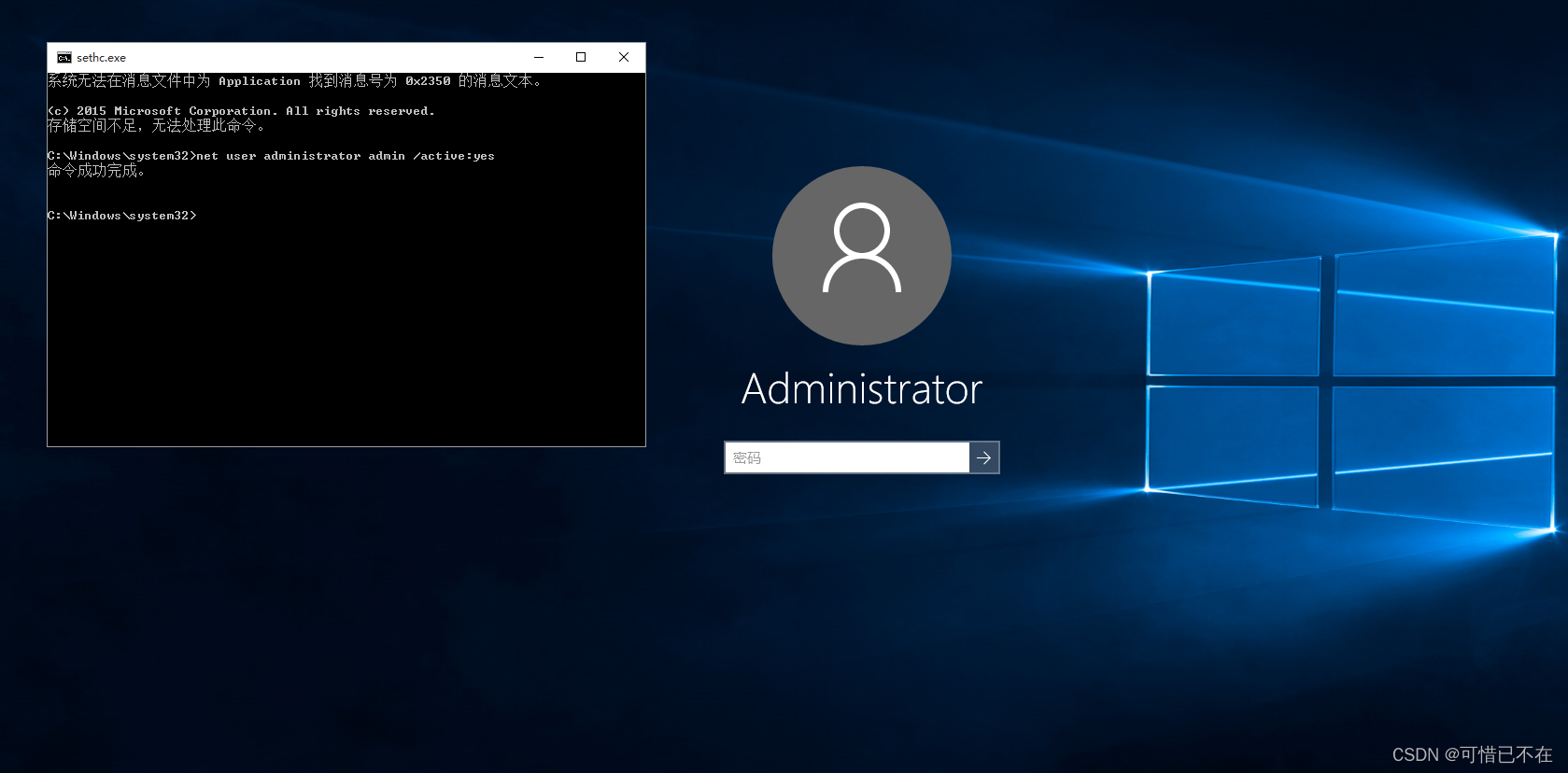
利用Windows10漏洞破解密码(保姆级教学)
前言: 本篇博客只是技术分享并非非法传播知识,实验内容均是在虚拟机中进行,并非真实环境 正文: 一.windows10电脑密码破解 1)开启windows10虚拟机,停留在这个页面 2)按5次Shift键,出现这个粘滞键,如果没有出现的,则说明漏洞已经修复 3)重新启动,在这个页面的时候…...

apk反编译修改教程系列---简单修改apk默认横竖屏显示 手机端与电脑端同步演示【十一】
往期教程: apk反编译修改教程系列-----修改apk应用名称 任意修改名称 签名【一】 apk反编译修改教程系列-----任意修改apk版本号 版本名 防止自动更新【二】 apk反编译修改教程系列-----修改apk中的图片 任意更换apk桌面图片【三】 apk反编译修改教程系列---简单…...

2301: 不定方程解的个数
题目描述 输出不定方程解的个数。在数学中,不定方程是数论中的一个重要课题,在各种比赛中也常常出现. 对于不定方程,有时我们往往只求非负整数解,现有方程axbyc0,其中x、y为未知量且不超过10000,当给定a、…...

vue3学习——封装菜单栏
/Layout/Sidebar/index.vue <script setup lang"ts"> import Sidebar from ./Sidebar.vue // 在下面的代码里 import { useRoute } from vue-router import useUserStore from /store/modules/user.ts // state中存放菜单数据 import useLayoutSetting from /…...

深度学习的进展及其在各领域的应用
深度学习,作为人工智能的核心分支,近年来在全球范围内引起了广泛的关注和研究。它通过模拟人脑的学习机制,构建复杂的神经网络结构,从大量数据中学习并提取有用的特征表示,进而解决各种复杂的模式识别问题。 一、深度…...
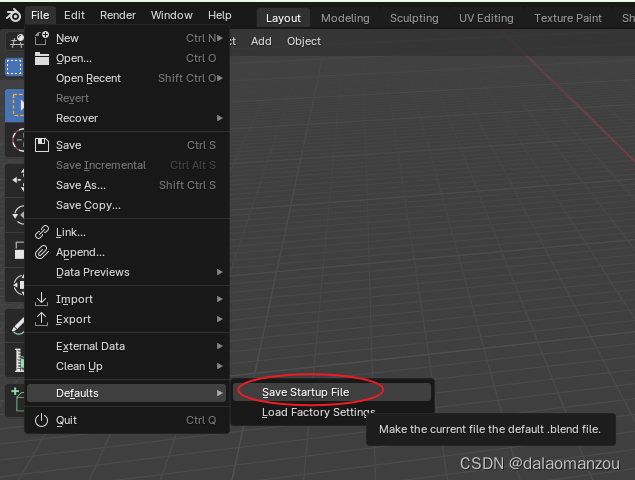
blender怎么保存窗口布局,怎么设置默认输出文件夹
进行窗口布局大家都会,按照自己喜好来就行了,设置输出文件夹如图 这些其实都简单。关键问题在于,自己调好了窗口布局,或者设置好了输出文件夹之后,怎么能让blender下次启动的时候呈现出自己设置好的窗口布局ÿ…...

【开源】基于JAVA+Vue+SpringBoot的实验室耗材管理系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 耗材档案模块2.2 耗材入库模块2.3 耗材出库模块2.4 耗材申请模块2.5 耗材审核模块 三、系统展示四、核心代码4.1 查询耗材品类4.2 查询资产出库清单4.3 资产出库4.4 查询入库单4.5 资产入库 五、免责说明 一、摘要 1.1…...
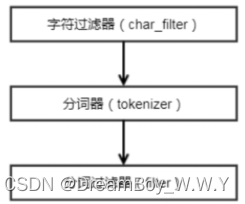
【ES】--Elasticsearch的分词器详解
目录 一、前言二、分词器原理1、常用分词器2、ik分词器模式3、指定索引的某个字段进行分词测试3.1、采用ts_match_analyzer进行分词3.2、采用standard_analyzer进行分词三、如何调整分词器1、已存在的索引调整分词器2、特别的词语不能被拆开一、前言 最近项目需求,针对客户提…...

【算法】{画决策树 + dfs + 递归 + 回溯 + 剪枝} 解决排列、子集问题(C++)
文章目录 1. 前言2. 算法例题 理解思路、代码46.全排列78.子集 3. 算法题练习1863.找出所有子集的异或总和再求和47.全排列II17.电话号码的字母组合 1. 前言 dfs问题 我们已经学过,对于排列、子集类的问题,一般可以想到暴力枚举,但此类问题用…...

sqlserver 存储过程
在 SQL Server 中,存储过程(Stored Procedure)是一种预编译的 SQL 代码块,可以接受参数,执行一系列 SQL 语句,并返回一个或多个结果集。存储过程可以看作是一种封装了 SQL 语句的函数,可以在需要…...

C语言什么是悬空指针?
一、问题 什么是悬空指针?为什么会出现?我们该如何避免悬空指针的出现? 二、解答 在C语言中,悬空指针指的是指向已删除(或释放)的内存位置的指针。如果一个指针指向的内存被释放,但指针本身并未…...

AES加密后的密码可以破解吗
AES(高级加密标准)是一种广泛使用的对称加密算法,设计用来抵御各种已知的攻击方法。AES使用固定块大小的加密块和密钥长度,通常是128、192或256位。它被认为是非常安全的,到目前为止,没有已知的可行方法能够…...

vue3学习——路由进度条
安装 pnpm i nprogress创建permission.ts import router from /router/index.ts import NProgress from nprogress import nprogress/nprogress.css // 不加样式不显示 NProgress.configure({ showSpinner: false }) router.beforeEach((to, from, next) > {console.log(t…...

VMware虚拟机安装Windows系统教程
前言 今天给小伙伴分享一个安装Windows系统的教程,本教程适用于WindowsXP/7/8/8.1/10。 安装的系统前需要先检查一下你的电脑硬件环境,每个系统的硬件要求都不一样哦~ 硬件要求指的是你的电脑主机的配置,如果低于这个配置的&am…...

vue3学习——router-view 过渡动画
虽然vue3说建vue页面不用包裹一个根节点,但是transition不能没有唯一的标签 所以还是得包一层~ o( ̄▽ ̄)o <el-main><router-view v-slot"{ Component, route }"><transition name"MainFade" mode"o…...
从HSE攻击事件漫谈针对勒索攻击防御的两大误区
前言 HSE遭到严重的勒索软件攻击,爱尔兰的医疗服务系统是该国的公共资助医疗系统,在受到勒索病毒攻击之后,被迫在上周五关闭其 IT 系统,以此作为预防措施,避免威胁扩散。该事件导致该国家多家医院的服务取消和中断&am…...
外观模式)
设计模式(结构型模式)外观模式
目录 一、简介二、外观模式2.1、子系统2.2、外观类2.3、使用 三、优点与缺点 一、简介 外观模式(Facade Pattern)是一种结构型设计模式,提供了一个统一的接口,用于访问子系统中的一组接口。这个模式隐藏了子系统的复杂性ÿ…...

C语言函数的栈帧与销毁(面试亮点)
目录 如果你能熟练的掌握函数的栈帧与销毁在面试中是及其亮眼的加分项,所以我们来以实例来将解函数是如何实现栈帧与销毁的。 一. 函数栈帧 二.寄存器 三. 用例题讲解创建栈帧的过程 3.1 main 函数的反汇编代码。 第一步:给调用main函数的函数分配…...
实现 字符串动画)
使用 GreenSock(GSAP)实现 字符串动画
要使用 GreenSock(GSAP)实现 "JianMa XinXi" 这个字符串的动画,其中两个 x 字符自动旋转,j 和 m 字符上下跳动,并且美化这个字符串使其可以作为 logo 使用,我们可以通过以下步骤来实现࿱…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...
