矩阵在计算机图像处理中的应用
矩阵在计算机图像处理中是非常核心的概念,因为它们为表示和操作图像数据提供了一种非常方便和强大的方式。以下是矩阵在计算机图像处理中的一些关键作用:
-
图像表示:在计算机中,图像通常被表示为像素矩阵,也就是二维数组。在灰度图像中,数组的每个元素对应于图像中的一个像素,数值表示该像素的光强,即亮度。对于彩色图像,通常使用三个矩阵来表示红色、绿色、蓝色三个颜色通道。所以,本质上,图像可以看作是一个或多个矩阵。
-
像素操作:图像处理经常需要对像素值进行调整,比如调整亮度、对比度或应用各种滤波效果。这些操作往往涉及对整个像素矩阵执行算术运算,如加法、减法、乘法和除法。
-
几何变换:要在图像上执行诸如旋转、缩放、倾斜或其他几何变换,通常会用到变换矩阵。使用适当的变换矩阵,可以通过线性代数中的矩阵乘法来计算图像点变换后的新位置,这些操作是图像处理中的重要基础。
-
滤波和卷积:图像处理中使用的很多滤波器都是通过矩阵(称为卷积核或滤波器核)来定义的。应用滤波器涉及在原始像素矩阵上进行卷积运算,这通常意味着将卷积核矩阵在图像上移动,并对重叠区域的像素值进行加权求和。
-
特征提取:在图像识别或分类中,提取图像的特征是很重要的一步。这些特征通常以矩阵的形式表示,编码了图像的关键信息。这些特征可以来自图像的原始像素,也可以是经过各种变换(例如,傅立叶变换、小波变换)得到的矩阵。
-
图像压缩:图像压缩算法,比如JPEG,会利用变换(如离散余弦变换DCT)将图像数据从像素域转换成频率域,并在该域进行处理。这些变换通常用矩阵形式来表示和实现。
在所有这些情况下,矩阵运算都是进行有效和高效图像处理的基础。因为矩阵是数学中定义明确、性质良好的结构,所以矩阵算法可以高效地实现在硬件和图形处理单元(GPU)上。这使得即便是对于高分辨率的图像,处理操作也可以在可接受的时间内完成。
相关文章:

矩阵在计算机图像处理中的应用
矩阵在计算机图像处理中是非常核心的概念,因为它们为表示和操作图像数据提供了一种非常方便和强大的方式。以下是矩阵在计算机图像处理中的一些关键作用: 图像表示:在计算机中,图像通常被表示为像素矩阵,也就是二维数组…...

Java实现教学资源共享平台 JAVA+Vue+SpringBoot+MySQL
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 数据中心模块2.2 课程档案模块2.3 课程资源模块2.4 课程作业模块2.5 课程评价模块 三、系统设计3.1 用例设计3.2 类图设计3.3 数据库设计3.3.1 课程档案表3.3.2 课程资源表3.3.3 课程作业表3.3.4 课程评价表 四、系统展…...
:使用 ant.jar 执行 SQL 脚本文件)
Spring Boot(六十五):使用 ant.jar 执行 SQL 脚本文件
ant用处,主要用在编译java文件,打包,部署。打包:jar,war,ear包等。ant在项目中有很重要的作用。今天我们讲解它的另一个作用:执行 SQL 脚本文件。 1 引入依赖 <dependency><groupId>org.apache.ant</groupId><artifactId>ant</artifactId&g…...
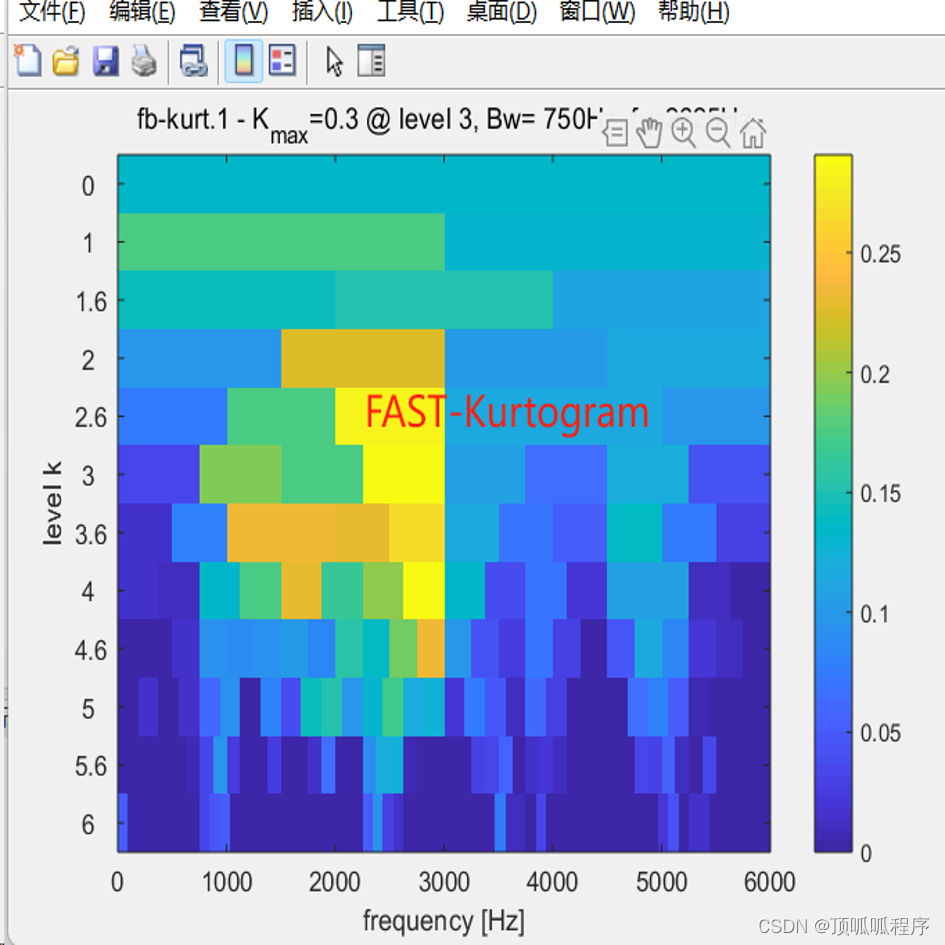
161基于matlab的快速谱峭度方法
基于matlab的快速谱峭度方法,选择信号峭度最大的频段进行滤波,对滤波好信号进行包络谱分析。输出快速谱峭度及包络谱结果。程序已调通,可直接运行。 161 信号处理 快速谱峭度 包络谱分析 (xiaohongshu.com)...
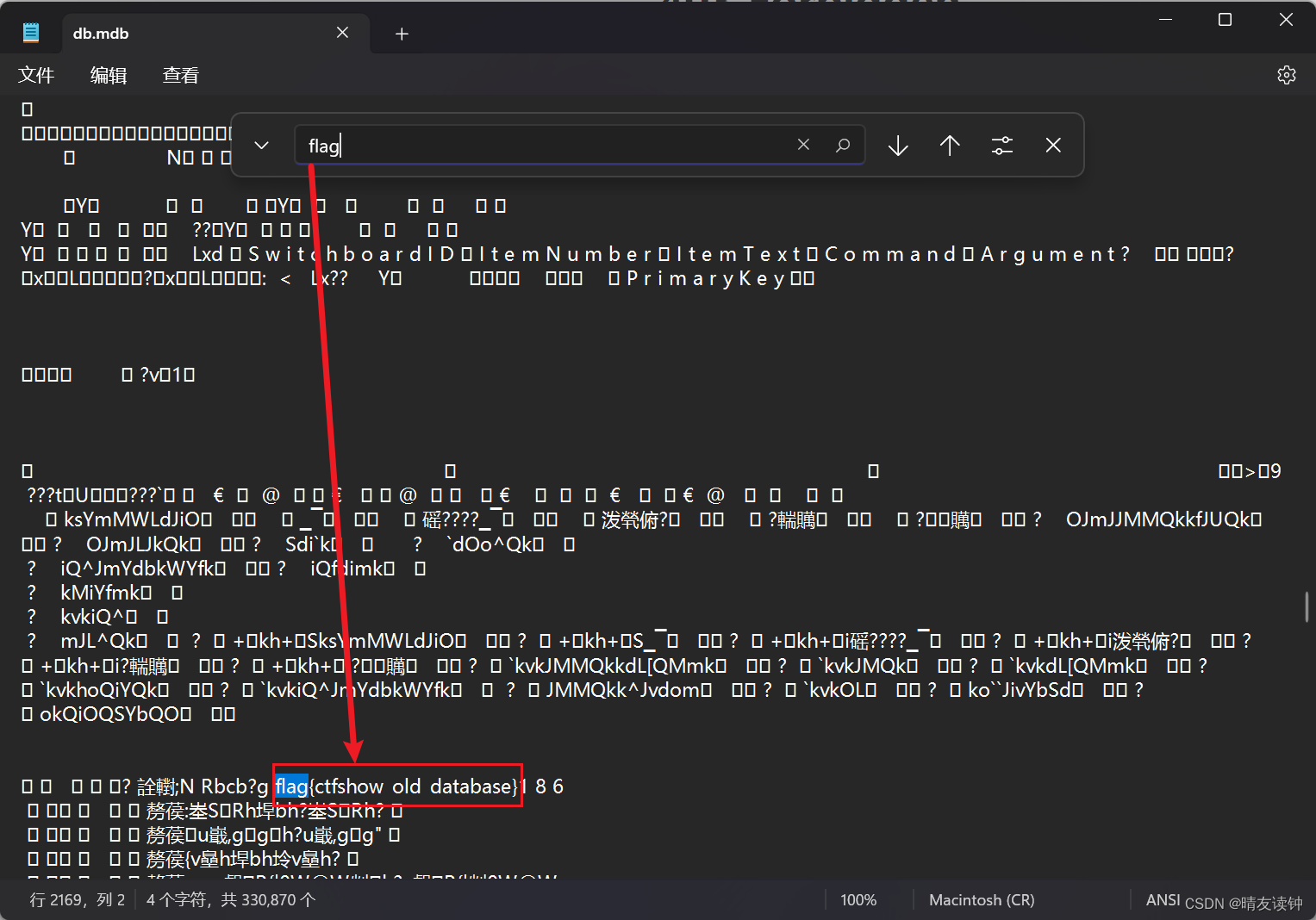
CTFshow-WEB入门-信息搜集
web1(查看注释1) wp 右键查看源代码即可找到flag web2(查看注释2) wp 【CtrlU】快捷键查看源代码即可找到flag web3(抓包与重发包) wp 抓包后重新发包,在响应包中找到flag web4(robo…...
)
django密码管理器(创建项目)
目录 创建项目 安装django 创建项目(django-admin) 创建管理员用户 创建数据库 创建项目 新建一个项目文件夹,如"密码管理器" 安装django 要先安装pip,pip安装地址:pypi.org、pypi.python.org、cheeseshop.python.org pip install django 创建项…...

Centos7之Oracle12c安装与远程连接配置
Centos7之Oracle12c安装与远程连接配置 文章目录 Centos7之Oracle12c安装与远程连接配置1.Oracle官网2. Centos7中安装Oracle12c(12.2.0.1.0)2.1 Introduction (介绍)2.2 Prerequisites(先决条件)2.3 Installation Steps(安装步骤)2.4 Oracle Installer Screens(Oracle安装程序…...
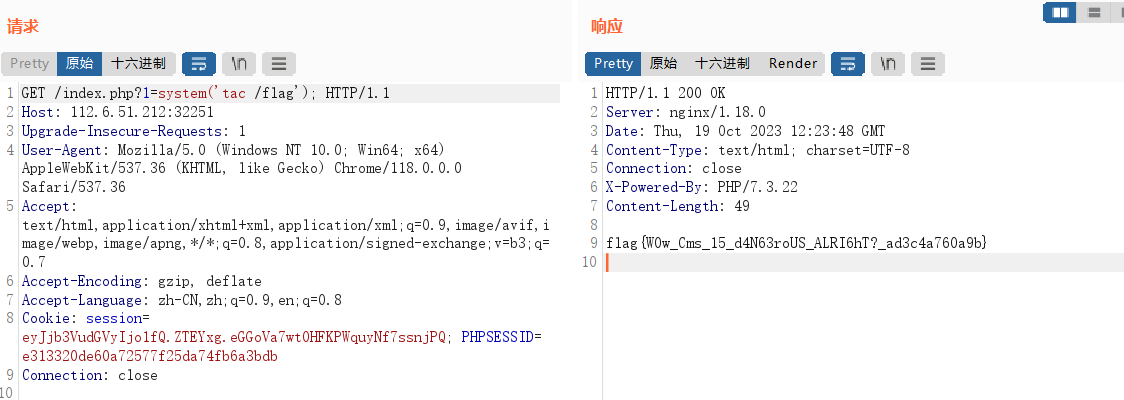
CVE-2022-25578 漏洞复现
CVE-2022-25578 路由/admin/admin.php是后台,登录账号和密码默认是admin、tao,选择文件管理。 是否还记得文件上传中的.htaccess配置文件绕过发,在这个文件中加入一句AddType application/x-httpd-php .jpg,将所有jpg文件当作php…...
)
Ubuntu22.04安装黑屏(进入U盘安装引导时 和 安装完成后)
一:进入U盘安转引导时黑屏 问题描述:选择’try or install ubuntu’,开始安装,出现黑屏。 解决方法:(可行) 安装时,先选择" try or install ubuntu", 此时不要按enter&a…...
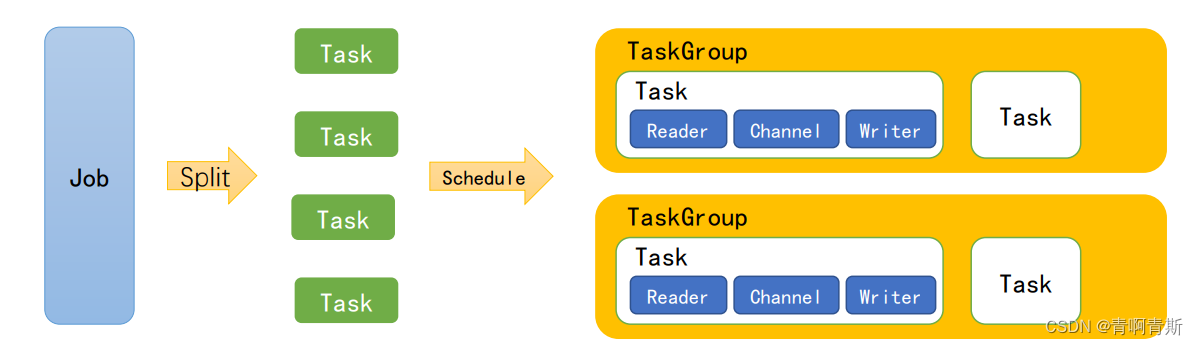
一、DataX简介
DataX简介 一、什么是DataX二、DataX设计三、支持的数据源四、框架设计五、运行原理六、DataX和Sqoop对比 一、什么是DataX DataX是阿里巴巴开源的一个异构数据源离线同步工具,致力于实现包括关系型数据库(MySQL、Oracle等)、HDFS、Hive、OD…...

直播app开发,技术驱动的实时互动新纪元
随着互联网技术的快速发展,直播已成为我们日常生活的重要组成部分。从娱乐、教育到商业活动,直播的广泛应用正在改变着我们的生活和工作方式。在这一变革中,直播开发扮演着至关重要的角色。本文将探讨直播开发的核心理念、技术挑战以及未来的…...

Apache POI的介绍以及使用示例
Apache POI 是一套开源的 Java 库,用于读取和写入 Microsoft Office 文档格式,如 Excel、Word 和 PowerPoint。Spring Boot 是一个流行的 Java 应用程序框架,用于简化 Spring 应用的开发和部署。将 Apache POI 与 Spring Boot 结合使用&#…...

npm config set registry https://registry.npm.taobao.org 这个设置了默认的镜像源之后如何恢复默认的镜像源
要恢复npm默认的镜像源,你可以使用以下命令将registry设置回npm的官方源: npm config set registry https://registry.npmjs.org/这个命令会修改你的全局npm配置,将包的下载源改回npm官方的源。这样做之后,任何后续的npm install…...

算法沉淀——位运算(leetcode真题剖析)
算法沉淀——位运算 常用位运算总结1.基础位运算2.确定一个数中第x位是0还是13.将一个数的第x位改成14.将一个数的第x位改成05.位图6.提取一个数最右边的17.删掉一个数最右边的18.异或运算9.基础例题 力扣题目讲解01.面试题 01.01. 判定字符是否唯一02.丢失的数字03.两整数之和…...
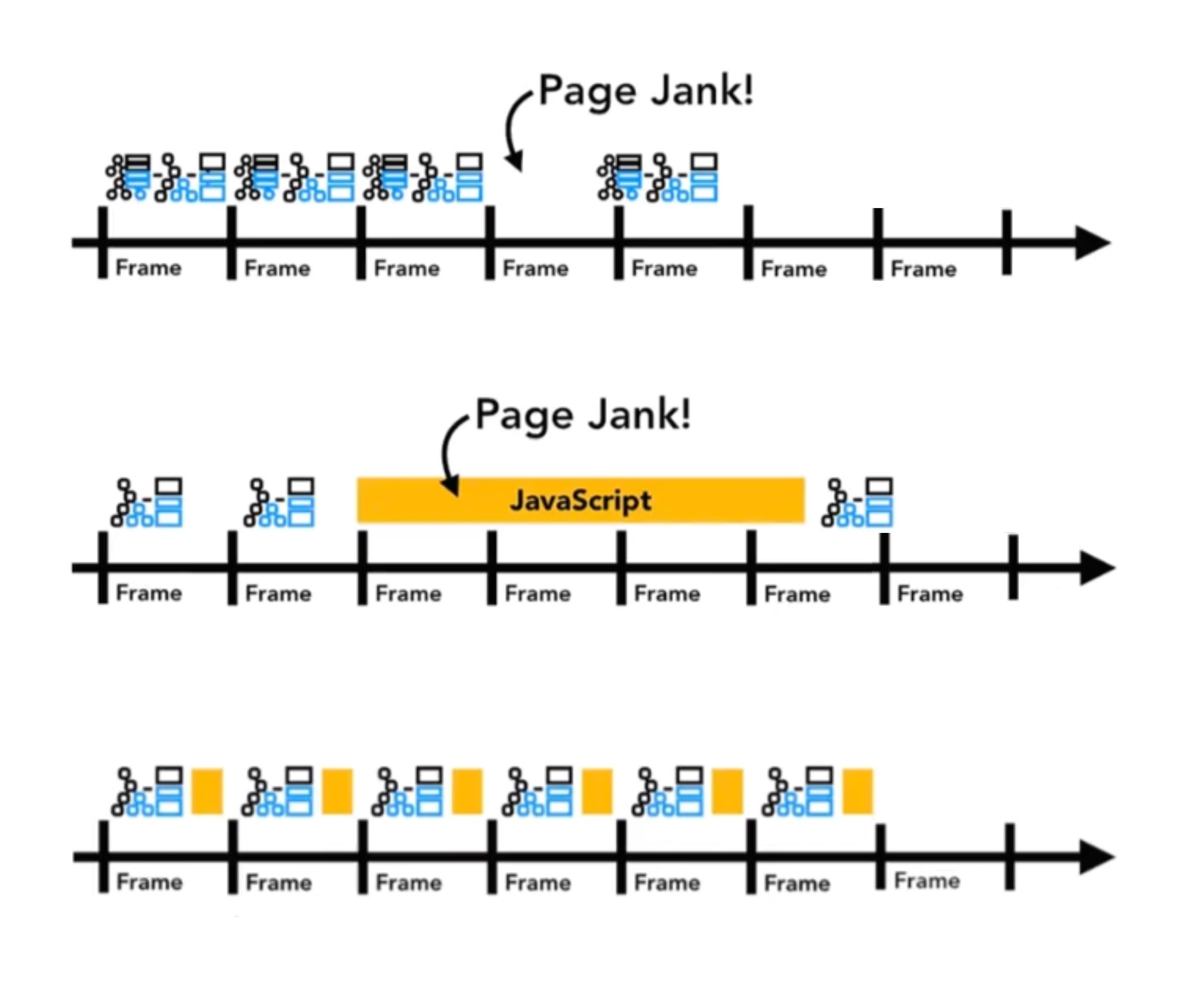
React18原理: 再聊Fiber架构下的时间分片
时间分片 react的任务可以被打断,其实就是基于时间分片的人眼最高能识别的帧数不超过30帧,电影的帧数差不多是在24浏览器的帧率一般来说是60帧,也就是每秒60个画面, 平均一个画面大概是16.5毫秒左右浏览器正常的工作流程是运算渲染ÿ…...

【玩转408数据结构】线性表——线性表的顺序表示(顺序表)
知识回顾 通过前文,我们了解到线性表是具有相同数据类型的有限个数据元素序列;并且,线性表只是一种逻辑结构,其不同存储形式所展现出的也略有不同,那么今天我们来了解一下线性表的顺序存储——顺序表。 顺序表的定义 …...

图像处理之《黑盒扰动的可逆噪声流鲁棒水印》论文阅读
一、文章摘要 近年来,基于深度学习的数字水印框架得到了广泛的研究。现有的方法大多采用基于“编码器-噪声层-解码器”的架构,其中嵌入和提取过程分别由编码器和解码器完成。然而,这种框架的一个潜在缺点是编码器和解码器可能不能很好地耦合…...

一个Vivado仿真问题的debug
我最近在看Synopsys的MPHY仿真代码,想以此为参考写个能实现PWM-G1功能的MPHY,并应用于ProFPGA原型验证平台。我从中抽取了一部分代码,用Vivado自带的仿真器进行仿真,然后就遇到了一个莫名其妙的问题,谨以此文作为debug…...

C#阿里云消息列队推送消息
推送消息到队列 IMNS nativeclient new Aliyun.MNS.MNSClient(accessKeyId, accessKeySecret, endpoint, _stsToken);var nativeSend nativeclient.GetNativeTopic("SMQ");nativeSend.PublishMessage("推送消息内容"); 需要引用Aliyun.MNS.dll 下载地址…...
Stable Diffusion 模型下载:majicMIX sombre 麦橘唯美
本文收录于《AI绘画从入门到精通》专栏,专栏总目录:点这里。 文章目录 模型介绍生成案例案例一案例二案例三案例四案例五案例六案例七案例八案例九案例十...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...
