springmvc中的数据提交方式
一、单个数据提交数据
jsp代码:
<h2>1单个数据提交</h2>
<form action="${pageContext.request.contextPath}/one.action">name<input name="myname"/><br>age<input name="age"><input type="submit" value="提交">
</form>测试代码:
@Controller
public class DataSubmitAction {@RequestMapping("/one.action")public String one(String myname, int age) {System.out.println("myname=" + myname + ",age=" + (age + 10));return "main";}二、对象封装提交数据
【注】需要保证请求参数的名称与实体类中成员变量名称一致
jsp代码:
<h2>2对象数据封装数据提交</h2>
<form action="${pageContext.request.contextPath}/two.action">name<input name="name"/><br>age<input name="age"><br><input type="submit" value="提交">
</form>测试代码:
@RequestMapping("/two.action")public String two(User user) {System.out.println(user);return "main";}三、动态占位符提交数据
【注】只能用于超链接或地址提交数据,使用注解来解析
jsp代码:
<h2>3.动态占位符提交</h2>
<a href="${pageContext.request.contextPath}/three/张三/20.avction">动态提交</a>测试代码:
@RequestMapping("/three/{name}/{age}.action")public String three(@PathVariable String name, @PathVariable int age) {System.out.println("myname=" + name + ",age=" + (age + 10));return "main";}四、映射名称不一致的时候如何提交数据
【注】提交请求参数与action方法的形参的名称不一致,使用注解@RequestParam来解析
jsp代码:
<h2>4.参数名称不一致解决方案</h2>
<form action="${pageContext.request.contextPath}/four.action" method="post">name<input name="name"/><br>age<input name="age"><br><input type="submit" value="提交">
</form>测试代码:
@RequestMapping("/four.action")public String four(@RequestParam("name") String n, @RequestParam("age") int a) {System.out.println("myname=" + n + ",age=" + (a + 10));return "main";}五、手工提取数据
jsp代码:
<h2>5手工提取数据</h2>
<form action="${pageContext.request.contextPath}/five.action">name<input name="name"/><br>age<input name="age"><input type="submit" value="提交">
</form>测试代码:
@RequestMapping("/five.action")public String five(HttpServletRequest request) {String name = request.getParameter("name");int age = Integer.parseInt(request.getParameter("age"));System.out.println("myname=" + name + ",age=" + (age + 10));return "main";}
相关文章:

springmvc中的数据提交方式
一、单个数据提交数据 jsp代码: <h2>1单个数据提交</h2> <form action"${pageContext.request.contextPath}/one.action">name<input name"myname"/><br>age<input name"age"><input type&…...

unity2017 遇到visual studio 2017(社区版) 30日试用期到了
安装unity2017 遇到visual studio 2017 30日试用期到了,网上百度搜了好多方法都没有成功。 最后用了这个方法: 1)启动vs2017,在弹出要登录的窗口之前,迅速的点击工具-》选项-》账户,勾选在添加账户或对账户重新进行身…...
Netty应用(六) 之 异步 Channel
目录 12.Netty异步的相关概念 12.1 异步编程的概念 12.2 方式1:主线程阻塞,等待异步线程完成调用,然后主线程发起请求IO 12.3 方式2:主线程注册异步线程,异步线程去回调发起请求IO 12.4 细节注释 12.5 异步的好处…...
STM32CubeMx+MATLAB Simulink串口输出实验,UART/USART串口测试实验
STM32CubeMxMATLAB Simulink串口输出实验...
【51单片机】串口通信实验(包括波特率如何计算)
目录 串口通信实验通信的基本概念串行通信与并行通信异步通信与同步通信单工、 半双工与全双工通信通信速率 51单片机串口介绍串口介绍串口通信简介串口相关寄存器串口工作方式方式0方式1方式 2 和方式 3 串口的使用方法(计算波特率) 硬件设计软件设计1、…...
Kafka零拷贝技术与传统数据复制次数比较
读Kafka技术书遇到困惑: "对比传统的数据复制和“零拷贝技术”这两种方案。假设有10个消费者,传统复制方式的数据复制次数是41040次,而“零拷贝技术”只需110 11次(一次表示从磁盘复制到页面缓存,另外10次表示10个消费者各自…...

npm ERR! network This is a problem related to network connectivity.
遇到 ETIMEDOUT 错误时,这表明npm尝试连接到npm仓库时超时了,这通常是由网络连接问题引起的。这可能是因为网络不稳定、连接速度慢、或者你的网络配置阻止了对npm仓库的访问。以下是一些解决这个问题的步骤: 1. 检查网络连接 首先ÿ…...

【SQL高频基础题】619.只出现一次的最大数字
题目: MyNumbers 表: ------------------- | Column Name | Type | ------------------- | num | int | ------------------- 该表可能包含重复项(换句话说,在SQL中,该表没有主键)。 这张表的每…...
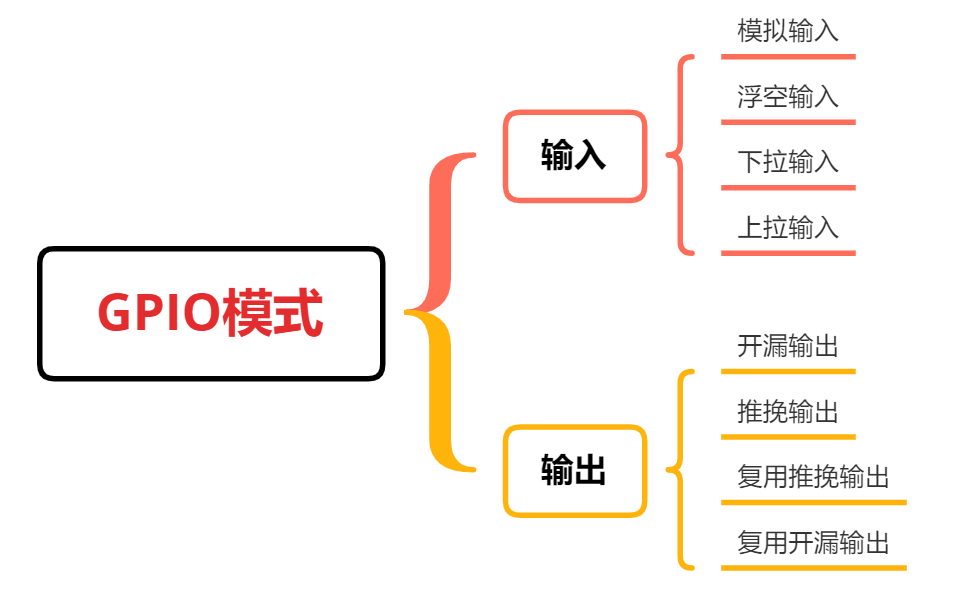
STM32F1 - GPIO外设
GPIO 1> 硬件框图2> 工作模式 1> 硬件框图 2> 工作模式 C语言描述 /** * brief Configuration Mode enumeration */typedef enum { GPIO_Mode_AIN 0x0, // Analog Input 模拟输入 GPIO_Mode_IN_FLOATING 0x04, // input floating 浮空输入GPIO_Mode_I…...

新增同步管理、操作日志模块,支持公共链接分享,DataEase开源数据可视化分析平台v2.3.0发布
2024年2月5日,DataEase开源数据可视化分析平台正式发布v2.3.0版本。 这一版本的功能升级包括:新增“同步管理”功能模块,用户可通过此模块,将传统数据库中的数据定时同步到Apache Doris中,让数据分析更快速࿱…...

跟着pink老师前端入门教程-day19
一、移动WEB开发之流式布局 1、 移动端基础 1.1 浏览器现状 PC端常见浏览器:360浏览器、谷歌浏览器、火狐浏览器、QQ浏览器、百度浏览器、搜狗浏览器、IE浏览器。 移动端常见浏览器:UC浏览器,QQ浏览器,欧朋浏览器࿰…...

ChatGPT学习第一周
📖 学习目标 掌握ChatGPT基础知识 理解ChatGPT的基本功能和工作原理。认识到ChatGPT在日常生活和业务中的潜在应用。 了解AI和机器学习的基本概念 获取人工智能(AI)和机器学习(ML)的初步了解。理解这些技术是如何支撑…...
爬爬爬——今天是浏览器窗口切换和给所选人打钩(自动化)
学习爬虫路还很长,第一阶段花了好多天了,还在底层,虽然不是我专业要学习的语言,和必备的知识,但是我感觉还挺有意思的。加油,这两天把建模和ai也不学了,唉过年了懒了! 加油坚持就是…...
Netty应用(五) 之 Netty引入 EventLoop
目录 第三章 Netty 1.什么是Netty? 2.为什么需要使用Netty? 3.Netty的发展历程 4.谁在使用Netty? 5.为什么上述这些分布式产品都使用Netty? 6.第一个Netty应用 7.如何理解Netty是NIO的封装 8.logback日志使用的加强 9.Ev…...
【c++基础】国王的魔镜
说明 国王有一个魔镜,可以把任何接触镜面的东西变成原来的两倍——只是,因为是镜子嘛,增加的那部分是反的。 比如一条项链,我们用AB来表示,不同的字母表示不同颜色的珍珠。如果把B端接触镜面的话,魔镜会把…...
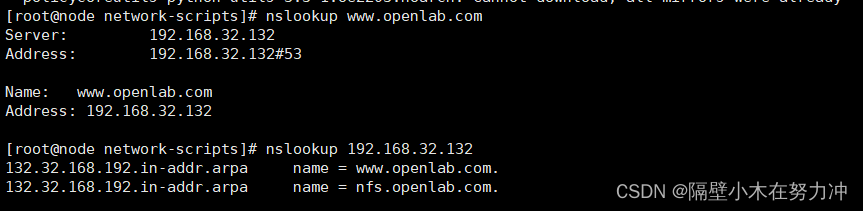
配置DNS正反向解析服务!!!!
一.准备工作 #关闭防火墙和selinux,或者允许服务通过 [rootnode ~]# nmcli c mod ens32 ipv4.method manual ipv4.address 192.168.32.133/24 ipv4.gateway 192.168.32.2 ipv4.dns 192.168.32.132 [rootnode ~]# nmcli c reload [rootnode ~]# nmcli c up ens32[rootnode ~]# …...

大模型2024规模化场景涌现,加速云计算走出第二增长曲线
导读:2024,大模型第一批规模化应用场景已出现。 如果说“百模大战”是2023年国内AI产业的关键词,那么2024年我们将正式迈进“应用为王”的新阶段。 不少业内观点认为,2024年“百模大战”将逐渐收敛甚至洗牌,而大模型在…...
)
Gitlab和Jenkins集成 实现CI (三)
Gitlab和Jenkins集成 实现CI (一) Gitlab和Jenkins集成 实现CI (二) Gitlab和Jenkins集成 实现CI (三) 自动部署 配置免密ssh 进入http服务器 生成ssh密钥 ssh-keygen -t rsa进入jenkins(容器) 拷贝公钥 ssh-copy-id http服务器用户名http服务器ip #输入http服务器密码配…...

随机过程及应用学习笔记(二)随机过程的基本概念
随机过程论就是研究随时间变化的动态系统中随机现象的统计规律的一门数学学科。 目录 前言 一、随机过程的定义及分类 1、定义 2、分类 二、随机过程的分布及其数字特征 1、分布函数 2、数字特征 均值函数和方差函数 协方差函数和相关函数 3、互协方差函数与互相关函…...

【机器学习】Kmeans如何选择k值
确定 K 值是 K-means 聚类分析的一个重要步骤。不同的 K 值可能会产生不同的聚类结果,因此选择合适的 K 值非常重要。 以下是一些常见的方法来选择 K 值: 手肘法:该方法基于绘制聚类内误差平方和(SSE)与 K 值之间的关系图。随着 K 值的增加,SSE会逐渐降低,但降低幅度逐…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...
