CSP-动态规划-最长公共子序列(LCS)
一、动态规划
动态规划(Dynamic Programming,简称DP)主要用于求解可以被分解为相似子问题的复杂问题,特别是在优化问题上表现出色,如最短路径、最大子数组和、编辑距离等。动态规划的核心思想是将原问题分解为较小的子问题,通过解决这些子问题,并将结果存储起来(通常是在一个数组或者哈希表中),以避免重复计算,从而提高效率。
动态规划问题的解决通常遵循以下几个步骤:
- 暴力穷举所有答案。
- 画出递归树,尝试编写递归函数求解。
- 若遍历中存在大量重复计算,使用哈希表缓存数据,之后遍历到相同节点就直接查表。
- 表示整个计算过程,观察公式求解顺序,改写成更加高效的迭代形式。
二、动态规划的例子
1.斐波那契数列
2.背包问题
3. 最长公共子序列(LCS)
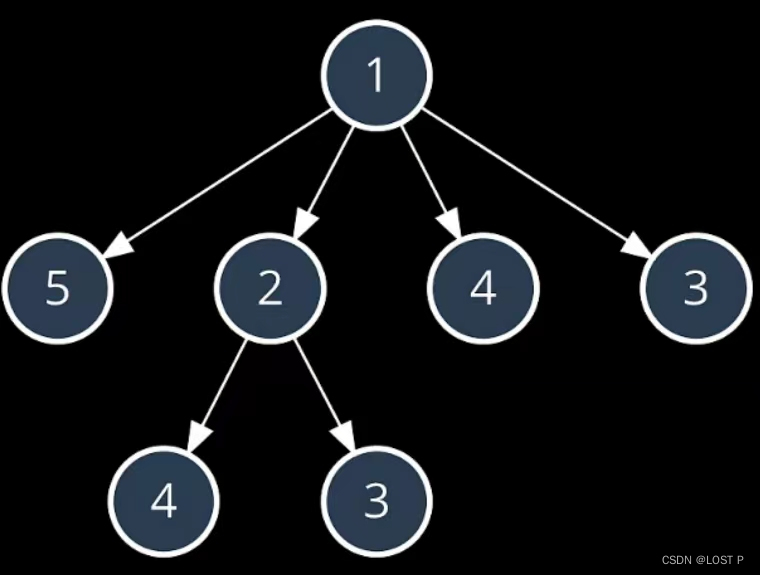
- 给定一个无序数组
nums=[1,5,2,4,3],找出其中最长的递增的子序列,比如1-2-4,1-2-3。将问题简化,要求算法只返回最长序列的长度(3)
(1) 暴力枚举
- 把每个子序列都“找个遍”,并且在遍历过程中实时记录当前子序列的长度
(2) 递归解决方案
-
递归函数
L:用于计算以特定元素结尾的最长递增子序列的长度;- 基础情形:如果当前考虑的元素是数组的最后一个元素,那么以它结尾的最长递增子序列的长度为 1,因为它自身就构成了一个长度为 1 的递增子序列。
- 递归步骤:对于非最后一个元素,函数会遍历当前元素之后的所有元素,寻找一个值比当前元素大的元素,这意味着可以形成一个递增的序列。对于每一个这样的元素,函数会递归地计算以那个元素为结尾的最长递增子序列的长度,并将其与当前最大长度比较,更新当前最大长度。这个过程会重复直到数组结束。
- 返回值:函数最终返回以当前元素结尾的最长递增子序列的长度。
-
函数
lengthOfLIS:作用是找到整个数组的最长递增子序列的长度。- 遍历给定数组的每个元素,对每个元素调用递归函数
L,计算以该元素为结尾的最长递增子序列的长度。 - 比较并更新
max_len为当前找到的最长递增子序列的长度。 - 遍历完成后,返回
max_len作为最终结果。
- 遍历给定数组的每个元素,对每个元素调用递归函数
#include <iostream>
#include <vector>
using namespace std;// 计算以 nums[i] 结尾的最长递增子序列的长度
int L(const vector<int>& nums, int i) {if (i == nums.size() - 1) { // 如果是最后一个元素return 1; // 最长递增子序列长度为1}int max_len = 1; // 初始化最大长度为1for (int j = i + 1; j < nums.size(); ++j) {if (nums[j] > nums[i]) { // 如果找到一个递增的元素// 递归计算以 nums[j] 结尾的最长递增子序列长度,并加1(加上nums[i])// 然后与当前的最大长度取较大值max_len = max(max_len, L(nums, j) + 1);}}return max_len; // 返回以 nums[i] 结尾的最长递增子序列的长度
}// 计算给定序列的最长递增子序列长度
int lengthOfLIS(const vector<int>& nums) {int max_len = 0; // 初始化全局最大长度为0for (int i = 0; i < nums.size(); ++i) {// 遍历每个元素,计算以每个元素为起点的最长递增子序列的长度// 然后取所有长度中的最大值max_len = max(max_len, L(nums, i));}return max_len; // 返回最长递增子序列的长度
}int main() {vector<int> nums = {1, 5, 2, 4, 3}; cout << lengthOfLIS(nums) << endl; return 0;
}(3) 递归的问题
- 直接递归的方法在时间复杂度上是非常高的,因为它会重复计算很多子问题的解。
- 比如,在遍历子序列1-2-4时就已经计算过“L(4)”,后面遍历1,4时又重复计算了一次。
(4) 递归的优化:动态规划
-
为了避免递归中出现的重复计算,可以将第一次计算时的结果保存,之后再当遍历到相同的节点我们就不在需要重复计算,直接返回之前的结果即可。
-
在这个版本中,
L函数中添加了一个unordered_map(哈希表)类型的备忘录memo,用于存储已经计算过的子问题的解。在递归的过程中,先检查备忘录是否已经包含了当前子问题的解,如果有则直接返回保存的结果,避免了重复计算。这样能够显著提高程序的性能。
#include <iostream>
#include <vector>
#include <unordered_map>
using namespace std;// 使用备忘录的递归方式计算以 nums[i] 结尾的最长递增子序列的长度
int L(const vector<int>& nums, int i, unordered_map<int, int>& memo) {if (i == nums.size() - 1) {return 1;}if (memo.find(i) != memo.end()) {return memo[i]; // 如果已经计算过,直接返回保存的结果}int max_len = 1;for (int j = i + 1; j < nums.size(); ++j) {if (nums[j] > nums[i]) {max_len = max(max_len, L(nums, j, memo) + 1);}}memo[i] = max_len; // 将结果保存到备忘录中return max_len;
}// 计算给定序列的最长递增子序列长度
int lengthOfLIS(const vector<int>& nums) {int max_len = 0;unordered_map<int, int> memo; // 使用unordered_map作为备忘录for (int i = 0; i < nums.size(); ++i) {max_len = max(max_len, L(nums, i, memo));}return max_len;
}int main() {vector<int> nums = {1, 5, 2, 4, 3};cout << lengthOfLIS(nums) << endl;return 0;
}
(5) 递归转非递归
-
从后往前依次计算,即可推算出所有答案(数学归纳)
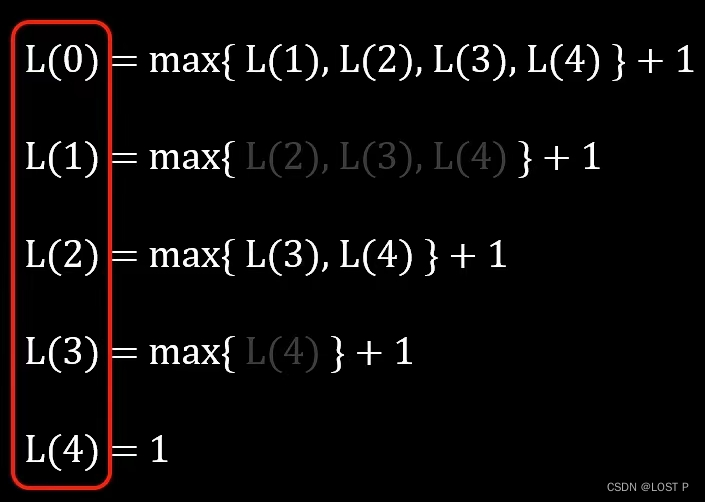
-
dp数组:用于存储以每个元素结尾的最长递增子序列的长度。 -
双重循环:外层循环遍历每个元素,内层循环遍历当前元素之前的元素,更新以当前元素结尾的最长递增子序列的长度。
-
max_element函数:返回 dp 数组中的最大值,即整个数组中最长递增子序列的长度。
#include <iostream>
#include <vector>
using namespace std;int lengthOfLIS(const vector<int>& nums) {int n = nums.size();if (n == 0) return 0; // 处理空数组的情况vector<int> dp(n, 1); // 初始化dp数组,每个元素代表以对应位置元素结尾的最长递增子序列的长度for (int i = 1; i < n; ++i) {for (int j = 0; j < i; ++j) {if (nums[i] > nums[j]) {dp[i] = max(dp[i], dp[j] + 1); // 更新以nums[i]结尾的最长递增子序列长度}}}return *max_element(dp.begin(), dp.end()); // 返回dp数组中的最大值,即最长递增子序列的长度
}int main() {vector<int> nums = {1, 5, 2, 4, 3}; // 定义一个序列cout << lengthOfLIS(nums) << endl; // 输出最长递增子序列的长度return 0;
}
相关文章:
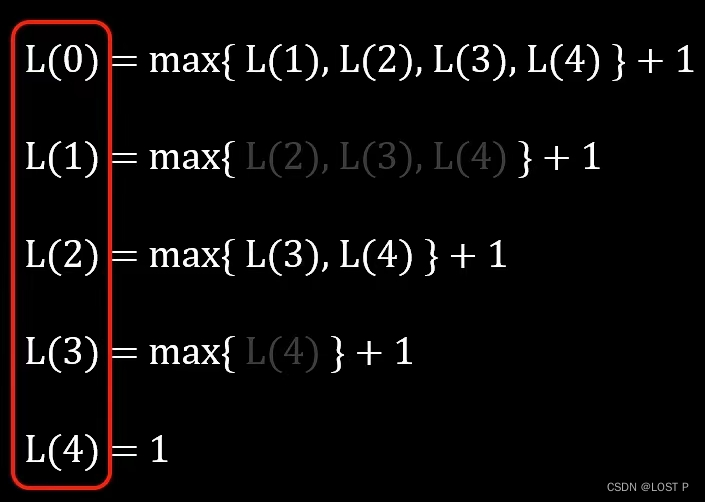
CSP-动态规划-最长公共子序列(LCS)
一、动态规划 动态规划(Dynamic Programming,简称DP)主要用于求解可以被分解为相似子问题的复杂问题,特别是在优化问题上表现出色,如最短路径、最大子数组和、编辑距离等。动态规划的核心思想是将原问题分解为较小的子…...

安装nodejs2011并配置npm仓库
1. 安装nodejs 选择2011版本下载 在安装目录(个人情况)下 D:\Program Files\nodejs2011创建2个文件夹: node_global (依赖库) node_cache (缓存) 然后在当前目录下cmd进入dos窗口,执行: npm c…...
)
排序C++代码(已更:快速排序,归并排序)
一、快速排序 #include<iostream> using namespace std;//设定三个数组,判断排序算法代码的正确性 int a[100]{3,4,2,6,9,7,1,0,1,2,3,3,5,6,7,8,3,4,5}; int b[100]{1,5,3,4}; int c[100]{7,8,9,1,2,3};void quickSort(int* num,int l,int r){if(l>r) re…...

CentOS 7.9安装Tesla M4驱动、CUDA和cuDNN
正文共:1333 字 21 图,预估阅读时间:2 分钟 上次我们在Windows上尝试用Tesla M4配置深度学习环境(TensorFlow识别GPU难道就这么难吗?还是我的GPU有问题?),但是失败了。考虑到Windows…...

Java设计模式——策略
前言 策略模式是平时Java开发中常用的一种,虽然已有很多讲解设计模式的文章,但是这里还是写篇文章来从自己理解的角度讲解一下。 使用场景 我们不妨进行场景假设,要对我们的软件进行授权管理:在启动我们的软件之前先要校验是否…...
线性代数的本质 1 向量
向量是线性代数中最为基础的概念。 何为向量? 从物理上看, 向量就是既有大小又有方向的量,只要这两者一定,就可以在空间中随便移动。 从计算机应用的角度看,向量和列表很接近,可以用来描述某对象的几个不同…...

基于JAVA的贫困地区人口信息管理系统 开源项目
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 人口信息管理模块2.2 精准扶贫管理模块2.3 特殊群体管理模块2.4 案件信息管理模块2.5 物资补助模块 三、系统设计3.1 用例设计3.2 数据库设计3.2.1 人口表3.2.2 扶贫表3.2.3 特殊群体表3.2.4 案件表3.2.5 物资补助表 四…...
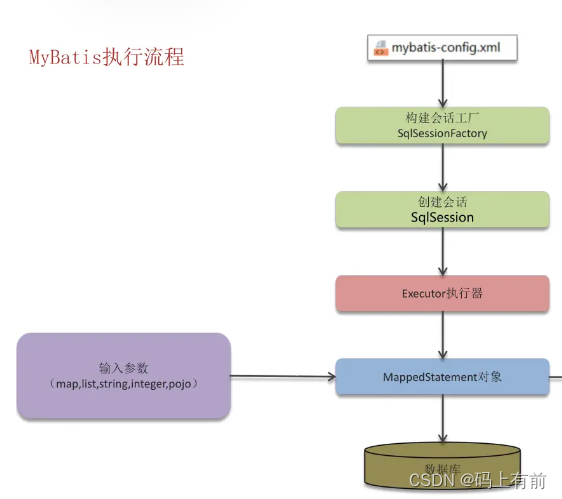
【后端高频面试题--Mybatis篇】
🚀 作者 :“码上有前” 🚀 文章简介 :后端高频面试题 🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬 后端高频面试题--Mybatis篇 什么是Mybatis?Mybatis的优缺点?Mybatis的特点…...

【笔记】Helm-5 Chart模板指南-12 .helmignore文件
.helmignore文件 .helmignore文件用来指定您不想包含在您的helm chart中的文件。 如果该文件存在,helm package命令会在打包应用时忽略所有在.helmignore文件中匹配的文件。 有助于避免不需要的或敏感文件及目录添加到您的helm chart中。 .helmignore文件支持Uni…...
【MySQL】表的增删改查(基础)
MySQL表的增删改查(基础) 1. CRUD2. 新增(Create)2.1 单行数据全列插入2.2 多行数据 指定列插入 3. 查询(Retrieve)3.1 全列查询3.2 指定列查询3.3 查询字段为表达式3.4 别名3.5 去重:DISTINCT…...
Android矩阵Matrix动画缩放Bitmap移动手指触点到ImageView中心位置,Kotlin
Android矩阵Matrix动画缩放Bitmap移动手指触点到ImageView中心位置,Kotlin 借鉴 Android双指缩放ScaleGestureDetector检测放大因子大图移动到双指中心点ImageView区域中心,Kotlin(2)-CSDN博客 在此基础上实现手指在屏幕上点击后&…...

C语言:表达式求值
引言:在笔试中,有一类的题目,题目给出代码,要求分析得出输出结果。这类题目更加考察我们对于运算顺序和运算类型转换的理解。文章介绍了隐式类型转换和操作符注意点,希望增加读者对于表达式求值的理解。 1.隐式类型转…...
GO 的 Web 开发系列(五)—— 使用 Swagger 生成一份好看的接口文档
经过前面的文章,已经完成了 Web 系统基础功能的搭建,也实现了 API 接口、HTML 模板渲染等功能。接下来要做的就是使用 Swagger 工具,为这些 Api 接口生成一份好看的接口文档。 一、写注释 注释是 Swagger 的灵魂,Swagger 是通过…...
【极数系列】Flink集成KafkaSink 实时输出数据(11)
文章目录 01 引言02 连接器依赖2.1 kafka连接器依赖2.2 base基础依赖 03 使用方法04 序列化器05 指标监控06 项目源码实战6.1 包结构6.2 pom.xml依赖6.3 配置文件6.4 创建sink作业 01 引言 KafkaSink 可将数据流写入一个或多个 Kafka topic 实战源码地址,一键下载可用…...

我为什么选择Xamarin开发ios app安卓app
临岁之寒简书作者,转载 Xamarin是一项跨平台开发技术,之前是收费的,而且据说收费不菲,所以使用的人数比较少,在国内几乎无人问津。后来Xamarin被微软收购,现已免费开放,相信今后国内的使用人群会大幅地增长…...
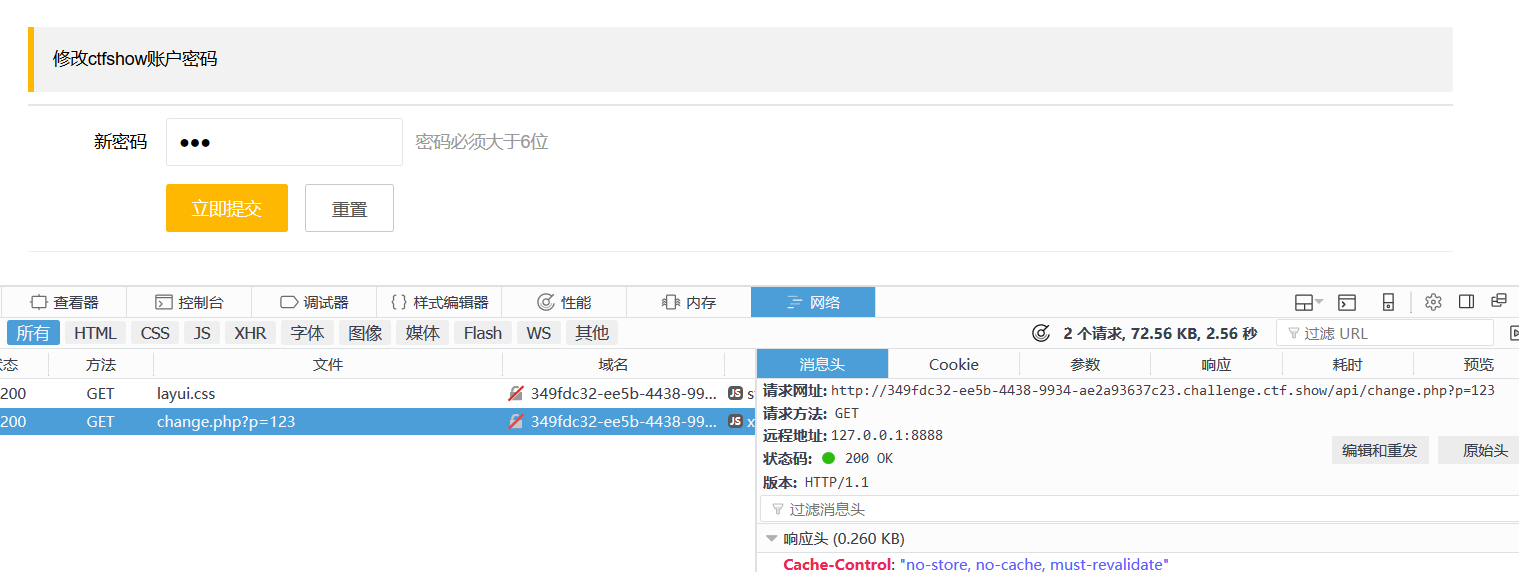
安全基础~通用漏洞4
文章目录 知识补充XSS跨站脚本**原理****攻击类型**XSS-后台植入Cookie&表单劫持XSS-Flash钓鱼配合MSF捆绑上线ctfshow XSS靶场练习 知识补充 SQL注入小迪讲解 文件上传小迪讲解 文件上传中间件解析 XSS跨站脚本 xss平台: https://xss.pt/ 原理 恶意攻击者…...

2024/2/12 图的基础知识 2
目录 查找文献 P5318 【深基18.例3】查找文献 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 有向图的拓扑序列 848. 有向图的拓扑序列 - AcWing题库 最大食物链计数 P4017 最大食物链计数 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 查找文献 P5318 【深基18.例3】…...

无人机飞行原理,多旋翼无人机飞行原理详解
多旋翼无人机升空飞行的首要条件是动力,有了动力才能驱动旋粪旋转,才能产生克服重力所必需的升力。使旋翼产生升力,进而推动多旋翼无人机升空飞行的一套设备装置称为动力装置,包括多旋翼无人机的发动机以及保证发动机正常工作所必…...
docker本地目录挂载
小命令 1、查看容器详情 docker inspect 容器名称 还是以nginx为例,上篇文章我们制作了nginx静态目录的数据卷,此时查看nginx容器时会展示出来(docker inspect nginx 展示信息太多,这里只截图数据卷挂载信息)&#…...
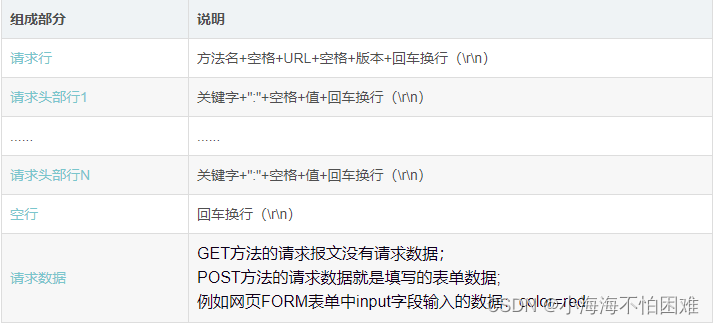
使用C++从零开始,自己写一个MiniWeb
第一步:新建项目 1、打开VS点击创建新项目 2、选择空项目并点下一步(切记不能选错项目类型) 3、填写项目名称和路径,点击创建即可 新建好后项目是这样的比较干净 4、右击源文件,点击添加,新建http.cpp文件…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
