计算机视觉基础:矩阵运算
矩阵及其表示方式
一个矩阵是由行(row)和列(column)组成的一个矩形数组,通常包含数字。我们可以用大写字母(如 A、B)来表示一个矩阵。例如,矩阵 A 可能看起来像这样:
A = [ a11 a12 a13 ][ a21 a22 a23 ][ a31 a32 a33 ]其中,a11是位于第一行第一列的元素,a12是第一行第二列的元素,以此类推。图像可以被看作是一个巨大的矩阵,其中每个像素点对应矩阵中的一个元素。
矩阵基础运算
- 矩阵加法和减法:矩阵的加减法是对应位置元素相加或相减。例如,如果有两个相同大小的矩阵 A 和 B,它们的加法 A+B 将产生一个新矩阵 C,其中 cij = aij + bij。
- 矩阵数乘:矩阵 A 与一个标量 k 的数乘是将 A 中的每个元素乘以 k。
矩阵乘法
矩阵乘法是线性代数中的一个核心操作,它在图像处理、计算机图形学以及数据科学的许多方面都非常重要。现在,我将更详细地解释矩阵乘法以及如何计算两个矩阵的产品。
矩阵乘法详解
当你乘以两个矩阵时,你其实是在将第一个矩阵的行与第二个矩阵的列组合。对于两个矩阵 A 和 B,矩阵 A 的列数必须等于矩阵 B 的行数才能进行乘法。
我们来逐步分析一下具体的操作步骤:
- 确认矩阵 A 的列数等于矩阵 B 的行数。
- 创建结果矩阵 C,其维度将是矩阵 A 的行数乘以矩阵 B 的列数(如果 A 是 m×n 维,B 是 n×p 维,那么 C 是 m×p 维)。
- 计算矩阵 C 的每个元素 cij。为了找到 cij,你需要取矩阵 A 的第 i 行和矩阵 B 的第 j 列。
- 将 A 的第 i 行与 B 的第 j 列上的对应元素进行相乘,并将乘积相加。这个总和就是矩阵 C 的元素 cij。
简单举例解释
使用一个 2×3 的矩阵 A 和一个 3×2 的矩阵 B。
A = [ a11 a12 a13 ] B = [ b11 b12 ][ a21 a22 a23 ] [ b21 b22 ][ b31 b32 ]令矩阵 A 和 B 为:
A = [ 1 2 3 ] B = [ 7 8 ][ 4 5 6 ] [ 9 0 ][ 1 2 ]根据矩阵乘法的规则,我们可以计算矩阵 A 和 B 的乘积 C,结果矩阵 C 的大小将是 2×2。我们现在按步骤计算,并将乘积算式放到结果矩阵 C 中:
C = [ (a11*b11 + a12*b21 + a13*b31) (a11*b12 + a12*b22 + a13*b32) ][ (a21*b11 + a22*b21 + a23*b31) (a21*b12 + a22*b22 + a23*b32) ]代入我们给定的矩阵:
C = [ (1*7 + 2*9 + 3*1) (1*8 + 2*0 + 3*2) ][ (4*7 + 5*9 + 6*1) (4*8 + 5*0 + 6*2) ]计算得到结果矩阵 C 的每个元素:
C = [ (7 + 18 + 3) (8 + 0 + 6) ][ (28 + 45 + 6) (32 + 0 + 12) ]将每个元素中的数值相加:
C = [ 28 14 ][ 79 44 ]所以,矩阵 A 和 B 的乘积 C 是:
C = [ 28 14 ][ 79 44 ]这就是矩阵乘法的结果。
稍复杂举例解释
我们让矩阵 A 是一个 2×3 的矩阵,矩阵 B 是一个 3×4 的矩阵。下面是 A 和 B 的示例:
A = [ a11 a12 a13 ] B = [ b11 b12 b13 b14 ][ a21 a22 a23 ] [ b21 b22 b23 b24 ][ b31 b32 b33 b34 ]由于矩阵 A 的大小是 2×3,矩阵 B 的大小是 3×4,矩阵 A 的列数和矩阵 B 的行数相同,我们可以计算出它们的乘积 C。结果矩阵 C 的大小将是 2×4。
让我们具体计算矩阵 A 和 B 的乘积,并将乘积算式直接写在结果矩阵 C 中。
C = [ (a11*b11 + a12*b21 + a13*b31) (a11*b12 + a12*b22 + a13*b32) (a11*b13 + a12*b23 + a13*b33) (a11*b14 + a12*b24 + a13*b34) ][ (a21*b11 + a22*b21 + a23*b31) (a21*b12 + a22*b22 + a23*b32) (a21*b13 + a22*b23 + a23*b33) (a21*b14 + a22*b24 + a23*b34) ]现在,我们来设定具体的数字来完成乘法:
A = [ 1 2 3 ] B = [ 2 0 1 4 ][ 4 5 6 ] [ 0 1 3 2 ][ 7 8 5 6 ]计算出结果矩阵 C 的每个元素:
C = [ (1*2 + 2*0 + 3*7) (1*0 + 2*1 + 3*8) (1*1 + 2*3 + 3*5) (1*4 + 2*2 + 3*6) ][ (4*2 + 5*0 + 6*7) (4*0 + 5*1 + 6*8) (4*1 + 5*3 + 6*5) (4*4 + 5*2 + 6*6) ]进行计算,我们得到:
C = [ (2 + 0 + 21) (0 + 2 + 24) (1 + 6 + 15) (4 + 4 + 18) ][ (8 + 0 + 42) (0 + 5 + 48) (4 + 15 + 30) (16 + 10 + 36) ]将 C 中的每个元素简化:
C = [ 23 26 22 26 ][ 50 53 49 62 ]所以,经过计算,我们得到的最终结果矩阵 C 是:
C = [ 23 26 22 26 ][ 50 53 49 62 ]这个结果就是我们从矩阵 A 和 B 计算得到的乘积。
练习
假设我们有两个矩阵 A 和 B:
A = [1 2] B = [5 6][3 4] [7 8]矩阵 A 是一个 2×2 的矩阵,矩阵 B 也是一个 2×2 的矩阵。它们的乘积 AB 将产生另一个 2×2 的矩阵 C。那么 C 就是:
C = [ c11 c12 ][ c21 c22 ]我们现在来计算 C 的每一个元素。
- 计算 c11:
我们取 A 的第一行 [1 2] 和 B 的第一列 [5 7],
之后将对应元素相乘并相加:1×5 + 2×7 = 5 + 14 = 19。 - 计算 c12:
我们取 A 的第一行 [1 2] 和 B 的第二列 [6 8],
之后将对应元素相乘并相加:1×6 + 2×8 = 6 + 16 = 22。 - 计算 c21:
我们取 A 的第二行 [3 4] 和 B 的第一列 [5 7],
之后将对应元素相乘并相加:3×5 + 4×7 = 15 + 28 = 43。 - 计算 c22:
我们取 A 的第二行 [3 4] 和 B 的第二列 [6 8],
之后将对应元素相乘并相加:3×6 + 4×8 = 18 + 32 = 50。
所以,矩阵 C 就是:
C = [19 22][43 50]这就完成了矩阵 A 和 B 的乘积。
矩阵乘法不符合交换律,也就是说,通常 AB ≠ BA。这是计算矩阵乘积时要特别注意的一点。
理解好矩阵乘法之后,在处理图像时,你会经常用到它来进行变换、过滤和其他操作。希望这个例子能够帮助你理解矩阵乘法的具体过程。
单位矩阵和逆矩阵
- 单位矩阵:是一个特殊的方阵,其所有对角线上的元素都是 1,其余元素都是 0,记为 I。例如:
I = [ 1 0 0 ][ 0 1 0 ][ 0 0 1 ]- 逆矩阵:对于一个方阵 A,如果存在另一个方阵 B,使得 AB = BA = I,则我们说 B 是 A 的逆矩阵,记作 A^(-1)。不是所有矩阵都有逆矩阵,只有那些行列式(determinant)不为 0 的方阵才有逆矩阵。
矩阵的转置
转置操作将矩阵的行和列交换位置。对于矩阵 A,它的转置记为 A^T。A 的一个元素 aij 在 A^T 中的位置变成了 aji。
例如,如果有矩阵 A:
A = [ 1 2 ][ 3 4 ]那么 A^T 就是:
A^T = [ 1 3 ][ 2 4 ]相关文章:

计算机视觉基础:矩阵运算
矩阵及其表示方式 一个矩阵是由行(row)和列(column)组成的一个矩形数组,通常包含数字。我们可以用大写字母(如 A、B)来表示一个矩阵。例如,矩阵 A 可能看起来像这样: A [ a11 a12 a13 ][ a21 a22 a23 ][ a31 a32 a3…...

Gateway中Spring Security6统一处理CORS
文章目录 一、起因二、解决方法 一、起因 使用了gateway微服务作为整体的网关,并且整合了Spring Security6;还有一个system微服务,作为被请求的资源,当浏览器向gateway发送请求,请求system资源时,遇到CORS…...
)
突破编程_C++_基础教程(输入、输出与文件)
1 流和缓冲区 C中,流( stream )和缓冲区( buffer )是两个紧密相关的概念,它们在处理输入和输出时起着重要的作用。 流( Stream ) 流是一种抽象的概念,用于表示数据的流动…...

UE的 HUD 类中的必备方法和属性
在屏幕上绘制的方法 1. DrawText() DrawText() 方法允许开发者在屏幕上渲染文本。参数包括文本内容、位置、颜色、字体、缩放等。 void DrawText(const FString& Text, const FLinearColor& TextColor, float ScreenX, float ScreenY, UFont* Font, float Scale 1.…...
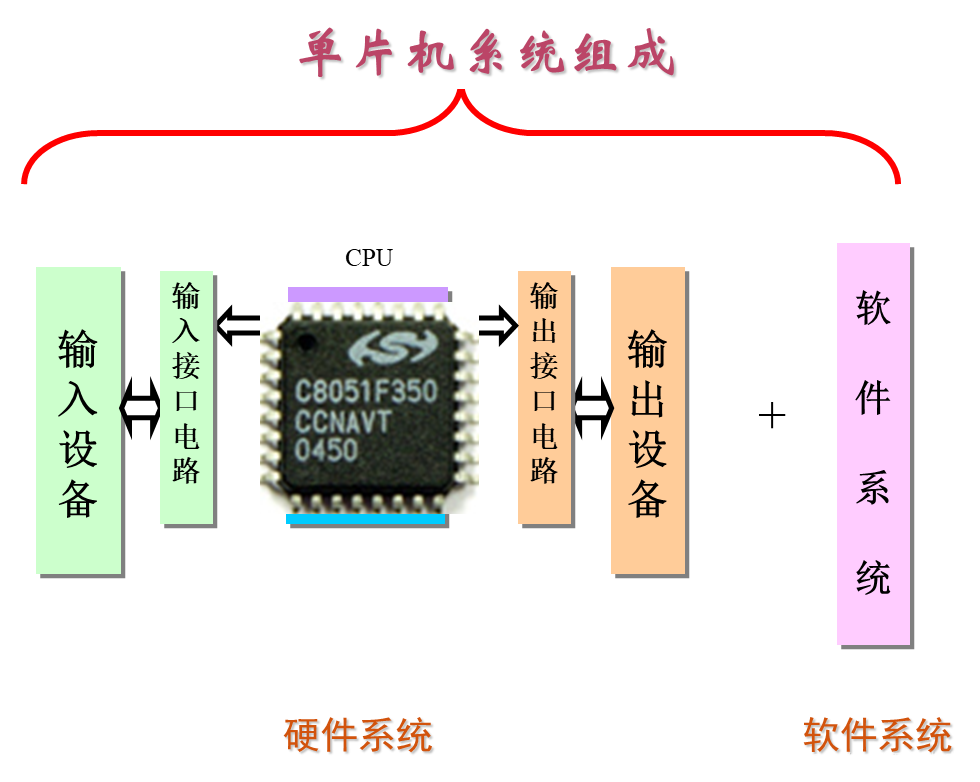
单片机的认识
单片机的定义 先简单理解为: 在一片集成电路芯片上集成了微处理器(CPU )存储器(ROM和RAM)、I/O 接口电路,构成单芯片微型计算机,即为单片机。 把组成微型计算机的控制器、运算器、存储器、输…...

转发:udig安装 用来为geoserver上shp地图配置显示样式 颜色
下载udig,解压缩 这东东是基于eclipse的,需要Java JRE 把 JDK 1.8 里面的jre目录拷贝到 udig目录下面 udig下载、安装及汉化,简单生成geoserver图层样式sld-CSDN博客...

Linux--常用命令(详解)
详细目录 一、终端命令格式二、显示文件列表命令-ls2.1作用2.2格式2.3 ls常用选项2.3.1 ls -a2.3.2 ls -l(等价于 ll)2.3.2 ls -h 三、相对路径与绝对路径3.1绝对路径3.2相对路径 四、目录操作命令 -cd4.1作用4.2格式4.3案例4.3.1 cd -: 返回上一次所在目录4.3.2 cd…...

SouthLeetCode-打卡24年02月第1周
SouthLeetCode-打卡24年02月第1周 // Date : 2024/02/01 ~ 2024/02/04 034.合并两个有序链表 (1) 题目描述 034#LeetCode.21.#北岸计划2024/02/01 将两个升序链表合并为一个新的 升序 链表并返回。 新链表是通过拼接给定的两个链表的所有节点组成的。 (2) 题解代码 cla…...

vscode的cmake工具小三角符号旁边没有目标的解决方法
vscode里面写了个项目,找了半天没办法用cmake调试,最后发现是cmake里面的set(CMAKE_BUILD_TYPE Release)导致的,都是release模式了当然不能调试了;改成Debug就行了 参考:https://stackoverflow.com/questions/7549672…...

Servlet JSP-Eclipse安装配置Maven插件
Maven 是一款比较常用的 Java 开发拓展包,它相当于一个全自动 jar 包管理器,会导入用户开发时需要使用的相应 jar 包。使用 Maven 开发 Java 程序,可以极大提升开发者的开发效率。下面我就跟大家介绍一下如何在 Eclipse 里安装和配置 Maven 插…...

os模块
os 模块是 Python 中用于与操作系统进行交互的标准库之一。它提供了许多函数来执行文件和目录操作,管理进程以及与操作系统交互的其他功能。 下面是一些 os 模块中常用的函数和功能: 文件和目录操作: os.getcwd(): 返回当前工作目录的路径。…...
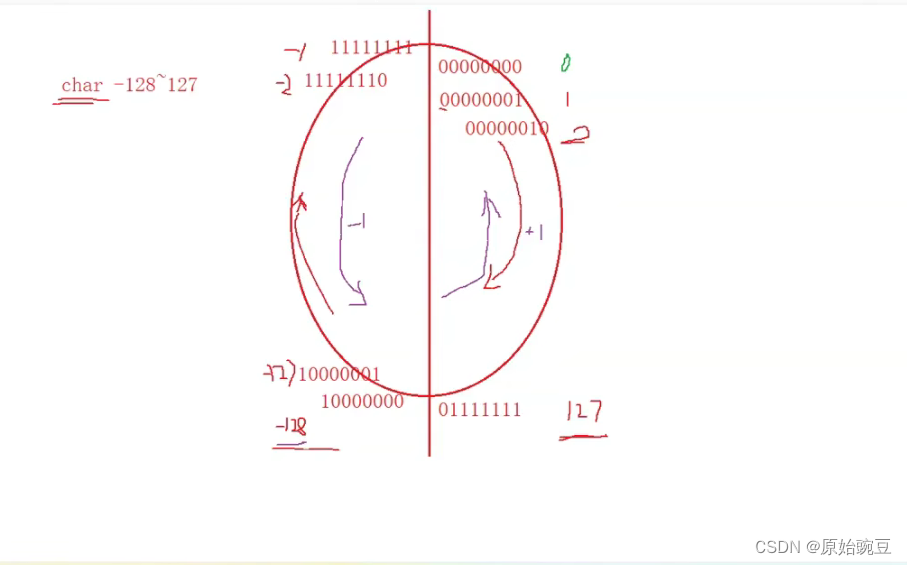
【C语言进阶】深度剖析数据在内存中的存储--上
1. C语言中的数据类型的简单介绍 注:C99标准里面,定义了bool类型变量。这时,只要引入头文件stdbool.h ,就能在C语言里面正常使用bool类型。 1.1 在C语言中各类型所占内存空间的大小如下 char类型的数据类型大小为1字节即8比特位。…...

【doghead】VS2022 win11 安装配置WSL2 以编译linux端的cmake项目并运行2
【bifrost】VS2022 win11 安装配置WSL2 以编译linux端的cmake项目并运行1 完成了WSL2的安装。13900K 的电脑安装了ubuntu22.04构建中出现了一些问题,fix了。发现libuv 似乎不识别,认为是libuv.so ,无法让worker识别到uv 从而没构建。干脆单独构建好了,官方的脚本如此:而且…...

【教程】C++语言基础学习笔记(七)——Array数组
写在前面: 如果文章对你有帮助,记得点赞关注加收藏一波,利于以后需要的时候复习,多谢支持! 【C语言基础学习】系列文章 第一章 《项目与程序结构》 第二章 《数据类型》 第三章 《运算符》 第四章 《流程控制》 第五章…...
BUGKU-WEB GET
题目描述 没有提示,就一个get,启动场景看看: 解题思路 显然是PHP语言解读分析代码吧写出你的payload 相关工具 略 解题步骤 进入场景分析代码 $what$_GET[what]; echo $what; if($whatflag) echo flag{****};前两句:使用get…...

蓝桥杯每日一题----唯一分解定理
唯一分解定理 1.内容 任何一个大于1的整数n都可以分解成若干个质数的连乘积,如果不计各个质数的顺序,那么这种分解是惟一的,即若n>1,则有 n ∏ p i j n\prod{p^j_i} n∏pij 这里的 p i p_i pi是质数。可以进行简单证明…...

openssl3.2 - osslsigncode工程的学习
文章目录 openssl3.2 - osslsigncode工程的学习概述笔记工程库地址工程的编译osslsigncodeM工程文件列表osslsigncodeM工程搭建细节原始工程实现的改动自己封装的包含openssl和curl的实现osslsigncodeM工程命令行的用法备注 - VS2019调试环境备注 - 如果要单步openssl的API学学…...
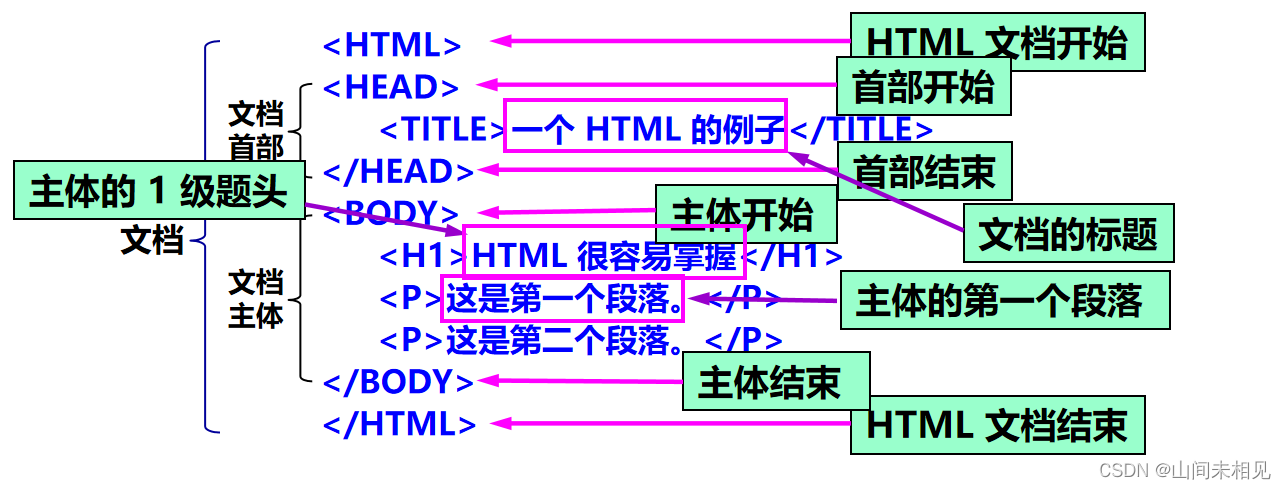
HTML 超文本标记语言
超文本标记语言 HTML 在一个客户程序主窗口上显示出的万维网文档称为页面 (page)。 页面制作的标准语言:HTML。 超文本标记语言 HTML (HyperText Markup Language) 是一种制作万维网页面的标准语言,它消除了不同计算机之间信息交流的障碍,…...

sklearn:机器学习 分类特征编码category_encoders
文章目录 category_encoders简介OrdinalEncoder 序列编码OneHotEncoder 独热编码TargetEncoder 目标编码Binary Encoder 二进制编码BaseNEncoder 贝叶斯编码LeaveOneOutEncoder 留一法HashingEncoder 哈希编码CatBoostEncoder catboost目标编码CountEncoder 频率编码WOEEncoder…...
‘ is ambiguous)
C++错误[错误] call of overloaded ‘min(int, int)‘ is ambiguous
错误代码: #include<iostream> using namespace std;template <class T> T min(T x,T y){if(x<y){return x;}else return y; }int main(){int n12,n210;double d11.5,d25.6;cout<<min(n1,n2)<<endl;cout<<min(d1,d2)<<endl…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

虚幻基础:角色旋转
能帮到你的话,就给个赞吧 😘 文章目录 移动组件使用控制器所需旋转:组件 使用 控制器旋转将旋转朝向运动:组件 使用 移动方向旋转 控制器旋转和移动旋转 缺点移动旋转:必须移动才能旋转,不移动不旋转控制器…...
)
stm32进入Infinite_Loop原因(因为有系统中断函数未自定义实现)
这是系统中断服务程序的默认处理汇编函数,如果我们没有定义实现某个中断函数,那么当stm32产生了该中断时,就会默认跑这里来了,所以我们打开了什么中断,一定要记得实现对应的系统中断函数,否则会进来一直循环…...

性能优化中,多面体模型基本原理
1)多面体编译技术是一种基于多面体模型的程序分析和优化技术,它将程序 中的语句实例、访问关系、依赖关系和调度等信息映射到多维空间中的几何对 象,通过对这些几何对象进行几何操作和线性代数计算来进行程序的分析和优 化。 其中࿰…...
