产品经理面试题解析:业务架构是通往成功的关键吗?

大家好,我是小米!今天我要和大家聊的是产品经理面试中的一个热门话题:“业务架构”!相信不少小伙伴在准备面试的时候都会遇到这个问题,究竟什么是业务架构?它又与产品经理的工作有着怎样的关系呢?让我们一起来揭开这个神秘的面纱吧!
什么是业务架构?
首先,让我们来理解一下“业务架构”的概念。简单来说,业务架构是指企业在发展过程中所采用的商业模式、组织结构、流程规范等的组合。它旨在确保企业的各项业务活动能够有序进行,实现整体战略目标。
具体来说,业务架构包括以下几个方面:
- 商业模式:指企业的盈利模式、市场定位、竞争策略等,决定了企业的核心业务方向和发展路径。
- 组织结构:包括企业内部各个部门的划分、职责分工以及上下级关系等,影响着信息流、决策流和执行流程。
- 流程规范:指企业内部各种业务活动的标准化流程和操作规范,确保业务的高效运转和质量保障。
- 信息系统:作为支撑业务运作的基础设施,包括企业内部的管理系统、数据平台等,为业务的数字化转型提供支持
业务架构的建立和优化,对企业的发展至关重要。它能够帮助企业更好地理解自身的定位和发展方向,提升组织的灵活性和适应能力,从而在竞争激烈的市场中立于不败之地。
业务架构与产品经理的关系
那么,业务架构与产品经理的工作又有着怎样的联系呢?其实,业务架构是产品经理在日常工作中需要密切关注和理解的一个重要方面。
- 理解业务需求:作为产品经理,我们需要深入了解企业的业务架构,掌握核心业务流程和关键环节,以便更准确地把握用户需求,指导产品设计和优化。
- 跨部门协作:业务架构涉及到企业内部各个部门之间的协同配合,而产品经理往往需要作为连接不同部门的桥梁,推动产品的顺利开发和推广。
- 产品规划与落地:在产品规划阶段,产品经理需要结合业务架构的特点和需求,制定相应的产品策略和路线图;在产品落地阶段,又需要与技术团队密切合作,确保产品能够顺利上线并满足业务需求。
- 持续优化与创新:业务架构的不断演进也会带来产品需求的变化,作为产品经理,我们需要及时调整产品方向,持续优化产品体验,保持创新竞争力
因此,可以说,业务架构和产品经理的工作密切相关,相辅相成。只有深入理解和把握业务架构,产品经理才能更好地发挥自己的作用,推动企业的持续发展。
如何准备业务架构面试题?
最后,我想和大家分享一些准备业务架构面试题的小建议:
- 学习基础知识:首先要对业务架构的基本概念和原理有所了解,可以通过阅读相关书籍、文章或者参加相关培训来提升自己的知识水平。
- 案例分析实践:通过分析一些真实的企业案例,了解它们的业务架构设计和优化实践,可以帮助我们更好地理解理论知识,并且能够在面试中举一反三。
- 与行业专家交流:可以通过参加行业活动、线上论坛或者社交媒体平台,与行业专家和同行进行交流,分享经验和心得,拓展自己的视野。
- 模拟面试练习:最后,可以找一些朋友或者同事进行模拟面试,模拟真实的面试场景,检验自己的业务架构能力和表达能力,并且及时吸收他人的反馈意见,不断提升自己
通过以上几点的努力,相信大家一定能够在业务架构面试中游刃有余,展现出自己的专业能力和个人魅力!
结语
今天我们通过探讨“业务架构”这个话题,不仅对产品经理的工作有了更深入的理解,也为我们在面试中更加从容自信地回答相关问题提供了一些思路和方法。
希望小伙伴们能够从中受益,不断提升自己的专业素养和综合能力,成为行业中的佼佼者!如果大家对这个话题还有什么疑问或者想法,欢迎在评论区留言,我会及时回复哒~
END
最后,祝大家在未来的面试中取得好成绩,早日实现自己的职业目标!感谢大家的阅读,我们下期再见!
如有疑问或者更多的技术分享,欢迎关注我的微信公众号“知其然亦知其所以然”!
相关文章:

产品经理面试题解析:业务架构是通往成功的关键吗?
大家好,我是小米!今天我要和大家聊的是产品经理面试中的一个热门话题:“业务架构”!相信不少小伙伴在准备面试的时候都会遇到这个问题,究竟什么是业务架构?它又与产品经理的工作有着怎样的关系呢࿱…...

【蓝桥杯】灭鼠先锋
一.题目描述 二.解题思路 博弈论: 只能转移到必胜态的,均为必败态。 可以转移到必败态的,均为必胜肽。 最优的策略是,下一步一定是必败态。 #include<iostream> #include<map> using namespace std;map<string,bo…...
)
2024年华为OD机试真题-求字符串中所有整数的最小和-Python-OD统一考试(C卷)
题目描述: 输入字符串s,输出s中包含所有整数的最小和 说明 1. 字符串s,只包含 a-z A-Z +- ; 2. 合法的整数包括 1) 正整数 一个或者多个0-9组成,如 0 2 3 002 102 2)负整数 负号 - 开头,数字部分由一个或者多个0-9组成,如 -0 -012 -23 -00023 输入描述: 包含…...
数据分析基础之《pandas(7)—高级处理2》
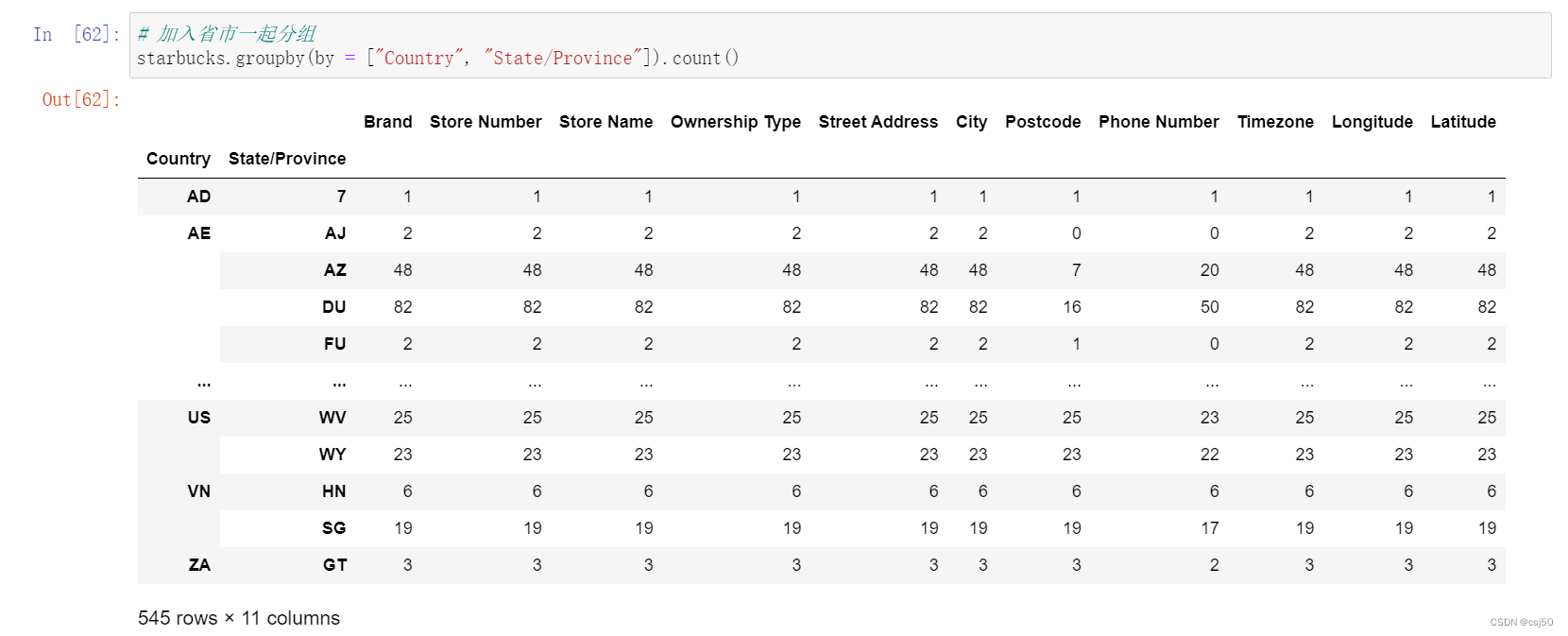
四、合并 如果数据由多张表组成,那么有时候需要将不同的内容合并在一起分析 1、先回忆下numpy中如何合并 水平拼接 np.hstack() 竖直拼接 np.vstack() 两个都能实现 np.concatenate((a, b), axis) 2、pd.concat([data1, data2], axis1) 按照行或者列…...

fluent脱硝SCR相对标准偏差、氨氮比、截面速度计算
# -*- coding: utf-8 -*- """ Created on Wed Sep 20 20:40:30 2023 联系QQ:3123575367,专业SCR脱硝仿真。 该程序用来处理fluent通过export-solution-ASCII-Space导出的数据,可计算标准偏差SD、相对标准偏差RSD,适用于求解平面的相对均匀…...
(A~E))
Codeforces Round 925 (Div. 3)(A~E)
题目暂时是AC,现在是Hack阶段,代码仅供参考。 A. Recovering a Small String 题目给出的n都可以由字母来组成,比如4可以是aab,字母里面排第一个和第二个,即1124。但是会歧义,比如aba为1214,也是…...

@RequestBody、@RequestParam、@RequestPart使用方式和使用场景
RequestBody和RequestParam和RequestPart使用方式和使用场景 1.RequestBody2.RequestParam3.RequestPart 1.RequestBody 使用此注解接收参数时,适用于请求体格式为 application/json,只能用对象接收 2.RequestParam 接收的参数是来自HTTP 请求体 或 请…...
LeetCode、1143. 最长公共子序列【中等,二维DP】
文章目录 前言LeetCode、1143. 最长公共子序列【中等,二维DP】题目链接与分类思路2022年暑假学习思路及题解二维DP解决 资料获取 前言 博主介绍:✌目前全网粉丝2W,csdn博客专家、Java领域优质创作者,博客之星、阿里云平台优质作者…...
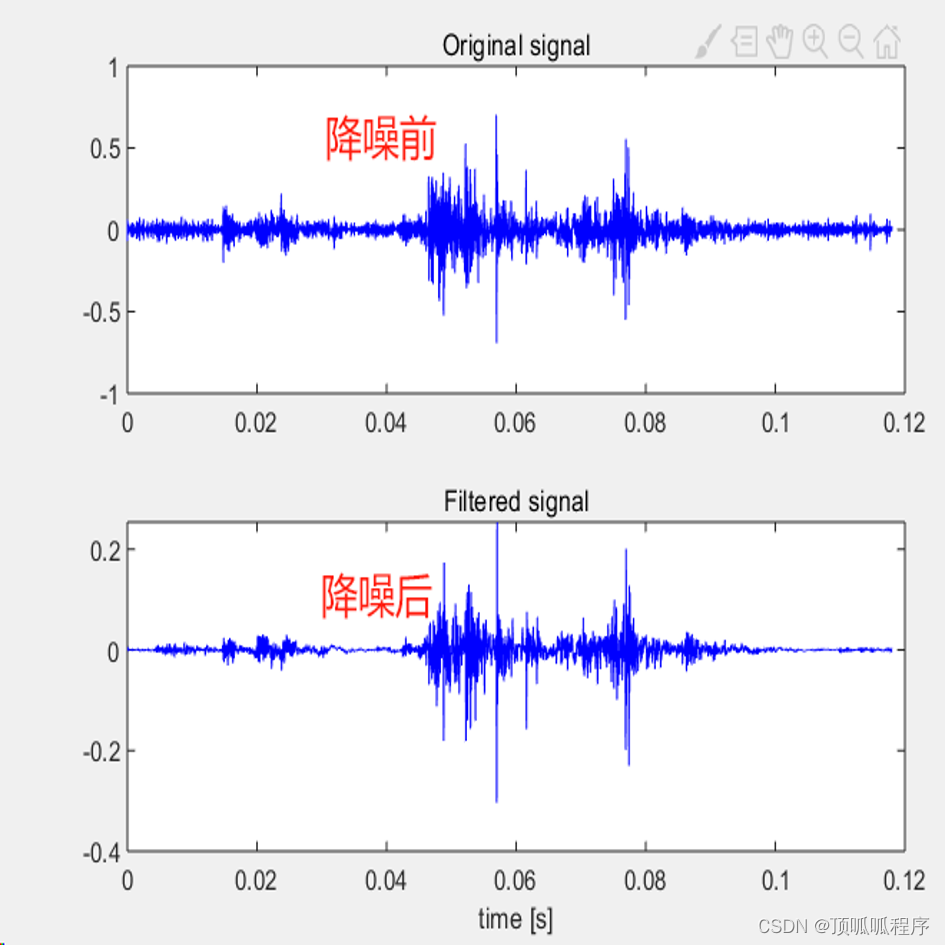
162基于matlab的多尺度和谱峭度算法对振动信号进行降噪处理
基于matlab的多尺度和谱峭度算法对振动信号进行降噪处理,选择信号峭度最大的频段进行滤波,输出多尺度谱峭度及降噪结果。程序已调通,可直接运行。 162 matlab 信号处理 多尺度谱峭度 (xiaohongshu.com)...

Android Studio六大基本布局的概览和每个布局的关键特性以及实例分析
1. 线性布局 (LinearLayout) 描述: 线性布局是一种按指定方向(水平或垂直)排列其子视图的布局容器。通过android:orientation属性可设置为horizontal或vertical。 关键属性: android:orientation: 指定布局方向。android:layout_weight: 子视图权重,用于分配剩余空间。示…...

【go语言】一个简单HTTP服务的例子
一、Go语言安装 Go语言(又称Golang)的安装过程相对简单,下面是在不同操作系统上安装Go语言的步骤: 在Windows上安装Go语言: 访问Go语言的官方网站(golang.org)或者使用国内镜像站点࿰…...

LeetCode Python - 15.三数之和
目录 题目答案运行结果 题目 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意:答案中不可…...
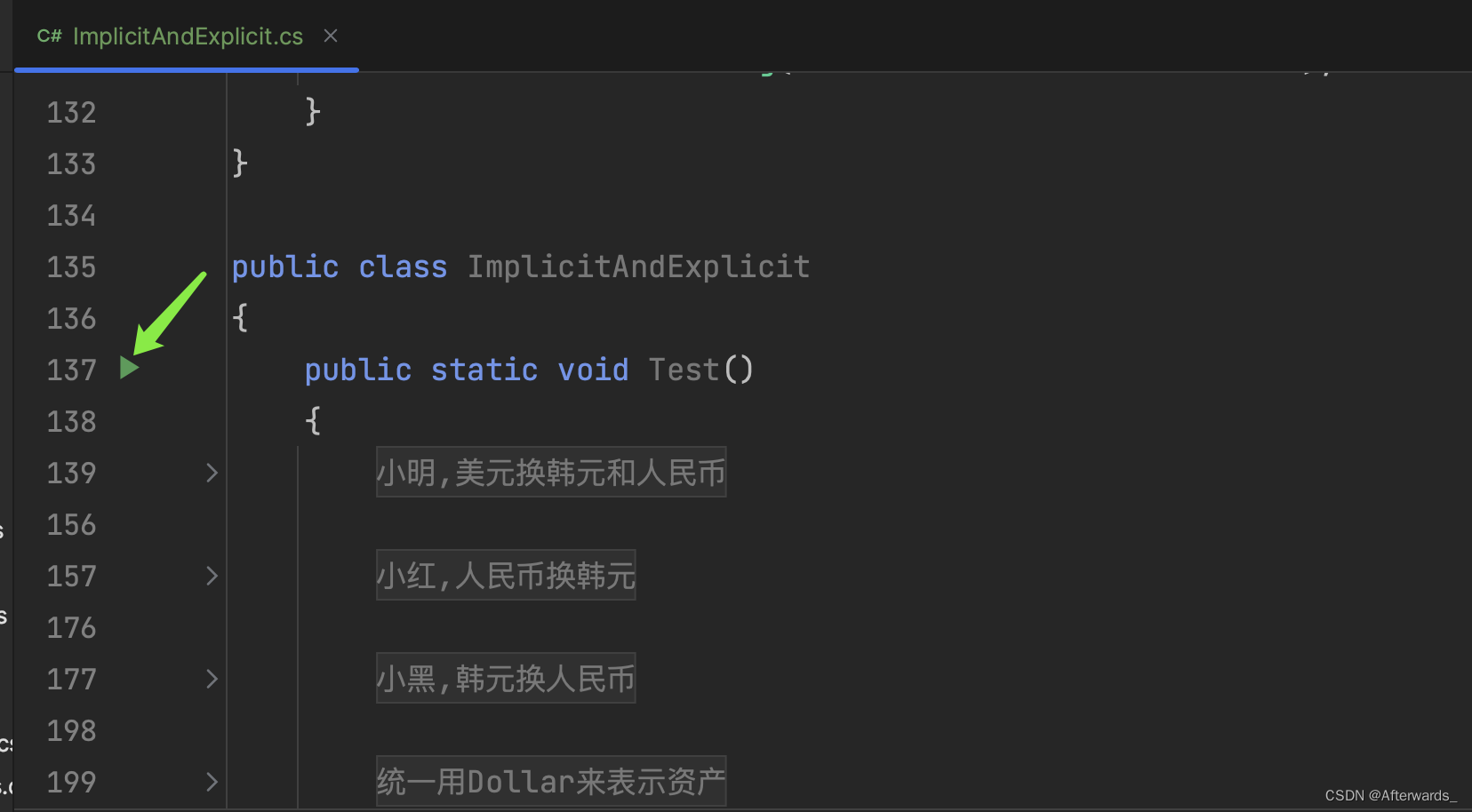
C#中implicit和explicit
理解: 使用等号代替构造函数调用的效果以类似重载操作符的形式定义用于类型转换的函数前者类型转换时候直接写等号赋值语法,后者要额外加目标类型的强制转换stirng str -> object o -> int a 可以 int a (int)(str as object)转换通过编译,但没有转换逻辑所以运行会报错…...

探讨java系统中全局唯一ID实现方案
为什么需要全局唯一ID 我们这里引用美团 Leaf 的场景介绍:在复杂分布式系统中,往往需要对大量的数据和消息进行唯一标识。如在美团点评的金融、支付、餐饮、酒店、猫眼电影等产品的系统中,数据日渐增长,对数据分库分表后需要有一…...
微信小程序(四十四)鉴权组件插槽-登入检测
注释很详细,直接上代码 新增内容: 1.鉴权组件插槽的用法 2.登入检测示范 源码: app.json {"usingComponents": {"auth":"/components/auth/auth"} }app.js App({globalData:{//定义全局变量isLoad:false} })…...
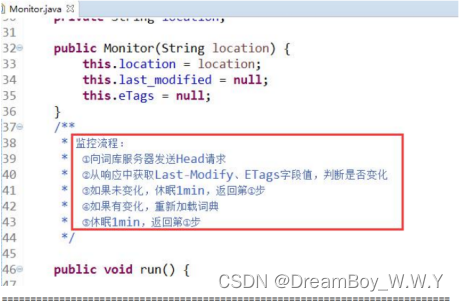
【ES】--ES集成热更新自定义词库(字典)
目录 一、问题描述二、具体实施1、Tomcat实现远程扩展字典2、验证生效3、ES配置远程扩展字典4、为何不重启ES能实现热更新 一、问题描述 问题现象: 前面完成了自定义分词器词库集成到ES中。在实际项目中词库是时刻在变更的,但又不希望重启ES,对此我们应…...

能源管理师——为能源可持续发展护航
能源管理师是在能源管理领域具有专业知识和技能的专业人士,他们的工作对于实现能源的有效利用和可持续发展至关重要。 能源管理师的主要职责是协助企业或组织进行能源管理,包括能源规划、能源审计、节能措施的实施和能源绩效的评估等。他们通过对能源使…...

设计模式理解:单例模式+工厂模式+建设者模式+原型模式
迪米特法则:Law of Demeter, LoD, 最少知识原则LKP 如果两个软件实体无须直接通信,那么就不应当发生直接的相互调用,可以通过第三方转发该调用。其目的是降低类之间的耦合度,提高模块的相对独立性。 所以,在运用迪米特…...

DataX源码分析 writer
系列文章目录 一、DataX详解和架构介绍 二、DataX源码分析 JobContainer 三、DataX源码分析 TaskGroupContainer 四、DataX源码分析 TaskExecutor 五、DataX源码分析 reader 六、DataX源码分析 writer 七、DataX源码分析 Channel 文章目录 系列文章目录前言DataX的Writer写入流…...

为自己的项目媒体资源添加固定高度
为自己的项目媒体资源添加固定高度 未媒体资源添加固定高度,不仅有利于确定懒加载后的切确位置,还可以做骨架屏、loading动画等等,但是因为历史数据中很多没有加高度的媒体资源,所以一直嫌麻烦没有做。 直到这个季度有一个自上而…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
