【数据结构】二叉树的顺序结构及链式结构
目录
1.树的概念及结构
1.1树的概念
1.2树的相关概念
编辑
1.3树的表示
1.4树在实际中的运用(表示文件系统的目录树结构)
2.二叉树概念及结构
2.1二叉树的概念
2.2现实中的二叉树
编辑
2.3特殊的二叉树
2.4二叉树的性质
2.5二叉树的存储结构
3 .二叉树链式结构的实现
3.1二叉树的创建
3.2二叉树的遍历
3.21前序、中序以及后序遍历
3.22层序遍历
1.树的概念及结构
1.1树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因 为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
- 有一个特殊的结点,称为根结点,根节点没有前驱结点
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 因此,树是递归定义的。

注意:树形结构中,子树之间不能有交集,否则就不是树形结构

1.2树的相关概念
- 节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
- 叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
- 非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
- 兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
- 树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
- 节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
- 森林:由m(m>0)棵互不相交的树的集合称为森林;
1.3树的表示
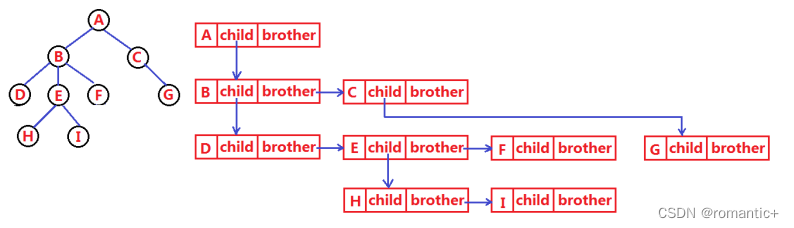
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间 的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法 等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一个孩子结点struct Node* _pNextBrother; // 指向其下一个兄弟结点DataType _data; // 结点中的数据域
};
1.4树在实际中的运用(表示文件系统的目录树结构)

2.二叉树概念及结构
2.1二叉树的概念
一颗二叉树的节点是一个有限的集合,该集合只有俩种可能:
1.为空指针
2.由一个根节点和俩个分别称为左子树和右子树的二叉组成

由上图可知:
1. 二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树 注意:对于任意的二叉树都是由以下几种情况复合而成的:
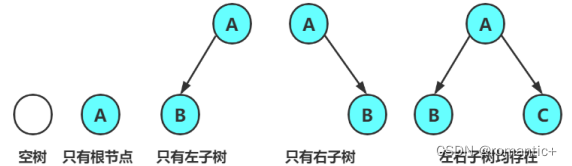
2.2现实中的二叉树

2.3特殊的二叉树
1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是 说,如果一个二叉树的层数为K,且结点总数是2的k次方-1 ,则它就是满二叉树。
2. 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K 的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对 应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
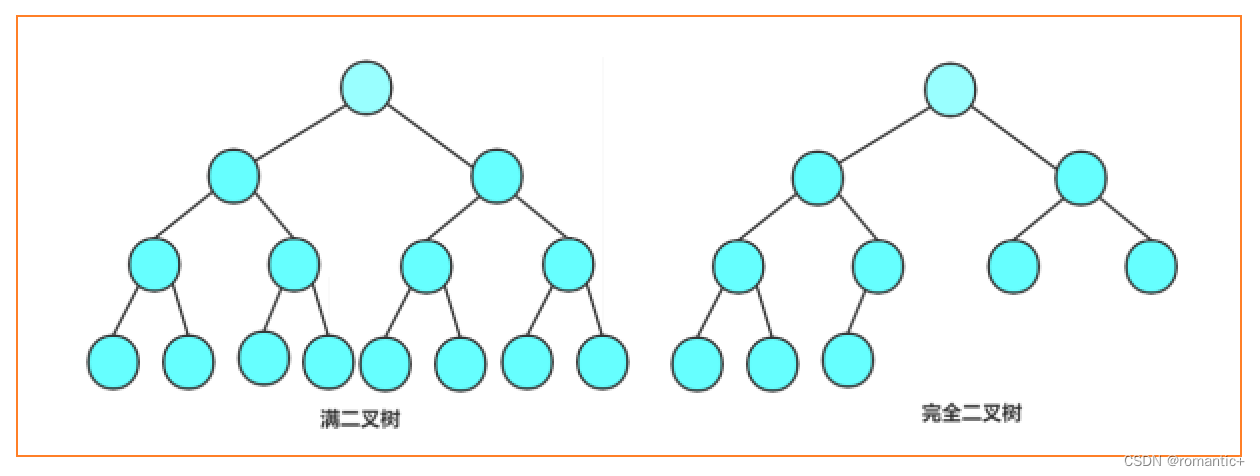
2.4二叉树的性质
1.若规定根节点的层数为1,则一颗非空二叉树的第i层最多有2(^2^-1)个结点。
2.若规定根节点的层数为1,则深度为h的二叉树的最大节点数是2(^h^)-1.
3.堆任何一颗二叉树,如果度为0其叶结点个数为n0,度为2的分支结点个数为n2,则有n0=n2+1.
4.若规定根节点的层数为1,则有n个结点的满二叉树的深度,h=log2(n+1).(ps:log2(n+1)是以2为底,n+1为对数)
5.对于具有n个节点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的节点有:
1. 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
2. 若2i+1=n否则无左孩子
3. 若2i+2=n否则无右孩子
2.5二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
1. 顺序存储 :顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们前面的章节有专门讲解。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
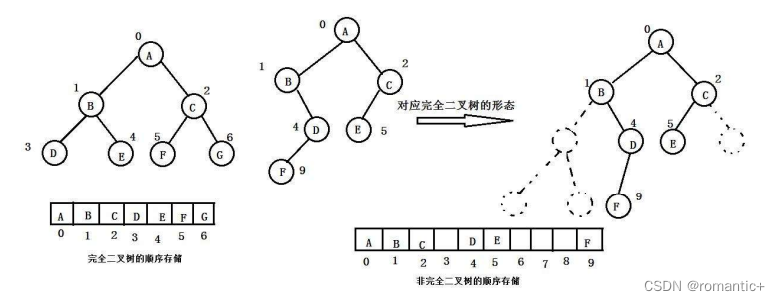
2. 链式存储 :二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链,后面会学到高阶数据结构如红黑树等会用到三叉链。

typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{struct BinTreeNode* _pLeft; // 指向当前节点左孩子struct BinTreeNode* _pRight; // 指向当前节点右孩子BTDataType _data; // 当前节点值域
}
// 三叉链
struct BinaryTreeNode
{struct BinTreeNode* _pParent; // 指向当前节点的双亲struct BinTreeNode* _pLeft; // 指向当前节点左孩子struct BinTreeNode* _pRight; // 指向当前节点右孩子BTDataType _data; // 当前节点值域
};
3 .二叉树链式结构的实现
3.1二叉树的创建
首先,我们这里先简单创建一个以中序遍历的二叉树结构,可以使用前序,中序,后序,下面会具体讲到遍历。
typedef struct BTNode
{char _data;struct BTNode* _left;struct BTNode* _right;
}BTNode;//中序遍历
void Inorder(BTNode* root)
{if(root){Inorder(root->_left);printf("%c ", root->_data);Inorder(root->_right);}
}BTNode* CreatBTree(char* str, int* pi)
{if(str[*pi]!= '#'){//当前节点非空,则创建当前节点BTNode*root=(BTNode*)malloc(sizeof(BTNode));root->_data = str[*pi];//字符位置向后移动一个位置++(*pi);//创建左子树root->_left=CreatBTree(str,pi);//字符位置向后移动一个位置++(*pi);//创建右子树root->_right=CreatBTree(str,pi);return root;}elsereturn NULL; //如果是空节点,则返回NULL
}int main()
{char str[101];int i = 0;//读入字符串scanf("%s", str);//创建二叉树BTNode* root = CreatBTree(str, &i);//中序打印二叉树Inorder(root);printf("\n");return 0;
}
3.2二叉树的遍历
3.21前序、中序以及后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。

按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为 根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
// 二叉树前序遍历
void PreOrder(BTNode* root);
// 二叉树中序遍历
void InOrder(BTNode* root);
// 二叉树后序遍历
void PostOrder(BTNode* root);
前序,中序和后序遍历图解:

3.22层序遍历
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在 层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层 上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
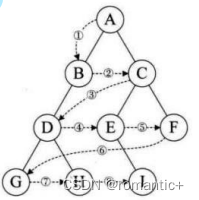
// 层序遍历
void LevelOrder(BTNode* root);
相关文章:

【数据结构】二叉树的顺序结构及链式结构
目录 1.树的概念及结构 1.1树的概念 1.2树的相关概念 编辑 1.3树的表示 1.4树在实际中的运用(表示文件系统的目录树结构) 2.二叉树概念及结构 2.1二叉树的概念 2.2现实中的二叉树 编辑 2.3特殊的二叉树 2.4二叉树的性质 2.5二叉树的存储结…...

海外IP代理:解锁网络边界的实战利器
文章目录 引言:正文:一、Roxlabs全球IP代理服务概览特点:覆盖范围:住宅IP真实性:性价比:在网络数据采集中的重要性: 二、实战应用案例一:跨境电商竞品分析步骤介绍:代码示…...

如何写好一个简历
如何编写求职简历 论Java程序员求职中简历的重要性 好简历的作用 在求职过程中,一份好的简历是非常重要的,它甚至可以直接决定能否被面试官认可。一份出色或者说是成功的个人简历,最根本的作用是能让看这份简历的人产生一定要见你的强烈愿…...
【AutoML】AutoKeras 进行 RNN 循环神经网络训练
由于最近这些天都在人工审查之前的哪些问答数据,所以迟迟都没有更新 AutoKeras 的训练结果。现在那部分数据都已经整理好了,20w 的数据最后能够使用的高质量数据只剩下 2k。这 2k 的数据已经经过数据校验并且对部分问题的提问方式和答案内容进行了不改变…...

H12-821_74
74.在某路由器上查看LSP,看到如下结果: A.发送目标地址为3.3.3.3的数据包时,打上标签1026,然后发送。 B.发送目标地址为4.4.4.4的数据包时,不打标签直接发送。 C.当路由器收到标签为1024的数据包,将把标签…...

有趣儿的组件(HTML/CSS)
分享几个炫酷的组件,起飞~~ 评论区留爪,继续分享哦~ 文章目录 1. 按钮2. 输入3. 工具提示4. 单选按钮5. 加载中 1. 按钮 HTML: <button id"btn">Button</button>CSS: button {padding: 10px 20px;text-tr…...
1、深度学习环境配置相关下载地址整理(cuda、cudnn、torch、miniconda、pycharm、torchvision等)
一、深度学习环境配置相关: 1、cuda:https://developer.nvidia.com/cuda-toolkit-archive 2、cudnn:https://developer.nvidia.com/rdp/cudnn-archive 4、miniconda:https://mirrors.tuna.tsinghua.edu.cn/anaconda/miniconda/?C…...
Spring Boot3自定义异常及全局异常捕获
⛰️个人主页: 蒾酒 🔥系列专栏:《spring boot实战》 🌊山高路远,行路漫漫,终有归途。 目录 前置条件 目的 主要步骤 定义自定义异常类 创建全局异常处理器 手动抛出自定义异常 前置条件 已经初始化好一个…...
【python】网络爬虫与信息提取--Beautiful Soup库
Beautiful Soup网站:https://www.crummy.com/software/BeautifulSoup/ 作用:它能够对HTML.xml格式进行解析,并且提取其中的相关信息。它可以对我们提供的任何格式进行相关的爬取,并且可以进行树形解析。 使用原理:它能…...

谷歌浏览器,如何将常用打开的网站创建快捷方式到电脑桌面?
打开谷歌浏览器,打开想要创建的快捷方式的网页 点击浏览器右上角的三个点: 点击选择【更多工具】 选择【创建快捷方式】 然后,在浏览器上方会弹出一个框,让命名此创建的快捷方式的名称 命名好之后,再点击【创…...

产品经理面试题解析:业务架构是通往成功的关键吗?
大家好,我是小米!今天我要和大家聊的是产品经理面试中的一个热门话题:“业务架构”!相信不少小伙伴在准备面试的时候都会遇到这个问题,究竟什么是业务架构?它又与产品经理的工作有着怎样的关系呢࿱…...

【蓝桥杯】灭鼠先锋
一.题目描述 二.解题思路 博弈论: 只能转移到必胜态的,均为必败态。 可以转移到必败态的,均为必胜肽。 最优的策略是,下一步一定是必败态。 #include<iostream> #include<map> using namespace std;map<string,bo…...
)
2024年华为OD机试真题-求字符串中所有整数的最小和-Python-OD统一考试(C卷)
题目描述: 输入字符串s,输出s中包含所有整数的最小和 说明 1. 字符串s,只包含 a-z A-Z +- ; 2. 合法的整数包括 1) 正整数 一个或者多个0-9组成,如 0 2 3 002 102 2)负整数 负号 - 开头,数字部分由一个或者多个0-9组成,如 -0 -012 -23 -00023 输入描述: 包含…...
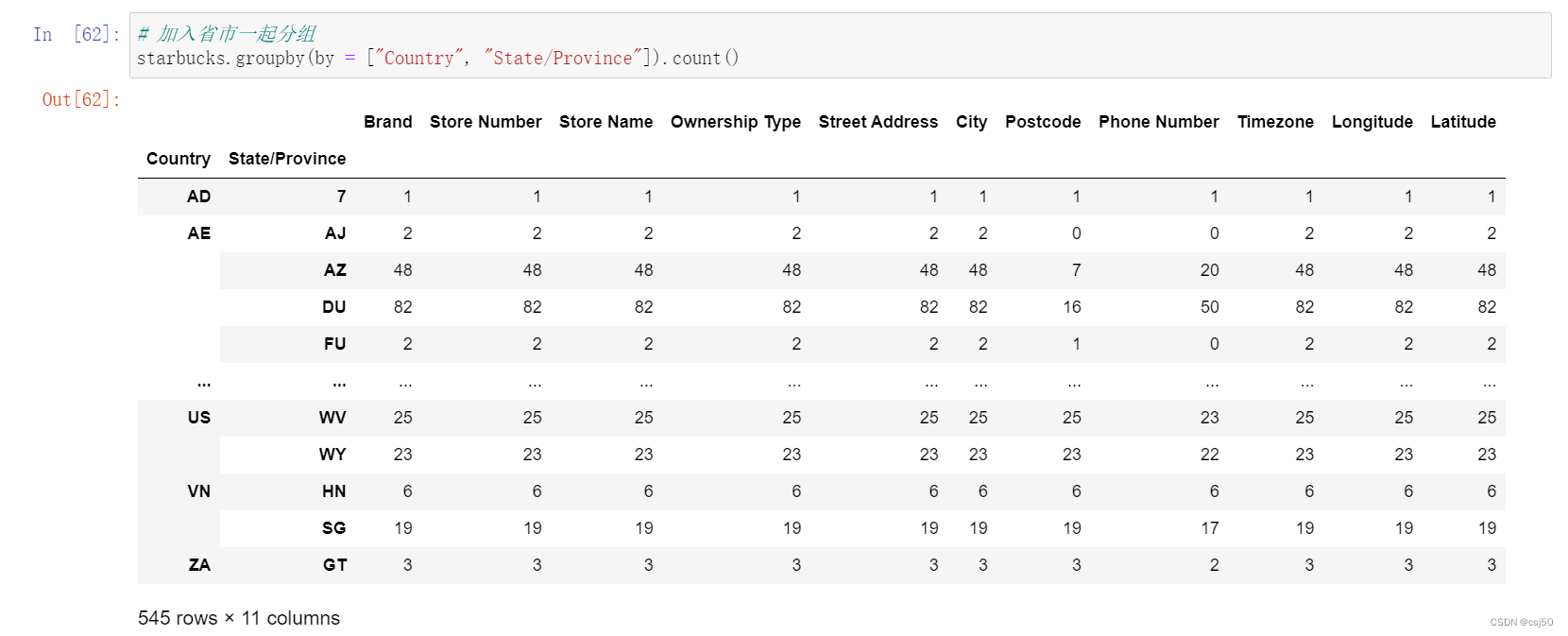
数据分析基础之《pandas(7)—高级处理2》
四、合并 如果数据由多张表组成,那么有时候需要将不同的内容合并在一起分析 1、先回忆下numpy中如何合并 水平拼接 np.hstack() 竖直拼接 np.vstack() 两个都能实现 np.concatenate((a, b), axis) 2、pd.concat([data1, data2], axis1) 按照行或者列…...

fluent脱硝SCR相对标准偏差、氨氮比、截面速度计算
# -*- coding: utf-8 -*- """ Created on Wed Sep 20 20:40:30 2023 联系QQ:3123575367,专业SCR脱硝仿真。 该程序用来处理fluent通过export-solution-ASCII-Space导出的数据,可计算标准偏差SD、相对标准偏差RSD,适用于求解平面的相对均匀…...
(A~E))
Codeforces Round 925 (Div. 3)(A~E)
题目暂时是AC,现在是Hack阶段,代码仅供参考。 A. Recovering a Small String 题目给出的n都可以由字母来组成,比如4可以是aab,字母里面排第一个和第二个,即1124。但是会歧义,比如aba为1214,也是…...

@RequestBody、@RequestParam、@RequestPart使用方式和使用场景
RequestBody和RequestParam和RequestPart使用方式和使用场景 1.RequestBody2.RequestParam3.RequestPart 1.RequestBody 使用此注解接收参数时,适用于请求体格式为 application/json,只能用对象接收 2.RequestParam 接收的参数是来自HTTP 请求体 或 请…...
LeetCode、1143. 最长公共子序列【中等,二维DP】
文章目录 前言LeetCode、1143. 最长公共子序列【中等,二维DP】题目链接与分类思路2022年暑假学习思路及题解二维DP解决 资料获取 前言 博主介绍:✌目前全网粉丝2W,csdn博客专家、Java领域优质创作者,博客之星、阿里云平台优质作者…...
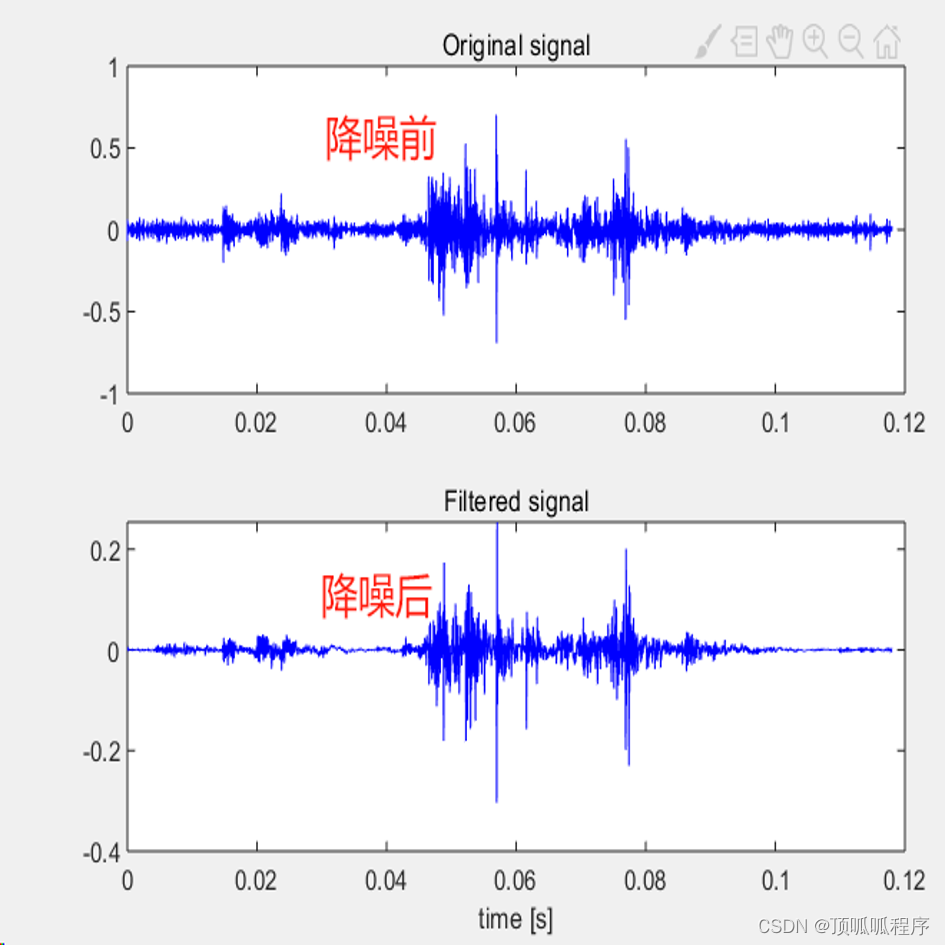
162基于matlab的多尺度和谱峭度算法对振动信号进行降噪处理
基于matlab的多尺度和谱峭度算法对振动信号进行降噪处理,选择信号峭度最大的频段进行滤波,输出多尺度谱峭度及降噪结果。程序已调通,可直接运行。 162 matlab 信号处理 多尺度谱峭度 (xiaohongshu.com)...

Android Studio六大基本布局的概览和每个布局的关键特性以及实例分析
1. 线性布局 (LinearLayout) 描述: 线性布局是一种按指定方向(水平或垂直)排列其子视图的布局容器。通过android:orientation属性可设置为horizontal或vertical。 关键属性: android:orientation: 指定布局方向。android:layout_weight: 子视图权重,用于分配剩余空间。示…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...


