随机过程及应用学习笔记(四) 马尔可夫过程
马尔可夫过程是理论上和实际应用中都十分重要的一类随机过程。
目录
前言
一、马尔可夫过程的概念
二、离散参数马氏链
1 定义
2 齐次马尔可夫链
3 齐次马尔可夫链的性质
三、齐次马尔可夫链状态的分类
四、有限马尔可夫链
五、状态的周期性
六、极限定理
七、生灭过程
总结
前言
经典力学中,在一给定时刻t的轨道,完全可以用在某时刻t0<t的状态确定,而不必知道t0前的状态。这一原则推广到遵从概率规律而不是决定性规律的体系,即当过程在t-t0时刻所处的状态已知的情况下,过程在时刻t(t>≥t0)所处的状态与过程在t-t0时刻之前的状态无关。这种已知“现在”的条件下,“将来”与“过去”无关的性质,就是直观意义下的马尔可夫性或称为无后效性。具有无后效性的过程称为马尔可夫过程。
一、马尔可夫过程的概念
一个马尔可夫过程由以下几个要素构成:
-
状态空间 (State Space): 表示可能的状态集合,记作 S。
-
转移概率 (Transition Probability): 描述从一个状态到另一个状态的概率。对于离散时间的情况,可以用转移矩阵 P 表示,其中 P(i, j) 表示从状态 i 转移到状态 j 的概率。数学上,这可以表示为:
P(Xn+1=j∣Xn=i)=Pij
其中Xn 表示在时刻 n 的状态,Pij 是从状态 i 转移到状态 j 的概率。
-
初始概率分布 (Initial Probability Distribution): 描述在初始时刻系统处于每个状态的概率分布。
马尔可夫过程可以分为离散时间马尔可夫链和连续时间马尔可夫过程两种。在连续时间的情况下,转移概率可以用转移率 (transition rate) 来描述


二、离散参数马氏链
1 定义
离散参数马氏链(Discrete-time Markov Chain)是一个随机过程,具有马尔可夫性质,而且在离散的时间步长内进行状态的转移。以下是离散参数马氏链的一般定义:
-
状态空间 (State Space): 表示系统可能处于的所有状态的集合,通常用 S 表示。
-
初始概率分布 (Initial Probability Distribution): 描述在初始时刻系统处于每个状态的概率分布,通常用 P(X0=i) 表示,其中 i 是状态空间中的一个状态。
-
转移概率 (Transition Probability): 描述在给定当前状态的情况下,系统转移到下一个状态的概率。用 Pij 表示从状态 i 转移到状态 j 的概率,其中 i,j∈S。转移概率矩阵 P 是一个矩阵,其元素为Pij。
转移概率满足以下性质: P(Xn+1=j∣Xn=i)=Pij
对于所有的 i,j∈S 和 n=0,1,2,…。
-
马尔可夫性 (Markov Property): 离散参数马氏链具有无后效性,即在给定当前状态的情况下,未来的状态只依赖于当前状态,而与过去的状态无关。


2 齐次马尔可夫链
齐次马尔可夫链(Homogeneous Markov Chain)是指在其转移概率在时间上保持不变的离散参数马尔可夫链。这意味着系统的状态转移概率在时间上是恒定的,不依赖于具体的时间步长。
具体来说,对于一个齐次马尔可夫链,转移概率 Pij 在不同的时间步长上是相同的。即对于所有的状态 i,j 和时间步长 n,都有:
P(Xn+1=j∣Xn=i)=Pij
其中Pij 是常数,矩阵 P 中的元素。这表示齐次马尔可夫链的转移概率矩阵在时间上保持不变。
齐次马尔可夫链的特性使得我们可以更容易地分析系统的稳定性和长期行为。通过对转移概率矩阵的特征值和特征向量进行分析,可以得到关于系统长期行为的信息,例如平稳分布等。
3 齐次马尔可夫链的性质
齐次马尔可夫链(Homogeneous Markov Chain)具有一些重要的性质,这些性质有助于我们理解和分析系统在长期演变中的行为。以下是齐次马尔可夫链的一些主要性质:
-
稳定分布(Stationary Distribution): 如果齐次马尔可夫链具有有限的状态空间且是不可约的(即从任一状态可以到达任一其他状态),则存在一个唯一的稳定分布。该稳定分布是一个概率分布,表示在长时间内系统处于各个状态的概率。稳定分布可以通过解 πP=π 的方程得到,其中 π 是稳定分布向量,P 是转移概率矩阵。
-
周期性(Periodicity): 齐次马尔可夫链可能具有周期性,即存在一个正整数 d,使得从某一状态出发,返回该状态的最小步数是 d 的倍数。如果 d=1,则称该状态是非周期的;否则,称为周期为 d。
-
吸收态(Absorbing States): 一些状态可能是吸收态,即从这些状态出发,不可能离开。一旦达到吸收态,系统将永远留在这些状态上。
-
遍历性(Recurrence): 齐次马尔可夫链中的状态可以分为遍历态和非遍历态。如果从某一状态出发,最终回到该状态的概率为1,则称该状态是遍历态;否则,称为非遍历态。
-
极限分布(Limiting Distribution): 如果齐次马尔可夫链是不可约的且非周期的,那么它在长时间内会趋向于一个极限分布。这意味着随着时间的推移,系统的状态分布将收敛到一个稳定的概率分布。
三、齐次马尔可夫链状态的分类
在齐次马尔可夫链中,状态可以被分类为以下几类:
-
遍历态(Recurrent States): 一个状态是遍历态,如果从该状态出发,经过一定的时间步骤后,有概率1回到该状态。遍历态可以进一步分为正常遍历态和零遍历态:
- 正常遍历态(Positive Recurrent States):如果期望回到该状态的时间是有限的,即 E(Ti∣X0=i)<∞,其中 Ti 是回到状态 i 所需的步数。
- 零遍历态(Null Recurrent States):如果期望回到该状态的时间是无限的,即 E(Ti∣X0=i)=∞。
-
非遍历态(Transient States): 一个状态是非遍历态,如果从该状态出发,经过一定的时间步骤后,有概率0回到该状态。非遍历态是一种一次性的状态,一旦离开就不再返回。
-
吸收态(Absorbing States): 一个状态是吸收态,如果从该状态出发,无论经过多少步骤,都不可能离开。吸收态是一种特殊的遍历态。
-
周期性(Periodic States): 一个状态可能是周期性的,即存在一个正整数 d,使得从该状态出发,返回该状态的最小步数是 d 的倍数。如果d=1,则称该状态是非周期的。






四、有限马尔可夫链

五、状态的周期性
在马尔可夫链中,状态的周期性描述了从某个状态出发,返回该状态的步数的性质。一个状态的周期性被定义为该状态上的最小正整数 d,使得从该状态出发返回的步数都是 d 的倍数。
形式化地,对于状态 i,其周期 di 定义如下:
di=gcd{n>0:P(Xn=i∣X0=i)>0}
其中 gcdgcd 表示最大公约数。如果di=1,则状态 i 是非周期的;否则,它是周期为 di 的周期性状态。
状态的周期性有一些重要的性质:
-
周期状态的集合: 马尔可夫链的状态可以分为不同的周期性类别,每个类别包含具有相同周期的状态。这使得我们可以将状态空间分解为周期性类别,从而更好地理解系统的结构。
-
周期性状态的影响: 对于非周期状态,长期行为通常更容易分析,因为系统在这些状态间随着时间的推移更加均匀。然而,周期性状态可能导致系统的行为变得更为复杂,因为它涉及到周期性的振荡。
-
周期性状态的影响: 在周期性状态的情况下,系统可能在某些时间步长内呈现出规律性的变化,而在另一些时间步长内可能呈现出较为静态的状态。
六、极限定理
两个与马尔可夫过程相关的极限定理是大数定律和中心极限定理。
-
大数定律(Law of Large Numbers): 大数定律对于随机过程的极限定理描述了随机变量序列的均值在样本容量趋于无穷时的稳定性。对于马尔可夫过程,大数定律可以表示为,在长时间内,马尔可夫过程的状态分布趋于稳定。这意味着在马尔可夫链中,随着时间的推移,系统的状态分布趋于某个稳定的分布。
-
中心极限定理(Central Limit Theorem): 中心极限定理是另一个重要的极限定理,它描述了随机变量序列的和或均值在样本容量趋于无穷时的分布。对于马尔可夫过程,中心极限定理可以用来描述在一些条件下,随机过程的和或均值的分布在适当的标准化下趋于正态分布。这个定理对于理解马尔可夫过程的渐近性质非常有帮助。
七、生灭过程
生灭过程(Birth-and-Death Process)是马尔可夫过程的一种,其中系统中的状态可以通过出生和死亡两种基本的随机事件进行转移。这类过程通常用于模拟描述人口、分子数、队列长度等随时间变化的数量。
生灭过程的特点包括:
-
有限状态空间: 生灭过程通常涉及有限个状态。这些状态通常按照一定的顺序排列,形成状态链。
-
状态转移: 在生灭过程中,状态之间的转移只能通过出生(birth)和死亡(death)两种基本事件进行。出生事件导致系统的状态增加,而死亡事件导致状态减少。
-
状态转移概率: 生灭过程的状态转移概率取决于当前状态,即转移到下一个状态的概率仅与当前状态有关。
-
无向图表示: 通常可以使用无向图来表示生灭过程,其中每个状态对应一个节点,而状态之间的转移由边表示。边上的权重表示从一个状态转移到另一个状态的概率。
数学上,生灭过程的特点可以用转移概率来描述。设 Pi,i+1 表示从状态 i 转移到状态 i+1 的概率,而 Pi,i−1 表示从状态 i 转移到状态 i−1 的概率。则生灭过程的转移概率可以表示为:
P(Xn+1=i+1∣Xn=i)=Pi,i+1
P(Xn+1=i−1∣Xn=i)=Pi,i−1
P(Xn+1=i∣Xn=i)=1−Pi,i+1−Pi,i−1
生灭过程的分析涉及到马尔可夫链的理论和技巧,可以通过平衡方程、极限定理等方法来研究其性质。
总结
马尔可夫过程在数学、物理、生物学、经济学和工程学等各个领域都有广泛的应用。
相关文章:

随机过程及应用学习笔记(四) 马尔可夫过程
马尔可夫过程是理论上和实际应用中都十分重要的一类随机过程。 目录 前言 一、马尔可夫过程的概念 二、离散参数马氏链 1 定义 2 齐次马尔可夫链 3 齐次马尔可夫链的性质 三、齐次马尔可夫链状态的分类 四、有限马尔可夫链 五、状态的周期性 六、极限定理 七、生灭过…...

prometheus
文章目录 一、Prometheus简介什么是Prometheus?Prometheus的优势Prometheus的组件、架构Prometheus适用于什么场景Prometheus不适合什么场景 二、相关概念数据模型指标名称和标签样本表示方式 指标类型Counter计数器Gauge仪表盘Histogram直方图Summary摘要 Jobs和In…...
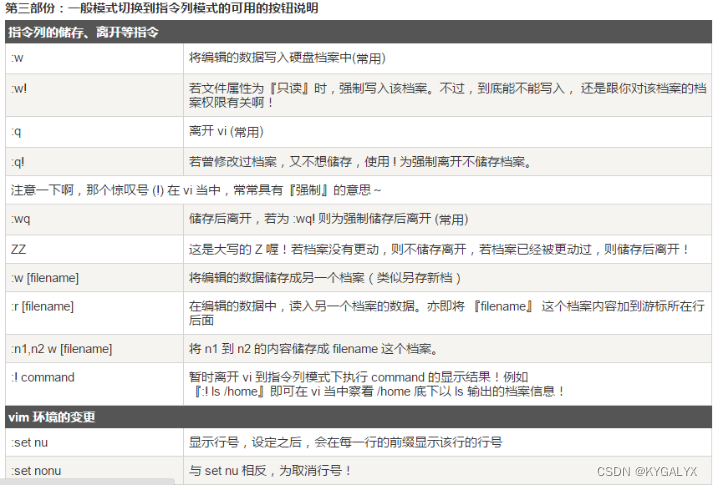
Vi 和 Vim 编辑器
Vi 和 Vim 编辑器 vi 和 vim 的基本介绍 Linux 系统会内置 vi 文本编辑器 Vim 具有程序编辑的能力,可以看做是 Vi 的增强版本,可以主动的以字体颜色辨别语法的正确性,方便程序设计。 代码补完、编译及错误跳转等方便编程的功能特别丰富&…...
算法沉淀——队列+宽度优先搜索(BFS)(leetcode真题剖析)
算法沉淀——队列宽度优先搜索(BFS) 01.N 叉树的层序遍历02.二叉树的锯齿形层序遍历03.二叉树最大宽度04.在每个树行中找最大值 队列 宽度优先搜索算法(Queue BFS)是一种常用于图的遍历的算法,特别适用于求解最短路径…...
编辑器的新选择(基本不用配置)
Cline 不用看网上那些教程Cline几乎不用配置。 点击设置直接选择Chinese, C直接在选择就行了。 Cline是一个很好的编辑器,有很多懒人必备的功能。 Lightly 这是一个根本不用配置的C编辑器。 旁边有目录,而且配色也很好,语言标准可以自己…...

算法沉淀——栈(leetcode真题剖析)
算法沉淀——栈 01.删除字符串中的所有相邻重复项02.比较含退格的字符串03.基本计算器 II04.字符串解码05.验证栈序列 栈(Stack)是一种基于先进后出(Last In, First Out,LIFO)原则的数据结构。栈具有两个主要的操作&am…...

耳机壳UV树脂制作私模定制耳塞需要注意什么问题?
制作私模定制耳塞需要注意以下问题: 耳模制作:获取准确的耳模是制作私模定制耳塞的关键步骤。需要使用合适的材料和方法,确保耳模的准确性和稳定性。材料选择:选择合适的UV树脂和其它相关材料,确保它们的质量和性能符…...

easyx搭建项目-永七大作战(割草游戏)
永七大作战 游戏介绍: 永七大作战 游戏代码链接:永七大作战 提取码:ABCD 不想水文了,直接献出源码,表示我的诚意...

nginx命名location跳转的模块上下文继承
目录 1. 缘起2. 解决方案2.1 保留指定模块的上下文信息2.2 获取指定模块的上下文信息2.3 设置指定模块的上下文信息2.4 设置模块上下文是否需要继承标记2.5 对openrety lua代码的支持 1. 缘起 nginx提供了非常棒的功能,命名location,如文章nginx的locati…...
)
洛谷 P2678 [NOIP2015 提高组] 跳石头 (Java)
洛谷 P2678 [NOIP2015 提高组] 跳石头 (Java) 传送门:P2678 [NOIP2015 提高组] 跳石头 题目: [NOIP2015 提高组] 跳石头 题目背景 NOIP2015 Day2T1 题目描述 一年一度的“跳石头”比赛又要开始了! 这项比赛将在一条笔直的河道中进行&…...
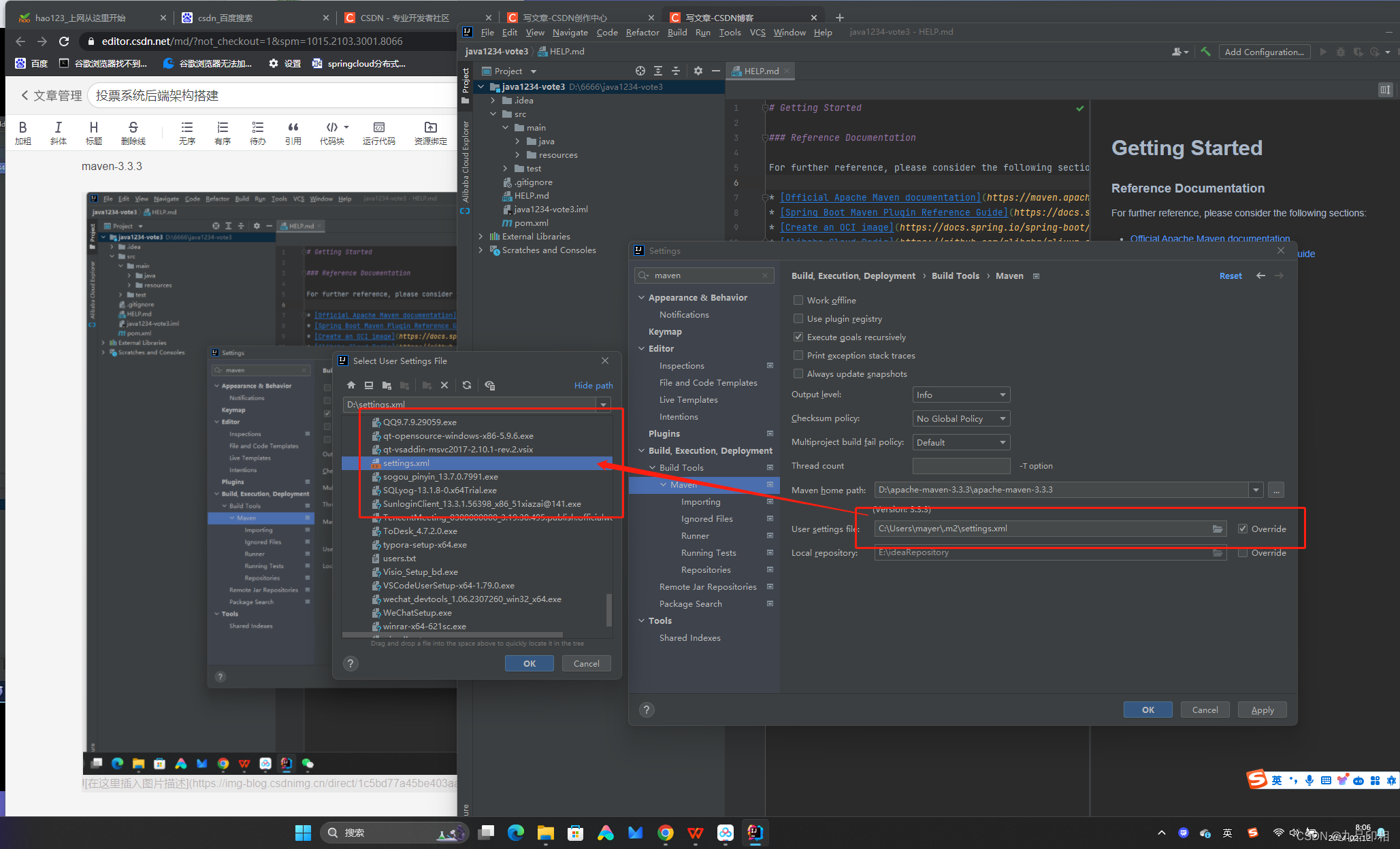
第2讲投票系统后端架构搭建
创建项目时,随机选择一个,后面会生成配置properties文件 生成文件 maven-3.3.3 设置阿里云镜像 <?xml version"1.0" encoding"UTF-8"?><!-- Licensed to the Apache Software Foundation (ASF) under one or more cont…...
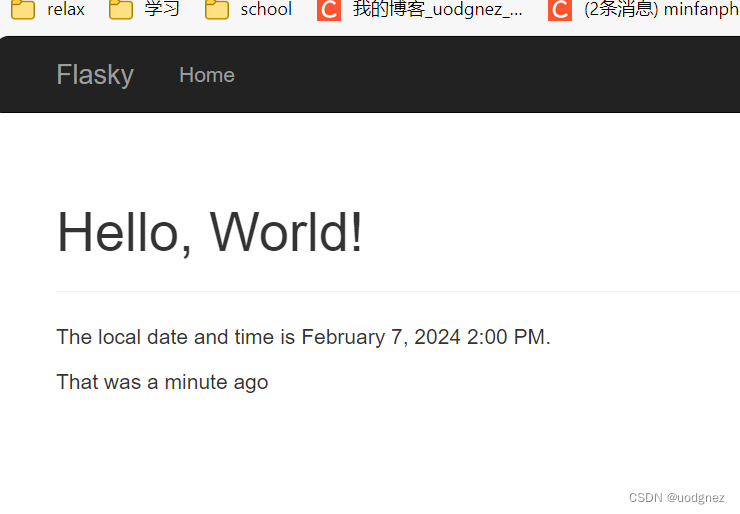
Flask 入门7:使用 Flask-Moment 本地化日期和时间
如果Web应用的用户来自世界各地,那么处理日期和时间可不是一个简单的任务。服务器需要统一时间单位,这和用户所在的地理位置无关,所以一般使用协调世界时(UTC)。不过用户看到 UTC 格式的时间会感到困惑,他们…...

FileZilla Server 1.8.1内网搭建
配置环境服务器服务器下载服务器配置服务器配置 Server - ConfigureServer Listeners - Port 协议设置 Protocols settingsFTP and FTP over TLS(FTPS) Rights management(权利管理)Users(用户) 客户端建立连接 配置环境 服务器处于局域网内: 客户端 < -访问- > 公网 &l…...
C++LNK1207中的 PDB 格式不兼容;请删除并重新生成
在打开别人发的C文件时,可能出现该报错 解决办法 打开资源管理器,找到原来的路径 进入Debug, 找到对应的PDB文件删除即可。...

小白学习Halcon100例:如何利用动态阈值分割图像进行PCB印刷缺陷检测?
文章目录 *读入图片*关闭所有窗口*获取图片尺寸*根据图片尺寸打开一个窗口*在窗口中显示图片* 缺陷检测开始 ...*1.开运算 使用选定的遮罩执行灰度值开运算。*2.闭运算 使用选定的遮罩执行灰度值关闭运算*3.动态阈值分割 使用局部阈值分割图像显示结果*显示原图*设置颜色为红色…...
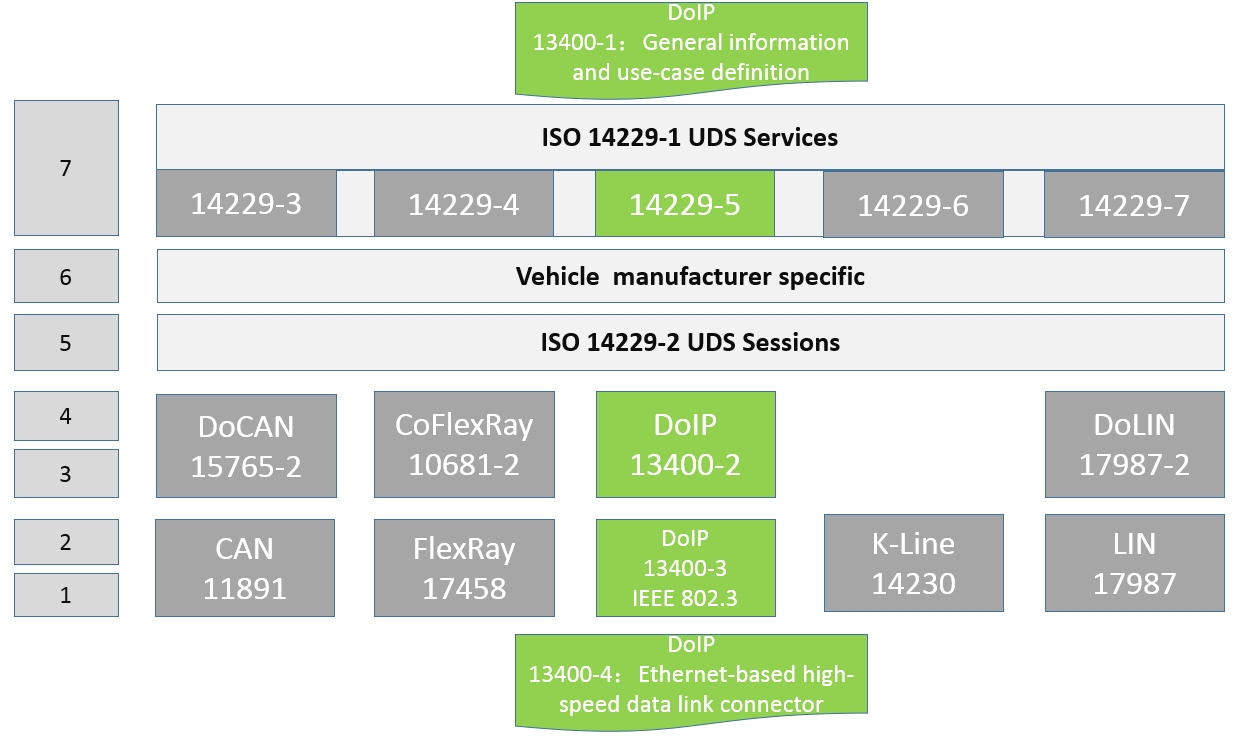
车载诊断协议DoIP系列 —— 车载以太网诊断需求规范(网关、路由)
车载诊断协议DoIP系列 —— 车载以太网诊断需求规范(网关、路由) 我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师(Wechat:gongkenan2013)。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 本就是小人物,输了就是输了,不要在意别人怎么看自…...

面试官:介绍一下MVC框架
前言 大家好,我是chowley,MVC相信大家都听说过,今天我就记录一下我心中的MVC框架 MVC(Model-View-Controller)是一种软件设计模式,用于将应用程序分为三个核心部分:模型(Model&…...

C++ new 和 malloc 的区别?
相关系列文章 C内存分配策略-CSDN博客 目录 1.引言 2.区别 2.1.申请的内存分配区域 2.2.类型安全和自动大小计算 2.3.构造函数和析构函数的调用 2.4.异常处理 2.5.配对简便性 2.6.new 的重载 2.7.关键字和操作符 3.总结 1.引言 new 和 delete 在 C 中被引入…...
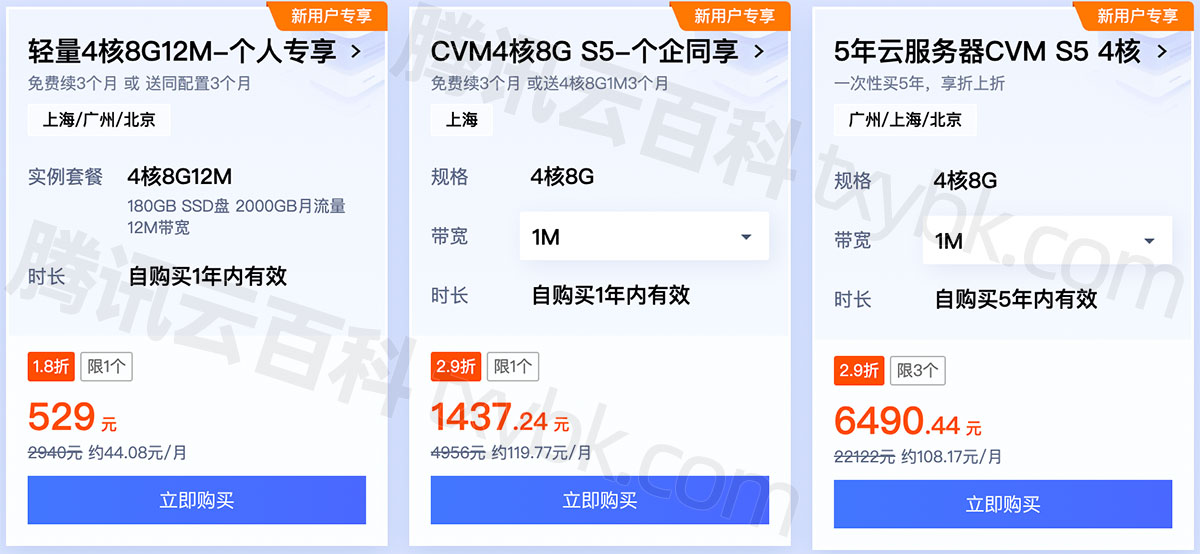
腾讯云4核8G服务器多少钱?
腾讯云4核8G服务器多少钱?轻量应用服务器4核8G12M带宽一年446元、646元15个月,云服务器CVM标准型S5实例4核8G配置价格15个月1437.3元,5年6490.44元,标准型SA2服务器1444.8元一年,在txy.wiki可以查询详细配置和精准报价…...

独孤思维:看到副业坚持4年,我震惊了
01 新人写作,不要写纯理论的东西,也不要写自我高潮的内容。 都写点接地气,多实操的内容。 比如,独孤现在每一篇短文写作,都会引入一个案例。 这样,对于很多读者来说,更好理解,能…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
