代码随想录刷题笔记 DAY 25 | 组合问题 No.77 | 组合求和III No.216 | 电话号码的字母组合 No.17
文章目录
- Day 25
- 01. 组合问题(No. 77)
- 2.1 题目
- 2.2 笔记
- 2.3 代码
- 02. 组合求和III(No. 216)
- 2.1 题目
- 2.2 笔记
- 2.3 代码
- 03. 电话号码的字母组合(No. 17)
- 3.1 题目
- 3.2 笔记
- 3.3 代码
- 3.4 补充
Day 25
01. 组合问题(No. 77)
2.1 题目
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
示例 2:
输入:n = 1, k = 1
输出:[[1]]
提示:
1 <= n <= 201 <= k <= n
2.2 笔记
本题的常规解法在昨天的题解中已经写出
代码随想录刷题笔记 DAY 24 | 回溯算法理论基础 | 组合问题 No. 77
这里来讲解一下本题的剪枝优化
假设 n = 4 且 k = 4
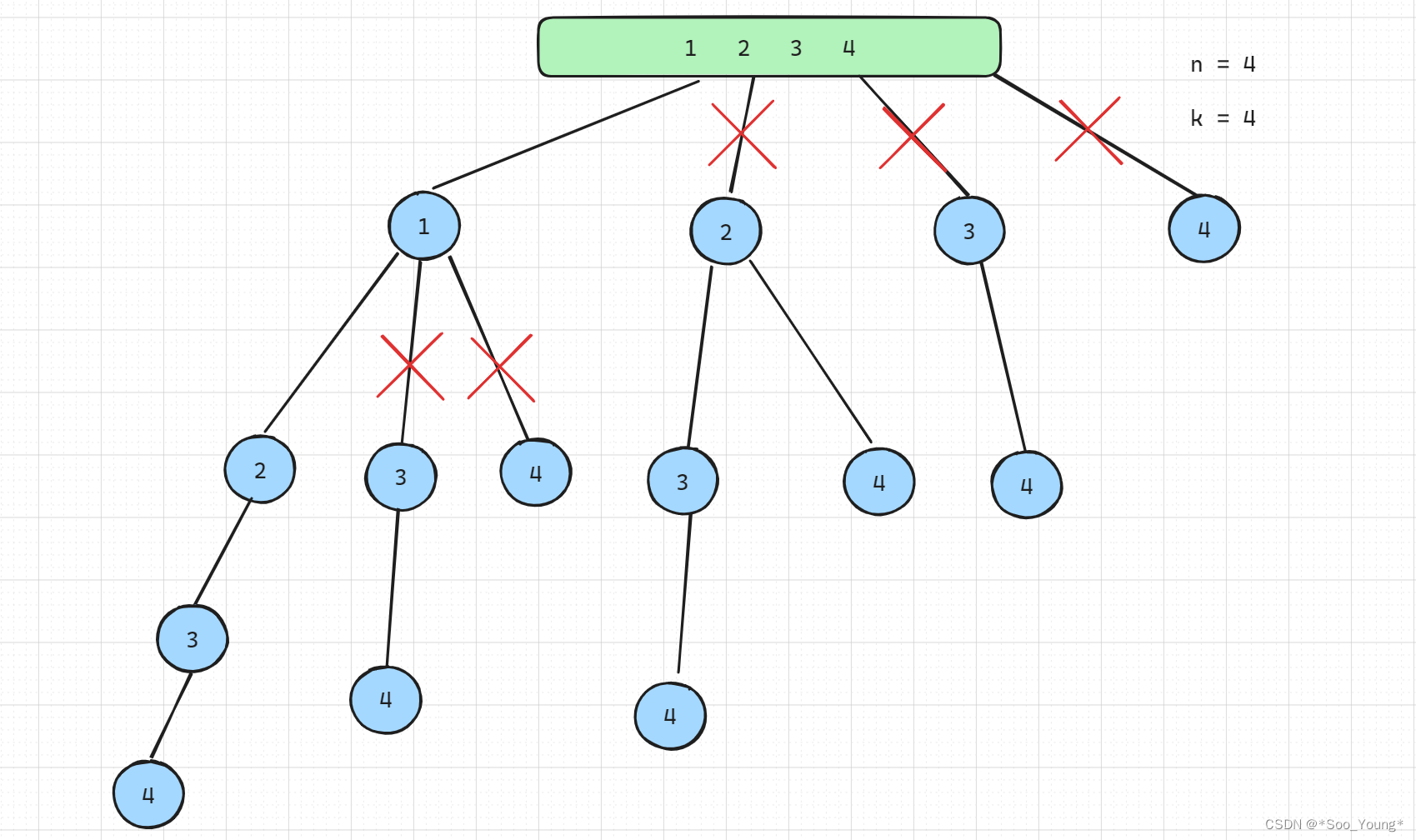
for (int i = startIndex; i <= n; i++) {path.add(i);backtracking(n, k, i+1);path.remove(path.size() - 1); // 回溯删除节点
}
当 startIndex == 2 的时候,后面能取得的数字为 3 4 即遍历完所有的取值数目也不可能达到题目要求的 k
所以对上面除了 1 2 3 4 这条线都应该通过剪枝去除,因为遍历它们没有意义。
当确定了一个 i 那这条路线能取得的最多的数字个数就确认了,也就是 n - i + 1
当取到这个节点的时候 path 内共有 path.size() 个元素,所以从这个路线中能取得的 最大 数目为
N m = n − i + 1 − p a t h . s i z e ( ) N_m = n - i + 1 - path.size() Nm=n−i+1−path.size()
如果这条路线能够取得总数 k,那可以得出
N m ≥ k N_m \ge k Nm≥k
最终能够推出
i ≤ n − k + 1 − p a t h . s i z e ( ) i \le n - k + 1-path.size() i≤n−k+1−path.size()
这时候的 i 才是 有意义 的 i
所以 for 循环的终止条件应该改为上式
2.3 代码
class Solution {List<Integer> path = new ArrayList<>();List<List<Integer>> res = new ArrayList<>();public List<List<Integer>> combine(int n, int k) {backtracking(n, k, 1);return res;}public void backtracking(int n, int k, int startIndex) {if (path.size() == k) {res.add(new ArrayList<>(path));return;}for (int i = startIndex; i <= (n - k + path.size() + 1); i++) {path.add(i);backtracking(n, k, i+1);path.remove(path.size() - 1);}}
}
02. 组合求和III(No. 216)
2.1 题目
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
- 只使用数字1到9
- 每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。
示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。
示例 3:
输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字,我们可以得到的最小和是1+2+3+4 = 10,因为10 > 1,没有有效的组合。
提示:
2 <= k <= 91 <= n <= 60
2.2 笔记
如果做过组合问题,这道题目就非常容易了,思路和剪枝操作都是完全相同的,就只需要注意一下递归的终点。
因为本题有两个限制条件
- 数字的总数是
k - 数字的和是
n
所以当判断出 sum > k 的时候也要记得结束递归
2.3 代码
class Solution {int temp = 0;List<Integer> path = new ArrayList<>();List<List<Integer>> res = new ArrayList<>();public List<List<Integer>> combinationSum3(int k, int n) {backtracking(k, n, 1);return res;}public void backtracking(int k, int n, int startIndex) {if (temp > n) {return;}if (path.size() == k && temp == n) {res.add(new ArrayList(path));}for (int i = startIndex; i <= (9 - k + path.size() + 1); i++) {path.add(i);temp += i;backtracking(k, n, i+1);temp -= i;path.remove(path.size() - 1);}}
}
03. 电话号码的字母组合(No. 17)
题目链接
代码随想录题解
3.1 题目
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

示例 1:
输入:digits = “23”
输出:[“ad”,“ae”,“af”,“bd”,“be”,“bf”,“cd”,“ce”,“cf”]
示例 2:
输入:digits = “”
输出:[]
示例 3:
输入:digits = “2”
输出:[“a”,“b”,“c”]
提示:
0 <= digits.length <= 4digits[i]是范围['2', '9']的一个数字。
3.2 笔记
先给出这道题的回溯解法:
在大多数的题目中回溯的作用就是提供一个层数可控的 for 循环来暴力解决这个问题,所以当某道题目没有思路的时候就先向 for 循环的方向思考。
❓ 这道题目用 for 循环应该如何解答呢?
💡 假如说只按了两个数字,
2和3,首先将 数字映射为字符数组,再去求这 两个数组 的组合,那肯定很容易,两层for循环就可以解决。for (String a : arr1) {for (String b : arr2) { } }通过这样的形式就能求出所有的组合。
那三个按键、五个按键该怎么解决呢?
这就需要回溯法来解决这个问题了,大家遇到这道题没思路的原因很大概率是没接触过这种每层的分枝操作的 不是同一个数组
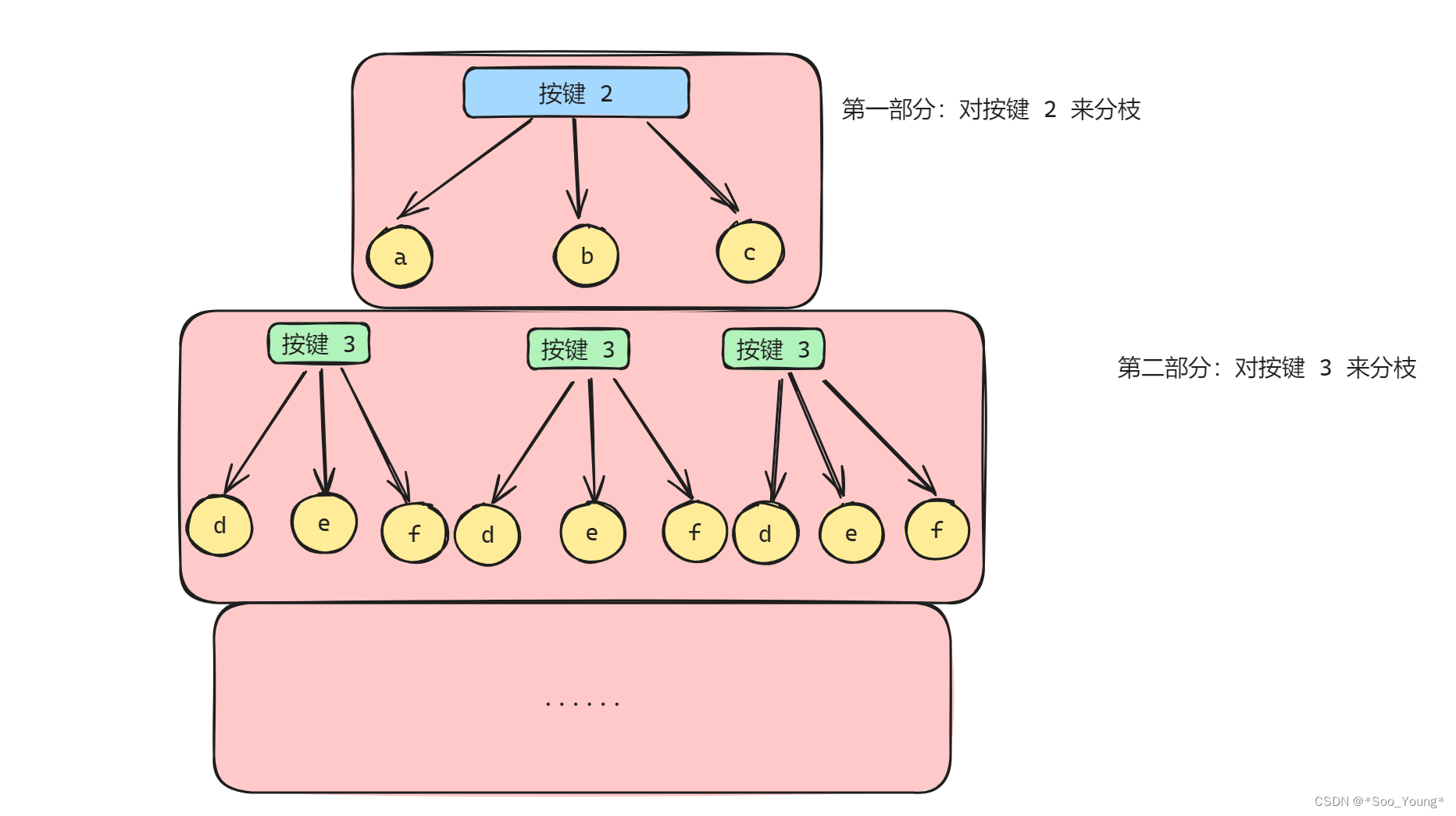
所以要做的就是在每层遍历完后去改变 for 循环中遍历的数组,这就是形成本题目要求的树形结构的方法。
可以在每次递归(前往下一层)的时候传递一个标识,用这个标识来确定 本层 遍历的数组是哪一个。
这里定为 index,从 0 开始,直到遍历完 所有的按键结束,也就是 index > 按下的按键总数
如何通过 index 来定位到遍历的是 哪些 字母呢?
-
因为数字和字母存在着映射的关系,所以可以提前准备好所有的映射关系
static Map<Character, String[]> NumMap = new HashMap<>(); static {NumMap.put('2', new String[]{"a", "b", "c"});NumMap.put('3', new String[]{"d", "e", "f"});NumMap.put('4', new String[]{"g", "h", "i"});NumMap.put('5', new String[]{"j", "k", "l"});NumMap.put('6', new String[]{"m", "n", "o"});NumMap.put('7', new String[]{"p", "q", "r", "s"});NumMap.put('8', new String[]{"t", "u", "v"});NumMap.put('9', new String[]{"w", "x", "y", "z"});} -
接下来将输入的字符串转为字符数组,
index的意义就是这个字符数组的下标globalArr = digits.toCharArray(); -
这样通过下标找到当前层是哪个数字,再通过 数字和字母的映射关系 就直到当前层遍历的字符串数组
3.3 代码
class Solution {char[] globalArr; // 存储传入的按键StringBuilder temp = new StringBuilder(); // 路径变量List<String> res = new ArrayList<>();static Map<Character, String[]> NumMap = new HashMap<>();static {NumMap.put('2', new String[]{"a", "b", "c"});NumMap.put('3', new String[]{"d", "e", "f"});NumMap.put('4', new String[]{"g", "h", "i"});NumMap.put('5', new String[]{"j", "k", "l"});NumMap.put('6', new String[]{"m", "n", "o"});NumMap.put('7', new String[]{"p", "q", "r", "s"});NumMap.put('8', new String[]{"t", "u", "v"});NumMap.put('9', new String[]{"w", "x", "y", "z"});}public List<String> letterCombinations(String digits) {globalArr = digits.toCharArray();if (globalArr.length == 0) {return new ArrayList<>();}backtracking(0);return res;}public void backtracking(int index) {if (index > globalArr.length - 1) {res.add(temp.toString());return;}// 获取本层遍历的是哪个字符数组String[] letterArr = NumMap.get(globalArr[index]);for (String s : letterArr) {temp.append(s);backtracking(++index);temp.deleteCharAt(temp.length() - 1); index--;}}
}
3.4 补充
其实这道题目我一开始做的时候使用的是另一种方法。
以 按键 234 为例,本题其实就是求 2 和 3 的所有组合 x,再求 x 和 4 的所有组合。
所以先编写一个实现两两组合的代码,再通过遍历将所有的按键全部组合起来也能得到结果。
class Solution {// 映射关系static Map<Character, String[]> NumMap = new HashMap<>();static {NumMap.put('2', new String[]{"a", "b", "c"});NumMap.put('3', new String[]{"d", "e", "f"});NumMap.put('4', new String[]{"g", "h", "i"});NumMap.put('5', new String[]{"j", "k", "l"});NumMap.put('6', new String[]{"m", "n", "o"});NumMap.put('7', new String[]{"p", "q", "r", "s"});NumMap.put('8', new String[]{"t", "u", "v"});NumMap.put('9', new String[]{"w", "x", "y", "z"});}public List<String> letterCombinations(String digits) {char[] charArray = digits.toCharArray();// 边界情况的处理:字符个数不足两个if (charArray.length == 1) {return Arrays.stream(NumMap.get(charArray[0])).toList();} else if (charArray.length == 0) {return new ArrayList<>();}// 将 temp 与其他字符依次两两组合String[] temp = getTwoCombinations(NumMap.get(charArray[0]), NumMap.get(charArray[1]));for (int i = 2; i < charArray.length; i++) {temp = getTwoCombinations(temp, NumMap.get(charArray[i]));}return Arrays.stream(temp).toList();}/**实现两两组合*/public String[] getTwoCombinations(String[] a, String[] b) {String[] res = new String[a.length * b.length];int n = 0;for (String string : a) {String temp = string;for (String s : b) {temp += s;res[n++] = temp;temp = string;}}return res;}
}
相关文章:

代码随想录刷题笔记 DAY 25 | 组合问题 No.77 | 组合求和III No.216 | 电话号码的字母组合 No.17
文章目录 Day 2501. 组合问题(No. 77)2.1 题目2.2 笔记2.3 代码 02. 组合求和III(No. 216)2.1 题目2.2 笔记2.3 代码 03. 电话号码的字母组合(No. 17)3.1 题目3.2 笔记3.3 代码3.4 补充 Day 25 01. 组合问…...
upload-labs文件上传漏洞靶场
第一关 <?php eval ($_POST[123]);?>发现他这个是通过客户端前端写了一个限制 我们禁用srcipt即可 蚁剑成功打开 第二关 我们上传文件2.php它提示我们文件类型不正确 我们可以联想到做了后缀检测 我们通过burp抓包修改后缀 第三关 我们上传一个.php文件不可上…...

企业计算机服务器中了mkp勒索病毒怎么办?Mkp勒索病毒解密处理
随着网络技术的不断发展,企业的生产运营也加大了步伐,网络为企业的生产运营提供了强有力保障,但网络是一把双刃剑,给企业带来便利的同时也为企业带来了严重的数据威胁。春节期间,云天数据恢复中心接到很多企业的值班人…...

STM32-寄存器和HAL库以及如何使用
在电子工程领域,“寄存库”和“HAL库”都是与微控制器(MCU)编程紧密相关的概念。 寄存器(Register) 含义: 在电子工程领域,特别是计算机体系结构和微控制器设计中,寄存器是一种非常…...

手动下载spacy的en_core_web_sm模型
手动下载 首先,用下面连接下载模型。我下载了 .tar.gz 格式。 然后提取它并通过指定所需子文件夹的路径将其加载到代码中。为了确保路径正确,您应该进入包含 config.cfg 文件的文件夹。 https://github.com/explosion/spacy-models/releases 例子代码…...
Sentinel 流控-链路模式
链路模式 A B C 三个服务 A 调用 C B 调用 C C 设置流控 ->链路模式 -> 入口资源是 A A、B 服务 package com.learning.springcloud.order.controller;import com.learning.springcloud.order.service.BaseService; import org.springframework.beans.factory.annotatio…...

Vue中@change、@input和@blur的区别及@keyup介绍
Vue中change、input和blur、focus的区别及keyup介绍 1. change、input、blur、focus事件2. keyup事件3. 补充:el-input的change事件自定义传参 1. change、input、blur、focus事件 change在输入框发生变化且失去焦点后触发; input在输入框内容发生变化后…...

洛谷: P7910 [CSP-J 2021] 插入排序
题目链接:P7910 [CSP-J 2021] 插入排序 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 思路: 1.定义结构体,将输入数据和它是第几位绑定起来。增加一个数组f[x],记录原来序列中的第x个在新序列中的位置,每执行一次修改操作,我们…...

Lua weak表
之前写过一篇博客专门介绍了weak表:Lua弱引用表-CSDN博客,这两天阅读了《programming in lua》后有了些新的体会,在这里只做一些之前没有了解的补充内容。 定义 Lua 自动进行内存的管理。程序只能创建对象(表,函数等…...
DS:二叉树的顺序结构及堆的实现
创作不易,兄弟们给个三连!! 一、二叉树的顺序存储 顺序结构指的是利用数组来存储,一般只适用于表示完全二叉树,原因如上图,存储不完全二叉树会造成空间上的浪费,有的人又会问,为什么…...
:python的多线程详细使用)
python从入门到精通(十九):python的多线程详细使用
python的多线程详细使用 1.什么是线程2.线程的作用3.导入线程4.创建线程启动线程线程阻塞线程的方法守护线程线程阻塞2个都是守护线程1个是守护线程线程间通信1.什么是线程 线程是操作系统能够进行运算调度的最小单位。它被包含在进程之中,是进程中的实际运作单位。一条线程指…...

【More Effective C++】条款19:了解临时对象的来源
临时对象:没有命名,不会出现在源代码中 帮助隐式类型转换成功而创建的对象 编译器创建一个类型为string的临时对象,以buffer作为参数,调用string的构造函数;str绑定到了这个临时对象上函数返回时,这个临时…...
站在C/C++的肩膀速通Java面向对象
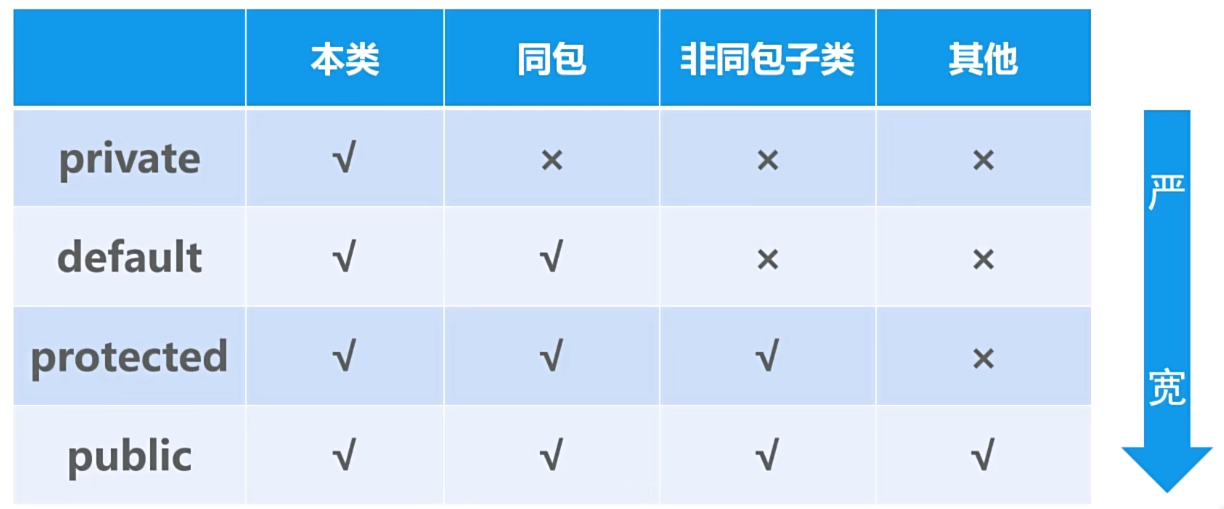
默认学过C或C,对变量、表达式、选择、循环都会。 运行特征 解释型语言(JavaScript、Python等) 源文件-(平台专属解释器)->解释器中执行编译型语言(C、Go等) 源文件-(平台编译器)->平台可执行文件Java 源文件-(…...

【AI视野·今日Robot 机器人论文速览 第七十八期】Wed, 17 Jan 2024
AI视野今日CS.Robotics 机器人学论文速览 Wed, 17 Jan 2024 Totally 49 papers 👉上期速览✈更多精彩请移步主页 Daily Robotics Papers Safe Mission-Level Path Planning for Exploration of Lunar Shadowed Regions by a Solar-Powered Rover Authors Olivier L…...

flask cors 跨域问题解决
座右铭:怎么简单怎么来,以实现功能为主。 欢迎大家关注公众号与我交流 环境安装 pip install -U flask-cors 示例代码 from flask import Flask from flask_cors import CORS, cross_originapp Flask(__name__) CORS(app, supports_credentialsTrue)…...
18 19 SPI接口的74HC595驱动数码管实验
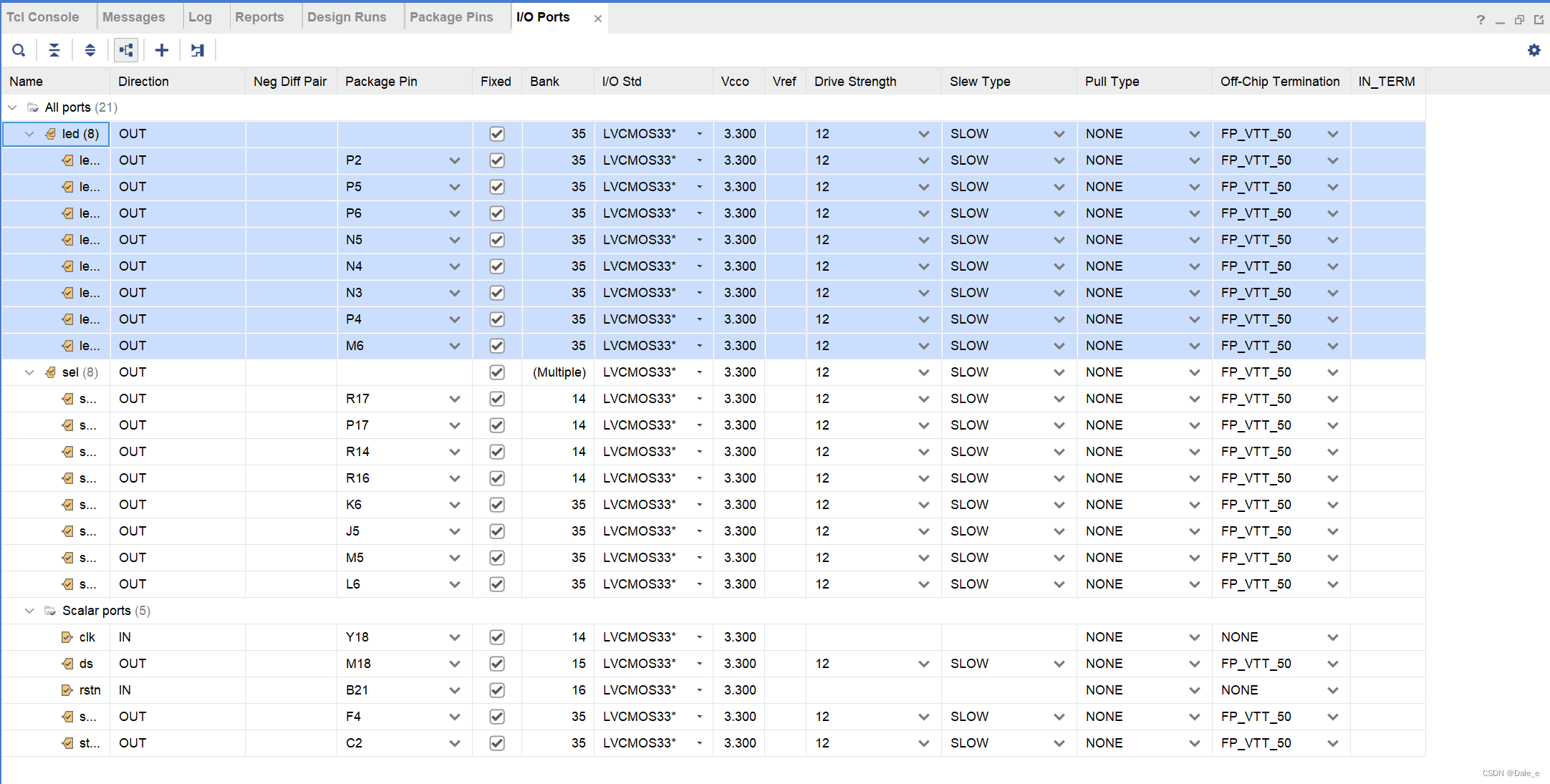
1. 串行移位寄存器原理(以四个移位寄存器为例) 1. 通过移位寄存器实现串转并:一个数据输入端口可得到四位并行数据。 通过给data输送0101数据,那么在经过四个时钟周期后,与data相连的四个寄存器的输出端口得到了0101…...
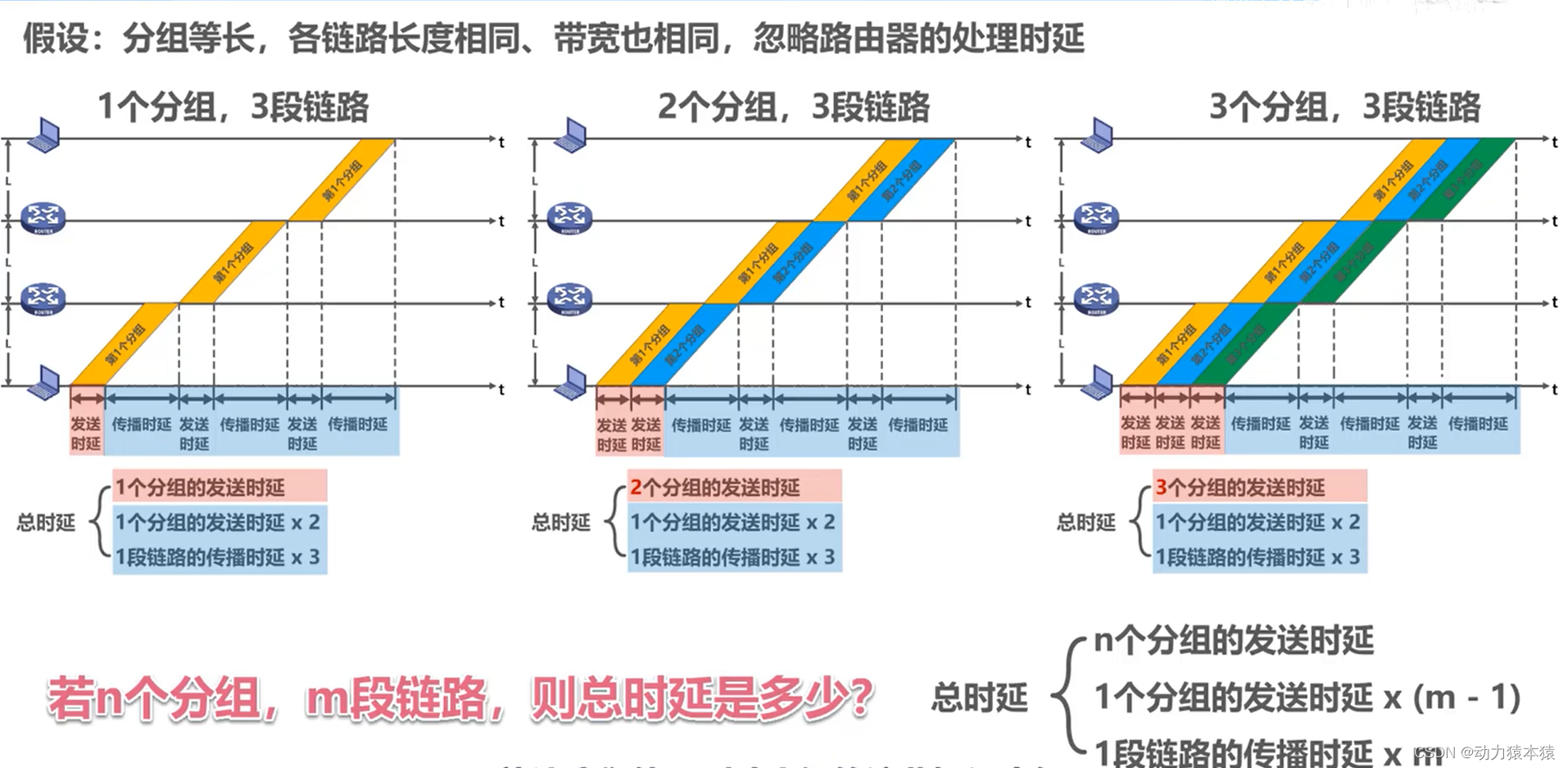
计算机网络概述习题拾遗
学习目标: 自下而上第一个提供端到端服务的层次 路由器、交换机、集线器实现的功能层 TCP/IP体系结构的网络接口层对应OSI体系结构的哪两个层次 分组数量对总时延的影响 如果这篇文章对您有帮助,麻烦点赞关注支持一下动力猿吧! 学习内容…...

你的电脑关机吗
目录 程序员为什么不喜欢关电脑? 电脑长时间不关机会怎样? 电脑卡顿 中度风险 硬件损耗 能源浪费 散热问题 软件问题 网络安全问题 程序员为什么不喜欢关电脑? 大部分人都会选择将电脑进行关机操作。其实这不难理解,毕竟人类都需要…...
flask+python儿童福利院管理系统pycharm毕业设计项目
本系统解决了儿童福利院管理事务中的主要问题,包括首页、个人中心、爱心人士管理、员工管理、后勤人员管理、儿童信息管理、院所风采管理、活动管理、食谱管理、领养流程管理、政策法规管理、楼栋管理、宿舍管理、领养申请管理、义工申请管理、捐赠信息管理、宿舍物…...

React:高阶组件|ref转发
高阶组件 参考文档:高阶组件 – React (reactjs.org) 高阶组件(Higher-Order Components,简称 HOC)是React中用于复用组件逻辑的一种高级技巧。具体而言:高阶组件是参数为组件,返回值为新组件的函数。 组件…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...
