数字的魅力之情有独钟的素数
情有独钟的素数
什么是素数
素数(Prime number)也称为质数,是指在非0自然数中,除了1与其本身之外不拥有其他因数的自然数。也就是说,素数需要满足两个条件:
- 大于1的整数;
- 只拥有1和其自身两个因数。
例子1
本文章的任务就是输出100以内的所有素数,如2、3、5、7、11、13…
先理清一下思路:
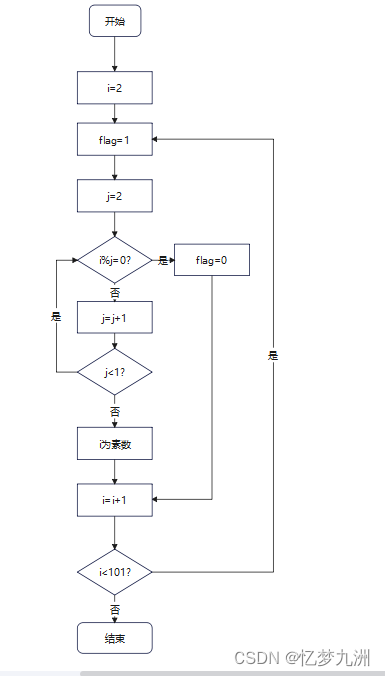
(1)需要有一个2~100的外循环,还要有一个小于当前数的因子内循环;
(2)需要有一个判断是否可整除的i语句(整除就是余数为0)。
求100以内的素数的思路如下图所示。
代码实现
实现代码如下:
Python
# 100以内的素数算法
prime = []
#从2开始遍厉到100
for i in range (2,101) :flag =1 #i是否力素数的标记# 因数应该是大于1小于自身的数for j in range (2, i):if i%j ==0: #一旦取模(余数)为0flag = 0 # 更改标记为0break # 直接跳出本循环if flag == 1: # 标记为 1,则为素数prime.append(i) # 添加到 prime 列表
print("100以内的素数:",prime)
Java
List<Integer> arr = new ArrayList<>();int flag ;for(int i=2;i<101;i++){flag =1;for (int j=2;j<i;j++){if(i%j==0){flag =0;break;}}if(flag==1){arr.add(i);}}System.out.println(arr);
输出结果如下:

例子2 “优化素数计算:从暴力求解到开方优化”
只要解决了问题就结束了吗?这可不是学习的态度。《诗经》有云:“如切如磋,如琢如磨。”其斯之谓与?我们可要精益求精啊。这段代码虽实现了我们的任务,但它的时间复杂度太大,100 以内的素数还可以,如果是1000或10000呢?
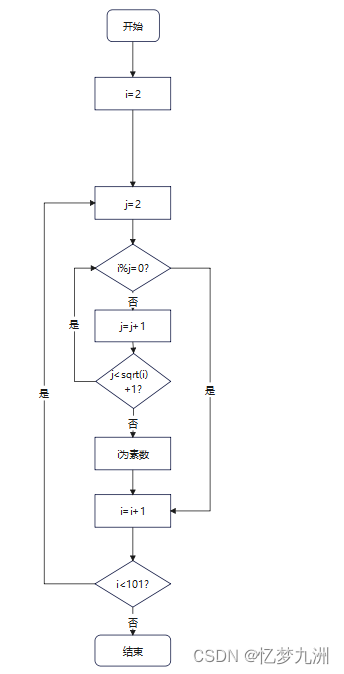
可是要怎样使时间复杂度变小呢?只有两个地方可以下手——要么是外循环,要么是内循环。我们知道:任意数若等于两个非0自然数的乘积,则这两个因子中至少有一个小于该数的二分之一。
当然,我们还可以再缩小一下范围,把“二分之一”缩减为“开方”,这样就大大缩减了内循环的运行时间。思路如下图所示。
代码实现
实现代码如下:
Python
# -*- coding: utf-8 -*-
import math#100以内的素数算法二
prime = []
#从2开始遍历到 100
for i in range (2,101) :#因数应该是大于1小于自身的开方+1for j in range(2,int(math.sqrt(i))+1):#一旦取模(余数)为0if i%j == 0:break #直接跳出本循环# 若余数均不0,则为素数else:prime.append(i) # 添加到 prime 列表中print("100以内的全部素数:",prime)
Java
List<Integer> arr = new ArrayList<>();int j;for(int i=2;i<101;i++){for (j=2;j<(int)Math.sqrt(i)+1;j++){if(i%j==0){break;}}if(j==(int)Math.sqrt(i)+1){arr.add(i);}}System.out.println(arr);
注意:例子二的内循环范围记得加1,否则输出结果错误
输出结果如下:

看,我们只改了一个值,便大大缩短了算法的运行时间,这就是思维逻辑的重要性。只要逻辑捋顺了,代码实现就很容易了。
例子3
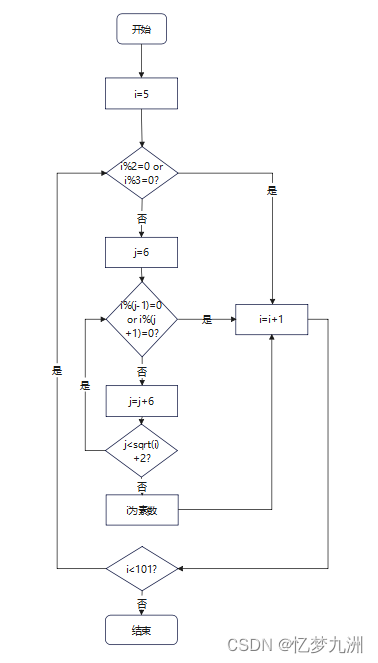
观察结果发现,5+1=6,7-1=6,11+1=12,13-1=12, 17+1=18,19-1=18,23+1=24…这些都是6的倍数,那我们当不是可以利用(6n-1)和(6n+1)两个公式便可以得到质数的排列了?那么下一个质数必该是6×4+1=35,再下个质数就是6×5-1=29,但是25并不是质数,因此排列的规律还需要我们一步步地分析。
我们先不看2和3,从5开始往后数,所有的素数都分布在6n(n≥1)左右两侧,即(6n-1)与(6n+1)。那以6为间距的其他数又是如何分布的呢?6n %6=0,(6n+2)%2=0,(6n+3)%3=0,(6n+4)%2=0,(6n+5)则又回到了(6n-1),一个循环结束了。
我们发现:除去2和3以外,所有的素数都是符合(6n-1)和(6n+1)规律的,但符合这两个公式的数字不一定就是素数,因此这是一个充分非必要条件,而不是充要条件。
据此,我们可以进一步缩小因子范围,思路如下图所示。
代码实现
实现代码如下:
Python
# -*- coding: utf-8 -*-
import math# 100 以内的素数算法三
prime = []
prime. extend([2, 3]) #已知2和3 是素数
# 从5开始遍历到 100
for i in range (5,101) :# 非素数时if i % 2 == 0 or i%3 ==0 :continue # 跳过后续操作,直接进入下一循环# 因数应该是大于1小于自身的开方+2,以6为单位for j in range(6, int(math.sqrt(i))+2,6):# 当可以整除6 的倍数时两侧的数字也为非素数if i%(j-1) == 0 or i%(j+1) ==0:break # 直接跳出本循环# 若余数均不为O,则为素数else:prime.append(i)
# 添加到 prime 列表中
print("100以内的全部素数:",prime)
Java
List<Integer> arr = new ArrayList<>();arr.add(2);arr.add(3);int j;for(int i=5;i<101;i++){if (i%2==0 || i%3==0)continue;for (j=6;j<(int)Math.sqrt(i)+2;j+=6){if(i%(j-1)==0 || i%(j+1)==0){break;}}if(j>=(int)Math.sqrt(i)+2){arr.add(i);}}System.out.println(arr);
注意:continue 和 break 非常好用,不熟悉它们的用法的读者请务必掌握。
输出结果如下:

“素数的广泛应用与未解决的数学难题”
这么一看果然“顺眼”多了,虽然思路让人不好理解,但多看几遍还是能理解的。一般来说,实现相同功能的不同代码,越简洁的就越晦涩,运行时间越少的也越难懂。当然,素数的检测算法远不止于此,还有费马素性测试(Fermat primality test)、米勒-拉宾素性测试 (Miller-Rabin primality test)、Solovay-Strassen 测试、卢卡斯-菜默素性测试 (Lucas-Lehmer primality test)和埃拉托斯特尼筛法等。素数在自然数中的分布极其复架,其被广泛应用到密码学中,即在公钥中插入素数并进行编码,以此达到提高破译难度的目的。
同时,素数领域还存在许多数学家们一直无法解决的难题,最著名的莫过于“哥德巴赫猜想”和“黎曼猜想”。哥德巴赫和黎曼在数学界都是举足轻重的人物。哥德巴赫猜想是:“是否每个大于2的偶数都可写成两个素数之和?”娶曼猜想是:“素数出现的频率与黎曼 ζ \zeta ζ函数紧密相关。”这两个猜想虽然未能被完全验证,但已经被广泛应用,黎曼猜想甚至已经成为当今数学文献中一千多条数学命题的前提。
相关文章:

数字的魅力之情有独钟的素数
情有独钟的素数 什么是素数 素数(Prime number)也称为质数,是指在非0自然数中,除了1与其本身之外不拥有其他因数的自然数。也就是说,素数需要满足两个条件: 大于1的整数;只拥有1和其自身两个…...

Vue2源码梳理:render函数的实现
render 在 $mount 时,会调用 render 方法在写 template 时,最终也会转换成 render 方法Vue 的 _render 方法是实例的一个私有方法,它用来把实例渲染成一个虚拟 Node它的定义在 src/core/instance/render.js 文件中,它返回的是一个…...
flask+python企业产品订单管理系统938re
在设计中采用“自下而上”的思想,在创新型产品提前购模块实现了个人中心、个体管理、发布企业管理、投资企业管理、项目分类管理、产品项目管理、个体投资管理、企业投资管理、个体订单管理、企业订单管理、系统管理等的功能性进行操作。最终,对基本系统…...

Vue2源码梳理:关于数据驱动,与new Vue时的初始化操作
数据驱动 1 )概述 vue的一个核心思想,就是数据驱动 所谓数据驱动,就是指视图是由数据驱动生成的 对视图的修改并不会直接操作dom,而是通过修改数据 它相比我们传统的前端开发,如使用 jQuery 的前端库直接去修改 dom…...
【C++航海王:追寻罗杰的编程之路】关于模板,你知道哪些?
目录 1 -> 泛型编程 2 -> 函数模板 2.1 -> 函数模板概念 2.2 -> 函数模板格式 2.3 -> 函数模板的原理 2.4 -> 函数模板的实例化 2.5 -> 函数参数的匹配原则 3 -> 类模板 3.1 -> 类模板的定义格式 3.2 -> 类模板的实例化 1 -> 泛型编…...
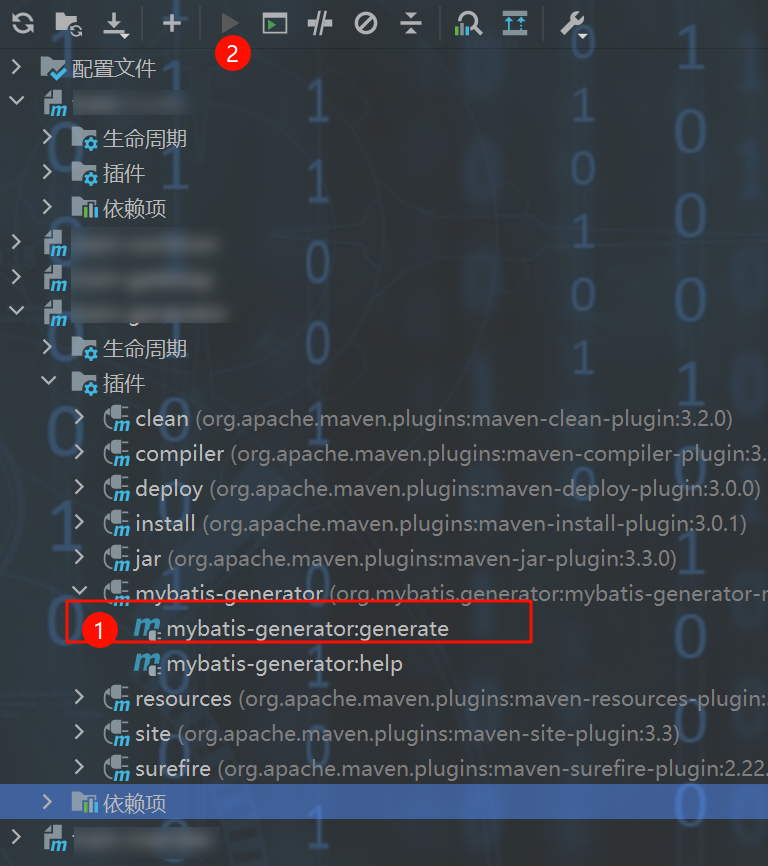
分布式springboot 3项目集成mybatis官方生成器开发记录
文章目录 说明实现思路实现步骤第一步:创建generator子模块第二步:引入相关maven插件和依赖第三步:编写生成器配置文件第四步:运行查看结果 说明 该文章为作者开发学习记录,方便以后复习和交流主要内容为:…...

算法学习——LeetCode力扣回溯篇4
算法学习——LeetCode力扣回溯篇4 332. 重新安排行程 332. 重新安排行程 - 力扣(LeetCode) 描述 给你一份航线列表 tickets ,其中 tickets[i] [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。 所有这些机票…...
multimap)
c++ STL系列——(六)multimap
C标准模板库(STL)是C编程中不可或缺的一部分,它提供了一系列的容器、算法和函数模板,以简化常见的数据结构和算法的实现。在STL中,multimap是一个非常有用的容器,它提供了一种键值对的存储方式,…...

Json-序列化字符串时间格式问题
序列化字符串时间格式问题 一、项目场景二、问题描述三、解决方案 一、项目场景 最近C#中需要将实体进行json序列化,使用了Newtonsoft.Json public static void TestJson(){DataTable dt new DataTable();dt.Columns.Add("Age", Type.GetType("Sys…...
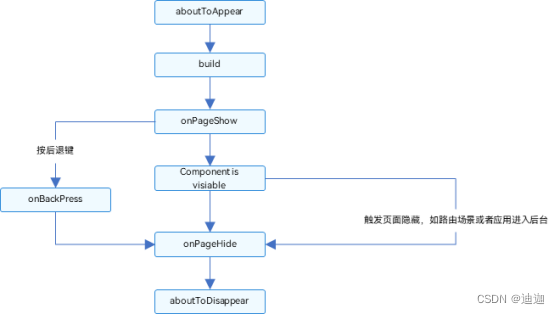
HarmonyOS鸿蒙学习基础篇 - 自定义组件(一)
前言 在ArkUI中,UI显示的内容均为组件,由框架直接提供的称为系统组件,由开发者定义的称为自定义组件。在进行 UI 界面开发时,通常不是简单的将系统组件进行组合使用,而是需要考虑代码可复用性、业务逻辑与UI分离&#…...
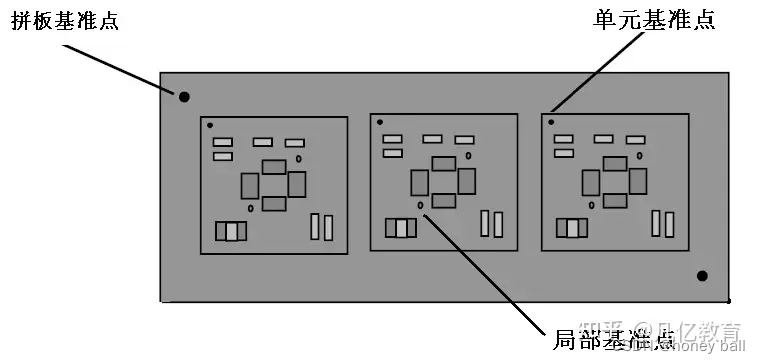
开窗,挖槽,放电齿,拼版
我们在阻焊层画线,就相当于去掉绿油阻焊,开窗一般是用在大电流走线的时候。先画要走的导线,之后切换到TopSolder或者Bottom Solder层,然后Place->line 画一条和原来先粗细一样的线即可!但走电流的仍然是导线&#x…...

[Vue的组件通讯.sync修饰]Vue中.sync的使用方法和实现的方式 代码注释
目录 .sync的使用方法1. 在父组件中,将需要传递给子组件的数据使用v-bind绑定到子组件的props中,并在属性名后加上.sync修饰符,如下所示:2. 在子组件中,将需要传递给父组件的数据使用$emit方法触发一个名为update:valu…...
Java 基于springboot+vue在线外卖点餐系统,附源码
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝12w、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇…...
Decian 12.x基于LNMP安装phpIPAM(IP管理系统)
phpipam是一个开源Web IP地址管理应用程序(IPAM)。其目标是提供轻便,且有用的IP地址管理系统。它是基于PHP的应用程序,具有MySQL数据库后端,使用jQuery库,ajax和HTML5 / CSS3功能。 在Debian 12中&…...

【多模态MLLMs+图像编辑】MGIE:苹果开源基于指令和大语言模型的图片编辑神器(24.02.03开源)
项目主页:https://mllm-ie.github.io/ 论文 :基于指令和多模态大语言模型图片编辑 2309.Guiding Instruction-based Image Editing via Multimodal Large Language Models (加州大学圣巴拉分校苹果) 代码:https://github.com/appl…...

hpp文件:C++开发中的利器
1 什么是hpp文件? hpp文件是C程序中一种特殊头文件,它可以包含类的声明和实现。与传统的h文件相比,hpp文件具有以下特点: 将类的声明和实现放在同一个文件里,减少了代码量,提高了代码的可读性。无需再将c…...

如何查看电脑连接的wifi的密码
问题 很多时候我们电脑连上wifi之后就把密码忘记了,这个时候如果同事问自己密码是多少,如果作为程序员说不知道是不是感觉有点不好意思,哈哈…… 解决 我使用的是windows电脑,就以windows为例说明下自己是如何查看的。 打开wi…...
QTabWidget和QTabBar控件样式设置(qss)
QTabWidget和QTabBar控件样式设置 1、QTabWidget样式可自定义的有哪些示例:效果图 2、QTabBar样式可自定义的有哪些示例效果图 1、QTabWidget样式可自定义的有哪些 QTabWidget::pane{} 定义tabWidgetFrameQTabWidget::tab-bar{} 定义TabBar的位置QTabWidget::tab{}定…...
【智能家居入门3】(MQTT服务器、MQTT协议、微信小程序、STM32)
前面已经写了三篇博客关于智能家居的,服务器全都是使用ONENET中国移动,他最大的优点就是作为数据收发的中转站是免费的。本篇使用专门适配MQTT协议的MQTT服务器,有公用的,也可以自己搭建(应该要钱)…...

C语言第二十四弹---指针(八)
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】 指针 1、数组和指针笔试题解析 1.1、字符数组 1.1.1、代码1: 1.1.2、代码2: 1.1.3、代码3: 1.1.4、代码4: 1…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...
