学习总结16
# 【模板】最小生成树
## 题目描述
如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出 `orz`。
## 输入格式
第一行包含两个整数 N,M,表示该图共有 N 个结点和 M 条无向边。
接下来 M 行每行包含三个整数 Xi,Yi,Zi,表示有一条长度为 Zi 的无向边连接结点 Xi,Yi。
## 输出格式
如果该图连通,则输出一个整数表示最小生成树的各边的长度之和。如果该图不连通则输出 `orz`。
## 样例 #1
### 样例输入 #1
```
4 5
1 2 2
1 3 2
1 4 3
2 3 4
3 4 3
```
### 样例输出 #1
```
7
```
## 提示
数据规模:
对于 20% 的数据,N<= 5,M<= 20。
对于 40% 的数据,N<= 50,M<= 2500。
对于 70% 的数据,N<= 500,M<= 10^4。
对于 100% 的数据:1<= N<= 5000,1<= M<= 2* 10^5,1<= Zi <= 10^4。
解题思路
利用prim算法来生成树,但是需要一点优化,如果使用朴素prim有几个数据点会超时,在优化代码中我们只需要用一个数组来保存集合到与集合相邻的点的距离。
朴素代码
#include <bits/stdc++.h>
using namespace std;
int g[6010][6010];
int j[5010];
int g1[5010];
int main()
{int x,y,n,m;int a,b,c,sum,t,min1,z;scanf("%d%d",&n,&m);for(x=1;x<=n;x++){for(y=1;y<=n;y++)g[x][y]=999999;}for(x=0;x<m;x++){scanf("%d%d%d",&a,&b,&c);if(c<g[a][b])g[a][b]=c;if(c<g[b][a])g[b][a]=c;}t=1;sum=0;g1[1]=1;j[1]=1;while(t<n){min1=99999;for(x=1;x<=t;x++){y=g1[x];for(z=1;z<=n;z++){if(min1>g[y][z]&&j[z]!=1){min1=g[y][z];a=y;b=z;}}}if(min1==99999){printf("orz");return 0;}t++;g1[t]=b;sum+=g[a][b];j[b]=1;}printf("%d",sum);return 0;
}优化代码
#include <bits/stdc++.h>
using namespace std;
int g[5010][5010];
int j[5010];
int g1[5010];
int ju[5010];
int main()
{int x,y,n,m;int a,b,c,sum,t,min1,z;scanf("%d%d",&n,&m);for(x=1;x<=n;x++){for(y=1;y<=n;y++)g[x][y]=999999;}for(x=0;x<m;x++){scanf("%d%d%d",&a,&b,&c);if(c<g[a][b])g[a][b]=c;if(c<g[b][a])g[b][a]=c;}t=1;sum=0;g1[1]=1;j[1]=1;for(x=1;x<=n;x++){if(x!=1)ju[x]=g[x][1];}while(t<n){min1=99999;for(x=1;x<=n;x++){if(ju[x]<min1&&j[x]!=1){min1=ju[x];b=x;}}if(min1==99999){printf("orz");return 0;}t++;g1[t]=b;sum+=min1;j[b]=1;for(x=1;x<=n;x++){if(g[b][x]<ju[x]&&ju[x]!=99999)ju[x]=g[b][x];}}printf("%d",sum);return 0;
}# 拆地毯
## 题目背景
还记得 NOIP 2011 提高组 Day1 中的铺地毯吗?时光飞逝,光阴荏苒,三年过去了。组织者精心准备的颁奖典礼早已结束,留下的则是被人们踩过的地毯。请你来解决类似于铺地毯的另一个问题。
## 题目描述
会场上有 n 个关键区域,不同的关键区域由 m 条无向地毯彼此连接。每条地毯可由三个整数 u、v、w 表示,其中 u 和 v 为地毯连接的两个关键区域编号,w 为这条地毯的美丽度。
由于颁奖典礼已经结束,铺过的地毯不得不拆除。为了贯彻勤俭节约的原则,组织者被要求只能保留至多 K 条地毯,且保留的地毯构成的图中,任意可互相到达的两点间只能有一种方式互相到达。换言之,组织者要求新图中不能有环。现在组织者求助你,想请你帮忙算出这至多 K 条地毯的美丽度之和最大为多少。
## 输入格式
第一行包含三个正整数 n、m、K。
接下来 m 行中每行包含三个正整数 u、v、w。
## 输出格式
只包含一个正整数,表示这 K 条地毯的美丽度之和的最大值。
## 样例 #1
### 样例输入 #1
```
5 4 3
1 2 10
1 3 9
2 3 7
4 5 3
```
### 样例输出 #1
```
22
```
## 提示
选择第 1、2、4 条地毯,美丽度之和为 10 + 9 + 3 = 22。
若选择第 1、2、3 条地毯,虽然美丽度之和可以达到 10 + 9 + 7 = 26,但这将导致关键区域 1、2、3 构成一个环,这是题目中不允许的。
1<=n,m,k<=100000
解题思路
只要把所有地毯按照美丽度排序,然后从大到小进行生成树就行了。
代码
#include <bits/stdc++.h>
using namespace std;
int g[100010];
struct ss
{int u;int v;int w;
}j[100010];
int n,m,k;
int u,v,w;
int cmp(ss x,ss y)
{return x.w>y.w;
}
int find1(int x)
{if(g[x]!=x)g[x]=find1(g[x]);return g[x];
}
int main()
{int x,y,q,e,sum=0;scanf("%d%d%d",&n,&m,&k);for(x=1;x<=n;x++){g[x]=x;}for(x=1;x<=m;x++){scanf("%d%d%d",&j[x].u,&j[x].v,&j[x].w);}sort(j+1,j+m+1,cmp);for(x=1,y=0;x<=m&&y<k;x++){q=find1(j[x].u);e=find1(j[x].v);if(q!=e){g[q]=e;sum+=j[x].w;y++;}}printf("%d",sum);return 0;
}相关文章:

学习总结16
# 【模板】最小生成树 ## 题目描述 如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出 orz。 ## 输入格式 第一行包含两个整数 N,M,表示该图共有 N 个结点和 M 条无向边。 接下来 M 行每行包含三个整数 …...
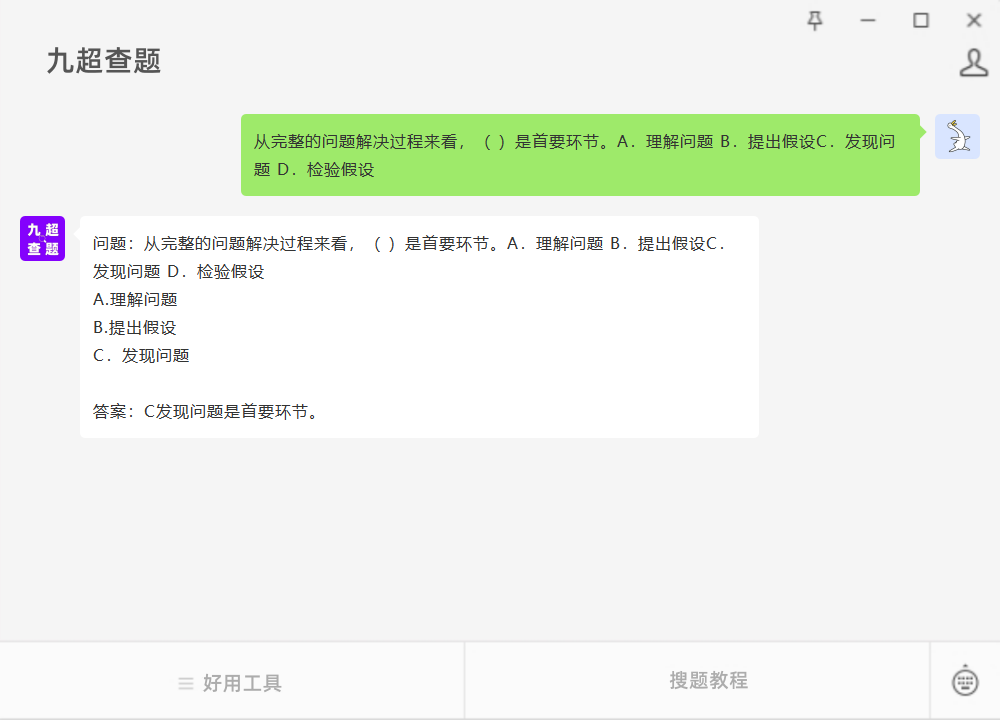
问题:从完整的问题解决过程来看,( )是首要环节。A.理解问题 B.提出假设C.发现问题 D.检验假设 #学习方法#学习方法
问题:从完整的问题解决过程来看,( )是首要环节。A.理解问题 B.提出假设C.发现问题 D.检验假设 A.理解问题 B.提出假设 C.发现问题 参考答案如图所示...

服务器感染了.mallox勒索病毒,如何确保数据文件完整恢复?
导言: 在当今数字化的世界中,恶意软件已成为企业和个人数据安全的一大威胁,其中.mallox勒索病毒是最为恶劣的之一。本文91数据恢复将介绍.mallox勒索病毒的特点,以及如何恢复被其加密的数据文件以及预防措施。 如果您正在经历勒索…...

Android java基础_多态性
一.Android Java基础_多态性 向上转换:只能定义被子类覆写的方法,不能调用在子类中定义的方法。 class Father {private int money; public int getMoney() {return money; }public void setMoney(int money) {this.money money; }public void printInfo() {Syst…...

面试前的准备
目录: 面试前的准备Java程序员校招与社招的区别校招与社招的区别:Java程序员投递简的正确方式投递简历时的误区简历投递时间Java程序员如何应对面试邀约Java程序员如何对公司做背调面试前的技术准备 面试前的准备 Java程序员校招与社招的区别 校招和社招…...

前端架构: 本地调试脚手架的2种方式
一、 调试简单的脚手架方式 假定脚手架名称是 xxx 1 )方式1 在xxx脚手架项目目录的上一级,执行 npm i -g xxx这时候,就可以本地调试脚手架,在前文中已经说明软链的作用参考:https://blog.csdn.net/Tyro_java/article…...

现阶段适用于 单一架构 还是 分布式架构 ?
单体架构: 优势:简单直接,易于理解和开发,适用于小型应用或刚刚开始的项目。劣势:扩展性受限,只能通过增加服务器的数量来提高处理能力;所有模块都部署在一个单独的服务器或容器中,…...

掌握Go并发:Go语言并发编程深度解析
🏷️个人主页:鼠鼠我捏,要死了捏的主页 🏷️系列专栏:Golang全栈-专栏 🏷️个人学习笔记,若有缺误,欢迎评论区指正 前些天发现了一个巨牛的人工智能学习网站,通俗易懂&…...

创建一个多进程服务器和多线程服务器
多进程服务器 #include<myhead.h> #define PORT 8888 //端口号 #define IP "192.168.10.10" //IP地址//定义信号处理函数,用于回收僵尸进程 void handler(int signo) {if(signo SIGCHLD){while(waitpid(-1, NULL, WNOHAN…...
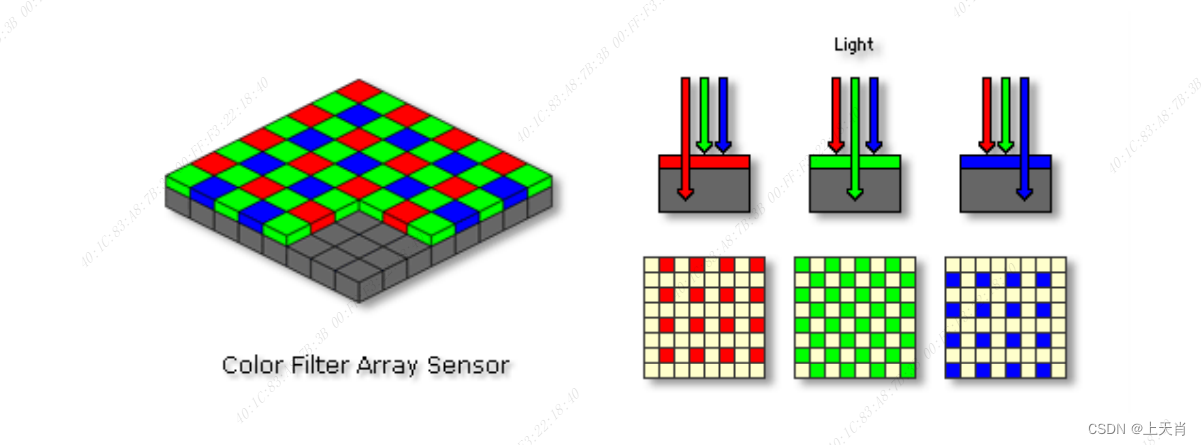
相机图像质量研究(18)常见问题总结:CMOS期间对成像的影响--CFA
系列文章目录 相机图像质量研究(1)Camera成像流程介绍 相机图像质量研究(2)ISP专用平台调优介绍 相机图像质量研究(3)图像质量测试介绍 相机图像质量研究(4)常见问题总结:光学结构对成像的影响--焦距 相机图像质量研究(5)常见问题总结:光学结构对成…...

18.谈谈你对JSON的理解
JSON 是一种基于文本的轻量级的数据交换格式。它可以被任何的编程语言读取和作为数据格式来传递。 在项目开发中,使用 JSON 作为前后端数据交换的方式。在前端通过将一个符合 JSON 格式的数据结构序列化为 JSON 字符串,然后将它传递到后端,后…...

绝地求生:“觉醒之旅”通行证曝光,西游主题通行证及成长型武器即将上线
随着27赛季即将结束,有关28.1版本的皮肤及通行证内容也被爆料出来,本次通行证为工坊通行证,和去年四圣兽通行证为同一类型,将于2月7日更新至正式服 除了通行证获取工坊币还是可以开箱获取并兑换一些奖励 先看通行证 四个套装应该分…...

JS如何判断普通函数与异步(async)函数
这里可以先打印一下普通函数和异步(async)函数的结构,如下图 可以看出两者原型链,普通函数的原型链指向的是一个函数,异步(async)函数原型链指向的是一个AsyncFunction,这时就会想到…...

ndk-r20b 编译 boost 1.74。
ndk-r20b 编译 boost 1.74,这是 ndk-r20b 支持得最大 boost 版本,再大就没法编译支持了,本文介绍方法是完整编译,不需要完整编译请转移到github,boost for android 得开源项目。 1.74 boost ,安卓上面得版本…...

尚硅谷最新Node.js 学习笔记(四)
目录 八、express框架 8.1、express介绍 8.2、express使用 express下载 express初体验 8.3、express路由 什么是路由? 路由的使用 获取请求参数 获取路由参数 8.4、express响应设置 8.5、express中间件 什么是中间件? 中间件的作用 中间件…...

掌握XGBoost:GPU 加速与性能优化
导言 XGBoost是一种强大的机器学习算法,但在处理大规模数据时,传统的CPU计算可能会变得缓慢。为了提高性能,XGBoost可以利用GPU进行加速。本教程将介绍如何在Python中使用XGBoost进行GPU加速以及性能优化的方法,并提供相应的代码…...
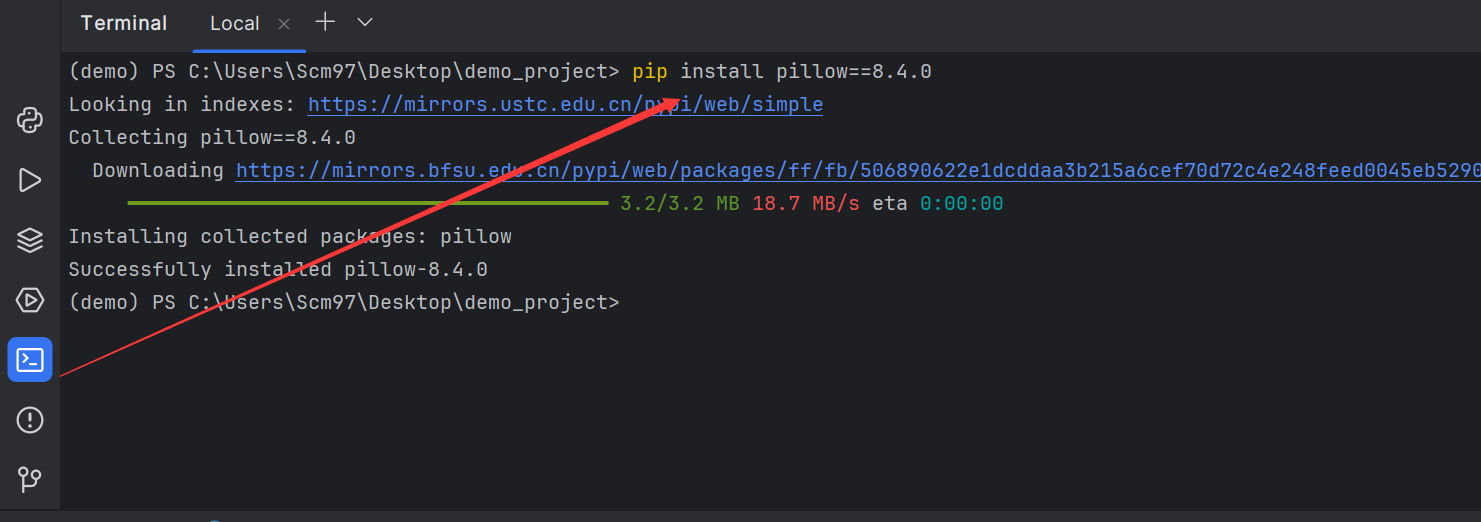
【2024年毕设系列】如何使用Anaconda和Pycharm
【2024年毕设系列】如何使用Anaconda和Pycharm 视频教程地址:【2024毕设系列】Anaconda和Pycharm如何使用_哔哩哔哩 Hi,各位好久不见,这里是肆十二,首先在这里给大伙拜年了。 诸位过完年之后估计又要开始为了大作业和毕业设计头疼…...
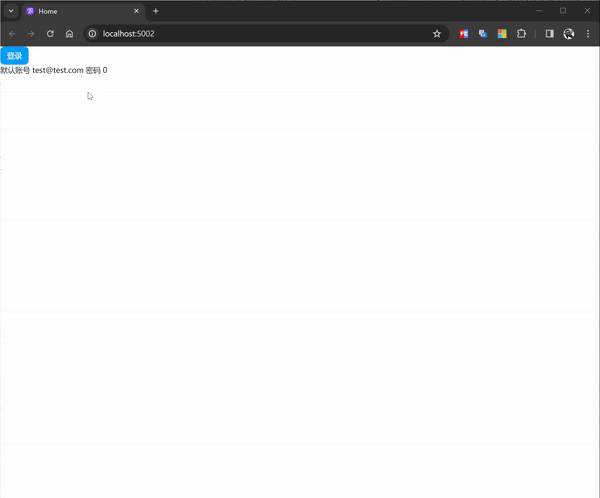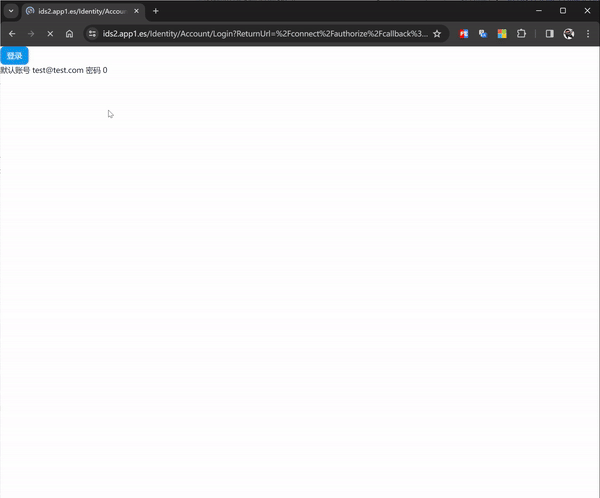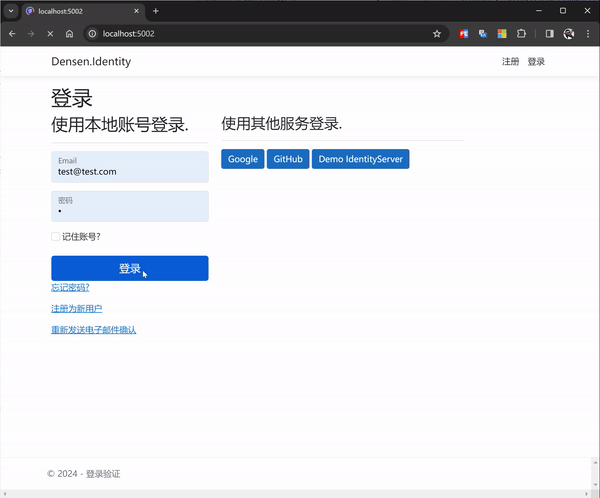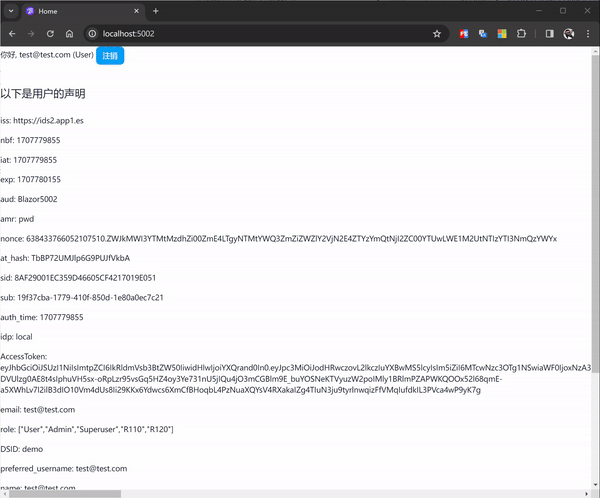
Blazor OIDC 单点登录授权实例5 - 独立SSR App (net8 webapp ) 端授权
目录: OpenID 与 OAuth2 基础知识Blazor wasm Google 登录Blazor wasm Gitee 码云登录Blazor OIDC 单点登录授权实例1-建立和配置IDS身份验证服务Blazor OIDC 单点登录授权实例2-登录信息组件wasmBlazor OIDC 单点登录授权实例3-服务端管理组件Blazor OIDC 单点登录授权实例4 …...
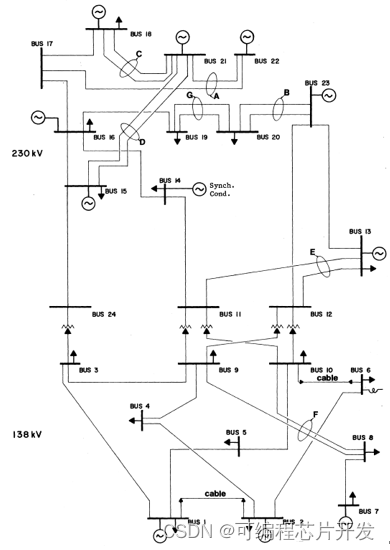
基于蒙特卡洛的电力系统可靠性分析matlab仿真,对比EDNS和LOLP
目录 1.课题概述 2.系统仿真结果 3.核心程序与模型 4.系统原理简介 1.课题概述 电力系统可靠性是指电力系统按可接受的质量标准和所需数量不间断地向电力用户供应电力和电能量的能力的量度,包括充裕度和安全性两个方面。发电系统可靠性是指统一并网的全部发电机…...

Spring boot整合redisson报错
Spring boot整合redisson报错 org.redisson.client.RedisConnectionException: Unable to connect to Redis server: localhost/127.0.0.1:6379 原因 原因是计算机连接不上redis导致的 解决方案 重启redis 在redis文件目录下打开cmd 1.检查redis是否在运行 redis-cli p…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
