基于蒙特卡洛的电力系统可靠性分析matlab仿真,对比EDNS和LOLP
目录
1.课题概述
2.系统仿真结果
3.核心程序与模型
4.系统原理简介
1.课题概述
电力系统可靠性是指电力系统按可接受的质量标准和所需数量不间断地向电力用户供应电力和电能量的能力的量度,包括充裕度和安全性两个方面。发电系统可靠性是指统一并网的全部发电机组按可接受标准及期望数量满足电力系统的电力和电能量需求的能力的量度。发电系统可靠性指标可以分为确定性和概率性两类。过去曾广泛应用确定性可靠性指标来指导电力系统规划和运行,如百分数备用法和偶然故障备用法。目前已逐渐被概率性可靠性指标所代替。
概率法常用的可靠性指标有:电力不足概率(Loss of Load Probability, LOLP)和期望缺供电量(Expected Demand Not Served, EDNS)是评估电力系统可靠性的两个重要指标。通过随机法和蒙特卡洛法分别对这两个指标进行仿真分析。
2.系统仿真结果


从仿真可以看到,对于电力不足概率指标LOLP,LOLP值的可能性随着LOLP值得变大而下降,这是因为在模拟元件失效过程中,由于元件失效而导致的电力不足的可能性会出现,但是其大概率的电力不足出现概率较低,而小概率的电力不足情况出现概率较大。
对于停电功率期望值指标EDNS,EDNS值发生可能性的随着EDNS值得变大而下降,即在实际过程中,随着元件失效而发生停电的期望值,其大概率的停电功率出现概率较低,而小概率的停电功率情况出现概率较大。
3.核心程序与模型
版本:MATLAB2022a
.....................................................................while (Flag == 1)TTT = TTT + 1;%断开选定的线路if TTT == 1BRANCHo(Cut_info,3:end) = 0;All_Del_Point= [All_Del_Point;Cut_info'];else%断开相邻的线路Inders1 = find(BRANCHo(:,1) == Cut_info(1));Inders2 = find(BRANCHo(:,1) == Cut_info(2));Inders3 = find(BRANCHo(:,2) == Cut_info(1));Inders4 = find(BRANCHo(:,2) == Cut_info(2)); Inders = unique([Inders1;Inders2;Inders3;Inders4]);%随机选择tmpsss = randperm(length(Inders));Inders_sel = Inders(tmpsss(1));BRANCHo(Inders_sel,3:end) = 0;All_Del_Point= [All_Del_Point;Inders_sel];end%根据信息节点的Pdi和Pmi进行失去控制for i1 = 1:N-1P1 = rand(1);P2 = rand(1);if P1 <= Pdi(i1) | (P1 > Pdi(i1) & P2 <= Pmi) %调度中心认为线路处理初始状态BRANCHo(i1,3:end) = 0;All_Del_Point= [All_Del_Point;i1];end end%对此时的电器网络进行计算潮流Ak = func_Admittance_matrix(BUSo,BRANCHo);F = Ak * Pp;%判断是否越限for jjj = 1:length(F)if (abs(F(jjj))) <= (abs(Fmax(jjj)))%没有越限,则进行步骤5P = rand();if P <= PHFlag = 1;%被选中,则继续步骤2,即重新循环elseFlag = 0;%未被选中,则继续步骤6,跳出循环endelse%有越限,则进行步骤3 %先进行LP优化,这里使用PSO进行优化 [V_score2,PP] = func_pso_calculate_min(Bus_Num,15,Pp);%再计算潮流Ak = func_Admittance_matrix(BUSo,BRANCHo);F = Ak*(1+g)*PP;if sum(abs(F)) > sum(abs(Fmax))Flag = 1;else%没有越限,则进行步骤5P = rand();if P <= PHFlag = 1;%被选中,则继续步骤2,即重新循环elseFlag = 0;%未被选中,则继续步骤6,跳出循环endendendendendAll_Del_Point = unique(All_Del_Point);LL = length(Fo);Fedns = zeros(LL,1);%对于断掉的点取1,其余取0.Fedns(All_Del_Point) = 1;deltaP = abs(Fo-F);E1(m) = sum(Fedns.*deltaP)/LL;NUMSS(:,m) = NUMS;[cdf,PAPR] = ecdf(E1);
EDNS = E1;%%
figure;
semilogy(100*PAPR(1:end-5),1-cdf(1:end-5),'b-o','LineWidth',1);
xlabel('edns');
ylabel('The cumulative probability of failure probability');if NUM_Delete == 1save attack41.mat PAPR cdf EDNS NUMSS
end
if NUM_Delete == 2save attack42.mat PAPR cdf EDNS NUMSS
end
02_027m4.系统原理简介
基于蒙特卡洛的仿真思想,并根据每次产生的随机数种子,进行随机的失效模拟,元件失效过程使用马尔科夫过程建模产生。首先随机模拟一个元件失效的情况,对一个元件失效以及对应的连锁故障情况进行仿真分析。然后随机模拟二个元件失效的情况,对二个元件失效以及对应的连锁故障情况进行仿真分析。而对于三个甚至更多元件失效的情况,本文不做考虑,这是因为当出现三个或者更多的元件失效的情况,整个电力系统网络基本会发生大规模崩溃的情况,在这种情况下做可靠性评估没有实际的价值,故不做这方面的研究。
在本课题中,使用IEEE24-RTS电力网络系统作为案例进行分析
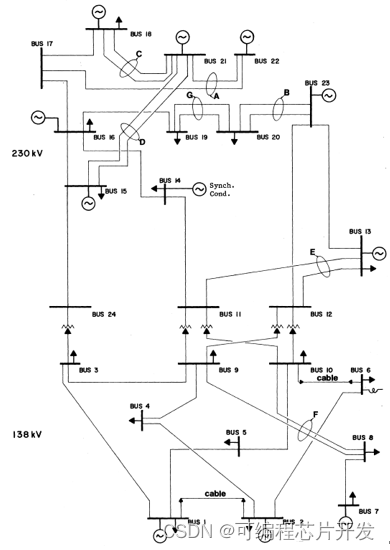
这里采用的仿真步骤如下:
由于我们需要考虑随机断开一条线路或者两条线路的系统的稳定性分析,因此,我们主要通过随机循环的思想,每次循环随机的断开线路,然后分析断开这条线路对系统造成的影响进行仿真分析。
一般情况下,对系统稳定性评估的分析方法主要是分析断开后故障网络的是否正常工作(即分析其是否崩溃)
通常,当断开一条线路的时候,往往会由于该线路的断开而导致其他的线路的连锁故障,从而导致整个系统的影响,但是这种连锁的情况在概率统计中,并不是必然事件,而是随机事件,因此,这里我们设计如下的故障及稳定性分析方法:
第一:首先随机的移除信息网络的信息节点,并计算对应的信息节点的传输信息时的延迟概率P。
第二:随机的选择故障线路,并断开该线路,并更新响应的网络参数;
第三:根据网络参数,通过直流法进行最优潮流的计算(DC OPF),并判断潮流是否存在越限,如果存在越限,则通过LP优化算法进行第四步操作,如果没有越限,则进行第五步操作。
第四:当存在越限的时候,那么基于随机的概率,并采用轮盘赌算法选择随机跳开的线路,并进行再次转入步骤二的操作。
第五:当不存在越限的时候,那么通过一个随机的小概率Ph选择需要跳开的线路,如果存在线路被选择,那么进入步骤二开始操作,否则进入步骤六。
第六:本次蒙特卡洛循环结束,进入下一次循环。
5.完整工程文件
v
相关文章:

基于蒙特卡洛的电力系统可靠性分析matlab仿真,对比EDNS和LOLP
目录 1.课题概述 2.系统仿真结果 3.核心程序与模型 4.系统原理简介 1.课题概述 电力系统可靠性是指电力系统按可接受的质量标准和所需数量不间断地向电力用户供应电力和电能量的能力的量度,包括充裕度和安全性两个方面。发电系统可靠性是指统一并网的全部发电机…...

Spring boot整合redisson报错
Spring boot整合redisson报错 org.redisson.client.RedisConnectionException: Unable to connect to Redis server: localhost/127.0.0.1:6379 原因 原因是计算机连接不上redis导致的 解决方案 重启redis 在redis文件目录下打开cmd 1.检查redis是否在运行 redis-cli p…...

【AIGC】Stable Diffusion的ControlNet插件
ControlNet 介绍 ControlNet 插件是 Stable Diffusion 中的一个重要组件,用于提供对模型的控制和调整。以下是 ControlNet 插件的主要特点和功能: 模型控制: ControlNet 允许用户对 Stable Diffusion 中的模型进行精细的控制和调整。用户可以…...
【蓝桥杯单片机入门记录】认识单片机
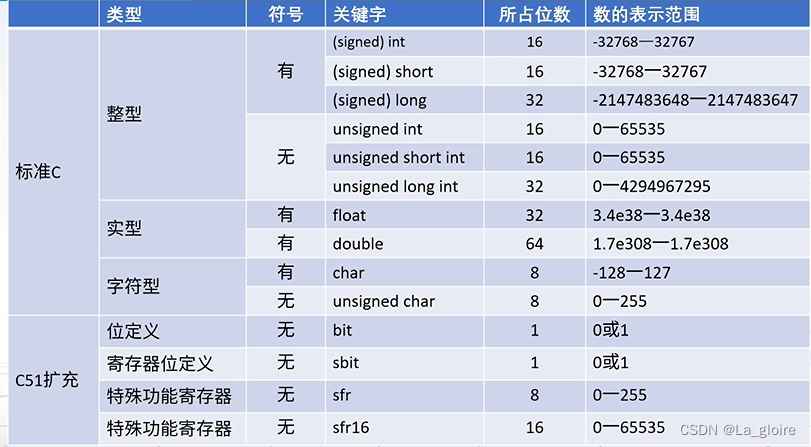
目录 单片机硬件平台 单片机的发展过程 单片机开发板 单片机基础知识 电平 数字电路中只有两种电平:高和低 二进制(8421码) 十六进制 二进制数的逻辑运算 “与” “或” “异或” 标准C与C51 如何学好单片机 端正学习的态度、培…...

Rust 数据结构与算法:3栈:用栈实现符号匹配
1、符号匹配 如: (56)(78)/(43)、{ { ( [ ] [ ])}}、(ab)(c*d)func() 等各类语句的符号匹配。 这里我们关注的不是数字而是括号,因为括号更改了操作优先级,限定了语言的语义,这是非常重要的。如果括号不完整,那么整个…...

用ESP8266快速实现WIFI红外遥控器(SoC模式)
1,硬件结构图 主要使用了esp8266 wifi模块和红外串口通讯模块。有了红外串口通讯模块,省去了单片机的串口通讯和红外编码程序,大大缩短开发时间。因为红外通讯模块不支持3.3VTTL电平,所以两个模块之间加了一个2路电平转换模块&…...

微服务OAuth 2.1认证授权可行性方案(Spring Security 6)
文章目录 一、背景二、微服务架构介绍三、认证服务器1. 数据库创建2. 新建模块3. 导入依赖和配置4. 安全认证配置类 四、认证服务器测试1. AUTHORIZATION_CODE(授权码模式)1. 获取授权码2. 获取JWT 2. CLIENT_CREDENTIALS(客户端凭证模式) 五、Gateway1.…...
Maui blazor ios 按设备类型设置是否启用safeArea
需求,新做了个app, 使用的是maui blazor技术,里面用了渐变背景,在默认启用SafeArea情况下,底部背景很突兀 由于现版本maui在SafeArea有点bug,官方教程的<ContentPage SafeAreafalse不生效,于…...
C#系列-使用 Minio 做图片服务器实现图片上传 和下载(13)
1、Minio 服务器下载和安装 要在本地安装和运行 MinIO 服务器,你可以按照以下 步骤进行操作: 1. 访问 MinIO 的官方网站:https://min.io/,然后 点击页面上的”Download”按钮。 2. 在下载页面上,选择适合你操作系统的 …...

生活篇——华为手机去除负一屏
华为手机去除如下图的恶心负一屏 打开华为的应用市场app 进入:我的-设置-国家/地区(改为俄罗斯)-进入智慧助手检查更新并更新智慧助手。 然后重复开始的操作,将地区改回中国,这样就没有负一屏了。...
2024牛客寒假算法基础集训营2-c Tokitsukaze and Min-Max XOR
来源 题目 Tokitsukaze 有一个长度为 n 的序列 a1,a2,…,an和一个整数 k。 她想知道有多少种序列 b1,b2,…,bm满足: 其中 ⊕\oplus⊕ 为按位异或,具体参见 百度百科:异或 答案可能很大,请输出 mod1e97 后的结果。 输入描述…...

C语言:指针的基础详解
目录 1. 内存 2. 取地址& 3. 指针变量 4. 解引用 4.1 *解引用 4.2 []解引用 4.3 ->解引用 5. 指针变量的大小 5.1 结论 6. 指针运算 7. void* 指针 8. const修饰指针 8.1 const修饰变量 8.2 const修饰指针变量 8.3 结论 9. 野指针 9.1 为什么会出现野指…...

PHP+vue+mysql校园学生社团管理系统574cc
运行环境:phpstudy/wamp/xammp等 开发语言:php 后端框架:Thinkphp 前端框架:vue.js 服务器:apache 数据库:mysql 数据库工具:Navicat/phpmyadmin 前台功能: 首页:展示社团信息和活动…...
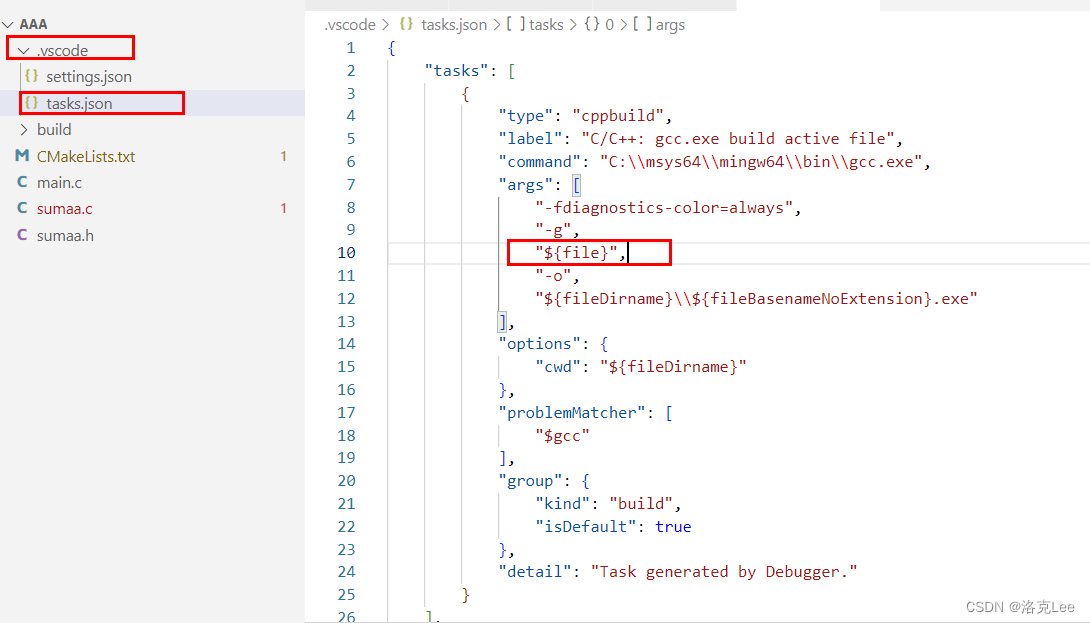
VS Code中主程序C文件引用了另一个.h头文件,编译时报错找不到函数
目录 一、问题描述二、问题原因三、解决方法四、扩展五、通过CMake进行配置 一、问题描述 VS Code中主程序C文件引用了另一个.h头文件,编译时报错找不到函数 主程序 main.c #include <stdio.h> #include "sumaa.h"int main(int, char**){printf(&q…...

边缘计算:重塑数字世界的未来
引言 随着物联网(IoT)设备的激增和5G网络的普及,我们正站在一个计算模式的新纪元门槛上——边缘计算。这一技术范式将数据处理和分析推向网络的边缘,即设备或终端,为实时性要求较高的应用提供了前所未有的可能性。 目…...

2024 前端面试题 附录3
这里记录的是昨天和今天原篇的知识点补充 原篇地址: 2024 前端面试题(GPT回答 示例代码 解释)No.41 - No.60 2024 前端面试题(GPT回答 示例代码 解释)No.61 - No.100 2024 前端面试题(GPT回答 示例代…...

[Vue warn]: Duplicate keys detected: ‘1‘. This may cause an update error.
[Vue warn]: Duplicate keys detected: ‘1‘. This may cause an update error.——> Vue报错,key关键字不唯一: 解决办法:修改一下重复的id值!!!...

Docker-Learn(二)保存、导入、使用Docker镜像
1.保存镜像 根据上一节内容,将创建好镜像进行保存,需要退出当前的已经在运行的docer命令行中断里面,可以通过在终端里面输入指令exit或者按下键盘上的 ctrlD建退出: 回到自己的终端里面,输入指令: docker…...

第三百一十五回
文章目录 1. 概念介绍2. 基本用法3. 补充用法4. 内容总结 我们在上一章回中介绍了"再谈ListView中的分隔线",本章回中将介绍showMenu的用法.闲话休提,让我们一起Talk Flutter吧。 1. 概念介绍 我们在第一百六十三回中介绍了showMenu相关的内容…...
区块链(一): 以太坊基础知识
目录 什么是区块链?什么是以太坊?什么是加密货币?以太坊与比特币有什么不同?以太坊能做什么?什么是智能合约?以太坊社区以太坊白皮书 什么是区块链? 区块链是一个交易数据库,在网络…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...

FOPLP vs CoWoS
以下是 FOPLP(Fan-out panel-level packaging 扇出型面板级封装)与 CoWoS(Chip on Wafer on Substrate)两种先进封装技术的详细对比分析,涵盖技术原理、性能、成本、应用场景及市场趋势等维度: 一、技术原…...
