2024牛客寒假算法基础集训营2-c Tokitsukaze and Min-Max XOR
来源
题目
Tokitsukaze 有一个长度为 n 的序列 a1,a2,…,an和一个整数 k。
她想知道有多少种序列 b1,b2,…,bm满足:
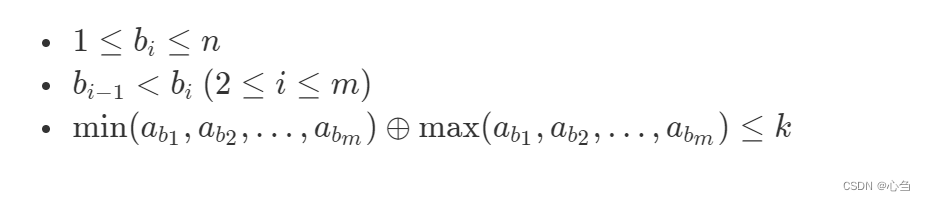
其中 ⊕\oplus⊕ 为按位异或,具体参见 百度百科:异或
答案可能很大,请输出 mod1e9+7 后的结果。
输入描述:
第一行包含一个整数 T(1≤T≤2e5),表示 T 组测试数据。对于每组测试数据:第一行包含两个整数 n, k (1≤n≤2⋅e5; 0≤k≤1e9)。第二行包含 nnn 个整数 a1,a2,…,an (0≤ai≤1e9)。
输出描述:
对于每组测试数据,输出一个整数,表示答案 mod1e9+7 后的结果。
输入
3 3 2 1 3 2 5 3 1 3 5 2 4 5 0 0 0 0 0 0
输出
6 10 31
思路
容易知道 b1,…,bm 实际上是 a 的一个子序列,并且由于我们只关注子序列中的最大值和最小值,因此可以先对 a 从小到大排序,再选择子序列。接着对子序列中的最大值进行分类,可以分成 n 类。即从左到右依次枚举 ai 作为子序列中的最大值,那么最小值就会在 aj, j∈[0,i] 中选。当满足 ai⊕aj≤k,那么以 ai 为最大值,aj 为最小值的子序列的数量就是 2的max{0,i−j−1}次方,特别的当 i=j 时答案为 1。
暴力的做法就是逐个枚举 aj 判断是否满足条件,时间复杂度是 O() 的。由于涉及到异或运算所以尝试能不能用 trie 来维护 aj 的信息。如果 aj 满足条件,那么对答案的贡献是
,也就是
,因此在把 aj 按位插入 trie 中时,同时在对应节点加上
。
枚举到 ai 时,此时已经往 trie 中插入了 a0∼ai−1,枚举 ai 的每一位,用 xi 和 ki 分别表示 ai 和 k 在二进制下第 i 位上的值,s表示累加和。
1.当xi=1,ki=1时,显然另一数aj这一位是1的情况都是可以的,因为 1⊕1=0<1,所以s加上这一位为1的节点的值了,下一步走0节点。
2.当xi=0,ki=1时,同理s加上0节点的值,下一步走1节点.
3.当xi=1,ki=0时,0节点必然不成立,因为 1⊕0=1>0,下一步走1节点。
4.当xi=0,ki=0时,同理,1节点必然不成立,下一步走0节点。
最后以 ai 为最大值的子序列的数量就是。
代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
//#define double long double
typedef long long ll;
const int N = 2e5+100;
const int mod = 1e9+7;
const int INF = 0x3f3f3f3f3f3f3f;
//ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);int a[N];
int to[N * 35][2];
int val[N * 35];
int tot = 0;void insert(int x,int c) {int p = 0;for (int i = 30; i >= 0; i--) {int v = (x >> i & 1);if (!to[p][v]) {to[p][v] = ++tot;}val[to[p][v]] = (val[to[p][v]] + c) % mod;p = to[p][v];}
}int sum(int x,int k) {int p = 0, res = 0;for (int i = 30; i >= 0; i--) {int vx = (x >> i & 1), vk = (k >> i & 1);if (vk == 1 && vx == 1) {res = (res + val[to[p][1]]) % mod;p = to[p][0];} else if (vk == 1 && vx == 0) {res = (res + val[to[p][0]]) % mod;p = to[p][1];} else {p = to[p][vx];}if (!p) break;if (!i) res = (res + val[p]) % mod;}return res;
}int ksm(int x,int n) {int res = 1;while (n) {if (n & 1) res = res * x % mod;x = x * x % mod;n >>= 1;}return res;
}void solve() {int n,k;cin >> n >> k;for(int i=0;i<n;i++)cin>>a[i];sort(a,a+n);tot = 0;for (int i = 0; i <= n * 32; i++) {val[i] = 0;to[i][0] = to[i][1] = 0;}int ans = 0;for (int i = 1; i <= n; i++) {ans = (ans + 1 + ksm(2,i - 1) * sum(a[i - 1],k) % mod) % mod;insert(a[i - 1],ksm(ksm(2,i),mod - 2));}cout << ans << '\n';
}signed main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--)solve();return 0;
}相关文章:
2024牛客寒假算法基础集训营2-c Tokitsukaze and Min-Max XOR
来源 题目 Tokitsukaze 有一个长度为 n 的序列 a1,a2,…,an和一个整数 k。 她想知道有多少种序列 b1,b2,…,bm满足: 其中 ⊕\oplus⊕ 为按位异或,具体参见 百度百科:异或 答案可能很大,请输出 mod1e97 后的结果。 输入描述…...

C语言:指针的基础详解
目录 1. 内存 2. 取地址& 3. 指针变量 4. 解引用 4.1 *解引用 4.2 []解引用 4.3 ->解引用 5. 指针变量的大小 5.1 结论 6. 指针运算 7. void* 指针 8. const修饰指针 8.1 const修饰变量 8.2 const修饰指针变量 8.3 结论 9. 野指针 9.1 为什么会出现野指…...

PHP+vue+mysql校园学生社团管理系统574cc
运行环境:phpstudy/wamp/xammp等 开发语言:php 后端框架:Thinkphp 前端框架:vue.js 服务器:apache 数据库:mysql 数据库工具:Navicat/phpmyadmin 前台功能: 首页:展示社团信息和活动…...
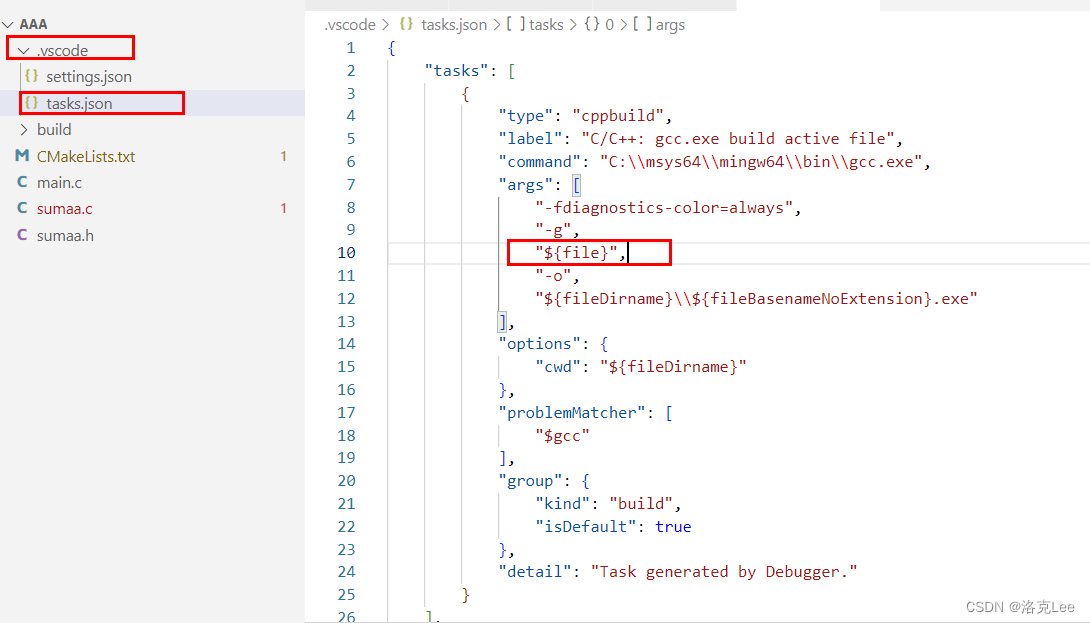
VS Code中主程序C文件引用了另一个.h头文件,编译时报错找不到函数
目录 一、问题描述二、问题原因三、解决方法四、扩展五、通过CMake进行配置 一、问题描述 VS Code中主程序C文件引用了另一个.h头文件,编译时报错找不到函数 主程序 main.c #include <stdio.h> #include "sumaa.h"int main(int, char**){printf(&q…...

边缘计算:重塑数字世界的未来
引言 随着物联网(IoT)设备的激增和5G网络的普及,我们正站在一个计算模式的新纪元门槛上——边缘计算。这一技术范式将数据处理和分析推向网络的边缘,即设备或终端,为实时性要求较高的应用提供了前所未有的可能性。 目…...

2024 前端面试题 附录3
这里记录的是昨天和今天原篇的知识点补充 原篇地址: 2024 前端面试题(GPT回答 示例代码 解释)No.41 - No.60 2024 前端面试题(GPT回答 示例代码 解释)No.61 - No.100 2024 前端面试题(GPT回答 示例代…...

[Vue warn]: Duplicate keys detected: ‘1‘. This may cause an update error.
[Vue warn]: Duplicate keys detected: ‘1‘. This may cause an update error.——> Vue报错,key关键字不唯一: 解决办法:修改一下重复的id值!!!...

Docker-Learn(二)保存、导入、使用Docker镜像
1.保存镜像 根据上一节内容,将创建好镜像进行保存,需要退出当前的已经在运行的docer命令行中断里面,可以通过在终端里面输入指令exit或者按下键盘上的 ctrlD建退出: 回到自己的终端里面,输入指令: docker…...

第三百一十五回
文章目录 1. 概念介绍2. 基本用法3. 补充用法4. 内容总结 我们在上一章回中介绍了"再谈ListView中的分隔线",本章回中将介绍showMenu的用法.闲话休提,让我们一起Talk Flutter吧。 1. 概念介绍 我们在第一百六十三回中介绍了showMenu相关的内容…...
区块链(一): 以太坊基础知识
目录 什么是区块链?什么是以太坊?什么是加密货币?以太坊与比特币有什么不同?以太坊能做什么?什么是智能合约?以太坊社区以太坊白皮书 什么是区块链? 区块链是一个交易数据库,在网络…...
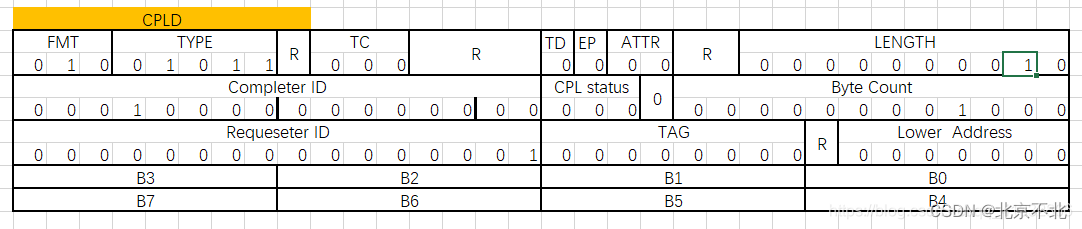
高级FPGA开发之基础协议PCIe
基础协议之PCIe部分 一、TLP包的包头 在PCIe的系统中,tlp包的包头的结构有许多部分是相似的,通过掌握这些常规的包头,能帮助理解在PCIe总线上各个设备之间如何进行数据的收发。 通用的字段 通用字段作用Fmt决定了包头是3DW还是3DWÿ…...
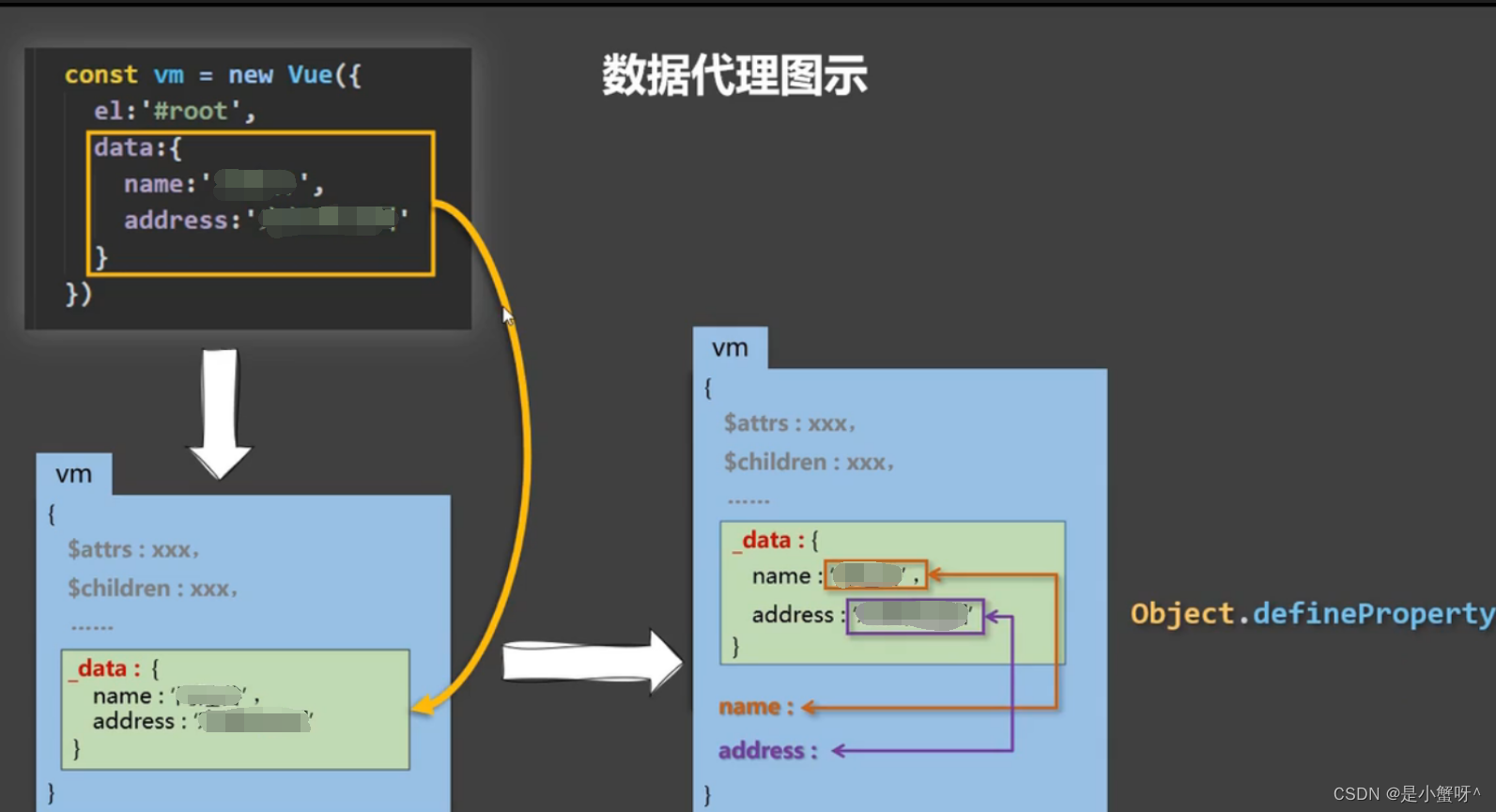
Vue核心基础1:数据代理
1 回顾Object.defineProperty方法 let str hello const person {name: 张三,age: 18 } Object.defineProperty(person, sex, {// value: 男,// enumerable: true, // 控制属性是否可以枚举,默认值是false// writable: true, // 控制属性是否可以被修改࿰…...
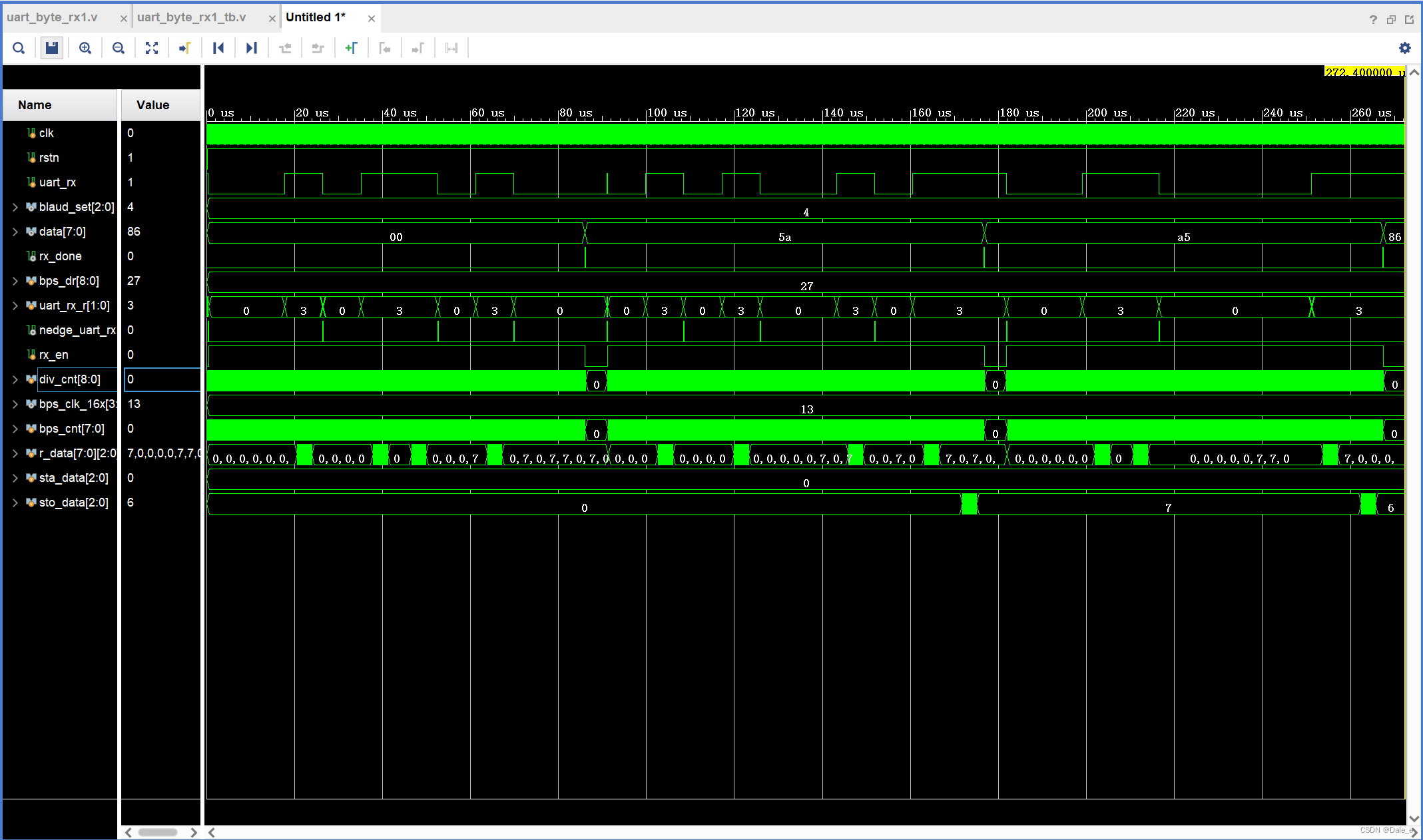
12 ABC串口接收原理与思路
1. 串口接收原理 基本原理:通过数据起始位判断要是否要开始接收的数据,通过采样的方式确定每一位数据是0还是1。 如何判断数据起始位到来:通过边沿检测电路检测起始信号的下降沿 如何采样:一位数据采多次,统计得到高…...
leetcode(二分查找)34.在排序数组中查找元素的第一个和最后一个位置(C++详细解释)DAY11
文章目录 1.题目示例提示 2.解答思路3.实现代码结果 4.总结 1.题目 给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。 如果数组中不存在目标值 target,返回 [-1, -1]。 你必须设计…...

算法刷题框架
前言:最近积累了一些算法题量,正在刷东神的算法笔记,监督自己记录下读后启发,顺便帮助道友们阅读 数据结构 这一部分老生常谈,数据的存储方式只有顺序存储和链式存储。 最基本的数组和链表对应这两者,栈…...
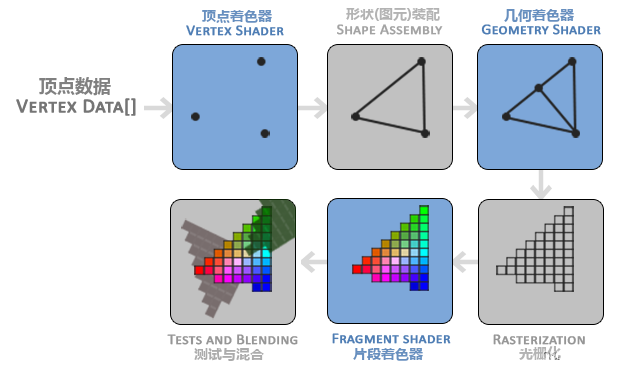
跟着cherno手搓游戏引擎【24】开启2D引擎前的项目总结(包括前置知识汇总)
前置技术: c动态链接和静态链接: 隐藏的细节:编译与链接_哔哩哔哩_bilibili 【底层】动态链接库(dll)是如何工作的?_哔哩哔哩_bilibili 预编译,编译,汇编,链接 预编译头文件: 为…...

石子合并+环形石子合并+能量项链+凸多边形的划分——区间DP
一、石子合并 (经典例题) 设有 N 堆石子排成一排,其编号为 1,2,3,…,N。 每堆石子有一定的质量,可以用一个整数来描述,现在要将这 N 堆石子合并成为一堆。 每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,…...
IMX6ULL移植U-Boot 2022.04
目录 目录 1.编译环境以及uboot版本 2.默认编译测试 3.uboot中新增自己的开发板 3.编译测试 4.烧录测试 5.patch文件 1.编译环境以及uboot版本 宿主机Debian12u-boot版本lf_v2022.04 ; git 连接GitHub - nxp-imx/uboot-imx: i.MX U-Boot交叉编译工具gcc-arm-10.3-2021.0…...

ES实战-高级聚合
多桶型聚合 1.词条聚合–terms 2.范围聚合–range 3,直方图聚合–histogram/日期直方图 4.嵌套聚合 5.地理距离聚合 include(包含)exclude(不包含) GET /get-together/_search?pretty {"size": 0,"aggs": {"tags": {"terms": {"…...

网络安全产品之认识蜜罐
文章目录 一、什么是蜜罐二、蜜罐的主要类型三、蜜罐的主要功能四、蜜罐的主要组成及核心技术五、蜜罐的优缺点六、蜜罐如何与其他安全工具协同工作?七、什么是“蜜网”?与蜜罐的联系和区别是什么? 蜜罐的概念首次由Clifford Stoll在其1988年…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
