石子合并+环形石子合并+能量项链+凸多边形的划分——区间DP
一、石子合并 (经典例题)
设有 N 堆石子排成一排,其编号为 1,2,3,…,N。
每堆石子有一定的质量,可以用一个整数来描述,现在要将这 N 堆石子合并成为一堆。
每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的石子将和新堆相邻,合并时由于选择的顺序不同,合并的总代价也不相同。
例如有 4 堆石子分别为 1 3 5 2, 我们可以先合并 1、2 堆,代价为 4,得到 4 5 2, 又合并 1、2 堆,代价为 9,得到 9 2 ,再合并得到 11,总代价为 4+9+11=24;
如果第二步是先合并 2、3 堆,则代价为 7,得到 4 7,最后一次合并代价为 11,总代价为 4+7+11=22。
问题是:找出一种合理的方法,使总的代价最小,输出最小代价。
输入
第一行一个数 N 表示石子的堆数 N (1 ≤ N ≤ 300)。
第二行 N 个数,表示每堆石子的质量(均不超过 1000)。
输出
输出一个整数,表示最小代价。
Input
4
1 3 5 2
Output
22
解析:
用一个状态表示一个区间,f[i][j] 表示将第 i 堆石子到第 j 堆石子合并成一堆石子的合并方式的集合。
状态转移:
例如,将 区间 [i,j] 分为 [i,k] 和 [k+1,j] ,枚举 k 在区间[i,j]的位置就能找到最小代价使得 合并这两个区间的代价最小,即 f[i][k]+f[k+1,j] 的值最小,再加上一个第 i 堆到第 j 堆的总重量即可。
因为在计算状态的时候,得保证在这个状态之前的状态已经计算完毕,所以可以采用循环区间长度从小到大的方式,进行计算。
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define ios ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
int gcd(int a,int b) { return b? gcd(b,a%b) : a; }
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const int N=310;
int n;
int s[N];
int f[N][N];
void solve()
{cin>>n;for (int i=1;i<=n;i++) cin>>s[i];for (int i=1;i<=n;i++) s[i] +=s[i-1];for (int len=1;len<=n;len++)for (int i=1;i+len-1<=n;i++){int l=i,r=i+len-1;if(len!=1) f[l][r]=2e9; //因为当len=1时,只有一堆石子,不需要合并,代价为0for (int k=l;k<r;k++)f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);}cout<<f[1][n];
}
signed main()
{ios;int T=1;//cin>>T;while (T--) solve();return 0;
}
二、 环形石子合并 (加个环)
将 n 堆石子绕圆形操场排放,现要将石子有序地合并成一堆。
规定每次只能选相邻的两堆合并成新的一堆,并将新的一堆的石子数记做该次合并的得分。
请编写一个程序,读入堆数 n 及每堆的石子数,并进行如下计算:
选择一种合并石子的方案,使得做 n−1 次合并得分总和最大。
选择一种合并石子的方案,使得做 n−1 次合并得分总和最小。
输入
第一行包含整数 n (1 ≤ n ≤ 200),表示共有 n 堆石子。
第二行包含 n 个整数,分别表示每堆石子的数量。
输出
共两行,第一行为合并得分总和最小值,第二行为合并得分总和最大值。
Input
4
4 5 9 4
Output
43
54
解析:
与上一题的石子合并的想法基本相似,不同的是这道题的石堆的摆放方式是环式的。
在上道题的基础上,将这个环断开,变成一条链,枚举每个断点。
不过直接枚举的话,时间复杂度是 n^4,超时了。
我们可以将数组读入,再将数组复制一遍,再接到这个数组上。
这样时间复杂度就降下来了,时间复杂度在 n^3。
注意:在做这种环式的题,就可以多想一想这样的方法
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define ios ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
int gcd(int a,int b) { return b? gcd(b,a%b) : a; }
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const int N=410;
int n;
int a[N],s[N];
int f[N][N],g[N][N];
void solve()
{cin>>n;for (int i=1;i<=n;i++) cin>>a[i],a[i+n]=a[i];for (int i=1;i<=2*n;i++) s[i]=s[i-1]+a[i];for (int len=1;len<=n;len++) //一层循环枚举区间长度for (int i=1;i+len-1<=2*n;i++) //二层循环枚举区间的左右端点{int l=i,r=i+len-1;if (len!=1) f[l][r]=2e9,g[l][r]=-2e9;for (int k=l;k<r;k++) //状态转移{f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);g[l][r]=max(g[l][r],g[l][k]+g[k+1][r]+s[r]-s[l-1]);}}int minx=2e9,maxx=-2e9; //找到最小值,最大值for (int i=1;i<=n;i++) {minx=min(minx,f[i][i+n-1]);maxx=max(maxx,g[i][i+n-1]);}cout<<minx<<endl<<maxx<<endl;
}
signed main()
{ios;int T=1;//cin>>T;while (T--) solve();return 0;
}三、能量项链 (跟上个题一样)
在 Mars 星球上,每个 Mars 人都随身佩带着一串能量项链,在项链上有 N 颗能量珠。
能量珠是一颗有头标记与尾标记的珠子,这些标记对应着某个正整数。
并且,对于相邻的两颗珠子,前一颗珠子的尾标记一定等于后一颗珠子的头标记。
因为只有这样,通过吸盘(吸盘是 Mars 人吸收能量的一种器官)的作用,这两颗珠子才能聚合成一颗珠子,同时释放出可以被吸盘吸收的能量。
如果前一颗能量珠的头标记为 m,尾标记为 r,后一颗能量珠的头标记为 r,尾标记为 n,则聚合后释放的能量为 m×r×n(Mars 单位),新产生的珠子的头标记为 m,尾标记为 n。
需要时,Mars 人就用吸盘夹住相邻的两颗珠子,通过聚合得到能量,直到项链上只剩下一颗珠子为止。
显然,不同的聚合顺序得到的总能量是不同的,请你设计一个聚合顺序,使一串项链释放出的总能量最大。
例如:设 N=4,4 颗珠子的头标记与尾标记依次为 (2,3)(3,5)(5,10)(10,2)。
我们用记号 ⊕ 表示两颗珠子的聚合操作,(j⊕k) 表示第 j,k 两颗珠子聚合后所释放的能量。则
第 4、1 两颗珠子聚合后释放的能量为:(4⊕1)=10×2×3=60。
这一串项链可以得到最优值的一个聚合顺序所释放的总能量为 ((4⊕1)⊕2)⊕3)=10×2×3+10×3×5+10×5×10=710。
输入
输入的第一行是一个正整数 N (4 ≤ N ≤ 100),表示项链上珠子的个数。
第二行是 N 个用空格隔开的正整数,所有的数均不超过 1000,第 i 个数为第 i 颗珠子的头标记,当 i<N 时,第 i 颗珠子的尾标记应该等于第 i+1 颗珠子的头标记,第 N 颗珠子的尾标记应该等于第 1 颗珠子的头标记。
至于珠子的顺序,你可以这样确定:将项链放到桌面上,不要出现交叉,随意指定第一颗珠子,然后按顺时针方向确定其他珠子的顺序。
输出
输出只有一行,是一个正整数 E (1 ≤ E ≤ 2e9),为一个最优聚合顺序所释放的总能量。
Input
4
2 3 5 10
Output
710
解析:
跟上一题一样,纯套路。
//代码一:开个结构体存储头和尾,相当于一个点,就跟上道题一模一样了
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define ios ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
int gcd(int a,int b) { return b? gcd(b,a%b) : a; }
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const int N=400;
struct node
{int x,y;
}str[N];
int n;
int a[N];
int f[N][N];
void solve()
{cin>>n;for (int i=1;i<=n;i++) cin>>a[i];for (int i=1;i<=n;i++){if (i==1) str[i]={a[n],a[i]};else str[i]={a[i-1],a[i]};str[i+n]=str[i];}for (int len=1;len<=n;len++)for (int i=1;i+len-1<=2*n;i++){int l=i,r=i+len-1;if (len!=1) f[l][r]=-2e9;for (int k=l;k<r;k++){f[l][r]=max(f[l][r],f[l][k]+f[k+1][r]+str[l].x*str[k].y*str[r].y); //左区间左端点的头*左区间右端点的尾*右区间右端点的尾}}int ans=-2e9;for (int i=1;i<=n;i++) ans=max(ans,f[i][i+n-1]);cout<<ans;
}
signed main()
{ios;int T=1;//cin>>T; while (T--) solve();return 0;
}//代码二
//划分方式:f(l,r)=f(l,k)+f(k,r)+a[l]*a[k]*a[r]
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define ios ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
int gcd(int a,int b) { return b? gcd(b,a%b) : a; }
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const int N=400;
int n;
int a[N];
int f[N][N];
void solve()
{cin>>n;for (int i=1;i<=n;i++) cin>>a[i],a[i+n]=a[i];for (int len=3;len<=n+1;len++) //至少 3 个点for (int i=1;i+len-1<=2*n;i++){int l=i,r=i+len-1;f[l][r]=-2e9;for (int k=l;k<r;k++){f[l][r]=max(f[l][r],f[l][k]+f[k][r]+a[l]*a[k]*a[r]); }}int ans=-2e9;for (int i=1;i<=n;i++) ans=max(ans,f[i][i+n]); //查找区间长度为 n+1 的cout<<ans;
}
signed main()
{ios;int T=1;//cin>>T; while (T--) solve();return 0;
}四、凸多边形的划分
给定一个具有 N 个顶点的凸多边形,将顶点从 1 至 N 标号,每个顶点的权值都是一个正整数。
将这个凸多边形划分成 N−2 个互不相交的三角形,对于每个三角形,其三个顶点的权值相乘都可得到一个权值乘积,试求所有三角形的顶点权值乘积之和至少为多少。
输入
第一行包含整数 N (N ≤ 50),表示顶点数量。
第二行包含 N 个整数,依次为顶点 1 至顶点 N 的权值。
输出
输出仅一行,为所有三角形的顶点权值乘积之和的最小值。
数据保证所有顶点的权值都小于 1e9
Input
5
121 122 123 245 231
Output
12214884
解析:

f[l][r] 表示 所有 由(l,l+1)(l+1,l+2)……(r-1,r)(r,l)这些边组成的多边形 划分成三角形的方案的集合。
跟上道题的划分是一样的,不过不需要破环成链,因为枚举哪一条边都是一样的。
这里的运算数据太大,需要高精度运算。
//代码一:没有加高精度的代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define ios ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
int gcd(int a,int b) { return b? gcd(b,a%b) : a; }
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const int N=110;
int n;
int w[N];
int f[N][N];
int INF=1e18;
void solve()
{cin>>n;for (int i=1;i<=n;i++) cin>>w[i];for (int len=3;len<=n;len++)for (int i=1;i+len-1<=n;i++){int l=i,r=i+len-1;f[l][r]=INF;for (int k=l;k<r;k++){f[l][r]=min(f[l][r],f[l][k]+f[k][r]+w[l]*w[k]*w[r]);}}cout<<f[1][n];
}
signed main()
{ios;int T=1;//cin>>T; while (T--) solve();return 0;
}//代码二:加了高精度的代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define ios ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
int gcd(int a,int b) { return b? gcd(b,a%b) : a; }
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const int N=55,M=35,INF=1e9;
int n;
int w[N];
int f[N][N][M];
int c[M];
void add(int a[],int b[])
{memset(c,0,sizeof c);int t=0;for (int i=0;i<M;i++){t +=a[i]+b[i];c[i]=t%10;t /=10;}memcpy(a,c,sizeof c);
}
void mul(int a[],int b)
{memset(c,0,sizeof c);int t=0;for (int i=0;i<M;i++){t +=a[i]*b;c[i]=t%10;t /=10;}memcpy(a,c,sizeof c);
}
int cmp(int a[],int b[])
{for (int i=M-1;i>=0;i--){if (a[i]>b[i]) return 1;else if (a[i]<b[i]) return -1;}return 0;
}
void print(int a[])
{int k=M-1;while (k&&!a[k]) k--;while (k>=0) cout<<a[k--];cout<<endl;
}
int temp[M];
void solve()
{cin>>n;for (int i=1;i<=n;i++) cin>>w[i];for (int len=3;len<=n;len++)for (int i=1;i+len-1<=n;i++){int l=i,r=i+len-1;f[l][r][M-1]=1;for (int k=l+1;k<r;k++){memset(temp,0,sizeof temp);temp[0]=w[l];mul(temp,w[k]);mul(temp,w[r]);add(temp,f[l][k]);add(temp,f[k][r]);if (cmp(f[l][r],temp)>0) memcpy(f[l][r],temp,sizeof temp);}}print(f[1][n]);
}
signed main()
{ios;int T=1;//cin>>T; while (T--) solve();return 0;
}
相关文章:

石子合并+环形石子合并+能量项链+凸多边形的划分——区间DP
一、石子合并 (经典例题) 设有 N 堆石子排成一排,其编号为 1,2,3,…,N。 每堆石子有一定的质量,可以用一个整数来描述,现在要将这 N 堆石子合并成为一堆。 每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,…...
IMX6ULL移植U-Boot 2022.04
目录 目录 1.编译环境以及uboot版本 2.默认编译测试 3.uboot中新增自己的开发板 3.编译测试 4.烧录测试 5.patch文件 1.编译环境以及uboot版本 宿主机Debian12u-boot版本lf_v2022.04 ; git 连接GitHub - nxp-imx/uboot-imx: i.MX U-Boot交叉编译工具gcc-arm-10.3-2021.0…...

ES实战-高级聚合
多桶型聚合 1.词条聚合–terms 2.范围聚合–range 3,直方图聚合–histogram/日期直方图 4.嵌套聚合 5.地理距离聚合 include(包含)exclude(不包含) GET /get-together/_search?pretty {"size": 0,"aggs": {"tags": {"terms": {"…...

网络安全产品之认识蜜罐
文章目录 一、什么是蜜罐二、蜜罐的主要类型三、蜜罐的主要功能四、蜜罐的主要组成及核心技术五、蜜罐的优缺点六、蜜罐如何与其他安全工具协同工作?七、什么是“蜜网”?与蜜罐的联系和区别是什么? 蜜罐的概念首次由Clifford Stoll在其1988年…...

推荐《架构探险:从零开始写Java Web框架》
版权声明 本文原创作者:谷哥的小弟作者博客地址:http://blog.csdn.net/lfdfhl 春节读了《架构探险:从零开始写Java Web框架》,一本大概10年前的好书。 本书的作者是阿里巴巴架构师黄勇。黄勇对分布式服务架构与大数据技术有深入…...

Go教程-Go语言简介
这篇文章我们来聊聊Go语言。 Go语言发展历史 以下是Go语言发展的几个里程碑节点: Go一开始是Google内部的一个项目,由三位大佬Rob Pike、Robert Griesemer、Ken Thompson早2007年发起。在2009年11月,Go语言正式对外开源。在2010年…...

React + SpringBoot + Minio实现文件的预览
思路:后端提供接口,从minio获取文件的预览链接,返回给前端,前端使用组件进行渲染展示 这里我从minio获取文件预览地址用到了一个最近刚开源的项目,挺好用的,大伙可以试试,用法也很简单 官网&am…...

心法利器[107] onnx和tensorRT的bert加速方案记录
心法利器 本栏目主要和大家一起讨论近期自己学习的心得和体会,与大家一起成长。具体介绍:仓颉专项:飞机大炮我都会,利器心法我还有。 2023年新一版的文章合集已经发布,获取方式看这里:又添十万字-CS的陋室2…...
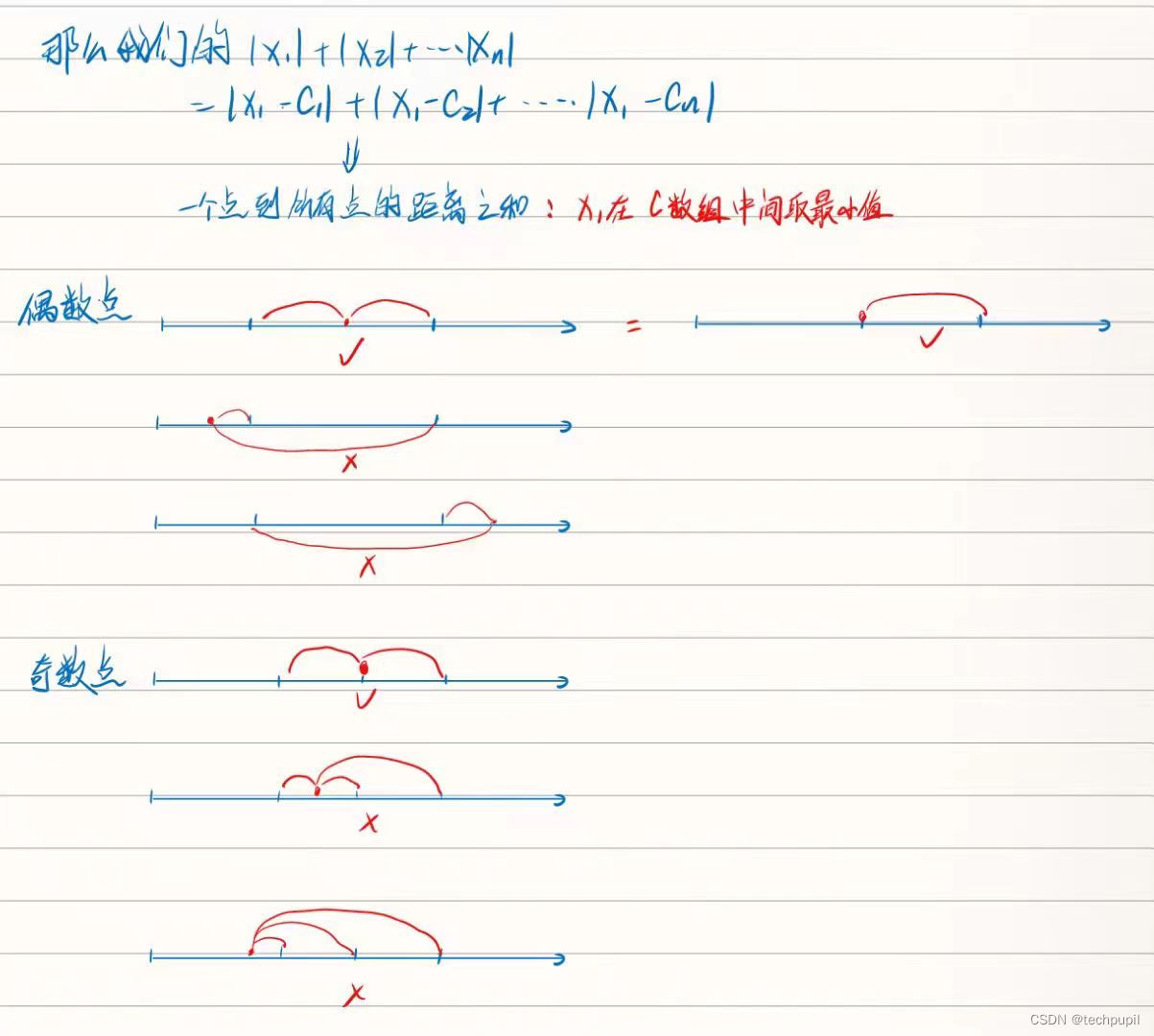
AcWing 122 糖果传递(贪心)
[题目概述] 有 n 个小朋友坐成一圈,每人有 a[i] 个糖果。 每人只能给左右两人传递糖果。 每人每次传递一个糖果代价为 1。 求使所有人获得均等糖果的最小代价。 输入格式 第一行输入一个正整数 n,表示小朋友的个数。 接下来 n 行,每行一个…...
unity的重中之重:组件
检查器(Hierarchy)面板中的所有东西都是组件。日后多数工作都是和组件打交道,包括调参、自定义脚本组件。 文章目录 12 游戏的灵魂,脚本组件13 玩转脚本组件14 尽职的一生,了解组件的生命周期15 不能插队!…...

Linux释放内存
free -m是Linux上查看内存的指令,其中-m是以兆(MB)为单位,如果不加则以KB为单位。 如下图表示,(total)总物理内存是809MB,(used)已使用167MB,&…...

Python算法题集_翻转二叉树
Python算法题集_翻转二叉树 题226:翻转二叉树1. 示例说明2. 题目解析- 题意分解- 优化思路- 测量工具 3. 代码展开1) 标准求解【DFS递归】2) 改进版一【BFS迭代,节点循环】3) 改进版二【BFS迭代,列表循环】 4. 最优算法 本文为Python算法题集…...
Git快速掌握,通俗易懂
Git分布式版本控制工具 介绍 Git是一个开源的分布式版本控制系统,用于敏捷高效地处理任何或小或大的项目。Git是由Linus Torvalds为了帮助管理Linux内核开发而开发的一个开放源码的版本控制软件。Git可以帮助开发者们管理代码的版本,避免代码冲突&#…...
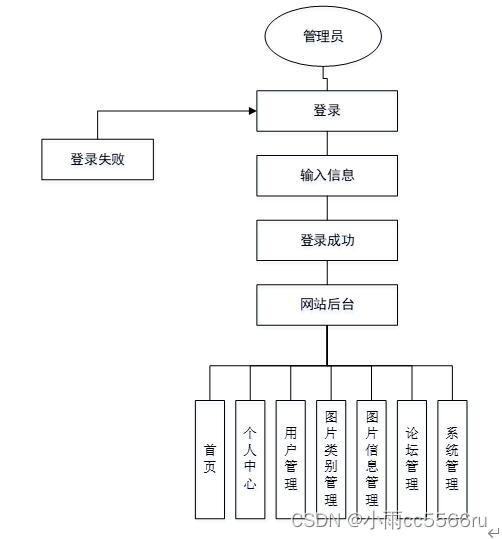
PHP毕业设计图片分享网站76t17
图片分享网站主要是为了提高工作人员的工作效率和更方便快捷的满足用户,更好存储所有数据信息及快速方便的检索功能,对系统的各个模块是通过许多今天的发达系统做出合理的分析来确定考虑用户的可操作性,遵循开发的系统优化的原则,…...

代码随想录 Leetcode45. 跳跃游戏 II
题目: 代码(首刷看解析 2024年2月15日): class Solution { public:int jump(vector<int>& nums) {if (nums.size() 1) return 0;int res 0;int curDistance 0;int nextDistance 0;for (int i 0; i < nums.size(); i) {nex…...

【C语言】socketpair 的系统调用
一、 Linux 内核 4.19socketpair 的系统调用 SYSCALL_DEFINE4(socketpair, int, family, int, type, int, protocol,int __user *, usockvec) {return __sys_socketpair(family, type, protocol, usockvec); } 这段代码定义了一个名为 socketpair 的系统调用。系统调用是操作…...

【论文精读】BERT
摘要 以往的预训练语言表示应用于下游任务时的策略有基于特征和微调两种。其中基于特征的方法如ELMo使用基于上下文的预训练词嵌入拼接特定于任务的架构;基于微调的方法如GPT使用未标记的文本进行预训练,并针对有监督的下游任务进行微调。 但上述两种策略…...
 - A、B、C、D、E)
Codeforces Round 925 (Div. 3) - A、B、C、D、E
文章目录 前言A. Recovering a Small StringB. Make EqualC. Make Equal AgainD. Divisible PairsE. Anna and the Valentines Day Gift 前言 本篇博客是Codeforces Round 925周赛的A、B、C、D、E五题的题解 A. Recovering a Small String 可以通过sum的大小分为三种情况&#…...

快速部署MES源码/万界星空科技开源MES
什么是开源MES软件? 开源MES软件是指源代码可以免费获取、修改和分发的MES软件。与传统的商业MES软件相比,开源MES软件具有更高的灵活性和可定制性。企业可以根据自身的需求对软件进行定制化开发,满足不同生产环境下的特定需求。 开源MES软件…...
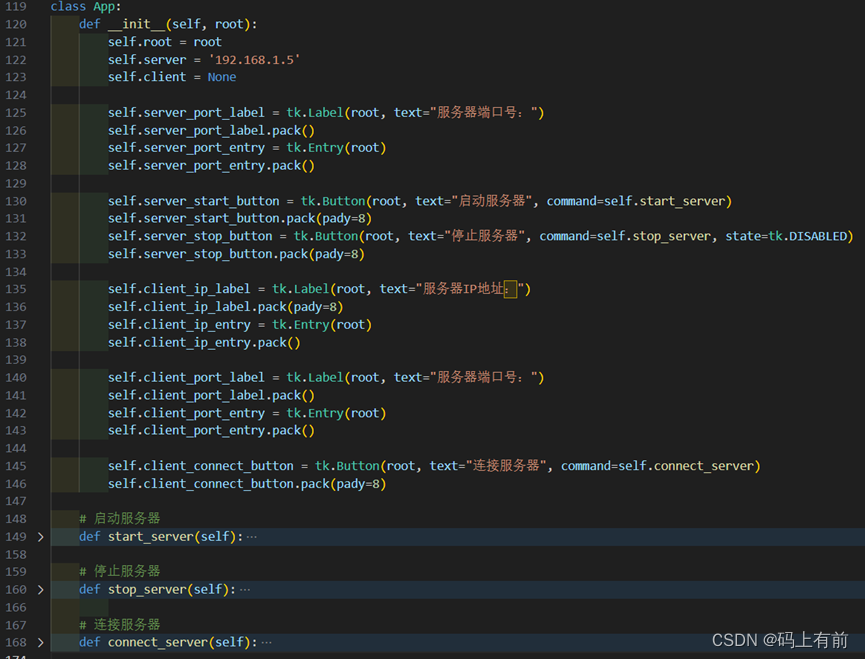
【Python网络编程之TCP三次握手】
🚀 作者 :“码上有前” 🚀 文章简介 :Python开发技术 🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬 Python网络编程之[TCP三次握手] 代码见资源,效果图如下一、实验要求二、协议原理2.…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
